Слайд 1Базы данных
Реляционная модель данных
Слайд 2Основные определения
Домен – множество возможных значений некоторой величины из предметной
области.
Примеры доменов
Фамилия = {Иванов, Петров, Сидоров}
Дисциплина = {БД, СПО,
ПЯВУ}
D1 = {2,4} D2 = {1,3,5}
Декартово произведение множеств – множество всевозможных пар элементов из D1 и D2
D1 × D2 = {(2,1), (2,3) , (2,5) , (4,1) , (4,3) , (4,5)}
Слайд 3Основные определения
Отношение – любое подмножество из декартова произведения доменов.
Не формально:
отношение (relationship) – зависимость одних данных от других
Например,
R = {(2,1),
(4,1)}
D1 × D2 = {(2,1), (2,3) , (2,5) , (4,1) , (4,3) , (4,5)}
Слайд 4Характеристики отношения
Отношение моделирует реальную ситуацию, т.е. для каждого элемента из
R можно утверждать, что он соответствуют действительности
Кортеж = Строка =
n-ка
Атрибут - вхождение домена в отношение
Степень отношения – количество атрибутов
Кардинальность – количество кортежей
Схема отношения – перечень имен атрибутов с указанием соответствующих доменов
Слайд 5Свойства отношения
В отношении нет двух одинаковых кортежей
Порядок следования кортежей –
произвольный
Атрибуты имеют уникальные имена
Пример атрибутов из одного домена
R =
студента : Фамилия, Год рождения : Год, Год поступления : Год>
Слайд 6Свойства отношения
Если атрибуты из одного домена, то они называются θ-сравнимыми,
где θ - множество операций сравнения для заданного домена. Например,
место рождения и место жительства – сравнимы, место рождения и год рождения не сравнимы (разные домены).
Для домена «Год» θ = {=, <>, >, <, >=, <=}
Для домена «Место» θ = {=, <>}
Эквивалентные схемы – одинаковая степень и одинаковый порядок следования атрибутов
Слайд 7Реляционные ключи
Реляционная модель данных – совокупность взаимосвязанных отношений. Для поддержки
иерархических связей предназначены ключи.
Суперключ – атрибут или множество атрибутов,
однозначно определяющие кортеж данного отношения.
Потенциальный ключ – суперключ, который не содержит подмножества, также являющегося суперключем данного отношения. Т.о. потенциальный ключ обладает свойствами уникальности и неприводимости.
Первичный ключ – это потенциальный ключ, который выбран для уникальной идентификации кортежей внутри отношения
Внешний ключ – это атрибут или множество атрибутов одного отношения, которые принимают значения потенциального ключа другого отношения (может быть и того же)
На схемах названия атрибутов первичного ключа выделяют подчеркиванием
Слайд 8Реляционные ключи
1+2+3+4 – суперключ
1+2+3 – суперключ
2 – потенциальный ключ
3 –
потенциальный ключ
2 – первичный ключ (например)
Студенты
Слайд 9Реляционные ключи
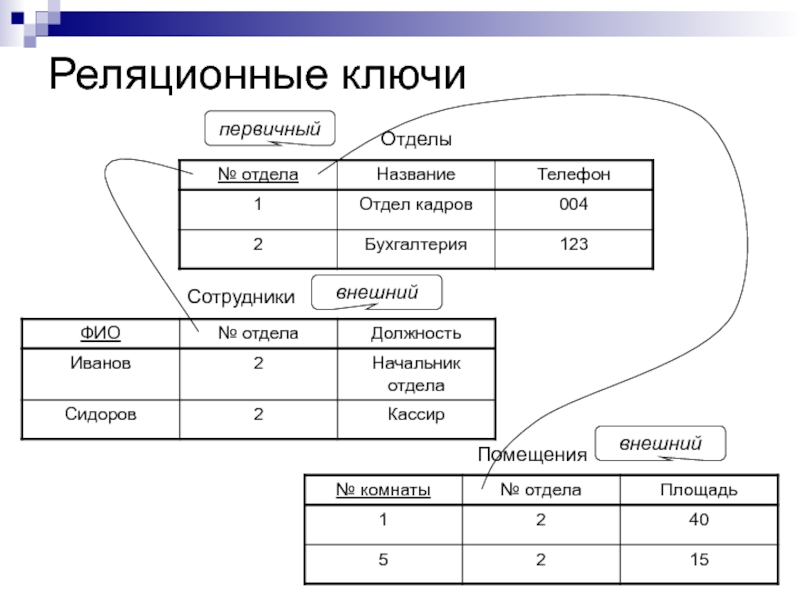
Помещения
Сотрудники
Отделы
внешний
первичный
внешний
Слайд 10Реляционные ключи
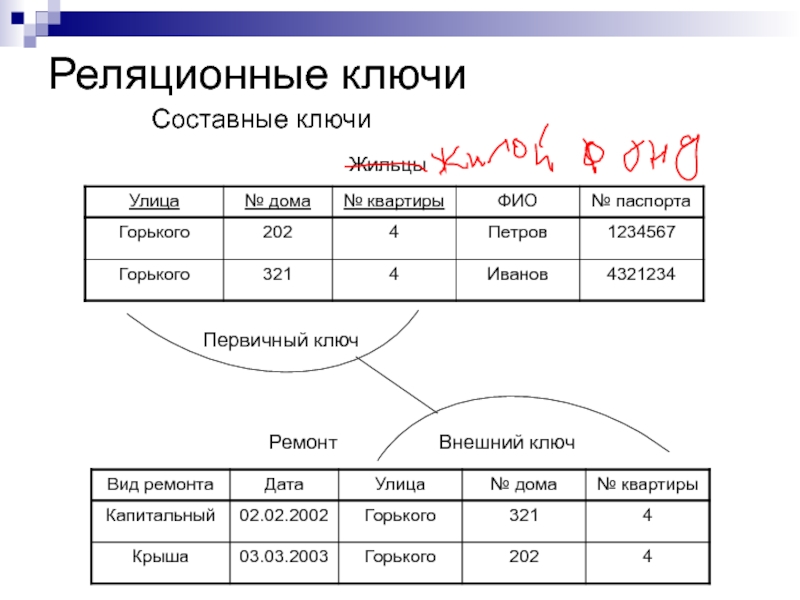
Первичный ключ
Внешний ключ
Составные ключи
Жильцы
Ремонт
Слайд 11Реляционная алгебра
Алгебра – множество элементов с заданной на нем совокупностью
операций, замкнутых относительно этого множества
Реляционная алгебра – множество отношений и
совокупность операций над отношениями
Реляционная база данных – совокупность некоторого числа отношений
Концептуальная модель базы данных (концептуальная схема базы данных) – множество всех реляционных схем отношений
Слайд 12Теоретико-множественные операции
Объединение отношений: R1 ∪ R2 = {r | r∈R1
∨ r∈R2}
Пересечение отношений: R1 ∩ R2 = {r | r∈R1
∧ r∈R2}
Разность отношений: R1 \ R2 = {r | r∈R1 ∧ r∉R2}
Декартово произведение отношений (моделирует ситуацию всех возможных исходов некоторого события):
R1 × R2 = {(r1,r2) | r1∈R1, r2∈R2}
Операции объединения, пересечения и вычитания определены только для отношений с эквивалентными схемами
R1={1,3,5,6} R2={1,6,9} R1∪R2={1,3,5,6,9} R1∩R2={1,6} R1\R2={3,5}
Слайд 13Теоретико-множественные операции
Примеры
R1 = - студенты, сдававшие экзамен
в первый день
R2 = - студенты, сдававшие
экзамен во второй день
R3 = <ФИО, № зач.кн> - студенты, перешедшие на следующий курс
Студенты, сдававшие экзамен 2 раза, но отчисленные
R=(R1∩R2)\R3
Студенты, сдававшие экзамен 1 раз, и сдавшие его
R=((R1\ R2)∩R3) ∪ ((R2\ R1)∩R3)
R1 (фамилии)
R2 (номера зач.кн.)
R1 × R2
Декартово произведение
Слайд 14Специальные операции реляционной алгебры
Горизонтальная выборка (фильтрация, выборка)
R[α(r)]={r | r∈R
∧ α(r)=истина}
где α(r) – предикат от атрибутов отношения
R1=
стипендия>
R2=R1[ФИО=‘Иванов’]
Одноместная (унарная) операция
Слайд 15Специальные операции реляционной алгебры
Проекция
R=, B⊆{ai} – множество
атрибутов
R[B]={r[B]} – отношение с атрибутами B
Проекция – отношение со схемой
B, содержащее кортежи из исходного отношения, после удаления атрибутов, не входящих в B. Дубликаты кортежей из результата удаляются
Одноместная (унарная) операция
Слайд 16Специальные операции реляционной алгебры
R1=
R2=R1[ФИО]
Аналогия
Слайд 17Специальные операции реляционной алгебры
Условное соединение
Двуместная (бинарная) операция
R =
a2, …> T =
θk ∈
{<, >, <=, >=, =, <>} - операции сравнения
β={R.ai θk T.bj}, k=1, km – предикат сравнения, определенный для атрибутов отношений
Тогда
R[β] T= {(r,t) | r∈R, t∈T и β(r.ai θk t.bj)=истина, k=1,km}
Условное соединение – конкатенация кортежей по заданному условию (поэтому условное соединение)
Операция соединения эквивалентна операции декартова произведения и последующей выборке в соответствии с предикатом соединения
Слайд 18Специальные операции реляционной алгебры
Частные случаи условного соединения:
Соединение по эквивалентности. Это
соединение в котором все θk – операции сравнения на равенство
Естественное
соединение. Это соединение по эквивалентности двух отношений R и T, выполняемое по общим атрибутам X, из результатов которого исключаются по одному экземпляру каждого общего атрибута
Внешние соединения. (Будут рассмотрены позже)
R1
R2
R1[R1.y=R2.y]R2
Соединение
по эквивалентности
Естественное
соединение
Слайд 19Примеры
Концептуальная схема базы данных
E = - результаты сдачи
экзаменов
G= - состав группы
P= - набор дисциплин, по
которым надо сдавать экзамены группам
1. Получить список студентов, сдавших на отлично БД
R = ( E[Оценка=5 и Дисц=‘БД’] )[ФИО]
Слайд 20Примеры
2. Получить список тех, кто должен был сдавать экзамен по
БД, но пока еще не сдавал
а) Соединить G и P,
чтобы получить студентов и дисциплины, которые они должны сдавать
R1 = (G[G.Группа = P.Группа и P.Дисц = ‘БД’]P) [ФИО]
б) Получить студентов, сдавших экзамен по БД
R2 = (E[E.Дисц=‘БД’])[ФИО]
в) Вычесть из всех, кто должен сдавать тех, кто уже сдал
R = R1\R2
Слайд 21Примеры
3. Получить список студентов, имеющих несколько двоек (более одной)
Введем E’
– ссылка на то же самое отношение E (переименование отношения).
R
= (E[E.ФИО=E’.ФИО и E.Оц=E’.Оц и E.Оц=2 и E.Дисц<>E’.Дисц]E’)[E.ФИО]
E
E’
Слайд 22Примеры
4. Получить список круглых отличников
а) Получить список студентов, которые должны
что-либо сдавать с соответствующими дисциплинами
R1=(G[G.Группа=P.Группа]P) [ФИО, Дисц]
б) Получить список студентов
и дисциплин, уже сданных на отлично. Но среди студентов будут еще те, которые не все сдали на отлично или что-то еще не сдали.
R2 = (E[Оценка=5])[ФИО, Дисц]
в) Список студентов, что-либо не сдавших на отлично, или не сдавших какие-то экзамены
R3 = (R1\R2)[ФИО]
г) Из всех студентов, которые должны сдавать экзамены, вычесть не сдавших что-либо на отлично и не сдававших какие-то экзамены
R = R1[ФИО]\R3
(здесь нельзя делать G[ФИО]\R3, т.к. в результат попадут студенты, которые не должны сдавать экзамены вообще)
Слайд 23Примеры
Концептуальная модель производства деталей
P= - номенклатура деталей
D= - все
цеха завода
F= - детали, выпускаемые цехами
5. Определить перечень цехов,
в которых выпускаются все детали (вся номенклатура)
R1 = P[Шифр] получить шифры всех деталей
R2 = R1xD моделируется ситуация, когда во всех цехах выпускаются все детали
R3 = R2\F остаются цеха и детали, не выпускаемые в этих цехах
R4 = R3[Цех] цеха, в которых выпускаются не все детали
R5 = D\R4 цеха, в которых выпускаются все детали











![Реляционная модель данных Специальные операции реляционной алгебрыГоризонтальная выборка (фильтрация, выборка) R[α(r)]={r | r∈R ∧ Специальные операции реляционной алгебрыГоризонтальная выборка (фильтрация, выборка) R[α(r)]={r | r∈R ∧ α(r)=истина} где α(r) – предикат от](/img/thumbs/97318fd5247a0c788e31d16a6f0bfdcd-800x.jpg)
![Реляционная модель данных Специальные операции реляционной алгебрыПроекцияR=, B⊆{ai} – множество атрибутовR[B]={r[B]} – отношение с Специальные операции реляционной алгебрыПроекцияR=, B⊆{ai} – множество атрибутовR[B]={r[B]} – отношение с атрибутами BПроекция – отношение со схемой](/img/thumbs/62e90557c3f1d3e957d414d572fd3253-800x.jpg)
![Реляционная модель данных Специальные операции реляционной алгебрыR1=R2=R1[ФИО]Аналогия Специальные операции реляционной алгебрыR1=R2=R1[ФИО]Аналогия](/img/thumbs/68ed06e0fa3a554f4cbfde85caa79255-800x.jpg)





![Реляционная модель данных Примеры4. Получить список круглых отличникова) Получить список студентов, которые должны что-либо Примеры4. Получить список круглых отличникова) Получить список студентов, которые должны что-либо сдавать с соответствующими дисциплинамиR1=(G[G.Группа=P.Группа]P) [ФИО, Дисц]б)](/img/thumbs/643ee07e23ee7005abef82962d97c7e8-800x.jpg)