Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач B9 - Стереометрические задачи
Содержание
- 1. Решение задач B9 - Стереометрические задачи
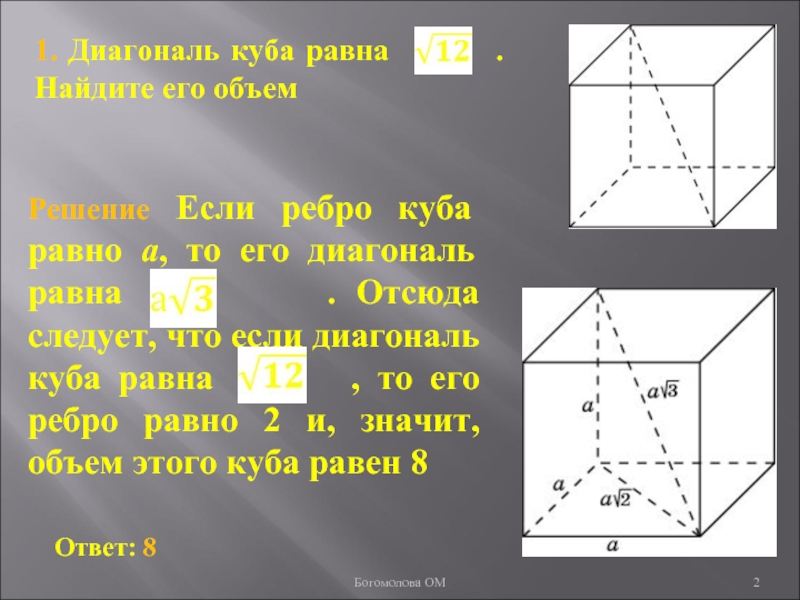
- 2. 1. Диагональ куба равна . Найдите его объемБогомолова ОМ
- 3. 2. Если каждое ребро куба увеличить на
- 4. 3. Гранью параллелепипеда является ромб со стороной
- 5. 4. Через среднюю линию основания треугольной призмы,
- 6. 5. Во сколько раз увеличится объем правильного
- 7. 6. Стороны основания правильной шестиугольной пирамиды равны
- 8. 7. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямыеБогомолова ОМ
- 9. 8. Найдите объем пирамиды, изображенной на рисунке.
- 10. 9. В цилиндрический сосуд, в котором находится
- 11. 10. Радиусы двух шаров равны 6 и
- 12. 11. Прямоугольный параллелепипед описан около цилиндра, радиус
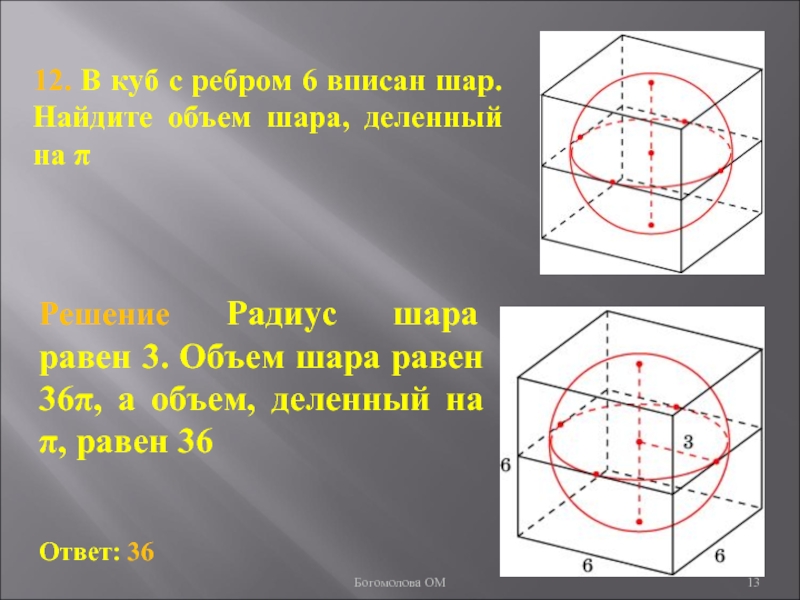
- 13. 12. В куб с ребром 6 вписан шар. Найдите объем шара, деленный на πБогомолова ОМ
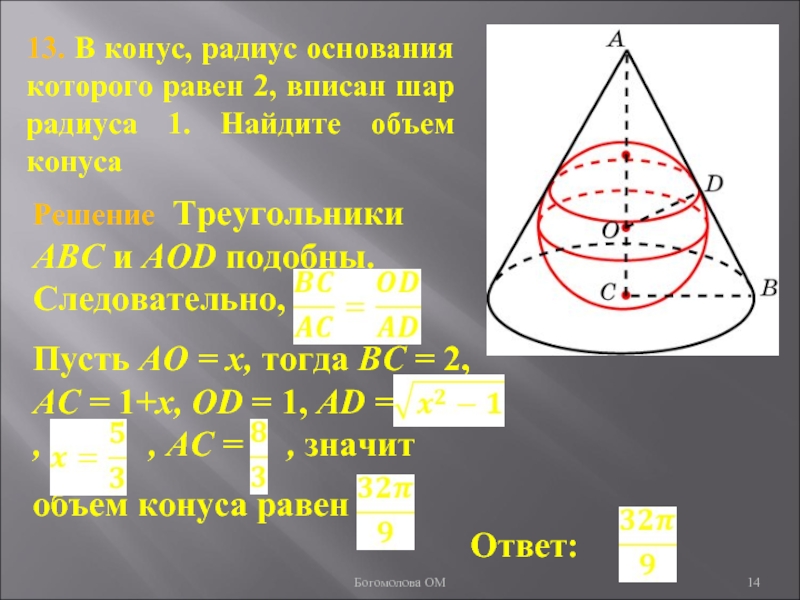
- 14. 13. В конус, радиус основания которого равен 2, вписан шар радиуса 1. Найдите объем конусаБогомолова ОМ
- 15. 14. В сферу радиуса 5 вписан конус, высота которого равна 8. Найдите объем конусаБогомолова ОМ
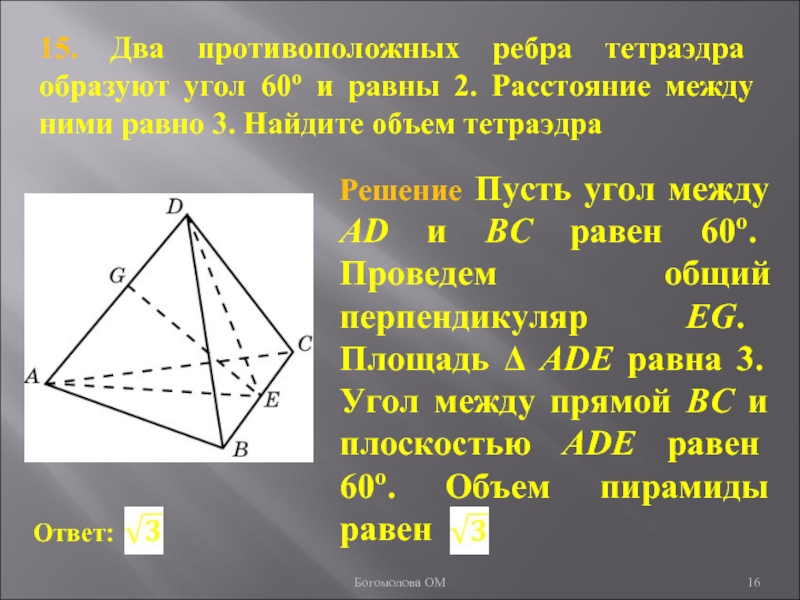
- 16. 15. Два противоположных ребра тетраэдра образуют угол
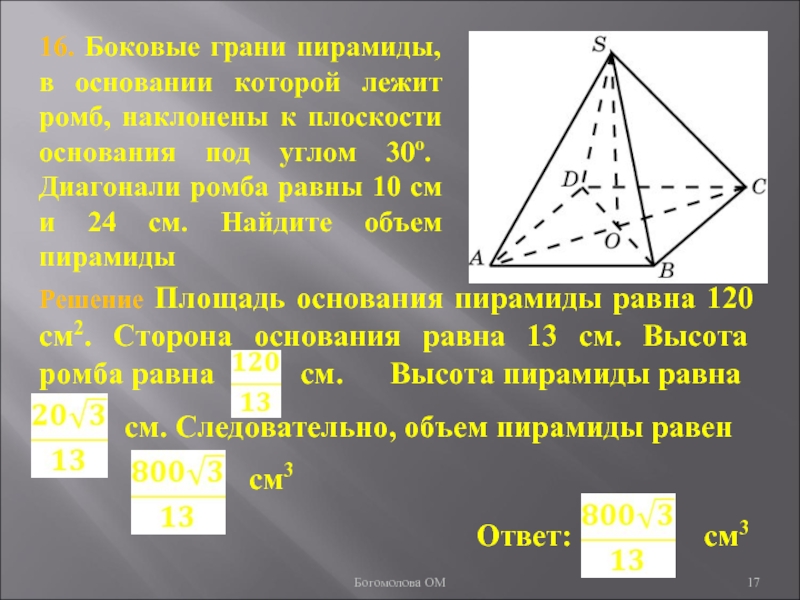
- 17. 16. Боковые грани пирамиды, в основании которой
- 18. 17. Основанием пирамиды служит прямоугольник, одна боковая
- 19. 18. Найдите объем правильной треугольной призмы, описанной около единичной сферыБогомолова ОМ
- 20. 19. Боковые ребра наклонной треугольной призмы равны
- 21. Скачать презентанцию
1. Диагональ куба равна . Найдите его объемБогомолова ОМ
Слайды и текст этой презентации
Слайд 32. Если каждое ребро куба увеличить на 1, то его
площадь поверхности увеличится на 30. Найдите ребро куба
Богомолова ОМ
Слайд 43. Гранью параллелепипеда является ромб со стороной 1 и острым
углом 60о. Одно из ребер параллелепипеда составляет с этой гранью
угол в 60о и равно 2. Найдите объем параллелепипедаБогомолова ОМ
Слайд 54. Через среднюю линию основания треугольной призмы, объем которой равен
32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной
призмыБогомолова ОМ
Слайд 65. Во сколько раз увеличится объем правильного тетраэдра, если все
его ребра увеличить в два раза?
Богомолова ОМ
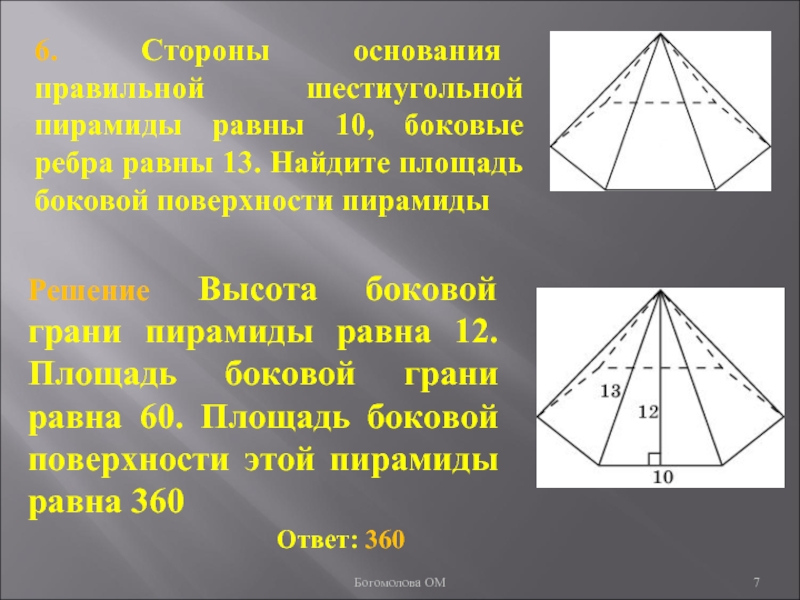
Слайд 76. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра
равны 13. Найдите площадь боковой поверхности пирамиды
Богомолова ОМ
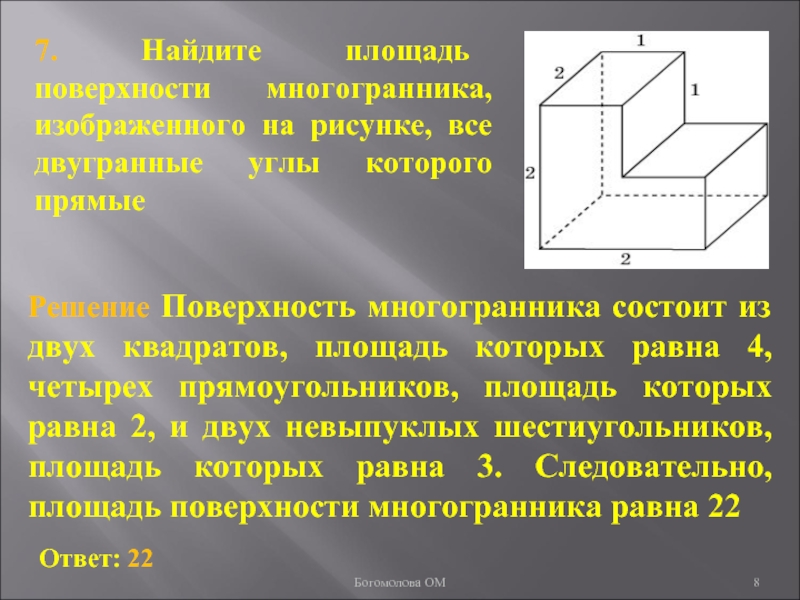
Слайд 87. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные
углы которого прямые
Богомолова ОМ
Слайд 98. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является
многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер
перпендикулярно плоскости основания и равно 3Богомолова ОМ
Слайд 109. В цилиндрический сосуд, в котором находится 6 дм3 воды,
опущена деталь. При этом уровень жидкости в сосуде поднялся в
1,5 раза. Чему равен объем детали?Богомолова ОМ
Слайд 1110. Радиусы двух шаров равны 6 и 8. Найдите радиус
шара, площадь поверхности которого равна сумме площадей их поверхностей
Богомолова ОМ
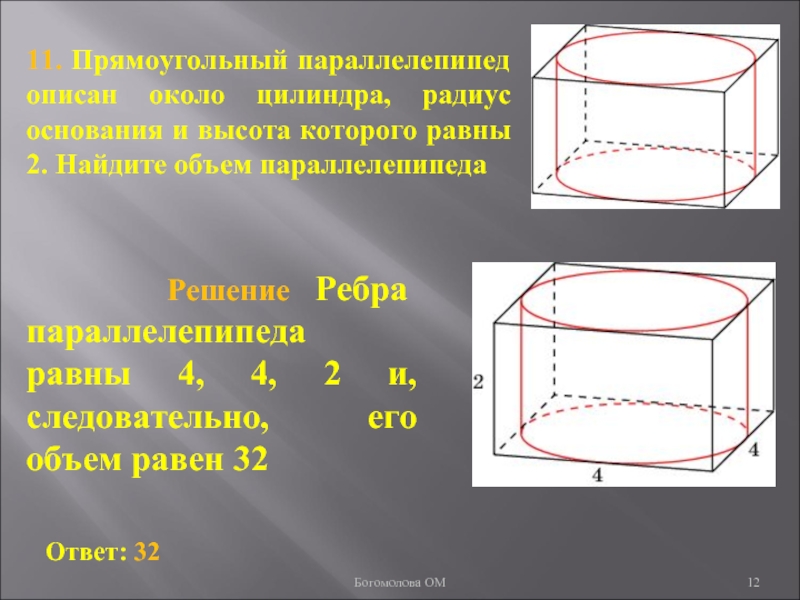
Слайд 1211. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота
которого равны 2. Найдите объем параллелепипеда
Богомолова ОМ
Слайд 1413. В конус, радиус основания которого равен 2, вписан шар
радиуса 1. Найдите объем конуса
Богомолова ОМ
Слайд 1514. В сферу радиуса 5 вписан конус, высота которого равна
8. Найдите объем конуса
Богомолова ОМ
Слайд 1615. Два противоположных ребра тетраэдра образуют угол 60о и равны
2. Расстояние между ними равно 3. Найдите объем тетраэдра
Богомолова ОМ
Слайд 1716. Боковые грани пирамиды, в основании которой лежит ромб, наклонены
к плоскости основания под углом 30о. Диагонали ромба равны 10
см и 24 см. Найдите объем пирамидыБогомолова ОМ
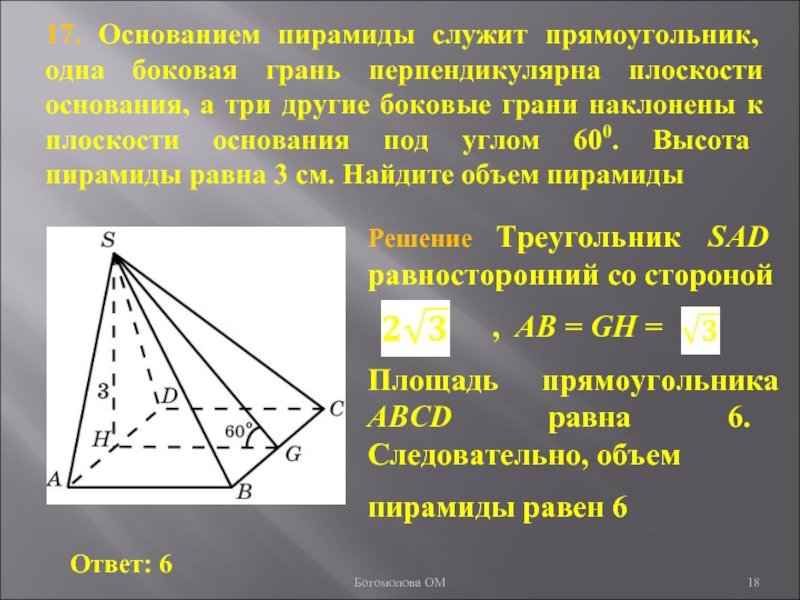
Слайд 1817. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости
основания, а три другие боковые грани наклонены к плоскости основания
под углом 600. Высота пирамиды равна 3 см. Найдите объем пирамидыБогомолова ОМ
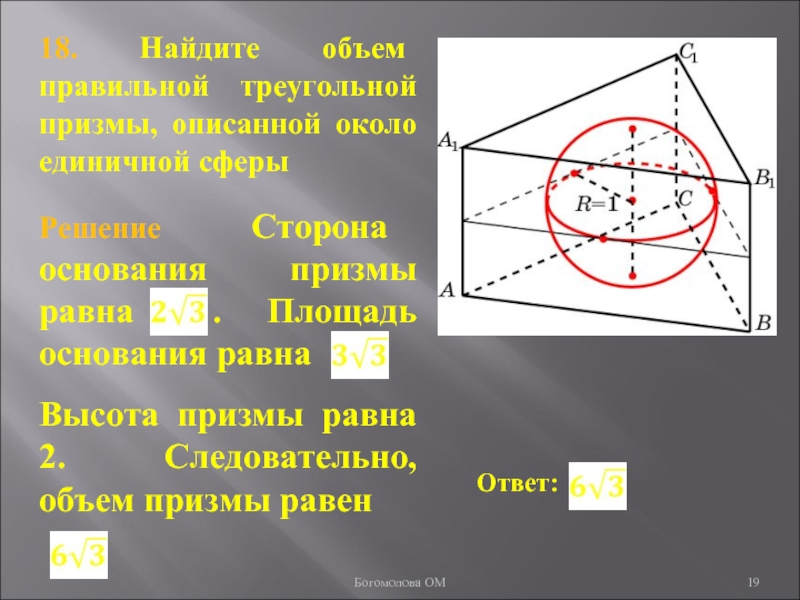
Слайд 1918. Найдите объем правильной треугольной призмы, описанной около единичной сферы
Богомолова
ОМ
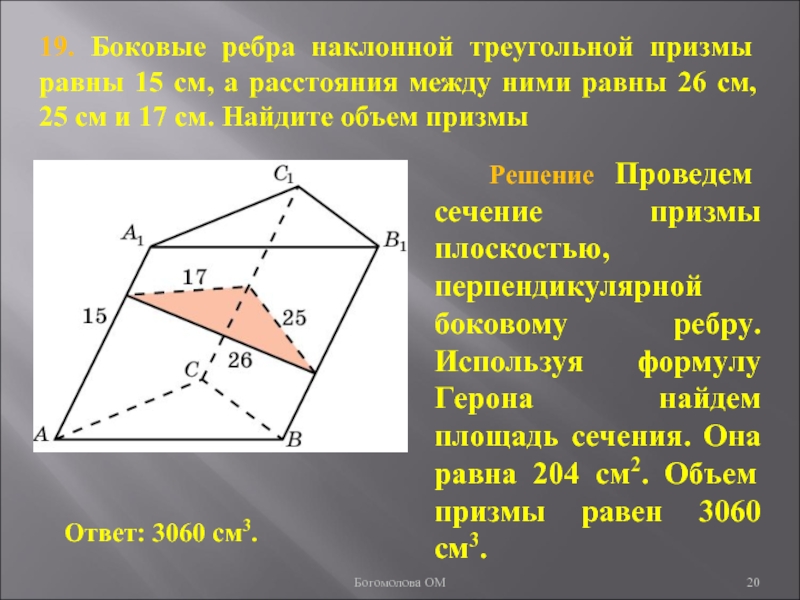
Слайд 2019. Боковые ребра наклонной треугольной призмы равны 15 см, а
расстояния между ними равны 26 см, 25 см и 17
см. Найдите объем призмыБогомолова ОМ
Теги