Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач на применение производной
Содержание
- 1. Решение задач на применение производной
- 2. Если функция дифференцируема на всей области определения , то графиком функции являетсягладкая кривая
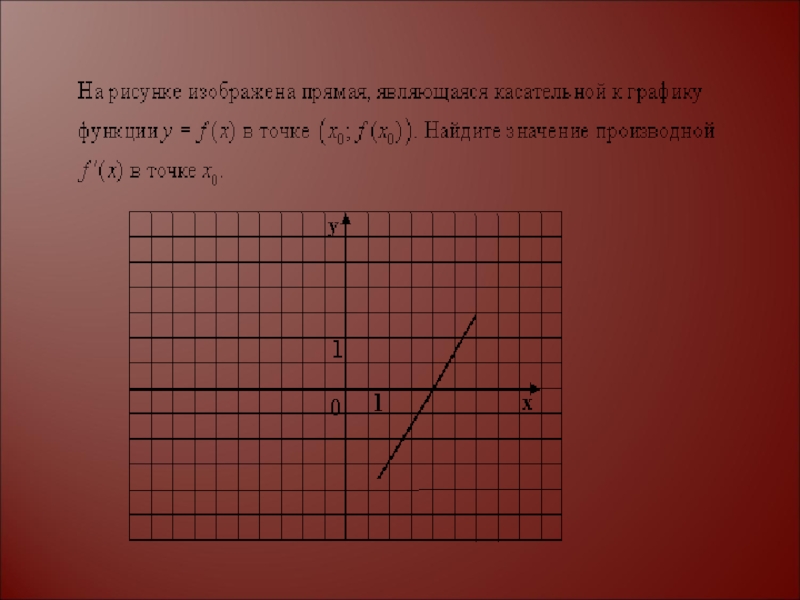
- 3. КАСАТЕЛЬНАЯ(х๐;f(x๐)) – координаты точки касанияУравнение касательной y=f´(x๐)·(x-x๐)+f(x๐)y=kx+b
- 4. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙk=f´(x๐)=tgαk- угловой коэффициент касательнойα-угол наклона
- 5. ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙY=S(t)- зависимость пути от времениS´(t)=V(t)- зависимость скорости от времениS´´(t)=V´(t)=a(t)-зависимость ускорения от времени
- 6. НАХОЖДЕНИЕ ПРОМЕЖУТКОВ МОНОТОННОСТИf´(x)=0- условие нахождения критических точекЕсли
- 7. НАХОЖДЕНИЕ ТОЧЕК ЭКСТРЕМУМА И ЭКСТРЕМУМОВ ФУНКЦИИ1.Область определения
- 8. НАХОЖДЕНИЕ НАИБОЛЬШЕГО ИЛИ НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ НА
- 9. Слайд 9
- 10. №3На рисунке изображен график производной функции f(x), определенной
- 11. №4 НА РИСУНКЕ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ F(X), ОПРЕДЕЛЕННОЙ
- 12. №5 НА РИСУНКЕ ИЗОБРАЖЕН ГРАФИК ПРОИЗВОДНОЙ ФУНКЦИИ F(X)
- 13. №6 НА РИСУНКЕ ИЗОБРАЖЕН ГРАФИК ПРОИЗВОДНОЙ ФУНКЦИИ F(X),
- 14. №7 НА РИСУНКЕ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ , ОПРЕДЕЛЕННОЙ
- 15. Скачать презентанцию
Если функция дифференцируема на всей области определения , то графиком функции являетсягладкая кривая
Слайды и текст этой презентации
Слайд 3КАСАТЕЛЬНАЯ
(х๐;f(x๐)) – координаты точки касания
Уравнение касательной
y=f´(x๐)·(x-x๐)+f(x๐)
y=kx+b
Слайд 4ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
k=f´(x๐)=tgα
k- угловой коэффициент касательной
α-угол наклона касательной к положительному
направлению оси Ох
k>0, α-острый
k
α-тупойk=0, касательная параллельна оси Ох (α=0)
Слайд 5ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Y=S(t)- зависимость пути от времени
S´(t)=V(t)- зависимость скорости от
времени
S´´(t)=V´(t)=a(t)-зависимость ускорения от времени
Слайд 6НАХОЖДЕНИЕ ПРОМЕЖУТКОВ МОНОТОННОСТИ
f´(x)=0- условие нахождения критических точек
Если f´(x)>0 на промежутке
(a;b), то функция возрастает на промежутке (a;b)
Если f´(x)
промежутке (a;b), то функция убывает на промежутке (a;b)Слайд 7НАХОЖДЕНИЕ ТОЧЕК ЭКСТРЕМУМА И ЭКСТРЕМУМОВ ФУНКЦИИ
1.Область определения функции
2.Найти производную
3.Найти критические
точки
f ’ (x)
+ - +4. f(x) x₁ x₂ x
5.Ответ
Слайд 8НАХОЖДЕНИЕ НАИБОЛЬШЕГО ИЛИ НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ НА ОТРЕЗКЕ
1.найти область определения
функции
2.найти производную функции
3.найти критические точки
4.Найти значения функции на концах отрезка
и в критических точках, принадлежащих данному отрезку5.Выбрать наибольшее или наименьшее значения функции
Слайд 10
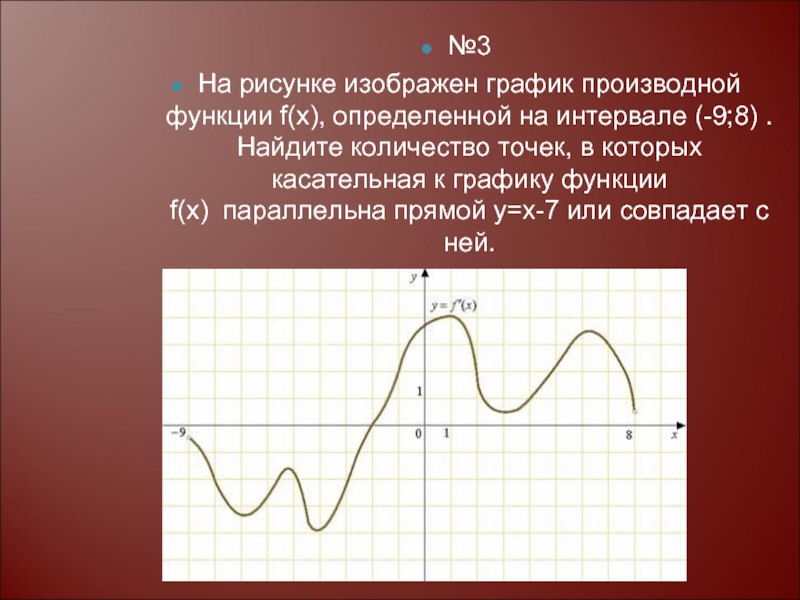
№3
На рисунке изображен график производной функции f(x), определенной на интервале (-9;8)
. Найдите количество точек, в которых касательная к графику функции
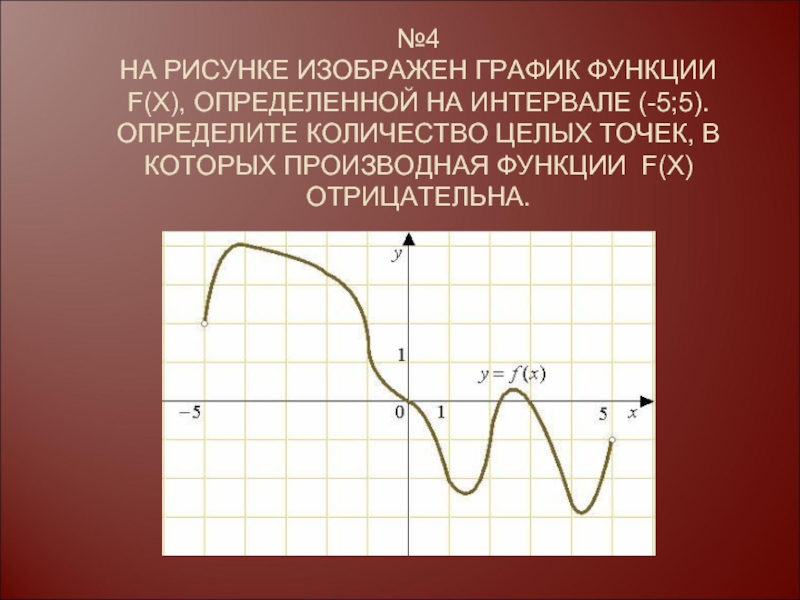
f(x) параллельна прямой y=x-7 или совпадает с ней.Слайд 11№4 НА РИСУНКЕ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ F(X), ОПРЕДЕЛЕННОЙ НА ИНТЕРВАЛЕ (-5;5). ОПРЕДЕЛИТЕ
КОЛИЧЕСТВО ЦЕЛЫХ ТОЧЕК, В КОТОРЫХ ПРОИЗВОДНАЯ ФУНКЦИИ F(X) ОТРИЦАТЕЛЬНА.
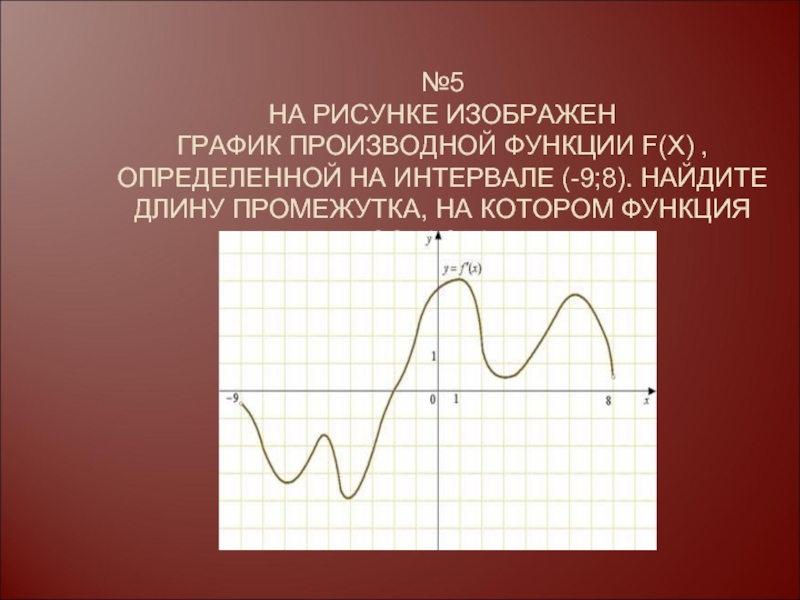
Слайд 12№5 НА РИСУНКЕ ИЗОБРАЖЕН ГРАФИК ПРОИЗВОДНОЙ ФУНКЦИИ F(X) , ОПРЕДЕЛЕННОЙ НА ИНТЕРВАЛЕ
(-9;8). НАЙДИТЕ ДЛИНУ ПРОМЕЖУТКА, НА КОТОРОМ ФУНКЦИЯ ВОЗРАСТАЕТ.
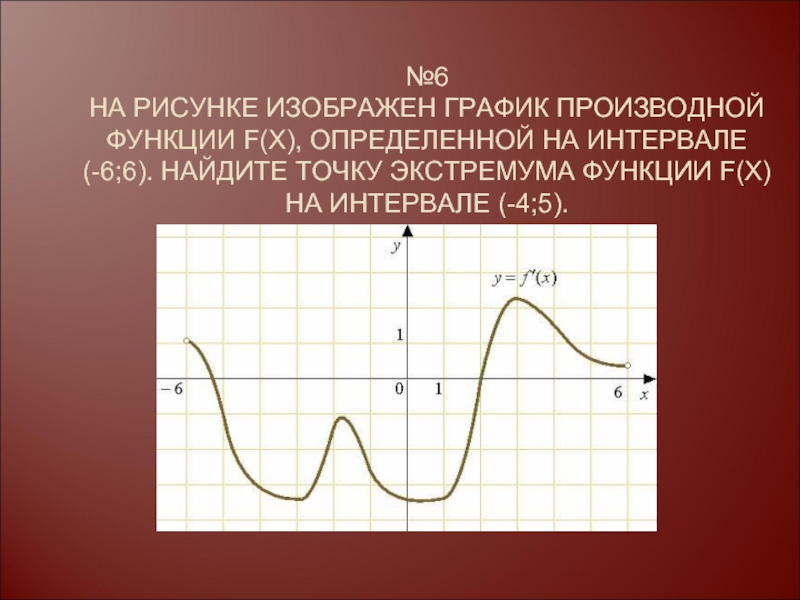
Слайд 13№6 НА РИСУНКЕ ИЗОБРАЖЕН ГРАФИК ПРОИЗВОДНОЙ ФУНКЦИИ F(X), ОПРЕДЕЛЕННОЙ НА ИНТЕРВАЛЕ (-6;6).
НАЙДИТЕ ТОЧКУ ЭКСТРЕМУМА ФУНКЦИИ F(X) НА ИНТЕРВАЛЕ (-4;5).
Слайд 14№7 НА РИСУНКЕ ИЗОБРАЖЕН ГРАФИК ФУНКЦИИ , ОПРЕДЕЛЕННОЙ НА ИНТЕРВАЛЕ . НАЙДИТЕ
КОЛИЧЕСТВО ТОЧЕК, В КОТОРЫХ КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ ПАРАЛЛЕЛЬНА ПРЯМОЙ
.
Теги