Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Розділ 3. Абстрактні типи даних
Содержание
- 1. Розділ 3. Абстрактні типи даних
- 2. 3.9. АТД “Дерево”Література для самостійного читання: с. 77-89 [1], с. 326-330 [4]
- 3. Розглянуті раніше списки, стеки та черги належать
- 4. Представлення дерев за допомогою масивів Нехай Т -
- 5. Слайд 5
- 6. Використання покажчиків або курсорів на батьків не
- 7. Представлення дерев з використанням списків синів Важливий
- 8. З прикладом реалізації можна ознайомитись в (с.87-88 [1]).
- 9. Серед недоліків такої структури даних можна назвати
- 10. 3.10. Бінарні дереваЛітература для самостійного читання: с. 91-99 [1], с. 328-336 [4]
- 11. Представлення бінарних дерев за допомогою масивів Якщо іменами
- 12. Представлення бінарних дерев за допомогою нелінійних динамічних
- 13. Приклад бінарного дерева як динамічної структури даних
- 14. Алгоритми роботи з бінарними деревами Створення бінарного дерева Найпростіший
- 15. Приклад. Створення бінарного дерева із заданою користувачем
- 16. Функція створення дерева tree отримує один цілочисловий
- 17. Слайд 17
- 18. Дерево відображатиме рекурсивна процедура printtree. Піддерево рівня
- 19. Слайд 19
- 20. Обхід дерева Алгоритм доступу до всіх вузлів дерева
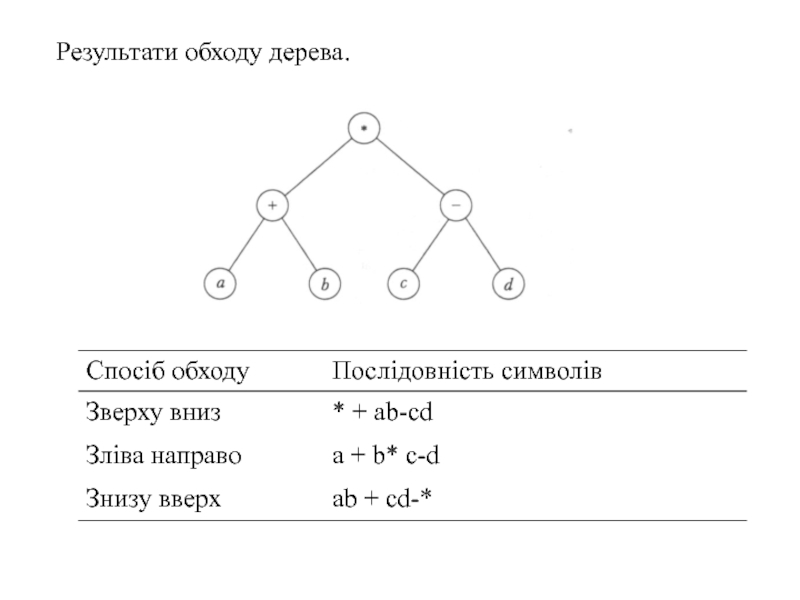
- 21. Результати обходу дерева.
- 22. Будь-який спосіб обходу дерева можна реалізувати рекурсивною
- 23. Слайд 23
- 24. Слайд 24
- 25. Дерева бінарного пошуку Бінарні дерева часто використовуються для
- 26. Вузол із заданим значенням ключа буде знайдений
- 27. Приклад. Функція знаходження ключового значення в бінарному
- 28. Слайд 28
- 29. Слайд 29
- 30. Включення вузлів у дерево Дерева змінної структури, тобто
- 31. Приклад. Включення вузла в бінарне дерево пошуку.
- 32. У програмі, що реалізує пошук із включенням,
- 33. Слайд 33
- 34. Слайд 34
- 35. Видалення вузлів бінарного дерева Можливі три випадки видалення
- 36. Якщо видаляється вузол х, який має одного
- 37. Якщо видаляється вузол х, який має двох
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Домашнє завдання Прочитати с.23-83 [1] , с.310-341 [4] Підготуватися до виконання практичної роботи №3.
- 44. Скачать презентанцию
3.9. АТД “Дерево”Література для самостійного читання: с. 77-89 [1], с. 326-330 [4]
Слайды и текст этой презентации
Слайд 3 Розглянуті раніше списки, стеки та черги належать до лінійних динамічних
структур даних. Визначальною характеристикою лінійних структур є те, що зв'язок
між їхніми компонентами описується в термінах «попередній-наступний», тобто для кожного компонента лінійної структури визначено не більше одного попереднього та не більше одного наступного компонента.Деревоподібна структура даних, або дерево, є нелінійною структурою, що зображує ієрархічні зв'язки типу «предок-нащадок»: компонент-предок може мати багато нащадків, хоча для кожного компонента-нащадка визначено не більше одного предка.
Щоб згадати термінологію можна почитати (с.77-83 [1], с.326-327 [4] ).
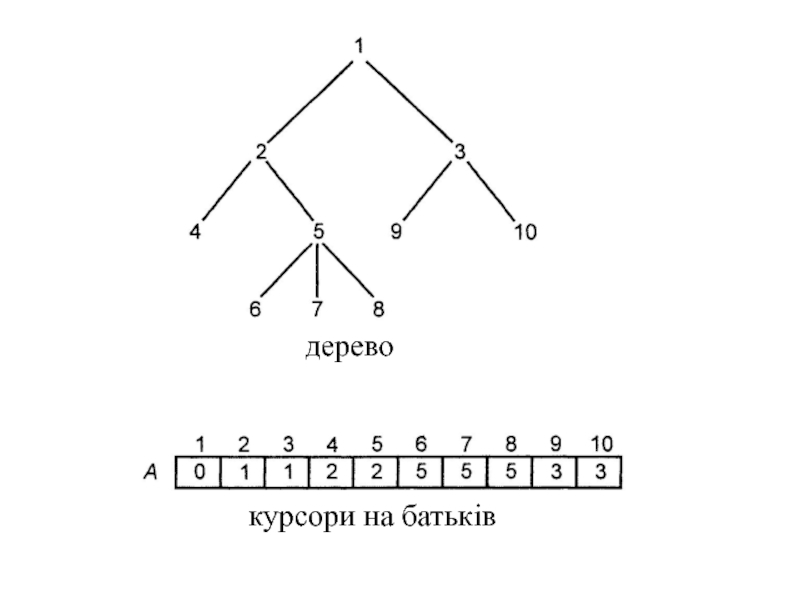
Слайд 4 Представлення дерев за допомогою масивів
Нехай Т - дерево з вузлами
1, 2 ..., n. Найпростішим представленням дерева Т, що підтримує
оператор визначення батька вузла, буде лінійний масив А, де кожен елемент А[i] є покажчиком або курсором на батька вузла i. Корінь дерева Т відрізняється від інших вузлів тим, що має нульовий покажчик або покажчик на самого себе як на батька.Дане уявлення використовує властивість дерев, що кожен вузол, відмінний від кореня, має тільки одного батька. Використовуючи це уявлення, батька будь-якого вузла можна знайти за фіксований час. Проходження по будь-якому шляху, тобто перехід по вузлах від батька до батька, можна виконати за час, пропорційний кількості вузлів шляху.
Слайд 6 Використання покажчиків або курсорів на батьків не допомагає в реалізації
операторів, що вимагають інформацію про синів. Використовуючи описане представлення, вкрай
важко для даного вузла n знайти його синів або визначити його висоту. Крім того, в цьому випадку неможливо визначити порядок синів вузла (тобто який син знаходиться правішим або лівішим за іншого сина).З прикладом реалізації можна ознайомитись в (с.86 [1]).
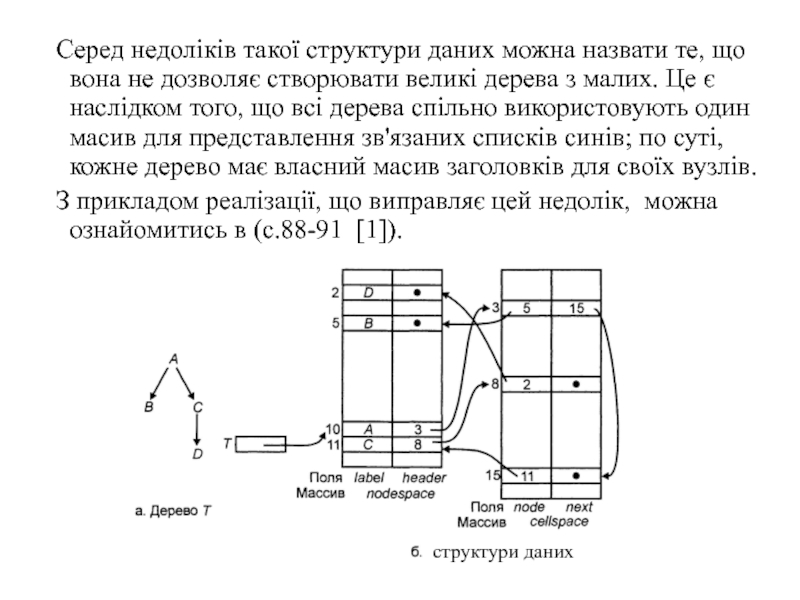
Слайд 7Представлення дерев з використанням списків синів
Важливий і корисний спосіб
представлення дерев полягає у формуванні для кожного вузла списку його
синів. Ці списки можна представити будь-яким методом для представлення списків, але, оскільки число синів у різних вузлів може бути різним, найчастіше для цих цілей застосовуються зв'язані списки.Слайд 9 Серед недоліків такої структури даних можна назвати те, що вона
не дозволяє створювати великі дерева з малих. Це є наслідком
того, що всі дерева спільно використовують один масив для представлення зв'язаних списків синів; по суті, кожне дерево має власний масив заголовків для своїх вузлів.З прикладом реалізації, що виправляє цей недолік, можна ознайомитись в (с.88-91 [1]).
структури даних
Слайд 11 Представлення бінарних дерев за допомогою масивів
Якщо іменами вузлів бінарного дерева
є їх номери 1,2, … n, то підходящою структурою для
представлення цього дерева може бути масив записів з полями “лівий син” та “правий син”.Слайд 12 Представлення бінарних дерев за допомогою нелінійних динамічних структур
Будь-який вузол бінарного
дерева може бути зв'язаним не більше ніж із двома піддеревами,
що називаються лівим і правим піддеревами вузла. Оголошення типу вузла бінарного дерева на мові Pascal може бути таким:Для листків покажчики left та right мають значення nil
Слайд 14 Алгоритми роботи з бінарними деревами
Створення бінарного дерева
Найпростіший спосіб побудови бінарного
дерева полягає у створенні дерева симетричної структури із наперед відомою
кількістю вузлів. Усі вузли-нащадки, що створюються, рівномірно розподіляються зліва та справа від кожного вузла-предка. При цьому досягається мінімально можлива глибина для заданої кількості вузлів дерева. Правило рівномірного розподілу п вузлів можна визначити рекурсивно:перший вузол вважати коренем дерева;
створити ліве піддерево з кількістю вузлів nleft=п div 2;
створити праве піддерево з кількістю вузлів nright=п-nleft–1.
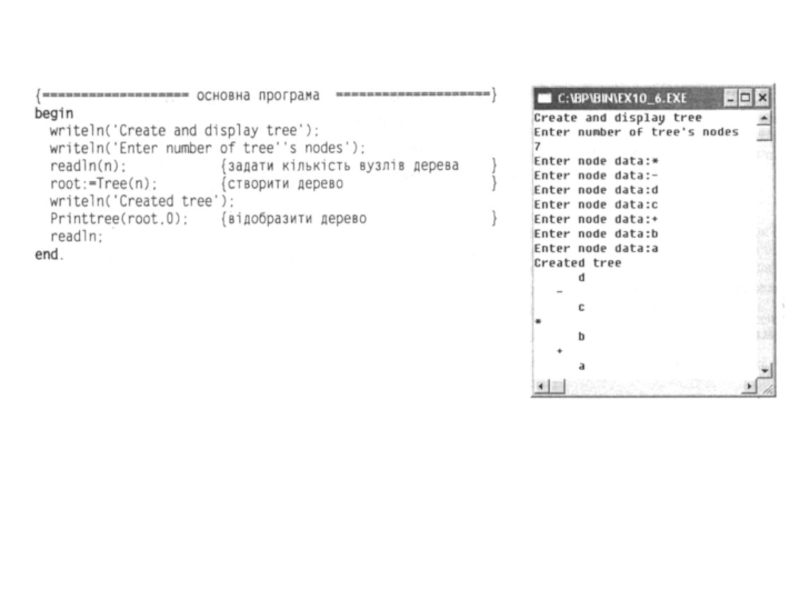
Слайд 15 Приклад. Створення бінарного дерева із заданою користувачем кількістю вузлів.
Оскільки структура дерева визначена рекурсивно, то для його створення та
відображення можна розробити рекурсивні підпрограми.Слайд 16 Функція створення дерева tree отримує один цілочисловий параметр AmountNode, що
визначає кількість вузлів дерева та повертає покажчик на його корінь.
Якщо кількість вузлів дорівнює нулю, дерево порожнє, а отже, виконано умову завершення рекурсії і функція має повернути значення nil. Якщо кількість вузлів дерева відрізняється від нуля, необхідно виділити пам'ять для кореня дерева, за наведеними вище формулами обчислити кількість вузлів у лівому та правому піддеревах і двічі рекурсивно викликати функцію tree для створення піддерев. Для посилання на корінь дерева використано локальний покажчик newnode. Значення покажчиків на корені піддерев, що їх повертатиме функція tree в результаті рекурсивних викликів, слід присвоїти полям left та right змінної newnode^.Слайд 18 Дерево відображатиме рекурсивна процедура printtree. Піддерево рівня L виводитиметься так:
спочатку буде відображене ліве піддерево, потім - корінь піддерева рівня
L, перед яким буде виведено L пробілів, далі - праве піддерево.Слайд 20 Обхід дерева
Алгоритм доступу до всіх вузлів дерева називається обходом дерева.
Трьома основними способами обходу дерева є обхід зверху вниз (в
прямому порядку), зліва направо (в симетричному порядку) та знизу вверх (в зворотньому порядку).У результаті обходу синтаксичного дерева зверху вниз утворюється префіксна форма виразу, при обході знизу вверх — постфіксна форма, а при обході зліва направо — інфіксна форма.
Слайд 22 Будь-який спосіб обходу дерева можна реалізувати рекурсивною процедурою.
До цих процедур
передається параметр-значення, що є покажчиком на корінь дерева. Тіло всіх
трьох процедур містить однаковий набір операторів. Першою виконується перевірка того, чи не є дерево порожнім. Якщо дерево порожнє, здійснюється рекурсивне повернення, а в іншому разі виводиться значення вузла і рекурсивно викликаються процедури обходу для лівого та правого піддерев. Порядок цих трьох операторів і визначає форму виразу, що буде створений у результаті обходу. А саме, якщо виведення значення вузла виконуватиметься першим, то буде отримано префіксну форму виразу, якщо другим — інфіксну, а якщо третім — постфіксну форму.Слайд 25 Дерева бінарного пошуку
Бінарні дерева часто використовуються для зображення множин, елементи
яких потрібно знаходити за заданим значенням ключа. Такі дерева називаються
деревами бінарного пошуку. Особливість подібного дерева полягає в тому, що для будь-якого його вузла х значення всіх вузлів лівого піддерева х не більші за значення х, а значення всіх вузлів правого піддерева х не менші за значення х. Така властивість називається впорядкованістю ключів у дереві.Слайд 26 Вузол із заданим значенням ключа буде знайдений доволі швидко, якщо
спускатися від кореня дерева бінарного пошуку за таким правилом: ліве
піддерево обирається тоді, коли значення розглядуваного вузла більше за шукане, а праве піддерево — тоді, коли вказане значення менше за шукане. Якщо значення вузла дорівнює шуканому, пошук слід завершити. Якщо пошук привів до порожньої гілки дерева, то ключового значення в дереві немає.Для знаходження за таким алгоритмом значення ключа серед n-елементної множини буде переглянуто O(log п) елементів.
Слайд 27 Приклад. Функція знаходження ключового значення в бінарному дереві пошуку.
До
функції передається ключове значення і покажчик на корінь дерева, а
повертає функція покажчик на вузол, значення якого дорівнює шуканому. Як ознаку успішності пошуку використано логічну змінну found. Пошук починається з кореня дерева і триває доти, доки шукане значення не буде знайдене або доки всі вузли дерева не будуть перевірені.Слайд 30 Включення вузлів у дерево
Дерева змінної структури, тобто такі, кількість елементів
яких під час роботи певної програми може збільшуватися або зменшуватися,
можна використовувати, зокрема, при створенні частотного словника. Задача створення частотного словника формулюється так: потрібно визначити, скільки разів зустрічається кожне слово в заданій послідовності слів.Послідовність слів можна зобразити у вигляді дерева бінарного пошуку. В інформаційних полях вузла такого дерева зберігатиметься слово і кількість його повторень. У разі виявлення в тексті чергового слова дерево переглядають, починаючи з кореневого вузла. Якщо слово в дереві знайдене, то лічильник його повторень збільшується. Але якщо слово в дереві не знайдене, воно включається в дерево із значенням лічильника, що дорівнює 1.
Дану задачу називають іще пошуком із включенням.
Слайд 31 Приклад. Включення вузла в бінарне дерево пошуку.
Включення вузла в
дерево має здійснюватися так, щоб не порушувалася властивість упорядкованості ключів.
Це правило буде дотримане, якщо застосувати розглянутий раніше алгоритм знаходження ключового значення у бінарному дереві пошуку, а включення нового елемента здійснювати тоді, коли пошук завершився безуспішно.Слайд 32 У програмі, що реалізує пошук із включенням, компоненти бінарного дерева
містять два інформаційні поля: поле рядкового типу для збереження слова
та цілочислове поле для збереження кількості повторень слова.Слайд 35 Видалення вузлів бінарного дерева
Можливі три випадки видалення вузла бінарного дерева
пошуку :
вузол, що видаляється, є листком дерева;
вузол, що
видаляється, має одного нащадка; вузол, що видаляється, має двох нащадків.
Задача розв'язується найпростішим способом тоді, коли вузол, що видаляється, є листком дерева. У такому разі слід звільнити ділянку динамічної пам'яті, яку цей вузол займав, та присвоїти значення nil покажчикові на даний вузол.
Слайд 36 Якщо видаляється вузол х, який має одного нащадка, то покажчику
на цей вузол слід присвоїти адресу його нащадка і звільнити
пам'ять, яку вузол х займав.Слайд 37 Якщо видаляється вузол х, який має двох нащадків, на місце
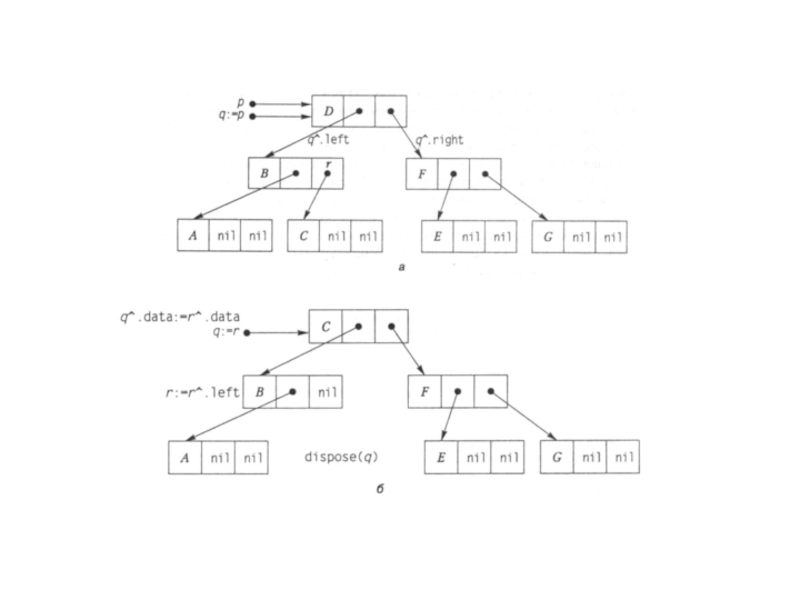
х слід переставити інший вузол дерева так, щоб не порушувалася
властивість впорядкованості ключів. Вузол, що переставляється, називається термінальним.Один із способів визначення термінального вузла полягає у виконанні спуску по правій гілці лівого піддерева х доти, доки не буде знайдено вузла без правого нащадка. Цей вузол і є термінальним, його значення може бути записане до вузла х без порушення впорядкованості ключів. Сам термінальний вузол має бути видалений після копіювання його значення до вузла х.

![Розділ 3. Абстрактні типи даних 3.9. АТД “Дерево”Література для самостійного читання: с. 77-89 [1], с. 326-330 [4] 3.9. АТД “Дерево”Література для самостійного читання: с. 77-89 [1], с. 326-330 [4]](/img/thumbs/b94c2a647cf1be4c9be39a6cf7cff5a4-800x.jpg)




![Розділ 3. Абстрактні типи даних З прикладом реалізації можна ознайомитись в (с.87-88 [1]). З прикладом реалізації можна ознайомитись в (с.87-88 [1]).](/img/thumbs/f7b48531e2ceca4500d6705b6982e6ad-800x.jpg)
![Розділ 3. Абстрактні типи даних 3.10. Бінарні дереваЛітература для самостійного читання: с. 91-99 [1], с. 328-336 [4] 3.10. Бінарні дереваЛітература для самостійного читання: с. 91-99 [1], с. 328-336 [4]](/img/thumbs/30d5c13cd6cd246a8b2e7455f99c9ba3-800x.jpg)





























![Розділ 3. Абстрактні типи даних Домашнє завдання Прочитати с.23-83 [1] , с.310-341 [4] Підготуватися до виконання практичної роботи №3. Домашнє завдання Прочитати с.23-83 [1] , с.310-341 [4] Підготуватися до виконання практичної роботи №3.](/img/thumbs/372feaae49a51cababbb6464e658fafb-800x.jpg)


















