Самоорганизующиеся карты Кохонена

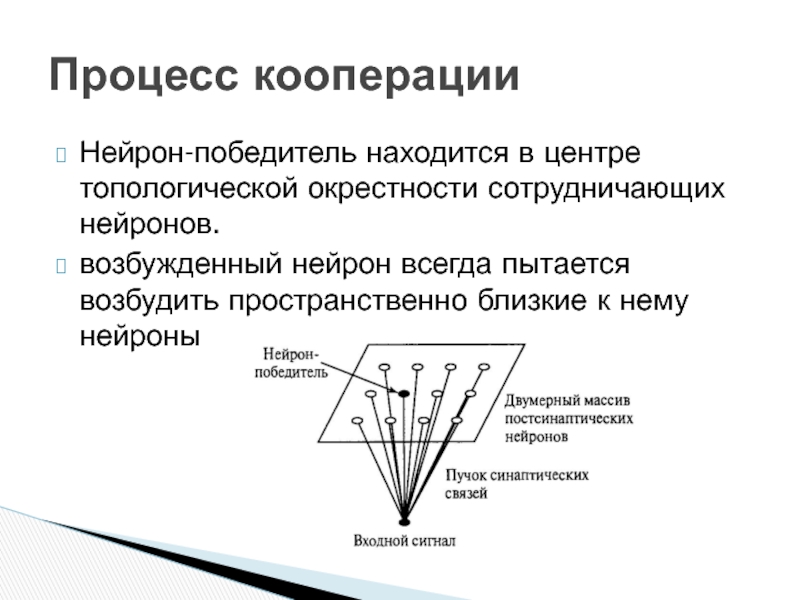
право активации, в результате активным оказывается один нейрон, называемый победителем

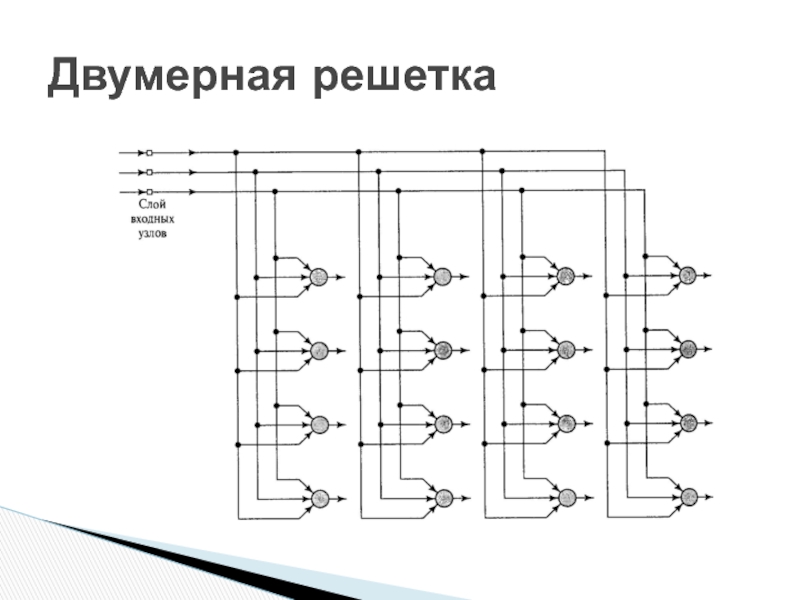
(WTA).
Нейроны помещаются в узлах решетки (одно- или двумерной).
Нейроны в ходе конкурентного процесса избирательно настраиваются на различные входные образы (возбудители) или классы входных образов. Положения таким образом настроенных нейронов (т.е. нейронов-победителей) упорядочиваются по отношению друг к другу так, что на решетке создается система координат

Общие положения

пространственное местоположение (т.е. координаты) нейронов решетки является индикатором встроенных статистических

признаков, содержащихся во входных примерах.

Эта сеть имеет структуру прямого распространения с одним вычислительным слоем,

состоящим из нейронов, упорядоченных в столбцы и строки.
Каждый из входных слоев, представленных в сети, обычно состоит из локализованной области активности, размещаемой в относительно спокойной области. Расположение и природа такой области обычно варьируется в зависимости от конкретной реализации входного примера. Таким образом, для правильного развития процесса самоорганизации требуется, чтобы все нейроны сети были обеспечены достаточным количеством различных реализаций входных образов.

весов сети. Обычно это происходит с помощью назначения синаптическим весам

малых значений, сформированных генератором случайных чисел. При таком формировании карта признаков изначально не имеет какого-либо порядка признаков.После корректной инициализации сети для формирования карты самоорганизации запускаются три следующих основных процесса.

Алгоритм

значения дискриминантной функции. Эта функция является основой конкуренции среди нейронов.

Кооперация (cooperation). Победивший нейрон определяет пространственное положение топологической окрестности нейронов, обеспечивая тем самым базис для кооперации между этими нейронами.
Синаптическая адаптация (synaptic adaptation). Последний механизм позволяет возбужденным нейронам увеличивать собственные значения дискриминантных функций по отношению к входным образам посредством соответствующих коpректировок синаптических весов. Корректировки производятся таким образом, чтобы отклик нейронапобедителя на последующее применение аналогичных примеров усиливался.

входной вектор

- вектор синаптических весов
l – общее количество нейронов сети
Для того чтобы подобрать наилучший вектор wj, соответствующий входному вектору х, нужно сравнить скалярные произведения wjTх для j == 1,2,...,1 и выбрать наибольшее значение.

Процесс конкуренции

насыщения (threshold). Эта величина равна порогу (bias), взятому с обратным

знаком. Таким образом, выбирая нейрон с наибольшим скалярным про изведением wjTх, мы в результате определяем местоположение, которое должно стать центром топологической окрестности возбужденного нейрона
Наилучший критерий соответствия, основанный на максимизации скалярного произведения wjTх, математически эквивалентен минимизации Евклидова расстояния между векторами х и wj.

всего соответствует входному сигналу х, то эту величину можно определить

с помощью следующего соотношения
Конкретный нейрон i, удовлетворяющий данному условию, называется победившим (winning) или наиболее подходящим (bestmatching) для данного входного вектора х.

пытается возбудить пространственно близкие к нему нейроны
Процесс кооперации

нейроне i, состоящую из множества возбуждаемых (кооперирующихся) нейронов, типичный представитель

которой имеет индекс j. Пусть dj,i - латеральное расстояние (lateral distance) между победившим (i) и вторично возбужденным (j) нейронами.

параметр определяет уровень, до которого нейроны из топологической окрестности победившего

участвуют в процессе обучения.

дискретный вектор rj определяет позицию возбуждаемого нейрона j, а ri - победившего нейрона i. Оба этих измерения проводятся в дискретном выходном пространстве.

увеличении количества итераций n ширина σ экспоненциально убывает, соответственно сжимается

топологическая окрестность

Эвристика выбора функции окрестности

Wj(n) в момент времени n обновленный вектор Wj(n + 1)

в момент времени n + 1 можно определить в следующем виде

является формулой вычисления синаптических весов карты признаков

Процесс адаптации

= 1000
η0 = 0,1
Эвристика выбора скорости обучения

в карте признаков не перестанут происходить заметные изменения.