Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ,
Содержание
- 1. САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ,
- 2. Пересечение плоскости с многогранникомПостроение сечения многогранника требует
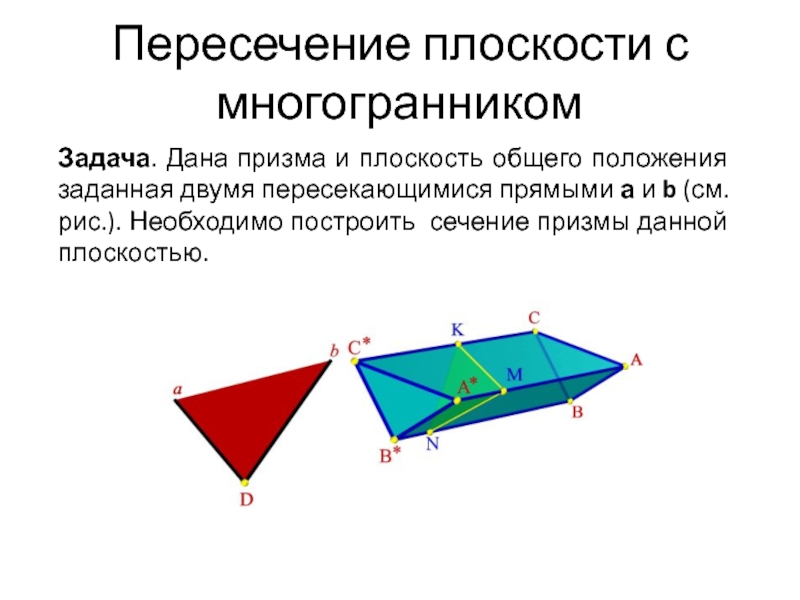
- 3. Пересечение плоскости с многогранникомЗадача. Дана призма и
- 4. Пересечение плоскости с многогранникомДля чего, через горизонтальные
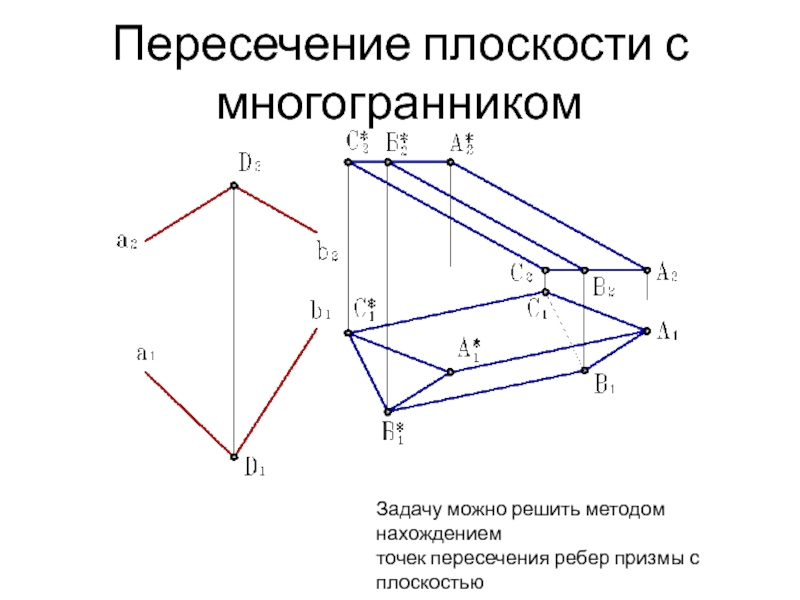
- 5. Пересечение плоскости с многогранникомЗадачу можно решить методом нахождением точек пересечения ребер призмы с плоскостью
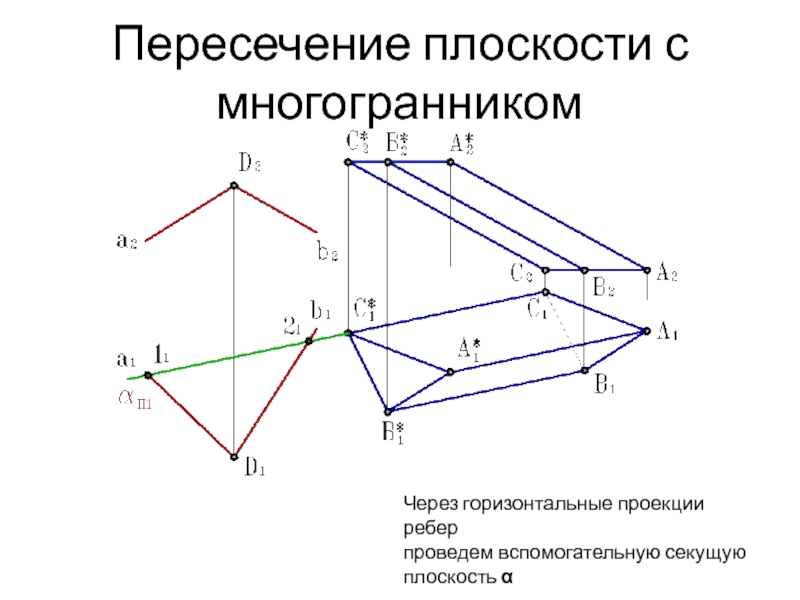
- 6. Пересечение плоскости с многогранникомЧерез горизонтальные проекции ребер проведем вспомогательную секущую плоскость α
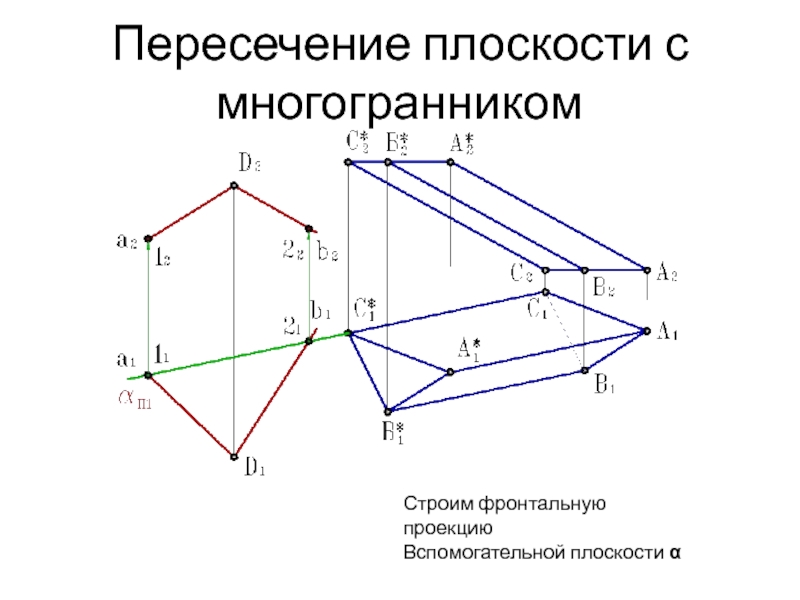
- 7. Пересечение плоскости с многогранникомСтроим фронтальную проекцию Вспомогательной плоскости α
- 8. Пересечение плоскости с многогранникомСтроим фронтальную проекцию Вспомогательной плоскости α
- 9. Пересечение плоскости с многогранникомСтроим точку К2 - точку пересечения вспомогательной плоскости и ребра призмы
- 10. Пересечение плоскости с многогранникомСтроим горизонтальную проекцию точки К - точку К1
- 11. Пересечение плоскости с многогранникомАналогично проводим через горизонтальные проекции ребер вспомогательных секущих плоскостей β и γ.
- 12. Пересечение плоскости с многогранникомАналогично построению точкам К2
- 13. Пересечение плоскости с многогранникомАналогично построению точкам К2
- 14. Пересечение плоскости с многогранникомАналогично построению точкам К2
- 15. Пересечение плоскости с многогранникомАналогично построению точкам К2
- 16. Пересечение прямой линии с многогранникомДля определения точек
- 17. Пересечение прямой с многогранником
- 18. Пересечение прямой с многогранником
- 19. Пересечение прямой с многогранником
- 20. Пересечение прямой с многогранником
- 21. Пересечение прямой с многогранником
- 22. Пересечение прямой с многогранником
- 23. Пересечение прямой с многогранником
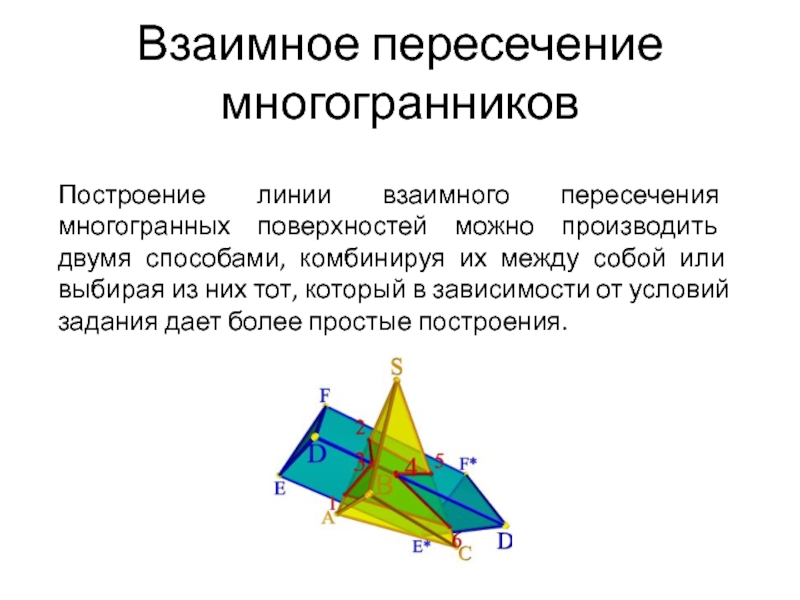
- 24. Взаимное пересечение многогранниковПостроение линии взаимного пересечения многогранных
- 25. Взаимное пересечение многогранников. Способ 1Определяют точки,
- 26. Взаимное пересечение многогранников. Способ 2Определяют отрезки
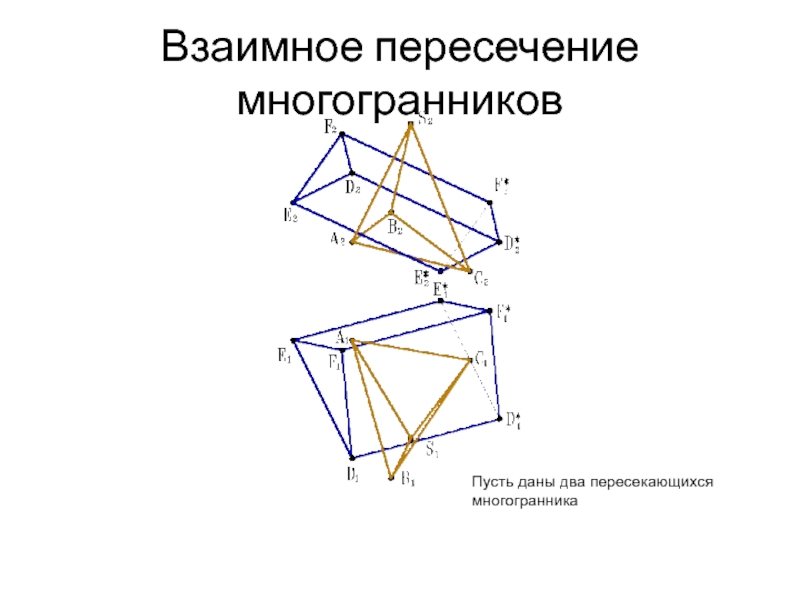
- 27. Взаимное пересечение многогранников Пусть даны два пересекающихся многогранника
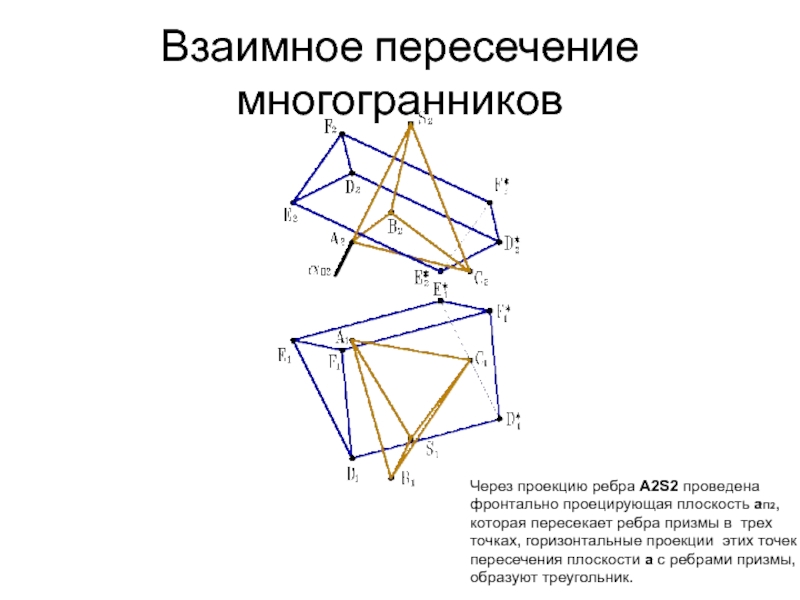
- 28. Взаимное пересечение многогранников Через проекцию ребра A2S2
- 29. Взаимное пересечение многогранников Через проекцию ребра A2S2
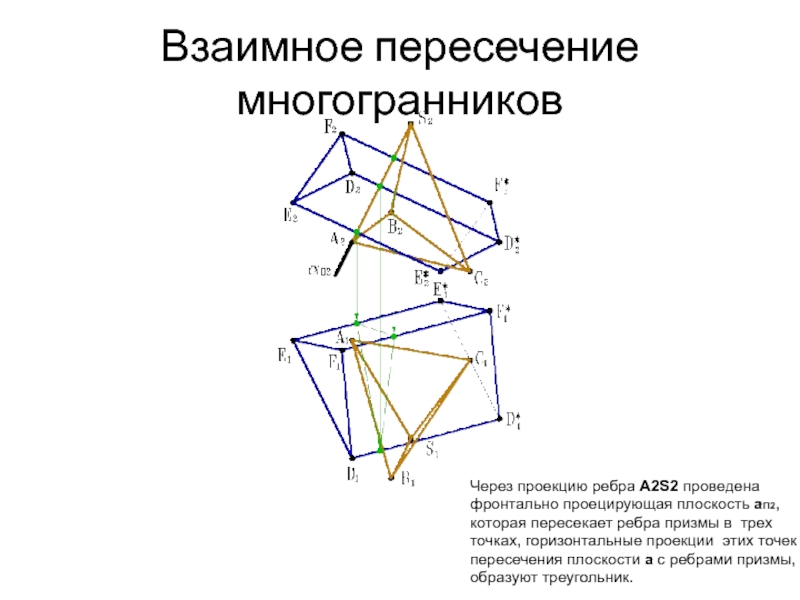
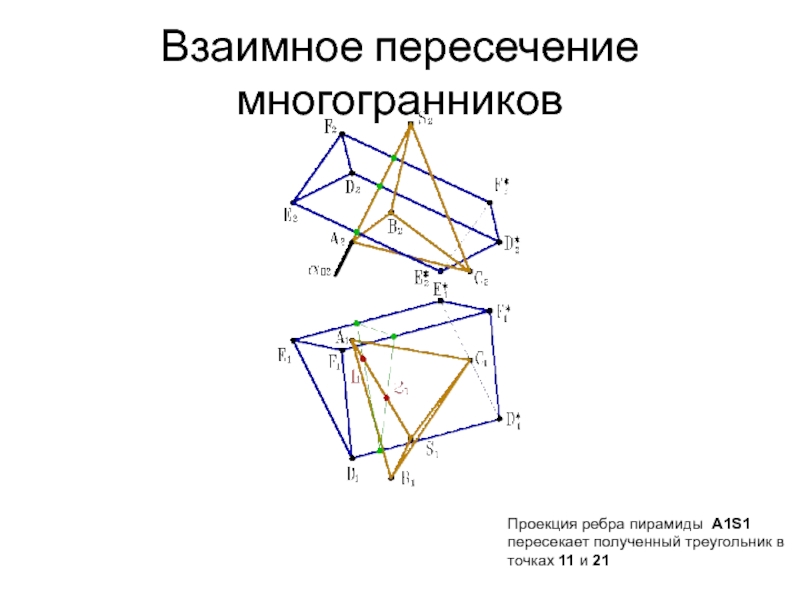
- 30. Взаимное пересечение многогранников Проекция ребра пирамиды A1S1 пересекает полученный треугольник в точках 11 и 21
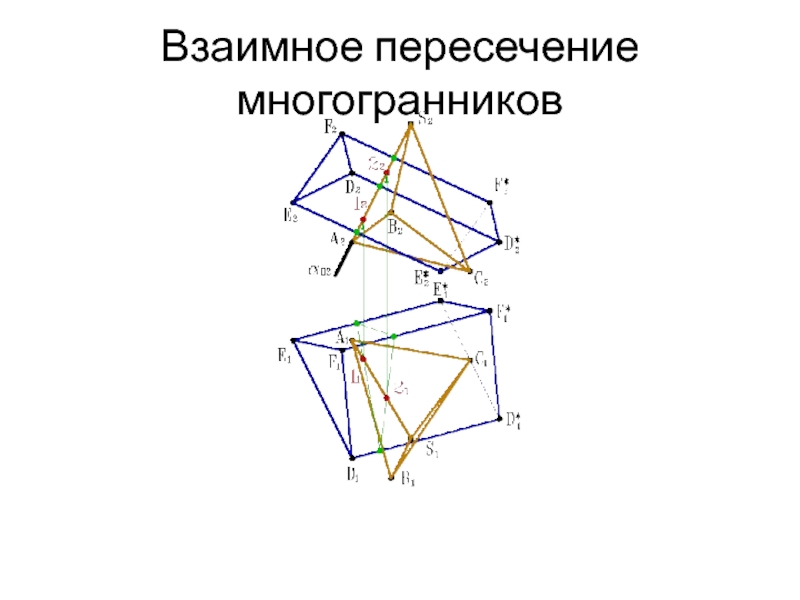
- 31. Взаимное пересечение многогранников
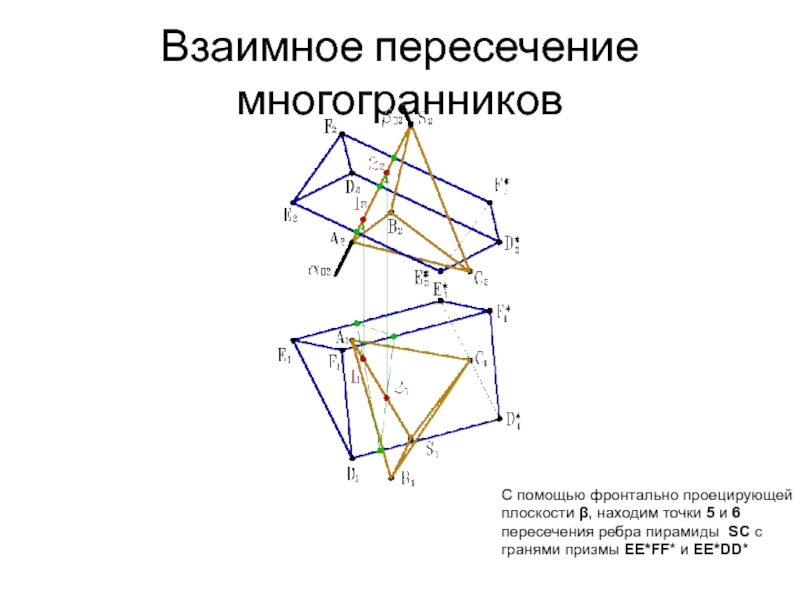
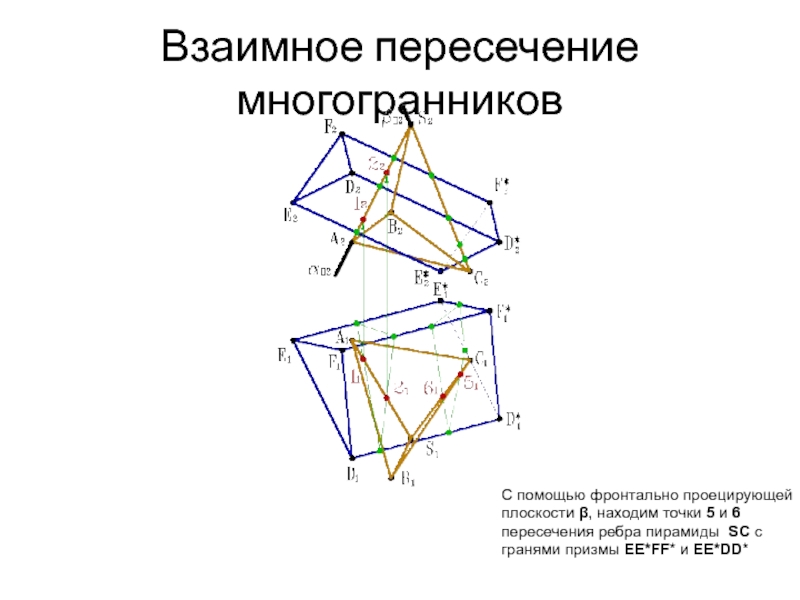
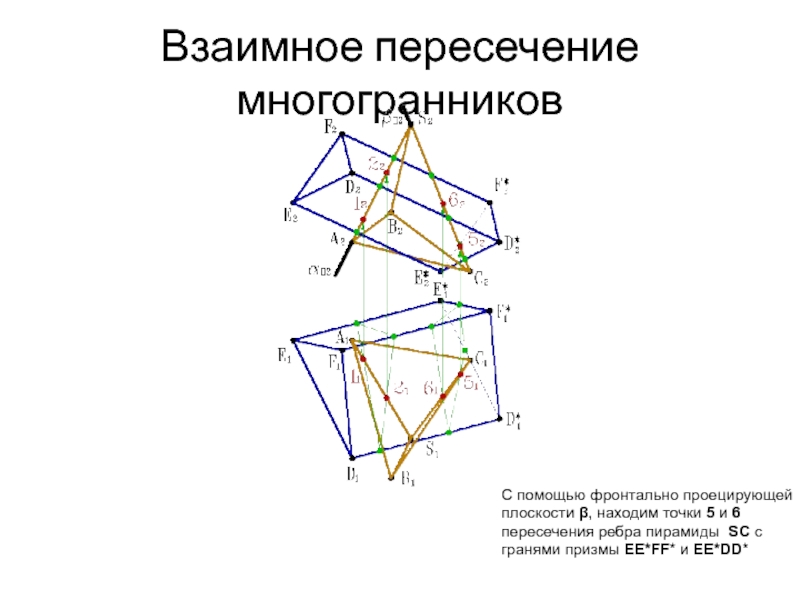
- 32. Взаимное пересечение многогранников С помощью фронтально проецирующей
- 33. Взаимное пересечение многогранников С помощью фронтально проецирующей
- 34. Взаимное пересечение многогранников С помощью фронтально проецирующей
- 35. Взаимное пересечение многогранников С помощью фронтально проецирующей
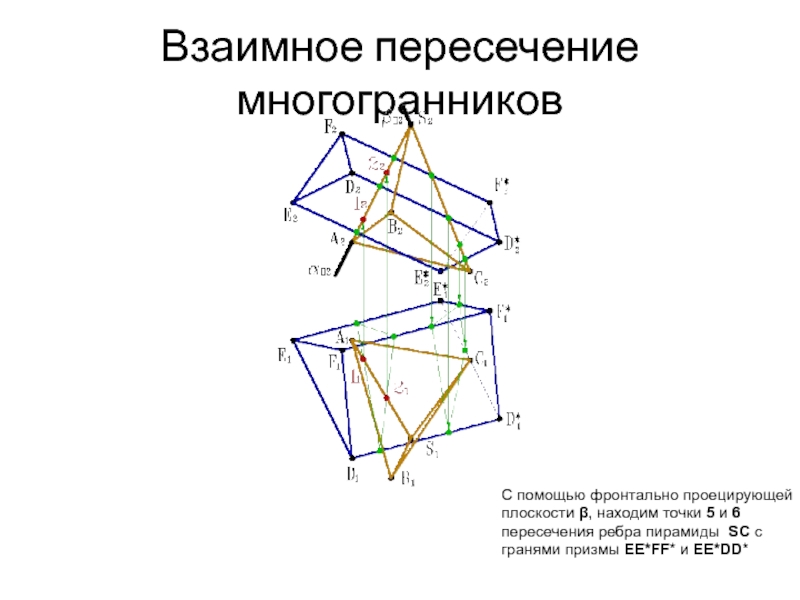
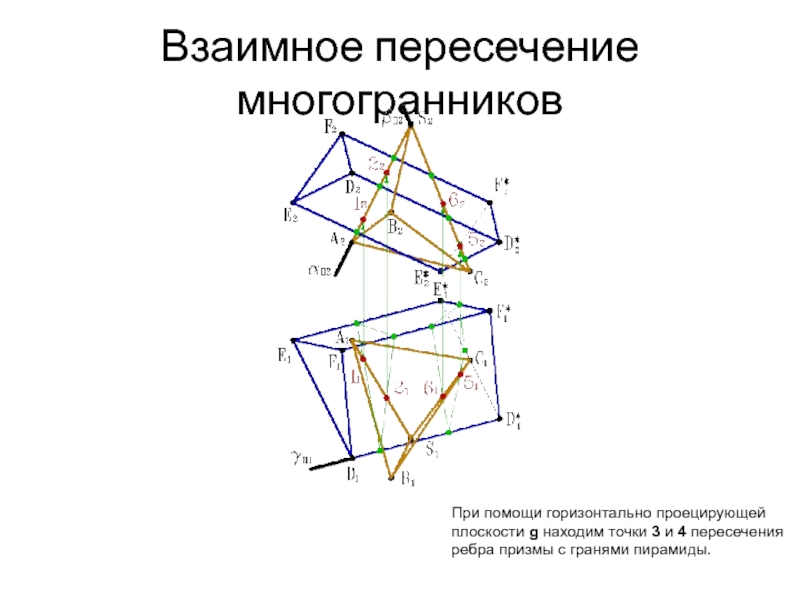
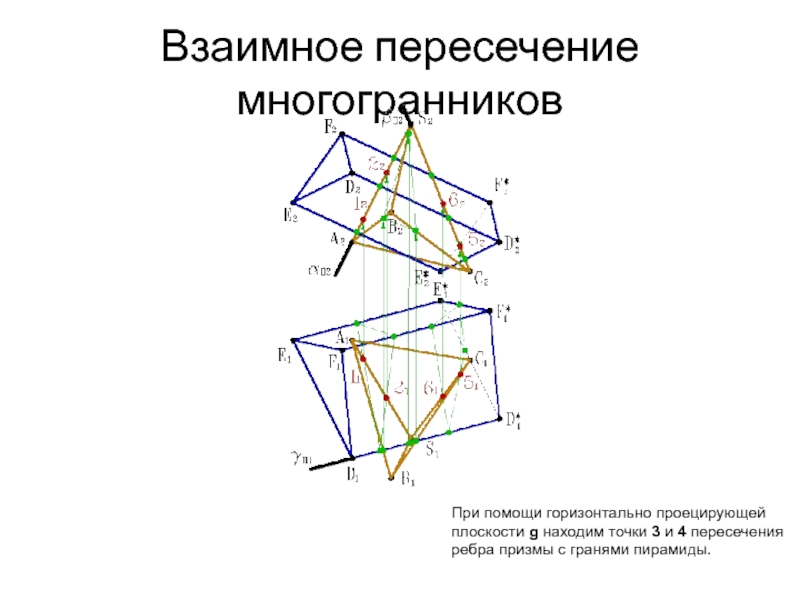
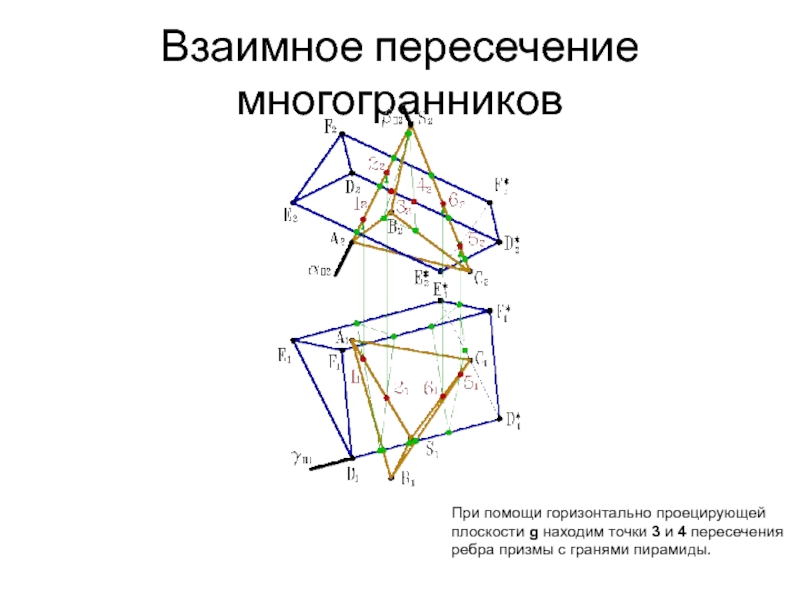
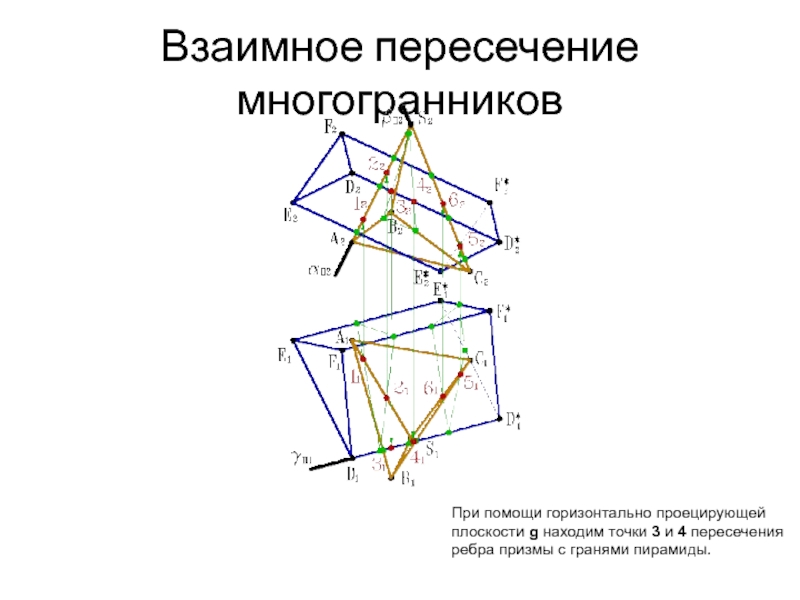
- 36. Взаимное пересечение многогранников При помощи горизонтально проецирующей
- 37. Взаимное пересечение многогранников При помощи горизонтально проецирующей
- 38. Взаимное пересечение многогранников При помощи горизонтально проецирующей
- 39. Взаимное пересечение многогранников При помощи горизонтально проецирующей
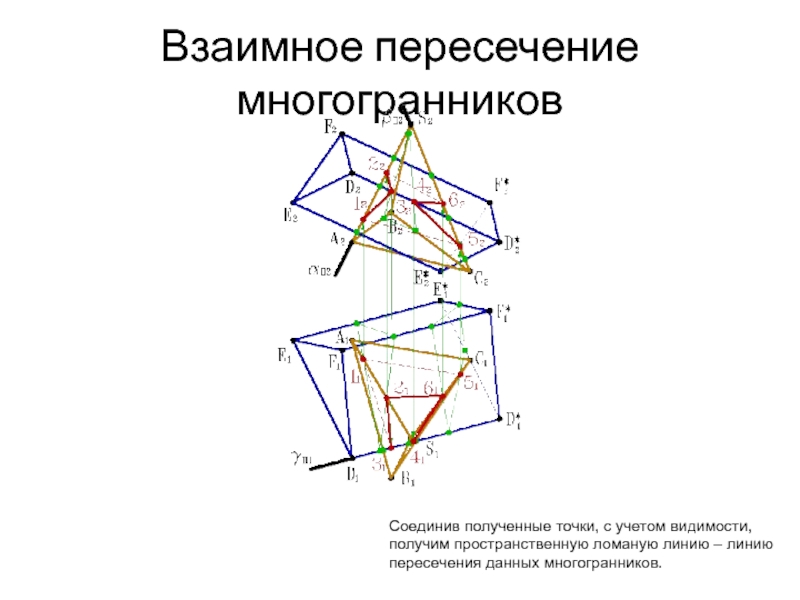
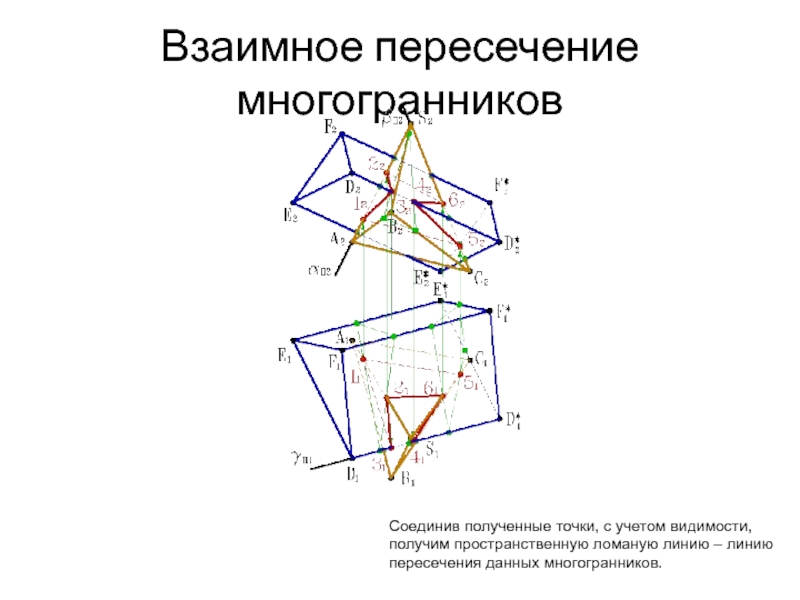
- 40. Взаимное пересечение многогранников Соединив полученные точки, с
- 41. Взаимное пересечение многогранников Соединив полученные точки, с
- 42. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
КАФЕДРА ПРИКЛАДНОЙ И КОМПЬЮТЕРНОЙ
ОПТИКИ
Слайд 2Пересечение плоскости с многогранником
Построение сечения многогранника требует многократного решения задачи
о нахождении точки пересечении прямой с плоскостью. Точки, в которых
ребра многогранника пересекаются с заданной плоскостью, будут вершинами искомого сечения.Тот же результат можно получить, сведя задачу к построению линий пересечения плоскости с гранями тела.
Слайд 3Пересечение плоскости с многогранником
Задача. Дана призма и плоскость общего положения
заданная двумя пересекающимися прямыми а и b (см.рис.). Необходимо построить
сечение призмы данной плоскостью.Слайд 4Пересечение плоскости с многогранником
Для чего, через горизонтальные проекции ребер проведем
вспомогательные секущие плоскости α, β и γ. Построив линии пересечения
вспомогательных плоскостей с заданной, находим на фронтальной проекции точки пересечения их с соответствующими ребрами призмы К2, М2 и N2 – вершины фронтальной проекции сечения призмы. По линиям связи находим горизонтальные проекции этих точек. Полученные точки соединяем прямыми линиями, с учетом видимости. При решении вопроса о видимости сторон построенного сечения следует иметь в виду достаточно очевидное правило: точка и линия, лежащие на поверхности многогранника, видимы только в том случае, если они расположены на видимой грани.Слайд 5Пересечение плоскости с многогранником
Задачу можно решить методом нахождением
точек пересечения
ребер призмы с плоскостью
Слайд 6Пересечение плоскости с многогранником
Через горизонтальные проекции ребер
проведем вспомогательную секущую
плоскость α
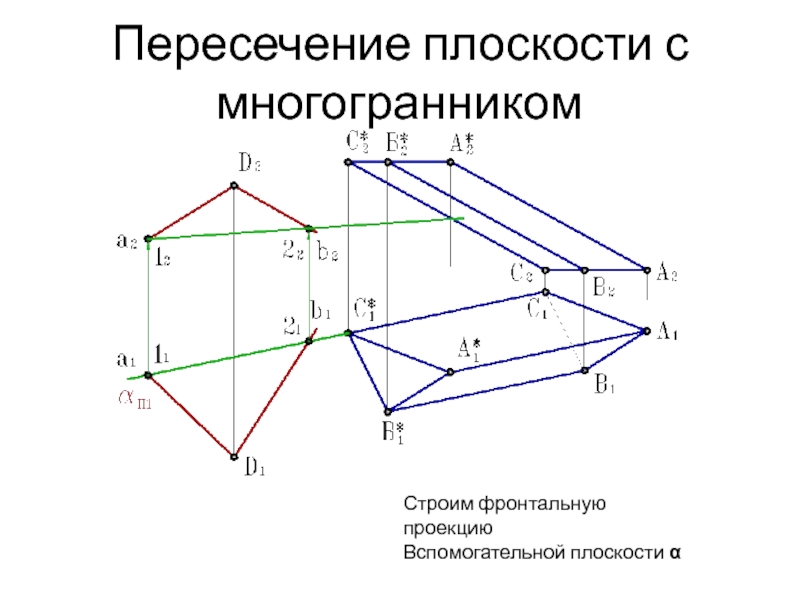
Слайд 7Пересечение плоскости с многогранником
Строим фронтальную проекцию
Вспомогательной плоскости α
Слайд 8Пересечение плоскости с многогранником
Строим фронтальную проекцию
Вспомогательной плоскости α
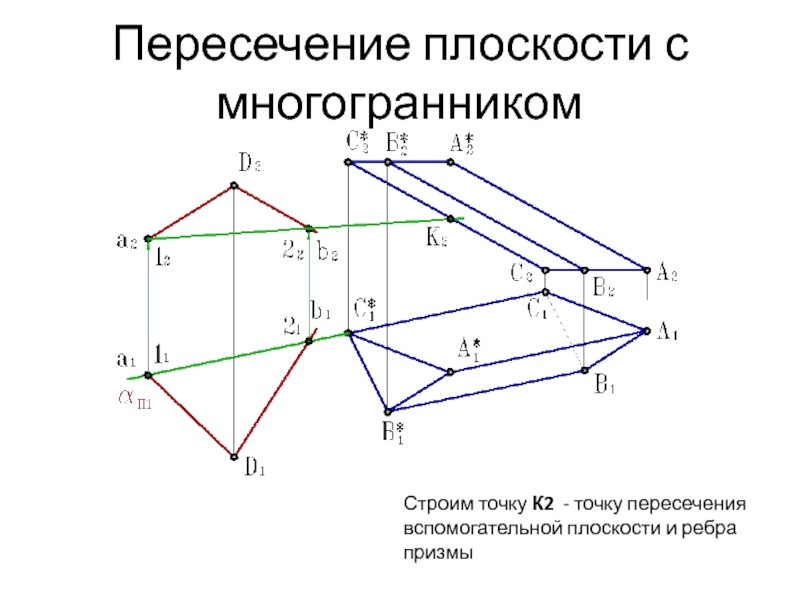
Слайд 9Пересечение плоскости с многогранником
Строим точку К2 - точку пересечения
вспомогательной
плоскости и ребра призмы
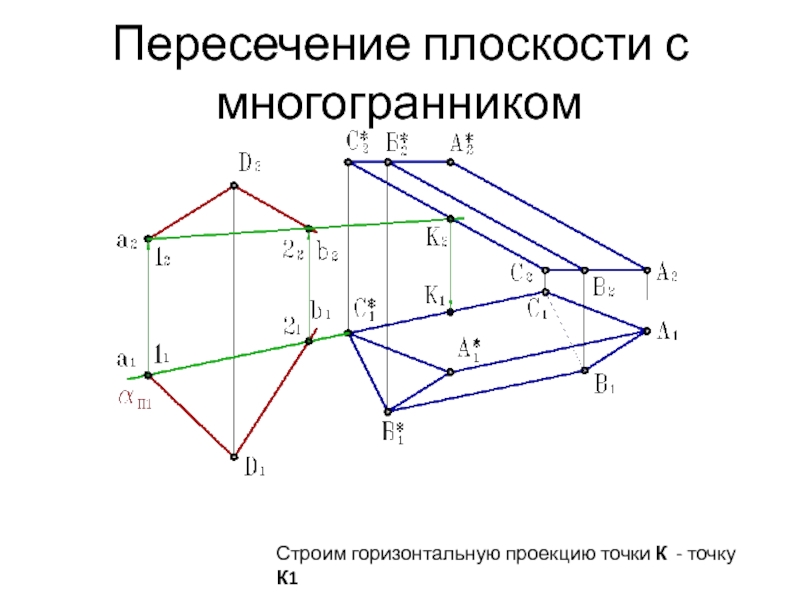
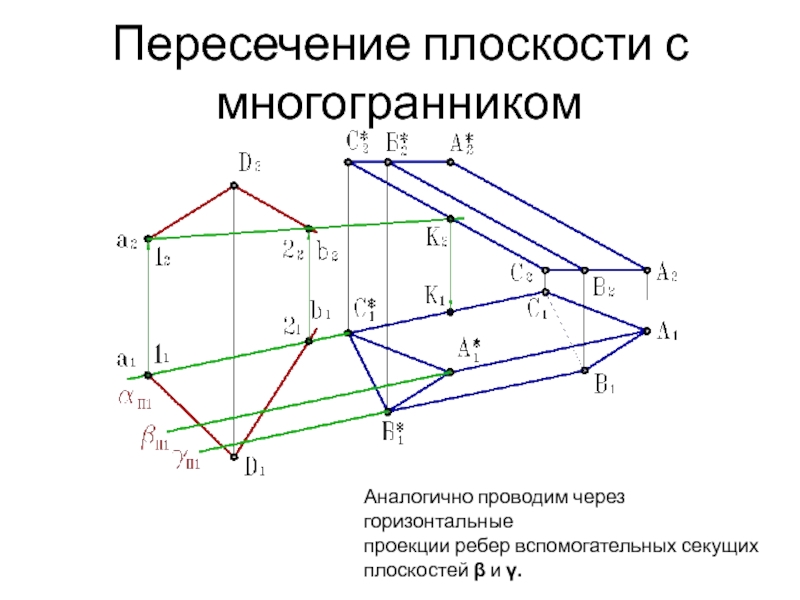
Слайд 11Пересечение плоскости с многогранником
Аналогично проводим через горизонтальные
проекции ребер вспомогательных
секущих
плоскостей β и γ.
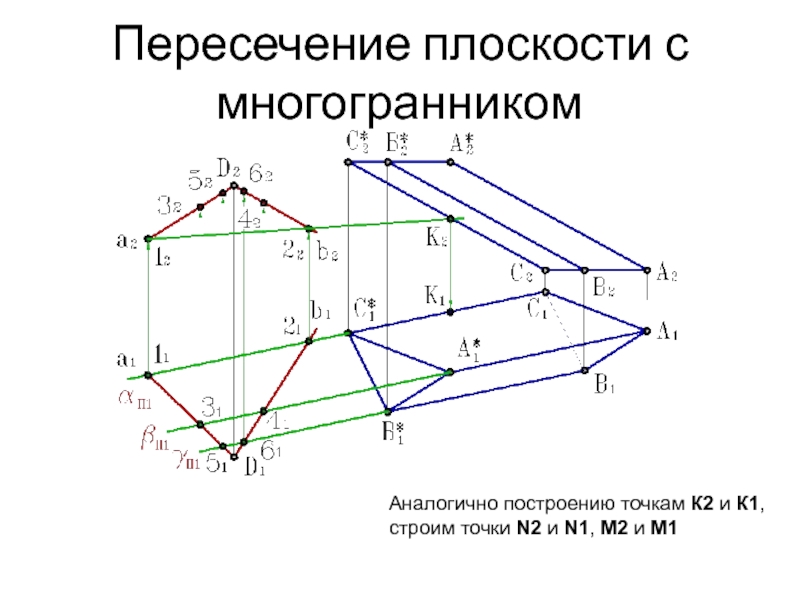
Слайд 12Пересечение плоскости с многогранником
Аналогично построению точкам К2 и К1,
строим
точки N2 и N1, M2 и M1
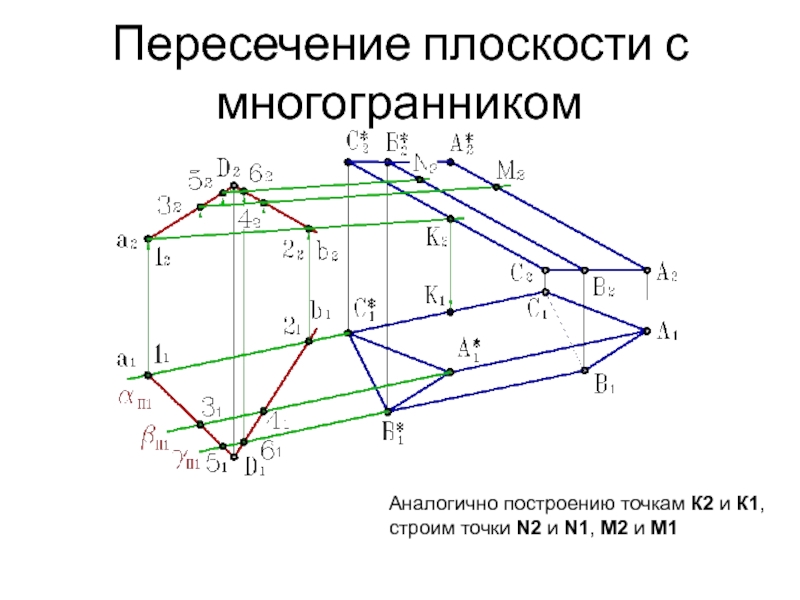
Слайд 13Пересечение плоскости с многогранником
Аналогично построению точкам К2 и К1,
строим
точки N2 и N1, M2 и M1
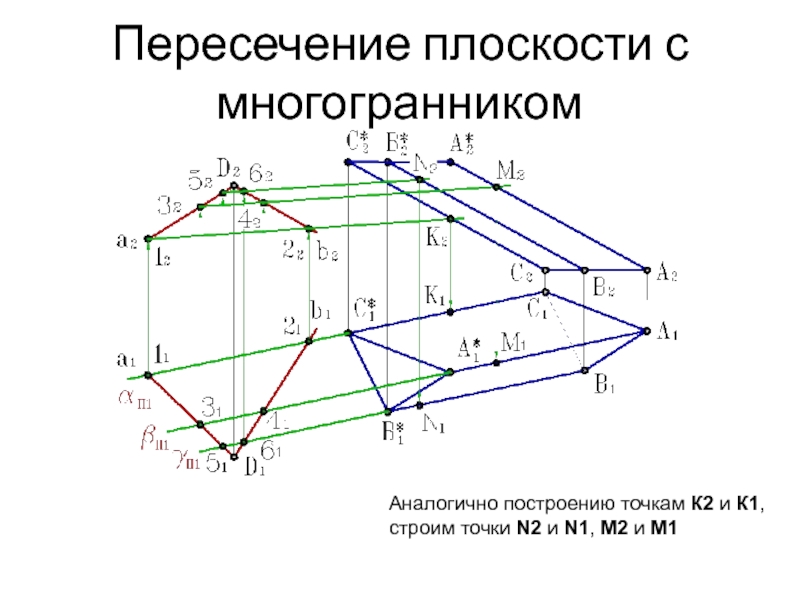
Слайд 14Пересечение плоскости с многогранником
Аналогично построению точкам К2 и К1,
строим
точки N2 и N1, M2 и M1
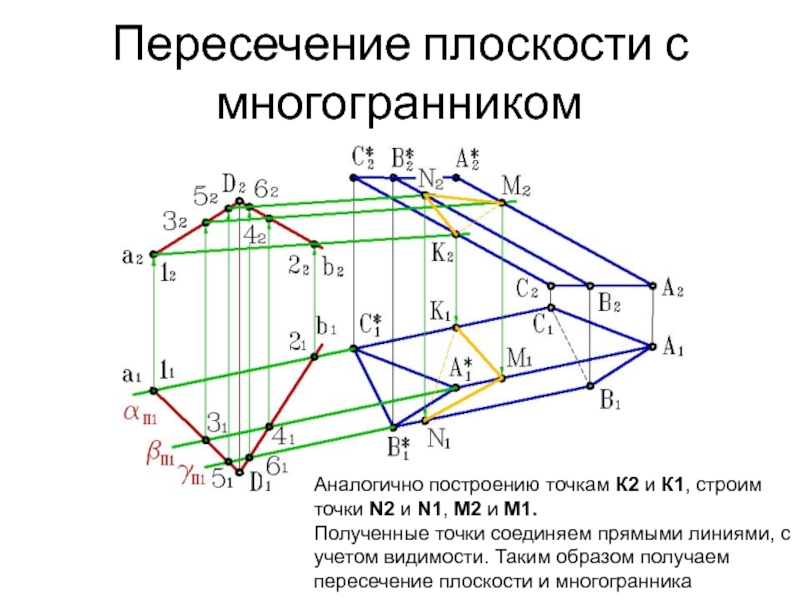
Слайд 15Пересечение плоскости с многогранником
Аналогично построению точкам К2 и К1, строим
точки N2 и N1, M2 и M1.
Полученные точки соединяем
прямыми линиями, с учетом видимости. Таким образом получаем
пересечение плоскости и многогранника
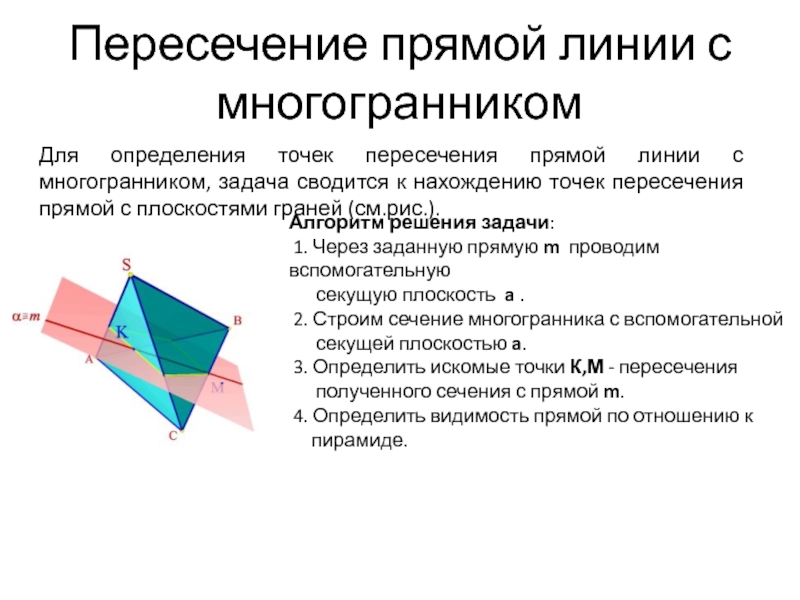
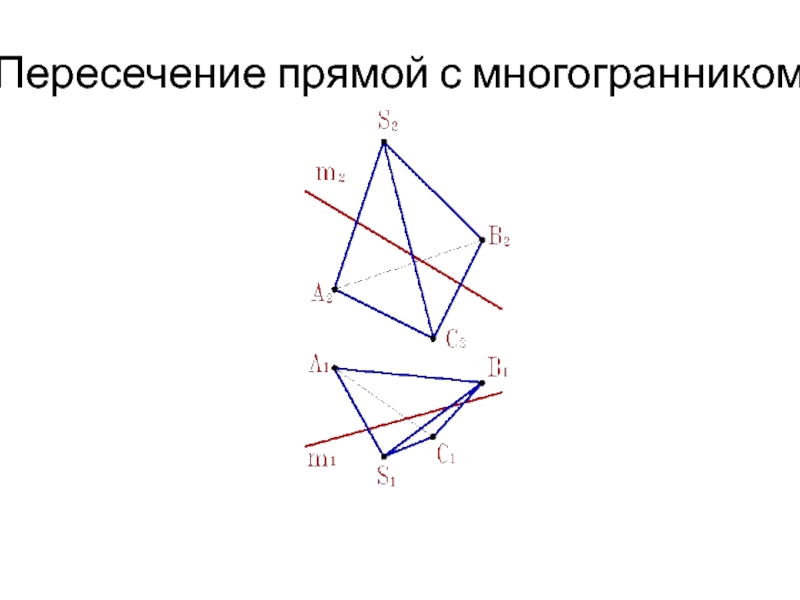
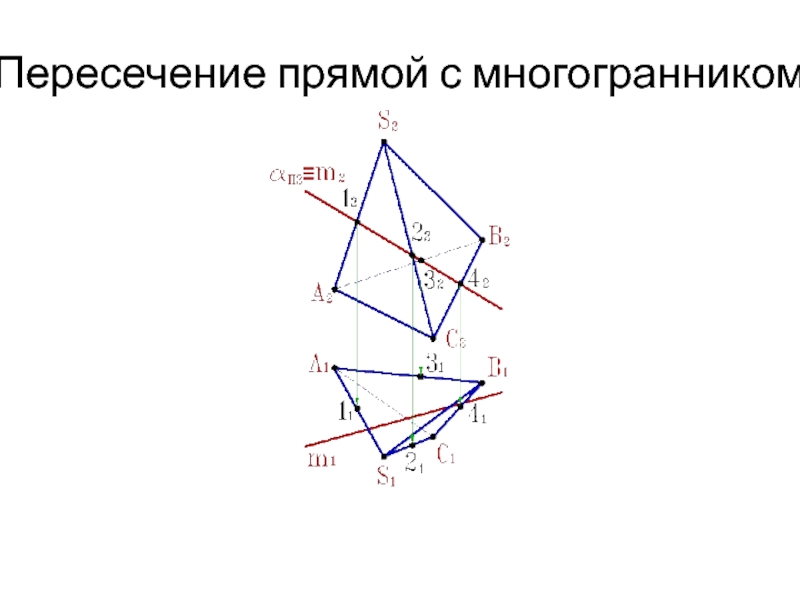
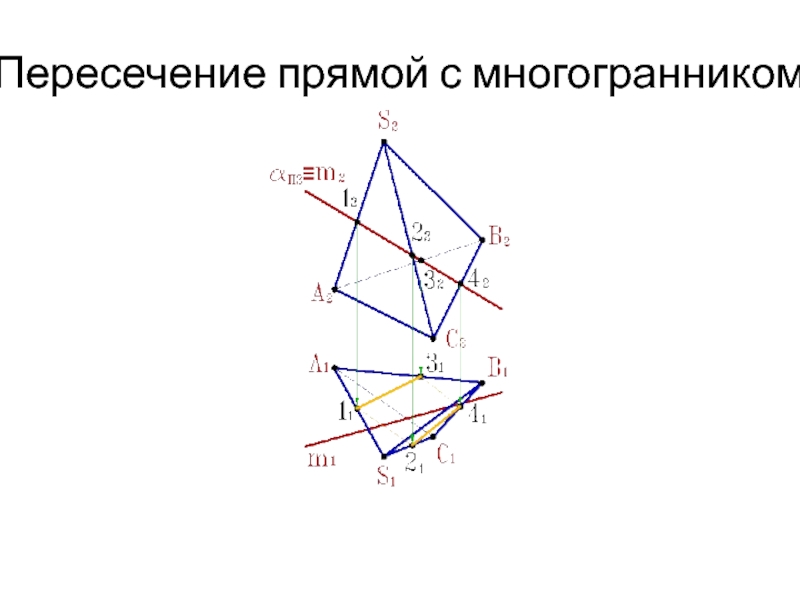
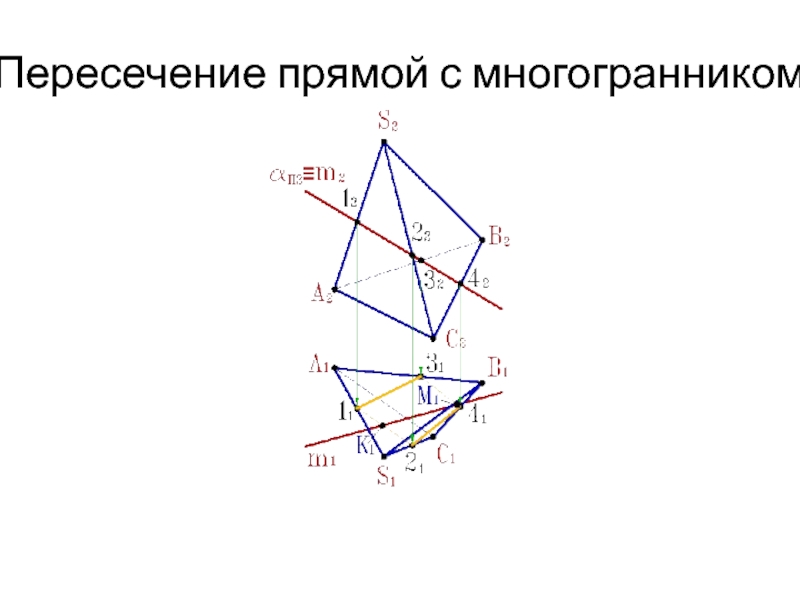
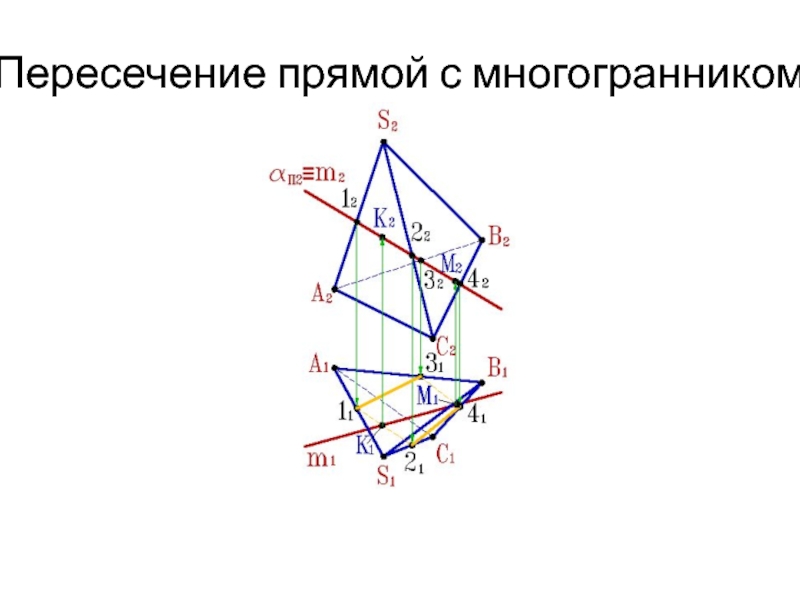
Слайд 16Пересечение прямой линии с многогранником
Для определения точек пересечения прямой линии
с многогранником, задача сводится к нахождению точек пересечения прямой с
плоскостями граней (см.рис.).Алгоритм решения задачи:
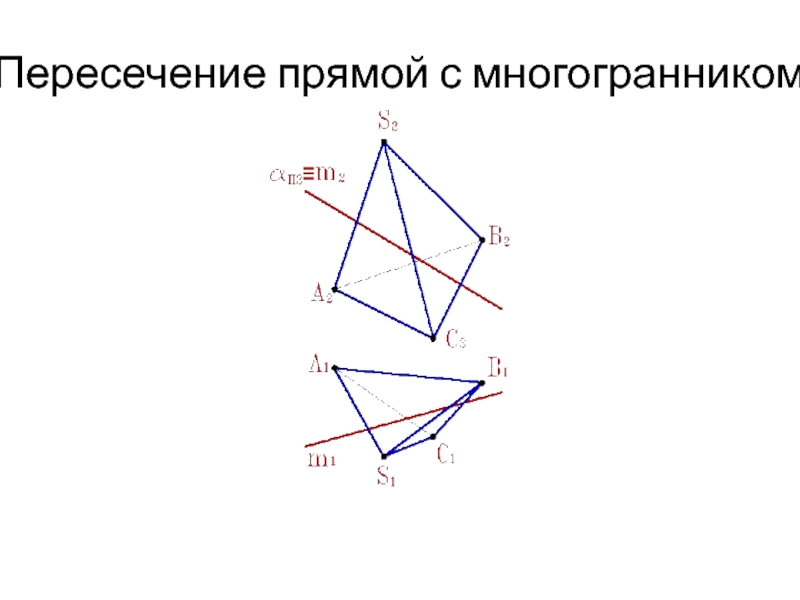
1. Через заданную прямую m проводим вспомогательную
секущую плоскость a .
2. Строим сечение многогранника с вспомогательной
секущей плоскостью a.
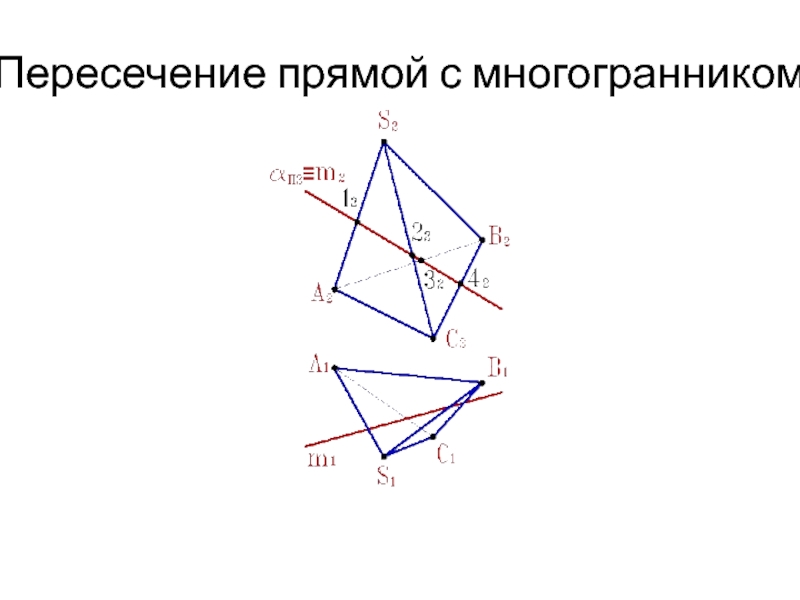
3. Определить искомые точки К,М - пересечения
полученного сечения с прямой m.
4. Определить видимость прямой по отношению к
пирамиде.
Слайд 24Взаимное пересечение многогранников
Построение линии взаимного пересечения многогранных поверхностей можно производить
двумя способами, комбинируя их между собой или выбирая из них
тот, который в зависимости от условий задания дает более простые построения.Слайд 25Взаимное пересечение многогранников.
Способ 1
Определяют точки, в которых ребра одной
из многогранных поверхностей пересекают грани другой и ребра второй пересекают
грани первой (задача на пересечение прямой с плоскостью). Через найденные точки в определенной последовательности проводят ломаную линию, представляющую собой линию пересечения данных многогранников. При этом можно соединять прямыми проекции лишь тех точек, полученных в процессе построения, которые лежат в одной и той же грани.Слайд 26Взаимное пересечение многогранников.
Способ 2
Определяют отрезки прямых, по которым грани
одной поверхности пересекают грани другой (задача на пересечение двух плоскостей
между собой); эти отрезки являются звеньями ломаной линии, получаемой при пересечении многогранных поверхностей.Если проекция ребра одной из поверхностей не пересекает проекции грани другой, хотя бы на одной из проекций, то данное ребро не пересекает этой грани. Однако пересечение проекций ребра и грани еще не означает, что ребро и грань пересекаются в пространстве