Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сечение рассеяния в кулоновском потенциале. Сечение рассеяния в обратноквадратичном потенциале
Содержание
- 1. Сечение рассеяния в кулоновском потенциале. Сечение рассеяния в обратноквадратичном потенциале
- 2. Лекция 3 Слайд 2Кулоновский потенциал взаимодействия U(r) =
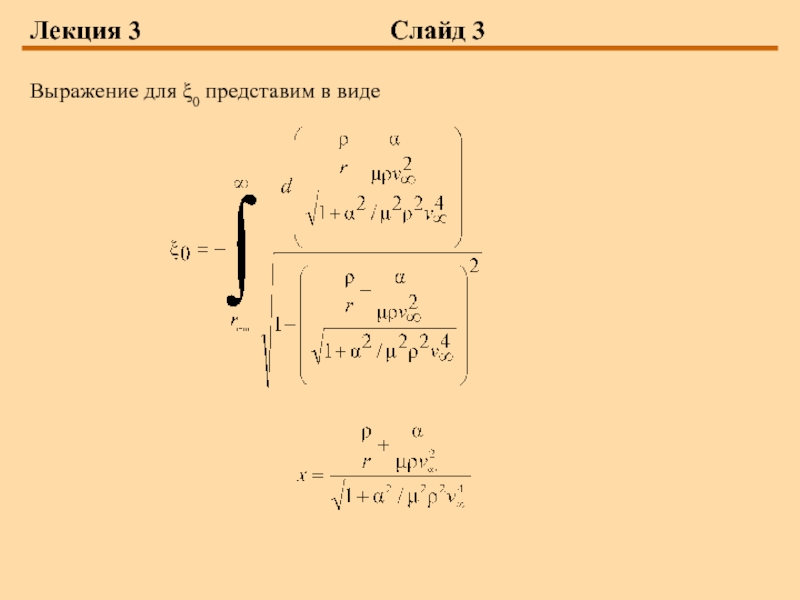
- 3. Лекция 3 Слайд 3Выражение для ξ0 представим в виде
- 4. Лекция 3 Слайд 4получим табличный интегралгде Представив получимТак как ξ0 = (π – χ)/2, то
- 5. Лекция 3 Слайд 5В соответствии с общим определением
- 6. Лекция 3 Слайд 6Для того чтобы выразить sin4(χ)
- 7. Лекция 3 Слайд 7при γ < 1для γ
- 8. Лекция 3 Слайд 8Дифференциальное сечения рассеяния как функция
- 9. Лекция 3 Слайд 9окончательно, имеем При упругом рассеянии
- 10. Лекция 3 Слайд 10
- 11. Лекция 3 Слайд
- 12. Лекция 3 Слайд
- 13. Лекция 3 Слайд
- 14. Скачать презентанцию
Лекция 3 Слайд 2Кулоновский потенциал взаимодействия U(r) = α/r (где α = q1q2) – один из немногих потенциалов, для которого можно вычислить аналитически дифференциальное сечение рассеяния.μ = m1m2/(m1+m2)Решение этого уравнения Одному значению
Слайды и текст этой презентации
Слайд 1Лекция 3 Слайд 1
Темы лекции
Сечение рассеяния в кулоновском потенциале.
Сечение рассеяния в
обратноквадратичном потенциале.
Слайд 2Лекция 3 Слайд 2
Кулоновский потенциал взаимодействия U(r) = α/r (где α
= q1q2) – один из немногих потенциалов, для которого можно
вычислить аналитически дифференциальное сечение рассеяния.μ = m1m2/(m1+m2)
Решение этого уравнения
Одному значению прицельного параметра ρ в общем случае соответствуют два значения rmin.
Слайд 5Лекция 3 Слайд 5
В соответствии с общим определением дифференциального сечения
Так как
2μv∞2 = 4(m1v∞2/2)m2/(m1+m2) = 4E0 /(1+γ), а элемент телесного угла
dω = sinχdχdϕ, тоЭто Резерфордовское дифференциальное сечение рассеяния
в кулоновском потенциале. Оно не зависит от знаков зарядов взаимодейст-вующих частиц. Переход в л.с.к. осуществляется в соответствии с общим правилом.
Слайд 6Лекция 3 Слайд 6
Для того чтобы выразить sin4(χ) через угол θ
воспользуемся тригонометрическим равенством
где оба знака перед корнем соответствуют случаю γ
> 1, при γ < 1 остается только верхний знак.При γ > 1 Резерфордовское дифференциальное сечение рассеяния в лабораторной системе координат имеет вид
Слайд 7Лекция 3 Слайд 7
при γ < 1
для γ
выражение существенно упрощается
Угол рассеяния в л.с.к. θ = 135о.
Как видно
из рисунка, даже при γ = 0,1 использование приближенного
выражения приводит к ошибке ≅ 15%.
γ
Слайд 8Лекция 3 Слайд 8
Дифференциальное сечения рассеяния как функция переданной энергии E2
частице m2 , т.е. dσ(E2)/dE2.
из которых
Подставим полученные выражения в Резерфордовское
дифференциальное сечение рассеяния
Слайд 9Лекция 3 Слайд 9
окончательно, имеем
При упругом рассеянии в кулоновском потенциале
наиболее вероятны
малые углы рассеяния
столкновения с малой передачей энергии
Слайд 11Лекция 3 Слайд 11
Для описания рассеяния
пучка используется понятие дифференциального сечения рассеяния dσ, определяемого следующим образом.
Пусть
dN – число частиц, рассеиваемых в с.ц.м. в единицу времени на углы, лежащие в диапазоне χ ÷ χ + dχ. Дифференциальное сечение рассеяния для однородного по сечению потока частицdσ = dN/j,
где j – плотность потока частиц.
Из данного определения следует, что dσ имеет размерность площади
(в дальнейшем будем использовать см2).
Если связь между χ и ρ взаимно однозначная, то в диапазон углов χ ÷ χ + dχ будут рассеяны только те частицы, у которых прицельные параметры находятся в диапазоне
ρ(χ) ÷ ρ(χ) + dρ(χ).
Слайд 12Лекция 3 Слайд 12
В случае однородного
пучка и сферически симметричного потенциала взаимодействия число таких частиц равно
числу частиц, прошедших через кольцо площадью 2πρdρ. Поэтому dN = j2πρdρ иПолученное выражение определяет дифференциальное сечение рассеяния, проинтегрированное по азимутальному углу ϕ (именно в силу сферической симметричности потенциала в результате интегрирования появился множитель 2π). В дальнейшем нам будет необходимо дифференциальное сечение рассеяния в единицу телесного угла dω = sinχdχdϕ, которое имеет вид
Слайд 13Лекция 3 Слайд 13
Переход от дифференциального
сечение рассеяния в единицу телесного угла dω в с.ц.м. к
дифференциальному сечению рассеяния в единицу телесного угла dΩ в л.с.к.следует из равенства потоков рассеянных частиц в с.ц.м. и л.с.к. Представив dω = sinχdχdϕ и dΩ = sinθdθdϕ, получим следующее соотношение