Слайд 2Хендрик Антон Лоренц
Лоренц ввел в электродинамику представления о
дискретности электрических зарядов и записал уравнения для электромагнитного поля, созданного
отдельными заряженными частицами (уравнения Максвелла – Лоренца); ввел выражение для силы, действующей на движущийся заряд в электромагнитном поле; создал классическую теорию дисперсии света и объяснил расщепление спектральных линий в магнитном поле (эффект Зеемана). Его работы по электродинамике движущихся сред послужили основой для создания специальной теории относительности.
(1853 – 1928 г.г.)
великий
нидерландский
физик – теоретик,
создатель
классической
электронной
теории
Слайд 3Сила Лоренца – сила, действующая на движущуюся заряженную частицу со
стороны магнитного поля.
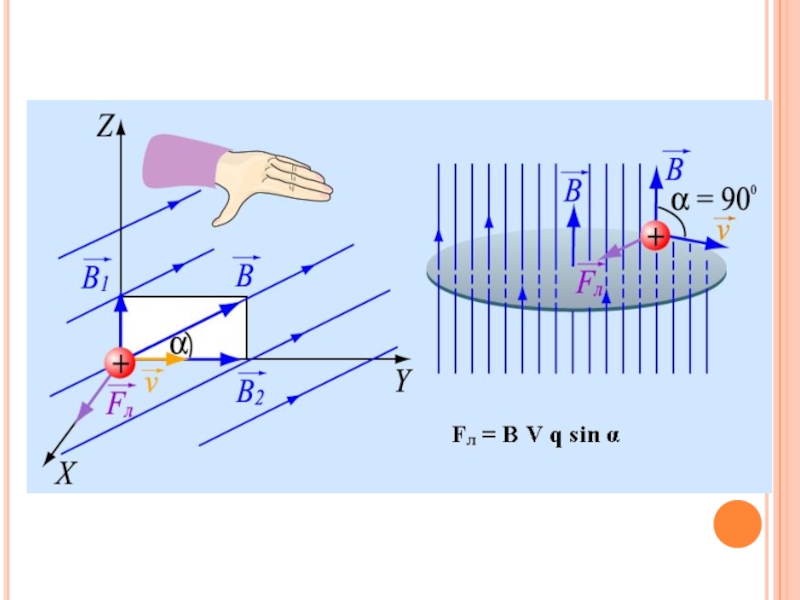
Сила Лоренца вычисляется по формуле:
Fл = qvBsinα ,где
α - угол между скоростью заряженной частицы и вектором магнитной индукции
Слайд 4Сила Лоренца перпендикулярна векторам V и B, направление определяется правилом
левой руки: если левую руку расположить так, что четыре вытянутых
пальца указывают направление скорости положительного заряда(или противоположны скорости отрицательного заряда), а вектор магнитной индукции входит в ладонь, то отогнутый (в плоскости ладони) на 90° большой палец покажет направление силы, действующей на данный заряд.
Слайд 6В- вектор магнитной индукции;
q – заряд , на который оказывается
воздействие;
v – скорость частицы;
Fл – сила Лоренца
Слайд 7Траектория движения заряженной частицы в однородном магнитном поле зависит от
угла α.
Рассмотрим 2 частных случая:
1. Заряженная частица влетает в магнитное
поле
параллельно линиям магнитной индукции => v //b
В этом случае α = 0, sin α = 0, Fл = 0. В отсутствии
силы Лоренца частица будет продолжаться
двигаться равномерно и прямолинейно с начальной
скоростью.
2. Заряженная частица влетает в магнитное поле со
скоростью v, перпендикулярно линиям магнитной
индукции. В этом случае α = 90°, sin α = 1, Fл =qvB.
Сила Лоренца перпендикулярна скорости, поэтому
модуль скорости частицы не изменяется, но
изменяется ее направление. Сила Лоренца заставляет
частицу все время двигаться по окружности.
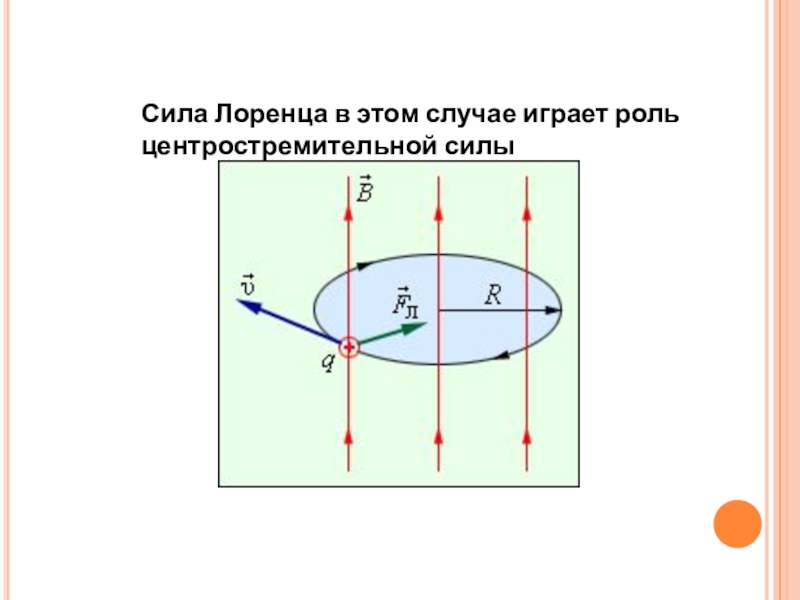
Слайд 8Сила Лоренца в этом случае играет роль центростремительной силы
Слайд 9При движении заряженной частицы в магнитном поле сила Лоренца работы
не совершает. Поэтому модуль вектора скорости при движении частицы не
изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору то частица будет двигаться по окружности радиуса
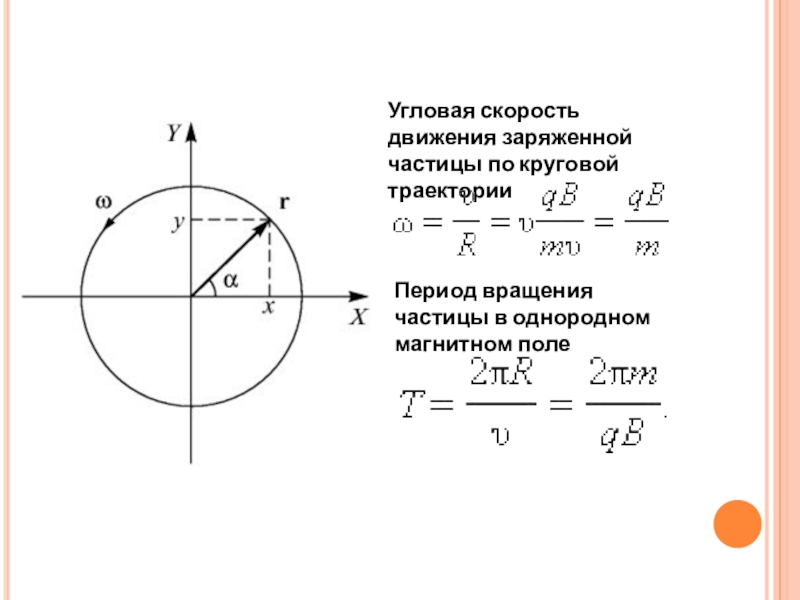
Слайд 10Угловая скорость движения заряженной частицы по круговой траектории
Период вращения
частицы в однородном магнитном поле
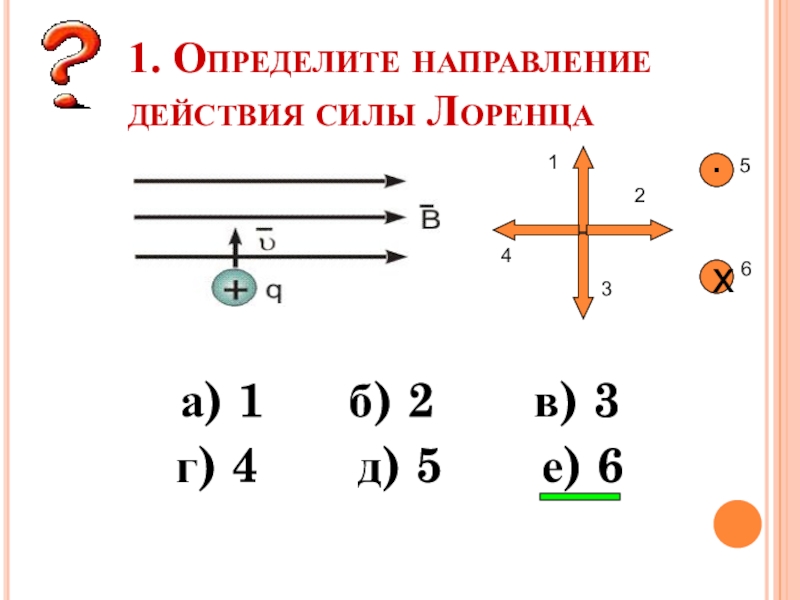
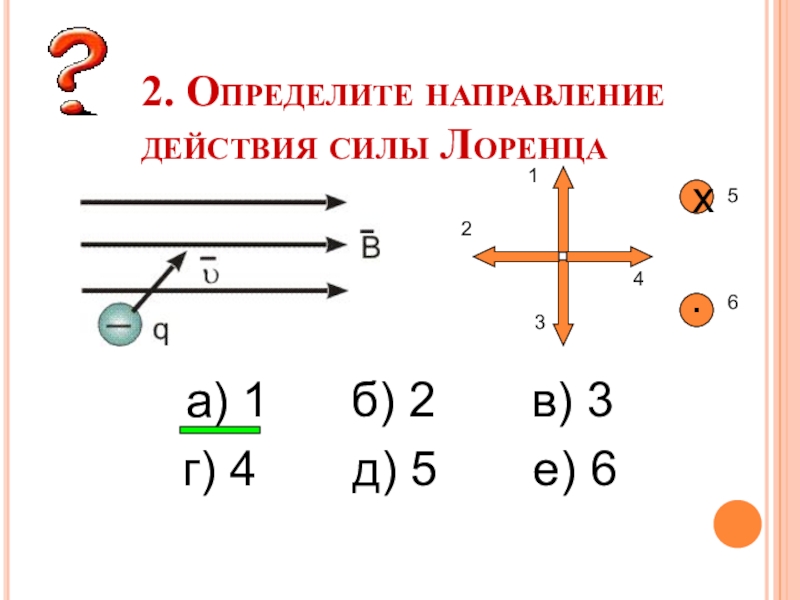
Слайд 111. Определите направление действия силы Лоренца
а) 1 б)
2 в) 3
г)
4 д) 5 е) 6
х
▪
1
2
3
4
5
6
Слайд 122. Определите направление действия силы Лоренца
▪
х
1
2
3
4
5
6
а) 1 б)
2 в) 3
г)
4 д) 5 е) 6
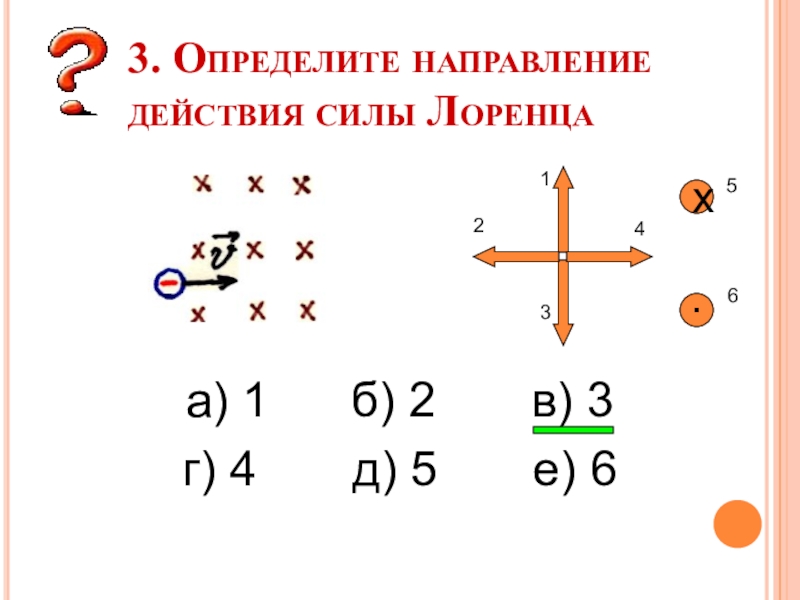
Слайд 133. Определите направление действия силы Лоренца
а) 1 б)
2 в) 3
г)
4 д) 5 е) 6
х
▪
1
2
3
4
5
6
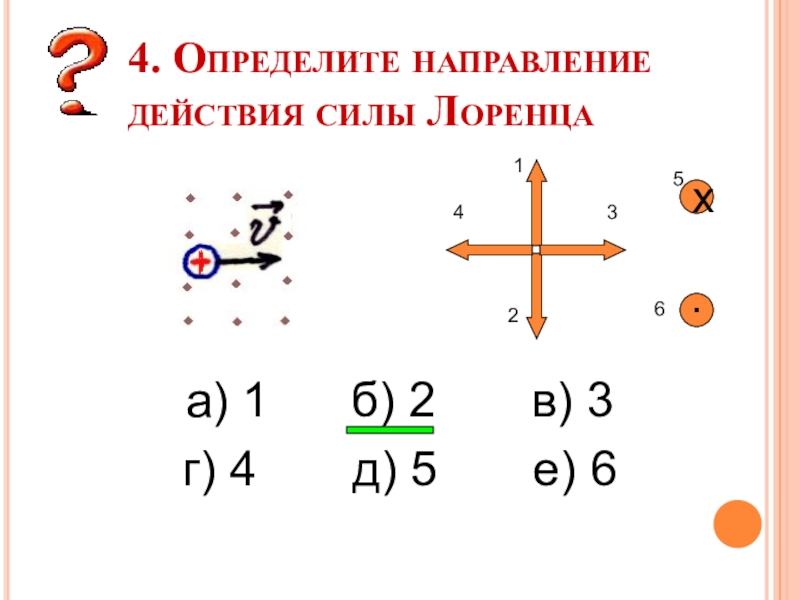
Слайд 144. Определите направление действия силы Лоренца
а) 1 б)
2 в) 3
г)
4 д) 5 е) 6
х
▪
1
3
2
4
5
6
Слайд 15В однородном магнитном поле, индукция которого
протон движется перпендикулярно вектору магнитной
индукции В по окружности радиусом 5 м. Определите скорость протона.
Электрон влетает в однородное магнитное поле с индукцией перпендикулярно линиям индукции этого поля и движется по окружности радиуса Вычислите скорость электрона.
В однородном магнитном поле с индукцией протон движется перпендикулярно вектору индукции со скоростью Определите радиус траектории протона.
Слайд 17Угловая скорость движения заряженной частицы по круговой траектории называется циклотронной
частотой. Циклотронная частота не зависит от скорости (следовательно, и от
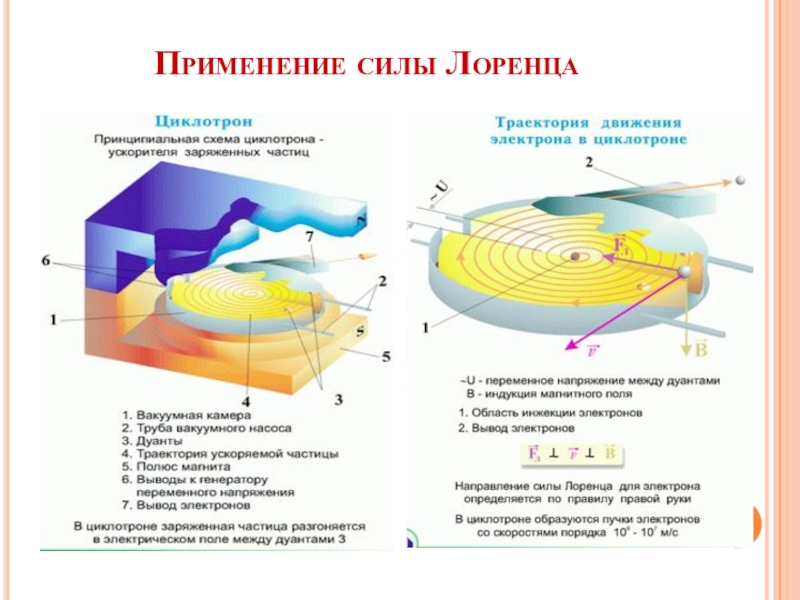
кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис.
Движение заряженных частиц в вакуумной камере циклотрона.
Слайд 18Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся
два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам
приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Слайд 19Однородные магнитные поля используются во многих приборах и, в частности,
в масс-спектрометрах – устройствах, с помощью которых можно измерять массы
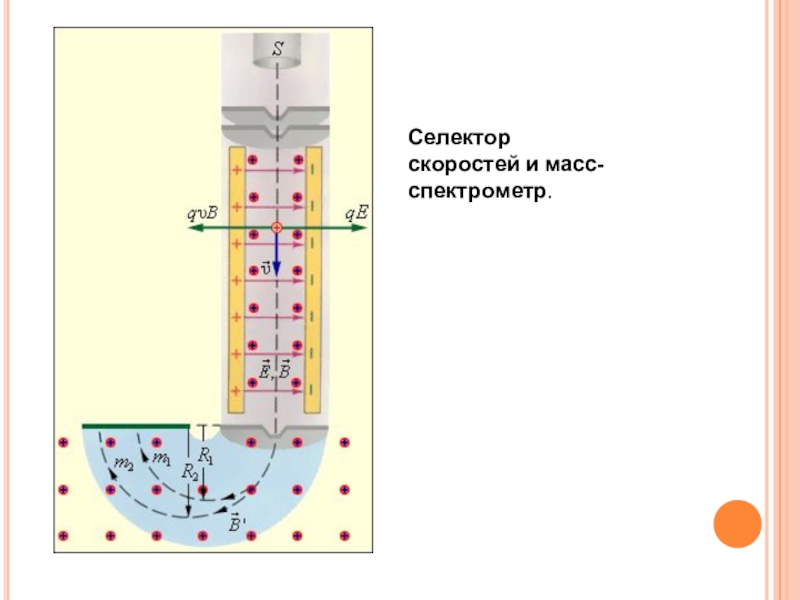
заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита.
Слайд 20На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют
электрическая сила и магнитная сила Лоренца. При условии E = υB эти
силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле. Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB'. Измеряя радиусы траекторий при известных значениях υ и B' можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Слайд 21Селектор скоростей и масс-спектрометр.
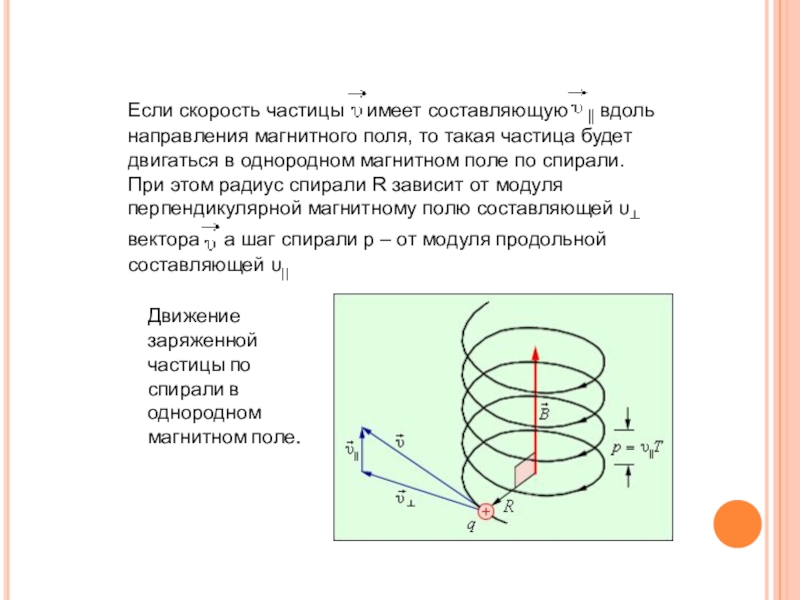
Слайд 22Если скорость частицы имеет составляющую вдоль направления
магнитного поля, то такая частица будет двигаться в однородном магнитном
поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора а шаг спирали p – от модуля продольной составляющей υ||
Движение заряженной частицы по спирали в однородном магнитном поле.
Слайд 23Особенности движения частиц в неоднородном магнитном поле. В неоднородном магнитном
поле индукция поля изменяется в пространстве как по величине, так
и по направлению. В качестве примера рассмотрим магнитное поле, созданное двумя витками с токами, протекающими в одном направлении – магнитную ловушку.
Магнитные ловушки - конфигурации магнитного поля, способные длительное время удерживать заряженные частицы внутри определённого объёма пространства.
Слайд 24Для того чтобы быть магнитной ловушкой, магнитное поле должно удовлетворять
определённым условиям:
заряженные частицы должны иметь скорость;
размеры магн. ловушки должны
быть велики по сравнению с Rл, иначе частица выйдет за пределы ловушки;
увеличение напряжённости магнитного поля.
Слайд 25тороидальные
зеркальные
Один из способов предотвращения ухода частиц из магнитных ловушек вдоль
направления поля состоит в придании ловушке конфигурации, при которой у
объёма, занимаемого ею, вообще нет «концов»
Магнитные ловушки
Другой метод удержания частиц в магнитной ловушке в продольном (по полю) направлении был предложен в 1952 сов. физиком Г. И. Будкером Он состоит в использовании магнитных пробок, или магнитных зеркал, — областей, в которых напряжённость магнитного поля сильно (но плавно) возрастает. Такие области могут отражать «падающие» на них вдоль силовых линий поля заряженные частицы.
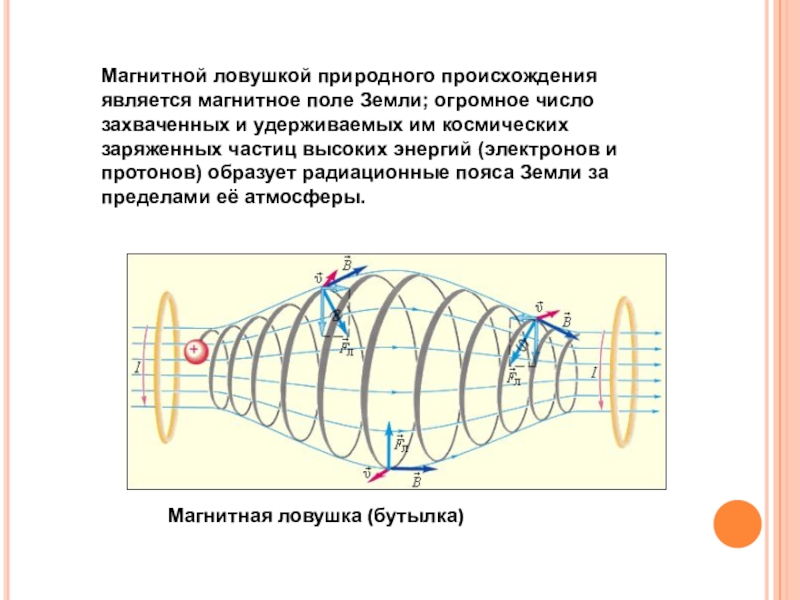
Слайд 26Магнитной ловушкой природного происхождения является магнитное поле Земли; огромное число
захваченных и удерживаемых им космических заряженных частиц высоких энергий (электронов
и протонов) образует радиационные пояса Земли за пределами её атмосферы.
Магнитная ловушка (бутылка)
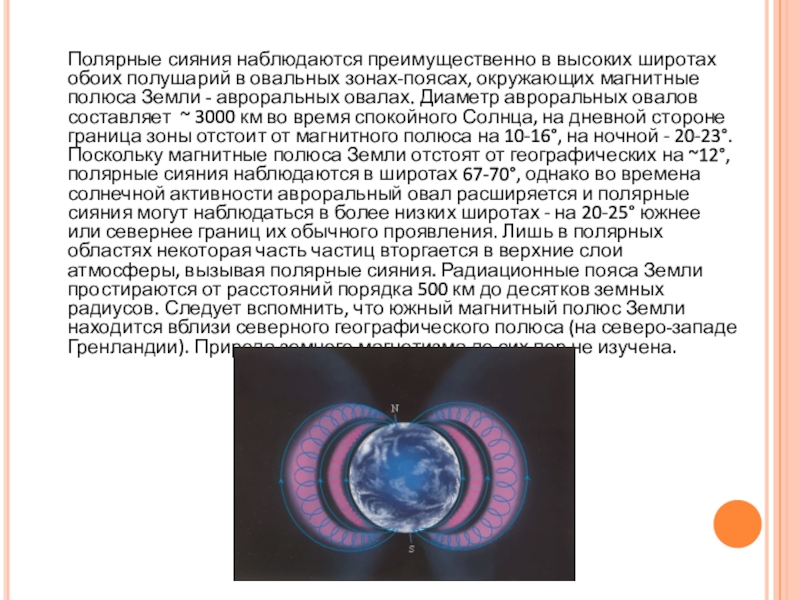
Слайд 27Полярные сияния наблюдаются преимущественно в высоких широтах обоих полушарий в
овальных зонах-поясах, окружающих магнитные полюса Земли - авроральных овалах. Диаметр
авроральных овалов составляет ~ 3000 км во время спокойного Солнца, на дневной стороне граница зоны отстоит от магнитного полюса на 10-16°, на ночной - 20-23°. Поскольку магнитные полюса Земли отстоят от географических на ~12°, полярные сияния наблюдаются в широтах 67-70°, однако во времена солнечной активности авроральный овал расширяется и полярные сияния могут наблюдаться в более низких широтах - на 20-25° южнее или севернее границ их обычного проявления. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.
Слайд 28При столкновении высокоэнергетических частиц солнечного ветра с верхней атмосферой происходит
ионизация и возбуждение атомов и молекул газов, входящих в её
состав. Излучение возбуждённых атомов и наблюдается как полярное сияние. Спектры полярных сияний зависят от состава атмосфер планет: так, например, если для Земли наиболее яркими являются линии излучения возбуждённых кислорода и азота в видимом диапазоне, то для Юпитера — линии излучения водорода в ультрафиолете.
Поскольку ионизация заряженными частицами происходит наиболее эффективно в конце пути частицы и плотность атмосферы падает с высотой в соответствии с барометрической формулой, то высота появлений полярных сияний достаточно сильно зависит от параметров атмосферы планеты, так, для Земли с её достаточно сложным составом атмосферы красное свечение кислорода наблюдается на высотах 200-400 км, а совместное свечение азота и кислорода — на высоте ~110 км. Кроме того, эти факторы обуславливают и форму полярных сияний — размытая верхняя и достаточно резкая нижняя границы.
Слайд 29При наблюдении с поверхности Земли Полярное сияние проявляется в виде
общего быстро меняющегося свечения неба или движущихся лучей, полос, корон,
«занавесей». Длительность полярных сияний составляет от десятков минут до нескольких суток.