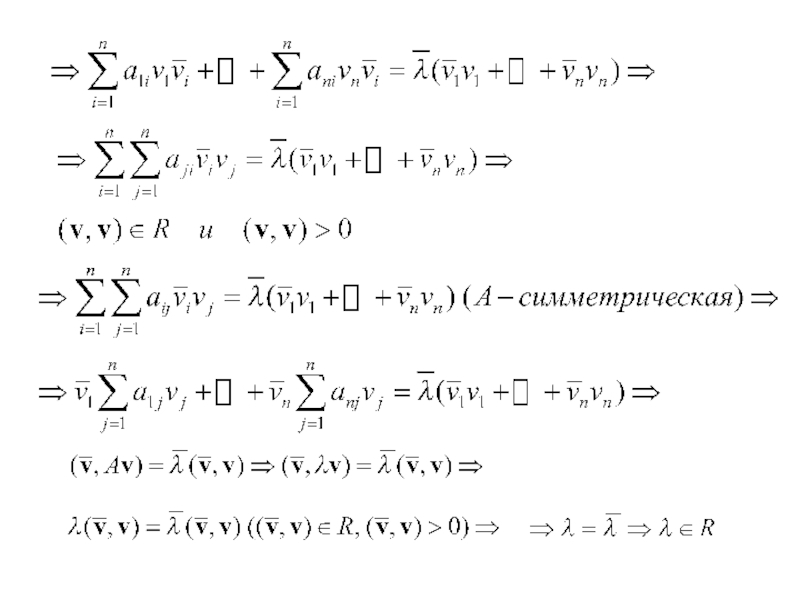Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
симметрич оператор
Содержание
- 1. симметрич оператор
- 2. 1. Симметрическая матрицаОпределение 1.1. Действительная матрица A
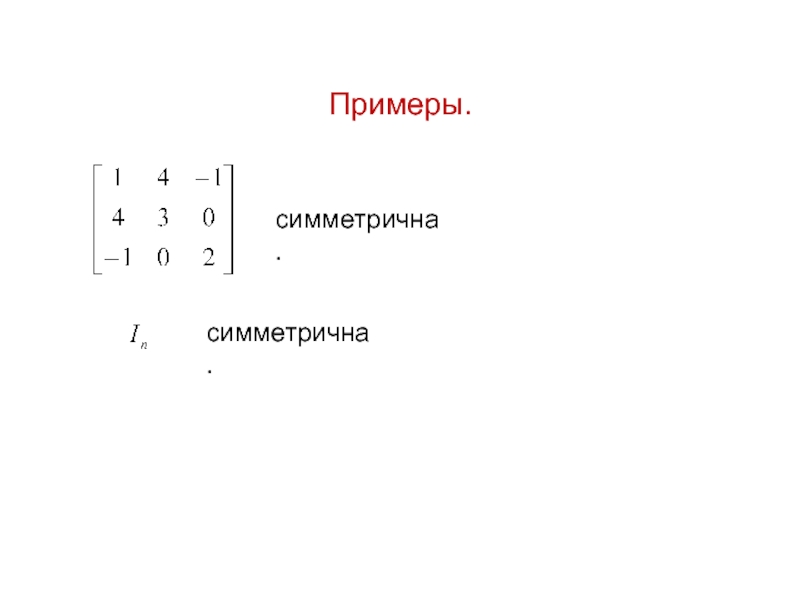
- 3. Примеры.симметрична. симметрична.
- 4. Теорема 1.2. Пусть A – симметрическая матрица,
- 5. Слайд 5
- 6. 2. Пусть v – комплексный собственный вектор
- 7. 2. Симметрический операторОпределение 2.1. Линейный оператор
- 8. Теорема 2.2. Линейный оператор в евклидовом пространстве
- 9. . Пусть
- 10. . Следствие2.3. (1) Все собственные значения симметрического
- 11. Теорема 2.4. Собственные векторы симметрического линейного оператора, соответствующие различным собственным значениям, ортогональны. Доказательство. Пусть Тогда
- 12. Теорема 2.5. Для любого симметрического линейного оператора
- 13. Перейдем к пространству Е размерности n. Пусть
- 14. Следствие 2.6. Матрица симметрического линейного оператора с
- 15. Слайд 15
- 16. Шаг2. Нахождение СВ
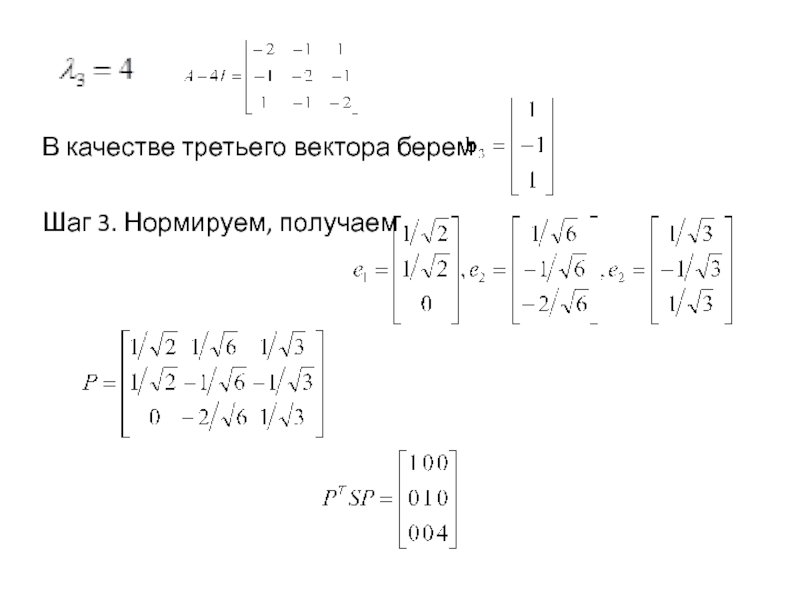
- 17. В качестве третьего вектора беремШаг 3. Нормируем, получаем
- 18. Скачать презентанцию
1. Симметрическая матрицаОпределение 1.1. Действительная матрица A называется симметрической, если Из определения следует, что симметрическая матрица – квадратная матрица.Элементы матрицы симметричны относительно главной диагонали
Слайды и текст этой презентации
Слайд 21. Симметрическая матрица
Определение 1.1. Действительная матрица A называется симметрической, если
Слайд 4Теорема 1.2. Пусть A – симметрическая матрица, тогда все собственные
значения этой матрицы – действительные числа. Для каждого собственного значения
матрицы найдется собственный вектор с действительными координатами.Доказательство (от противного).
1. Пусть v – собственный вектор матрицы А, отвечающий собственному значению λ: А v = λ v . Предположим, что λ – комплексное число.
Перейдем к сопряженным числам:
Умножим скалярно на v:
Слайд 62. Пусть v – комплексный собственный вектор матрицы А, отвечающий
действительному собственному значению λ:
А v = λ
v . Перейдем к сопряженным числам:
Тогда
и - действительный собственный вектор.
QED
Слайд 72. Симметрический оператор
Определение 2.1. Линейный оператор евклидова пространства
Е называется симметрическим, если для любых векторов
выполняетсяСлайд 8Теорема 2.2. Линейный оператор в евклидовом пространстве является симметрическим тогда
и только тогда, когда его матрица в произвольном ортонормированном базисе
симметрична. Доказательство.
Пусть - произвольный ортонормированный базис,
А – матрица оператора.
Тогда
С другой стороны,
Слайд 9.
Пусть
- произвольный ортонормированный базис,
А – симметрическая матрица оператора , u,v – два произвольных вектора евклидова пространства и
Тогда
С другой стороны,
QED
Слайд 10.
Следствие2.3.
(1) Все собственные значения симметрического оператора –
действительные числа.
(2) Любой симметрический оператор имеет хотя бы одно собственное
значение.Слайд 11Теорема 2.4. Собственные векторы симметрического линейного оператора, соответствующие различным собственным
значениям, ортогональны.
Доказательство. Пусть
Тогда
Слайд 12
Теорема 2.5. Для любого симметрического линейного оператора евклидова пространства существует
ортонормированный базис пространства , составленный из собственных векторов этого оператора.
Доказательство
(индукция по размерности пространства).n=1. Тогда любой ненулевой вектор v является и базисным, и собственным вектором, отвечающим некоторому собственному значению . Нормируем вектор v, получаем
ортонормированный базис из собственного вектора.
Допустим, утверждение верно для пространств размерности n-1.
Слайд 13
Перейдем к пространству Е размерности n.
Пусть b – собственный
вектор, отвечающий некоторому собственному значению.
Нормируем этот вектор, получаем единичный
собственный вектор . Дополним до базиса всего пространства, получим .Запускаем процесс ортогонализации, начиная с вектора , получим ортогональный базис .
Векторы образуют ортогональный базис n-1 – мерного подпространства М,
причем вектор .
Пространство М замкнуто относительно оператора и, по индукционному предположению, содержит ортонормированный базис из собственных векторов . Тогда есть искомый базис. QED
ератора (L замкнуто относительно оператора). векторВыберем в нем подпространство L размерности n-1, тогда в этом подпространстве существует ортонормированный базис из собственных векторов симметрического оператора (L замкнуто относительно оператора).
Перейдем к пространству Е размерности n. Выберем в нем подпространство L размерности n-1, тогда в этом подпространстве существует ортонормированныбазис из собственных векторов симметрического оп
Слайд 14
Следствие 2.6. Матрица симметрического линейного оператора с помощью соответственного выбора
ортонормированного базиса, может быть приведена к диагональному виду.
Следствие 2.7. Всякая
симметрическая матрица S подобна диагональной D , у которой на диагонали стоят собственные значения матрицы S игде P – ортогональная матрица.
Слайд 15 Пример. В некотором ортонормированном базисе в R3 линейное преобразование φ
задано матрицей Найти для φ ортонормированный базис из собственных
векторов и записать в нем матрицу преобразования. Шаг1. Нахождение СЗ
Слайд 16Шаг2. Нахождение СВ
Система
уравнений для собственных векторов:
В качестве первого вектора берем
Второй линейно
независимый собственный вектор ищем ортогональный к первому, т.е. как решение системыНапример