Системы двух линейных уравнений с двумя переменными 1 16.04.2020

переменными
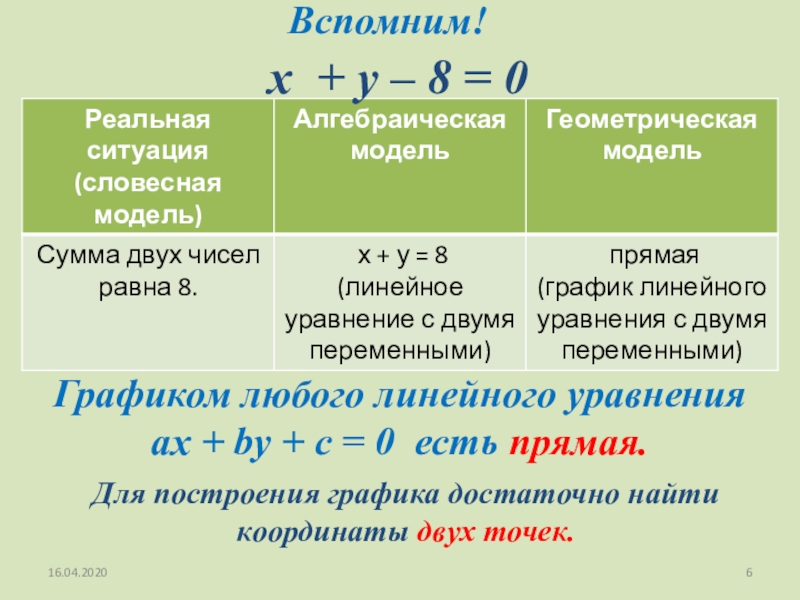
Решением уравнения с двумя неизвестными называется пара переменных, при подстановке

которых уравнение становится верным числовым равенством.

Уравнение вида:

называется линейным уравнением с
двумя переменными (где х, у - переменные,
а, b и с - некоторые числа).

(х;y)

переменной, при каждом из которых
уравнение обращается в верное
числовое

равенство.

Таких решений бесконечно много.

линейным уравнением
с одной переменной (где х – переменная,
k и

m некоторые числа).

у – 8 = 0
Вспомним!

= 0
3. Построим на координатной плоскости точки (х₁; у₁),

(х₂; у₂) и соединим прямой.

4. Прямая – есть график уравнения.

уравнений с двумя переменными.
(х;y)
Решение системы уравнений с двумя неизвестными называется

пара переменных, при подстановке которых уравнения становятся верными числовыми равенствами.

Решить систему - это значит найти все ее решения
или доказать, что их нет.

= 3х +1
у = 3х + 1

K1 ≠ K2, значит

прямые пересекаются.
Система имеет одно решение!

K1 = K2, значит прямые параллельны.
Система не имеет решения(она несовместимая)!

прямые совпадают.
Система имеет бесконечно много решений (она неопределённая)!

= 0 , у =

2х – 3.

-1

(1; -1)

2

(2; 1)

1

у = 2х - 3

-3

2. Построим график уравнения
х + 2у – 4 = 0 , 2у = -х + 4,
у = (-х + 4) : 2.

2

(0; 2)

у = (-х +4):2

3. Прямые пересекаются в
единственной точке А(2;1)

Ответ: (2; 1)

А

Графический способ
решения систем

виду линейной функции y = k x + m.
2.

Составляем расчётные таблицы для каждой функции.
3. Строим графики функций в одной координатной плоскости.
4. Определяем число решений:
Если прямые пересекаются, то одно решение пара чисел (х ; у) – координаты точки пересечения;
Если прямые параллельны, то нет решений;
Если прямые совпадают, то бесконечно много решений.
5. Записываем ответ.

= 0 , у =

(5 - х):2.

1

(1; 2)

3

(3; 1)

2

у = (5 – х):2

-2

2. Построим график уравнения
2 х + 4у + 3 = 0 , 4у = -2х - 3,
у = -(2х + 3) : 4.

-1,5

(-1,5; 0)

у = - (2х + 3):4

3. Прямые параллельны.

Ответ:
система не имеет решений

Графический способ
решения систем

(2,5; -2)

каком случае система имеет единственное решение?
Какая система является несовместимой?
О

какой системе говорят, что она неопределенна?
Что называется решением системы уравнений с двумя переменными?
Что значит решить систему уравнений?