Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления
Содержание
- 1. Системы счисления
- 2. Системы счисления§ 1. Кодирование чисел
- 3. Что такое система счисления?Система счисления — это
- 4. Непозиционные системы счисленияНепозиционная система счисления — это
- 5. Египетская десятичная система– 1– 10– 100– 1000– 10000– 100000– 1000000чертахомутверёвкалотоспалецлягушкачеловек= ?= 12352014 = ?
- 6. Римская система счисленияI – 1 (палец)
- 7. Римская система счисленияПравила:(обычно) не ставят больше трех
- 8. Римская система счисленияMCDLXVII =MMDCXLIV =MMMCCLXXII =CMXXVIII =
- 9. Римская система счисления3768 =2983 =1452 =1999 =
- 10. Римская система счислениятолько натуральные числа (дробные? отрицательные?)для записи больших чисел нужно вводить новые цифрысложно выполнять вычисления
- 11. Славянская система счисленияалфавитная система счисления (непозиционная)Часы Суздальского Кремля
- 12. ОпределенияПозиционная система: значение цифры определяется ее позицией
- 13. Другие позиционные системыдвоичнаявосьмеричнаяшестнадцатеричнаяи другие…101102= 124 + 023
- 14. Позиционные системы счисленияЗадача. В некоторой системе счисления
- 15. Системы счисления§ 2. Двоичная система счисления
- 16. Двоичная система счисленияОснование (количество цифр): 2Алфавит: 0,
- 17. Перевод в десятичную систему2 101001124 3
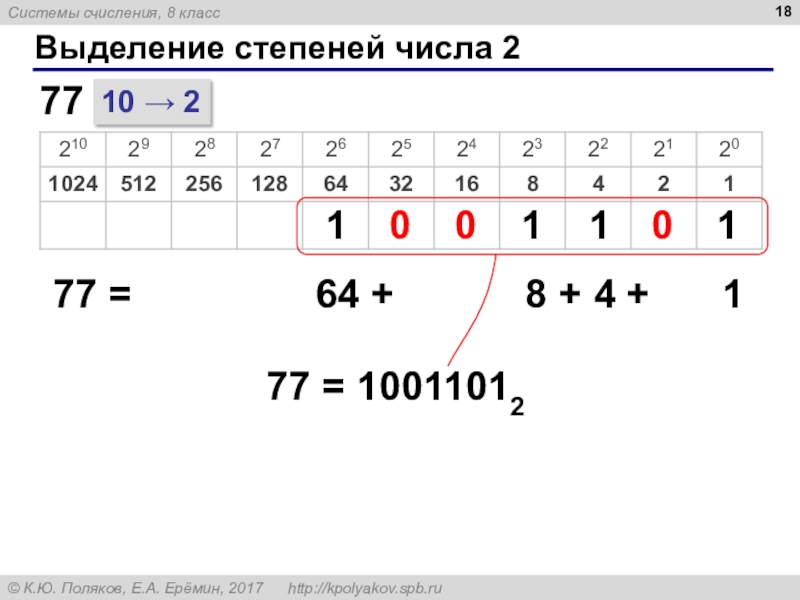
- 18. Выделение степеней числа 210 27777 =64
- 19. Другой способ100112= 1·24 + 0·23 + 0·22
- 20. Другой способ10 21919 = 100112
- 21. Сложение в двоичной системе1065311112 1
- 22. Сложение в двоичной системе
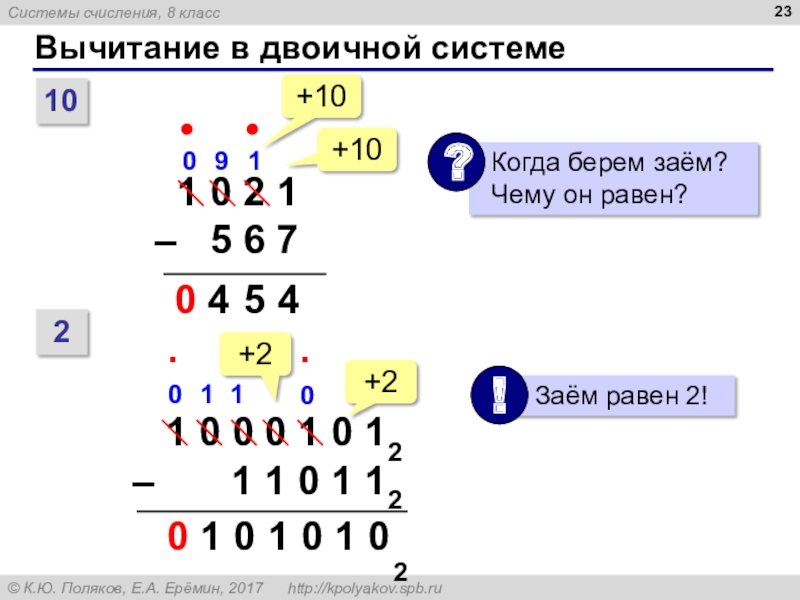
- 23. Вычитание в двоичной системе1045490210+10+10 1 0
- 24. Вычитание в двоичной системе
- 25. Системы счисления§ 3. Восьмеричная система счисления
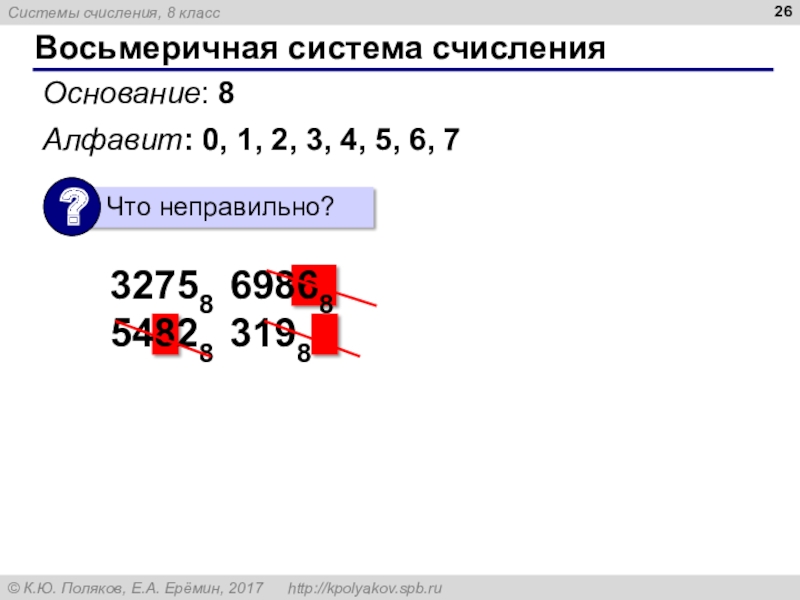
- 26. Восьмеричная система счисленияОснование: 8Алфавит: 0, 1, 2, 3, 4, 5, 6, 732758 69868 54828 3198
- 27. Из восьмеричной в десятичную8 10
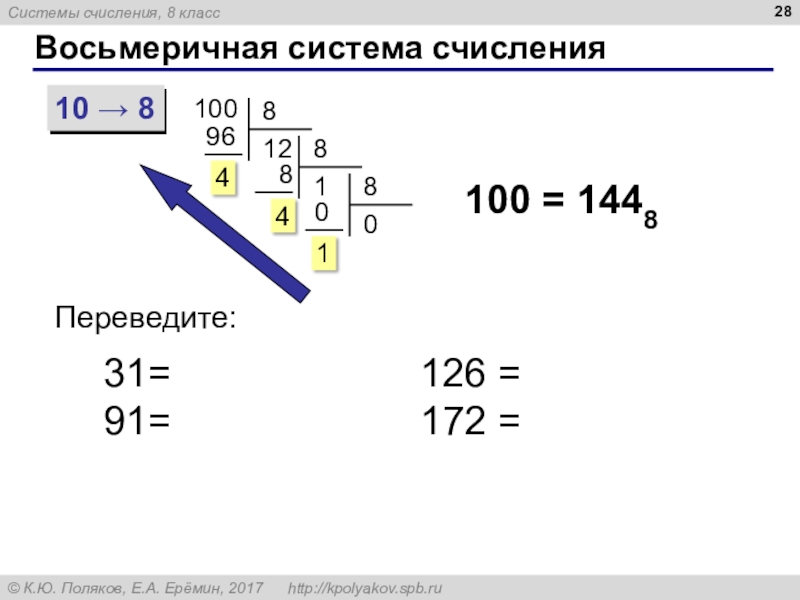
- 28. Восьмеричная система счисления10 8100100 = 1448Переведите:31= 91= 126 = 172 =
- 29. Связь с двоичной системой7538 = 7 82
- 30. Связь с двоичной системой8 = 23162516 =1
- 31. Перевод из двоичной в восьмеричную10010111011112Шаг 1. Разбить
- 32. Связь с двоичной системойПереведите в двоичную систему:3758 =52468 =Переведите в восьмеричную систему:10100112 =101011002 =
- 33. Сжатая запись двоичных кодов361368Запишите в сжатой форме:PDP-11, ДВК, СМ ЭВМ, БЭСМ, БК1
- 34. Сложениесложение1 5 68 + 6 6
- 35. Вычитаниевычитание4 5 68 – 2 7
- 36. Выполните сложение и вычитание
- 37. Системы счисления§ 4. Шестнадцатеричная система счисления
- 38. Шестнадцатеричная системаОснование: 16Алфавит: 0, 1, 2, 3,
- 39. Перевод в шестнадцатеричную систему1110 16444444 = 1BC16СBПереведите:31= 91= 126 = 172 =
- 40. Перевод из шестнадцатеричной системы16 10
- 41. Связь с двоичной системой счисления16 = 247F1A16
- 42. Перевод из двоичной системыШаг 1. Разбить на
- 43. Сжатая запись двоичных кодов5E5E16Запишите в сжатой форме:Intel, AMD, ARM
- 44. Сжатая запись двоичных кодовЗакодируйте рисунок и запишите в сжатой форме:
- 45. Связь с двоичной системой счисленияПереведите в двоичную
- 46. СложениесложениеA 5 B16+ C 7 E1611
- 47. ВычитаниевычитаниеС 5 B16– A 7 E16заём1
- 48. Арифметические действия1 В А16– A 5 916С В А16+ A 5 916
- 49. Конец фильмаПОЛЯКОВ Константин Юрьевичд.т.н., учитель информатикиГБОУ СОШ
- 50. Источники иллюстрацийitfoundations.commuseum.comp-school.ruиллюстрации художников издательства «Бином»авторские материалы
- 51. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Системы счисления
§ 1. Кодирование чисел
§ 2. Двоичная система счисления
§ 3.
Восьмеричная система счисления
Слайд 3Что такое система счисления?
Система счисления — это правила записи чисел
с помощью специальных знаков — цифр, а также соответствующие правила
выполнения операций с этими числами.Счёт на пальцах:
Унарная (лат. unus – один) – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)
только натуральные числа
запись больших чисел – длинная (1 000 000?)
Слайд 4Непозиционные системы счисления
Непозиционная система счисления — это такая система, в
которой значение цифры не зависит от её места (позиции) в
записи числа.унарная
египетская десятичная
римская
славянская
и другие…
Слайд 5Египетская десятичная система
– 1
– 10
– 100
– 1000
– 10000
– 100000
– 1000000
черта
хомут
верёвка
лотос
палец
лягушка
человек
=
?
= 1235
2014 = ?
Слайд 6Римская система счисления
I – 1 (палец)
V – 5
(раскрытая ладонь)
X – 10 (две ладони)
L – 50
C –
100 (Centum)D – 500 (Demimille)
M – 1000 (Mille)
Спасская башня Московского Кремля
Слайд 7Римская система счисления
Правила:
(обычно) не ставят больше трех
одинаковых цифр подряд
если
младшая цифра (только одна!) стоит слева от старшей, она вычитается
из суммы (частично непозиционная!)Примеры:
MDCXLIV =
1000
+ 500
+ 100
– 10
+ 50
– 1
+ 5
2389 = 2000 + 300 + 80 + 9
2389 = M M C C C L X X X I X
M M
CCC
LXXX
IX
= 1644
Слайд 10Римская система счисления
только натуральные числа (дробные? отрицательные?)
для записи больших чисел
нужно вводить новые цифры
сложно выполнять вычисления
Слайд 11Славянская система счисления
алфавитная система счисления (непозиционная)
Часы Суздальского Кремля
Слайд 12Определения
Позиционная система: значение цифры определяется ее позицией в записи числа.
Алфавит
системы счисления — это используемый в ней набор цифр.
Основание системы
счисления — это количество цифр в алфавите (мощность алфавита).Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
6 3 7 5
5
70
300
6000
3 2 1 0
разряды
= 6·103 + 3·102 + 7·101 + 5·100
развёрнутая форма записи числа
Слайд 13Другие позиционные системы
двоичная
восьмеричная
шестнадцатеричная
и другие…
101102
= 124 + 023 + 122 +
121 + 020
4 3 2 1 0
= 22
1458
2 1
0= 182 + 481 + 580
= 101
12316
2 1 0
= 1162 + 2161 + 3160
= 291
1235
2 1 0
= 152 + 251 + 350
= 38
4567
1022
36512
5788
1729
5214
Слайд 14Позиционные системы счисления
Задача. В некоторой системе счисления число 58 записывается
как 46x. Определите основание x этой системы счисления.
46x
1 0
= 4x1
+ 6x04x + 6 = 58
4x = 52
x = 13
= 4x + 6
Переведём 46x в десятичную систему:
Слайд 16Двоичная система счисления
Основание (количество цифр): 2
Алфавит: 0, 1
длинная запись чисел:
1024 = 100000000002
запись однородна (только 0 и 1)
нужны только
устройства с двумя состояниямикомпьютеру проще выполнять вычисления (умножение сводится сложению и т.п.)
Слайд 17Перевод в десятичную систему
2 10
100112
4 3 2 1 0
разряды
=
1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16
+ 2 + 1 = 1910 2
Выделение степеней числа 2:
21 = 16 + 5
21 = 124 + 023 + 122 + 021 + 120
= 16 + 4 + 1
24
24
22
20
= 101012
Слайд 19Другой способ
100112
= 1·24 + 0·23 + 0·22 + 1·21 +
1·20
= (1·23 + 0·22 + 0·21 + 1·20)·2 + 1
10012
= 100112 : 2деление нацело
4 3 2 1 0
Слайд 21Сложение в двоичной системе
10
6
5
3
1
1
1
1
2
1 0 1 1
02
+ 1 1 1 0 1 12
1
1
0
0
1
0
1
1
0
2
1
1
1
1 + 1 =
2 = 1021 + 1 + 1 = 3 = 112
Слайд 26Восьмеричная система счисления
Основание: 8
Алфавит: 0, 1, 2, 3, 4, 5,
6, 7
32758 69868
54828 3198
Слайд 27Из восьмеричной в десятичную
8 10
1448
2 1 0
разряды
=
1·82 + 4·81 + 4·80
= 64 + 32 + 4
= 100Переведите:
128 =
578 =
648 =
778 =
1208
57008
Слайд 29Связь с двоичной системой
7538 = 7 82 + 581 +
380
= 7 26 + 523 + 320
7538 = (1 22
+ 1 21 + 1 20) 26 + (1 22 + 0 21 + 1 20) 23 +
(0 22 + 1 21 + 1 20) 20
7538 = 1 28 + 1 27 + 1 26 +
1 25 + 0 24 + 1 23 +
0 22 + 1 21 + 1 20
= 1111010112
8 = 23
Слайд 31Перевод из двоичной в восьмеричную
10010111011112
Шаг 1. Разбить на триады, начиная
справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной
восьмеричной цифрой:1
3
5
7
Ответ: 10010111011112 = 113578
001 001 011 101 1112
1
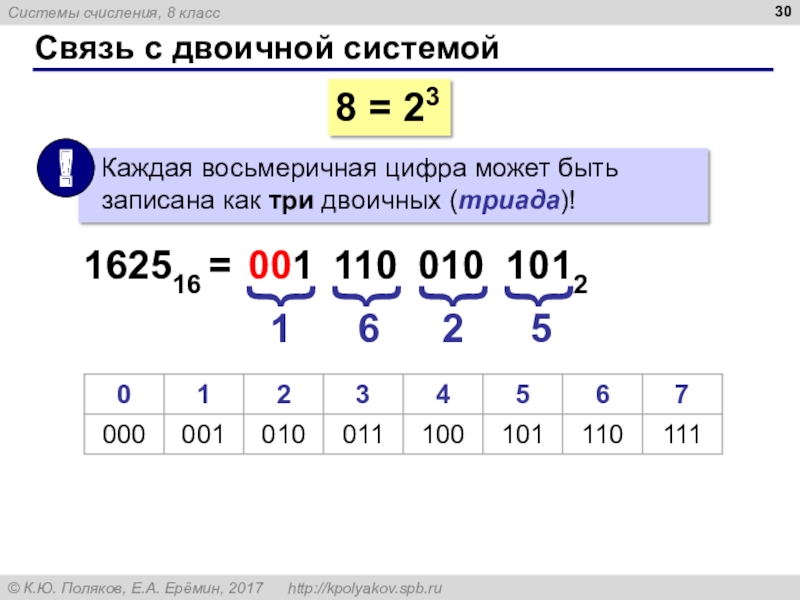
Слайд 32Связь с двоичной системой
Переведите в двоичную систему:
3758 =
52468 =
Переведите в
восьмеричную систему:
10100112 =
101011002 =
Слайд 34Сложение
сложение
1 5 68
+ 6 6 28
1
1
6 +
2 = 8 = 8 + 0
5 + 6 +
1 = 12 = 8 + 41 + 6 + 1 = 8 = 8 + 0
1
1 в перенос
1 в перенос
1
08
0
4
1 в перенос
Слайд 35Вычитание
вычитание
4 5 68
– 2 7 78
(6 +
8) – 7 = 7
(5 – 1 + 8)
– 7 = 5(4 – 1) – 2 = 1
заём
78
1
5
заём
Слайд 38Шестнадцатеричная система
Основание: 16
Алфавит: 0, 1, 2, 3, 4, 5, 6,
7, 8, 9,
A,
10
B,
11
C,
12
D,
13
E,
14
F
15
34AF516
5BG616 9FF6116 ADH2316
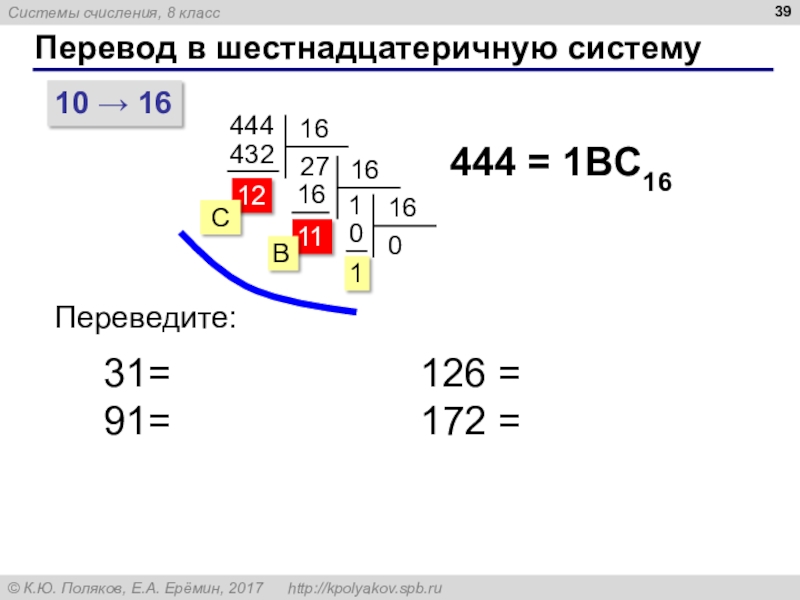
Слайд 40Перевод из шестнадцатеричной системы
16 10
1BC16
2 1 0
разряды
=
1·162 + 11·161 + 12·160
= 256 + 176 + 12
= 444B
C
Переведите:
1216 =
5A16 =
B916 =
AB16 =
12016
570016
Слайд 42Перевод из двоичной системы
Шаг 1. Разбить на тетрады, начиная справа:
0001
0010 1110 11112
Шаг 2. Каждую тетраду записать одной
шестнадцатеричной цифрой:0001 0010 1110 11112
1
2
E
F
Ответ: 10010111011112 = 12EF16
10010111011112
Слайд 45Связь с двоичной системой счисления
Переведите в двоичную систему:
EA123816 =
Переведите
в шестнадцатеричную систему :
111110100112 =
Переведите в восьмеричную систему :
2FA16
= Переведите в шестнадцатеричную систему :
1658 =
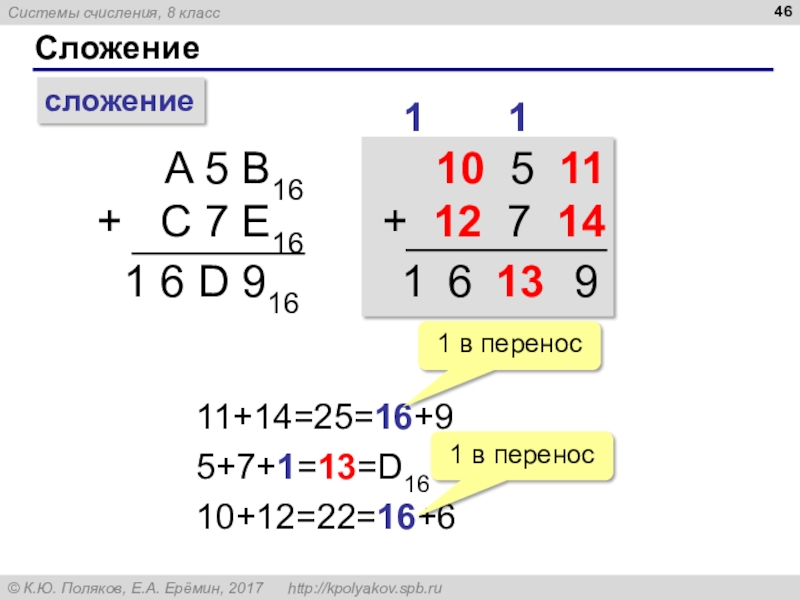
Слайд 46Сложение
сложение
A 5 B16
+ C 7 E16
1
1 6 D 916
10
5 11
+ 12 7 14
11+14=25=16+9
5+7+1=13=D16
10+12=22=16+6
1
1 в перенос
1 в перенос
13
9
6
1
Слайд 47Вычитание
вычитание
С 5 B16
– A 7 E16
заём
1 D D16
12 5
11
– 10 7 14
(11+16)–14=13=D16
(5 – 1)+16 – 7=13=D16
(12 – 1)
– 10 = 1заём
13
1
13
Слайд 49Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г.
Санкт-Петербург
kpolyakov@mail.ru
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО
ПГГПУ, г. Пермьeremin@pspu.ac.ru