Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления
Содержание
- 1. Системы счисления
- 2. Система счисления- это совокупность правил и приемов записи чисел с помощью набора цифровых знаковУнарнаяПозиционнаяНепозиционная
- 3. Основные понятия систем счисленияКоличество цифр, необходимых для
- 4. Системы счисления
- 5. Позиционная система счисленияЧисло в системе счисления с
- 6. Правило 1 Перевод числа x из системы
- 7. Правило 2 Перевод числа x из системы
- 8. Пример: Перевести число 75 из десятичной системы
- 9. Слайд 9
- 10. Перевод чисел из восьмеричной системы счисления в
- 11. Пример (перевод дробной части)0,37510→ O,Y2
- 12. Формы представления чиселС фиксированной точкой(естественная форма)С плавающей точкой (нормализованный вид)
- 13. Естественная форма P-S ≤ N ≤ Рm
- 14. С плавающей точкой Х10 =±М10*10±К , где
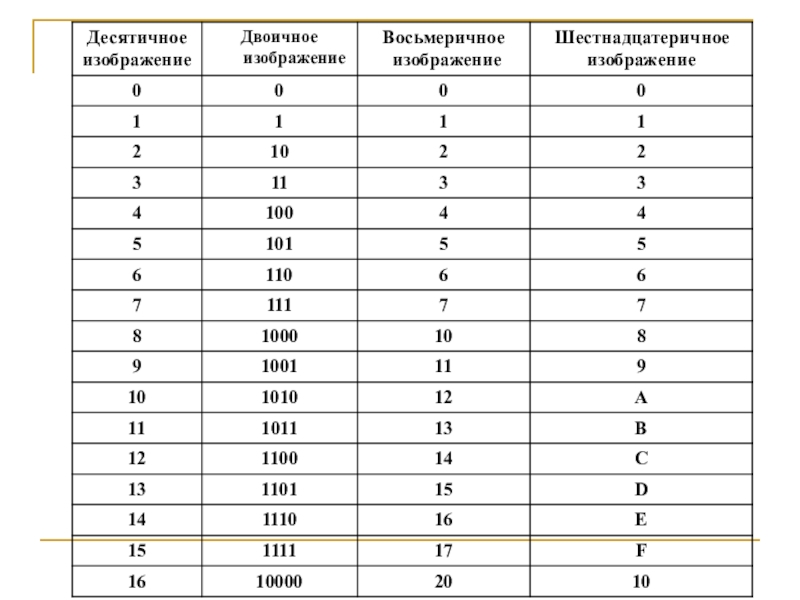
- 15. Сводная таблица переводов целых чисел
- 16. Сводная таблица переводов целых чисел
- 17. Скачать презентанцию
Система счисления- это совокупность правил и приемов записи чисел с помощью набора цифровых знаковУнарнаяПозиционнаяНепозиционная
Слайды и текст этой презентации
Слайд 2Система счисления
- это совокупность правил и приемов записи чисел с
помощью набора цифровых знаков
Слайд 3Основные понятия систем счисления
Количество цифр, необходимых для записи числа в
системе, называют основанием системы счисления.
Основание системы записывается справа от числа
в нижнем индексе:, , и т.д.
Слайд 5Позиционная система счисления
Число в системе счисления с основанием P равно:
AnAn-1An-2 … A1A0,A-1…A-s = Аn*Pn + An-1*Pn-1 + ... +
A1*P1 + А0*P0 + A-1*P-1 + А-2*P-2 + ... А-s*P-sнижние индексы - определяют месторасположение цифры в числе
n и s - количества разрядов для записи целой и дробной части числа соответственно.
Слайд 6Правило 1
Перевод числа x из системы счисления основанием P
в систему счисления с основанием Q осуществляется путем представления числа
х по степеням основания P. Все вычисления выполняются в системе счисления с основанием Q, т. е. основание P и цифры исходного числа должны также быть выражены в системе счисления с основанием Q.На практике такой порядок перевода чисел используется при переводе в десятичную систему счисления.
23Е16 = ?10 = 2*162+3*161+ 14*160 = 57410
10788 = 1*83+0*82+7*81+6*80 = 57410
Слайд 7Правило 2
Перевод числа x из системы счисления с основанием
P в систему счисления с основанием Q заключается в последовательном
нахождении остатков от деления числа x на основание Q, при этом процесс продолжается до тех пор, пока частное от деления не будет меньше основания Q.Все вычисления выполняются в системе счисления с основанием P, т.е. основание Q должно также быть выражено в системе счисления с основанием P.
Остатки от деления должны быть выражены цифрами системы счисления с основанием Q. Представление искомого числа в системе счисления с основанием Q получается выписыванием последнего частного и остатков от деления в обратном порядке.
Слайд 8Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную
и шестнадцатеричную
Ответ: 7510 = 1 001 0112 = 1138
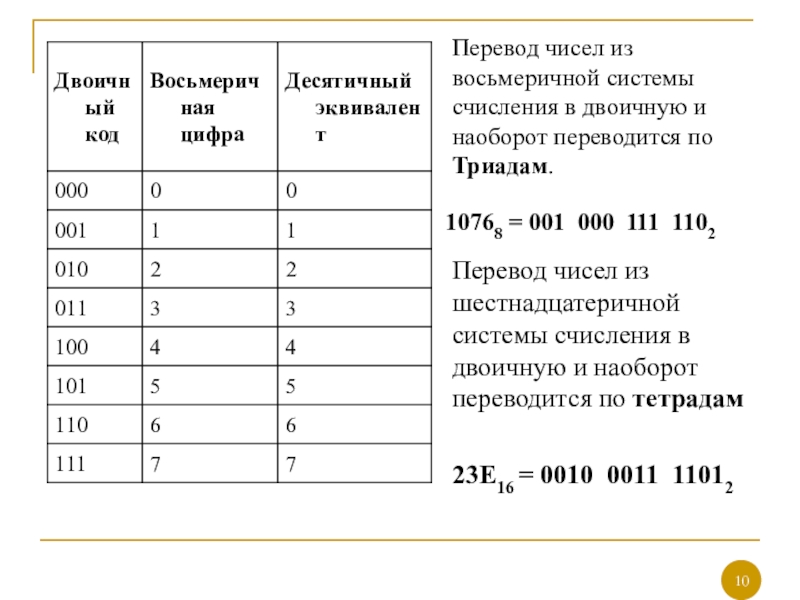
= 4B16. 
Слайд 10Перевод чисел из восьмеричной системы счисления в двоичную и наоборот
переводится по Триадам.
10768 = 001 000 111 1102
Перевод чисел из
шестнадцатеричной системы счисления в двоичную и наоборот переводится по тетрадам23E16 = 0010 0011 11012
Слайд 11Пример (перевод дробной части)
0,37510→ O,Y2
0, 375*2 =
0, 7500, 75*2 = 1, 50
0, 5*2 = 1 , 0
0,37510 = 0,0112
Слайд 12Формы представления чисел
С фиксированной точкой
(естественная форма)
С плавающей точкой
(нормализованный вид)
Слайд 13Естественная форма
P-S ≤ N ≤ Рm - P-S
При р=2,
m=10 и S=6 0,015 ≤ N ≤
1024.Если в результате операции получится число, выходящее за допустимый диапазон, происходит переполнение разрядной сетки и дальнейшее вычисления теряют смысл.
С фиксированной точкой все числа изображаются в виде
последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.
0,25; -10,44; +0,9781
Пример: Диапазон чисел (N) в системе счисления с основанием Р при наличии m разрядов в целой части и S разрядов в дробной (без учета знака числа) будет:
Слайд 14С плавающей точкой
Х10 =±М10*10±К ,
где М10 – мантисса,
0,1≤ М10< 1, К-порядок, целое положительно десятичное число.
Пример: -123410= -0,1234*104,
0,003=0,3*10-2При нормализации выполняется деление числа на 4 составляющих: знак числа, мантисса, знак порядка, порядок.
Для произвольной системы счисления.
Хр =± Мр*P±К , Р-1 ≤ М< 1
Определение: Число Х10 называется нормализованным, если оно представлено в виде
