Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СИСТЕМЫ СЧИСЛЕНИЯ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Содержание
- 1. СИСТЕМЫ СЧИСЛЕНИЯ МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
- 2. Ключевые словасистема счисленияцифраалфавитпозиционная система счисленияоснованиеразвёрнутая форма записи числасвёрнутая форма записи числа
- 3. Система счисления - это знаковая система, в
- 4. Узловые числа обозначаются цифрами.Узловые и алгоритмические числаАлгоритмические
- 5. Простейшая и самая древняя система - унарная
- 6. Римская система счисления40=XL1935MCMXXX28XXVIIIVНепозиционная система счисленияСистема счисления называется
- 7. Система счисления называется позиционной, если количественный эквивалент
- 8. Цифры 1234567890 сложились в Индии около 400
- 9. Развёрнутая формаНапример, в числе 536 первая пятерка
- 10. Развёрнутая формаВсякое десятичное число можно представить как
- 11. В позиционной системе счисления с основанием q
- 12. Aq = ± (an–1 qn–1+ an–2
- 13. ЗаданияЗаписать числа в развернутой форме:2853864893,73534,07 012012012-3-2-1013-1-2= 2∙102+8∙101+5∙100= 3∙103+8∙102+6∙101+4∙100= 8∙102+9∙101+3∙100+7∙10-1+3∙10-2+5∙10-3= 3∙101+4∙100+0∙10-1+7∙10-2
- 14. Для записи чисел в позиционной системе
- 15. Перевод в десятичную систему счисленияНапример, число
- 16. Двоичная система счисленияДвоичной системой счисления называется позиционная
- 17. an–1an–2…a1a0 = an–18n–1+an–28n–2+…+a080Пример: 10638 =183 +082+681+380=56310.Для перевода
- 18. Основание: q = 16.Алфавит: 0, 1, 2,
- 19. Задание Перевести числа в десятичную систему счисления.1101012,
- 20. Опорный конспектНепозиционнаяВ позиционной системе счисления с основанием
- 21. Система счисления - это знаковая система, в
- 22. Домашнее задание§ 1.1.1, № 17, 18, 23 (из рабочей тетради)
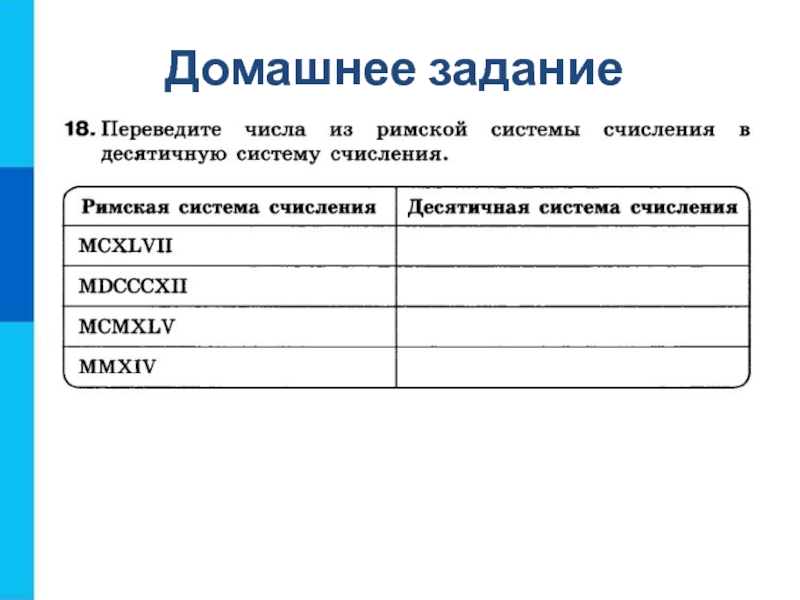
- 23. Домашнее задание
- 24. Домашнее задание
- 25. Домашнее задание
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Ключевые слова
система счисления
цифра
алфавит
позиционная система счисления
основание
развёрнутая форма записи числа
свёрнутая форма записи
числа
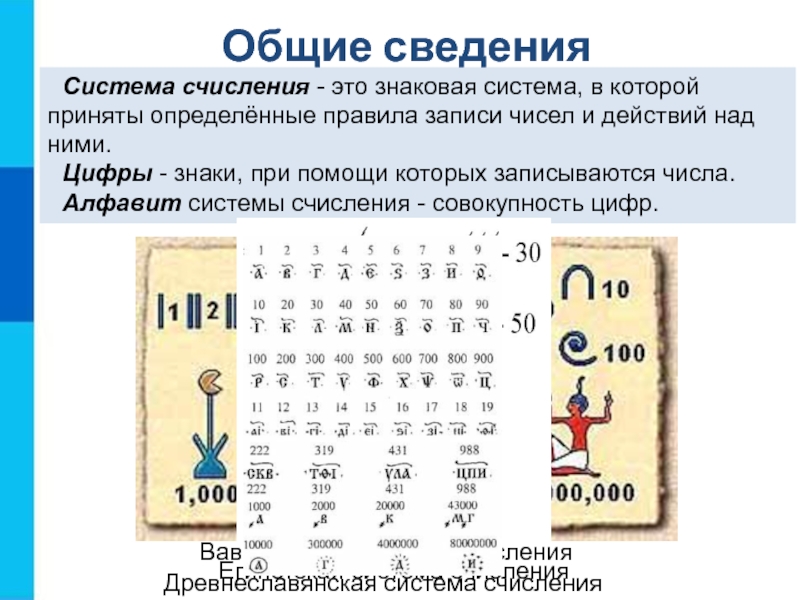
Слайд 3Система счисления - это знаковая система, в которой приняты определённые
правила записи чисел и действий над ними.
Цифры - знаки,
при помощи которых записываются числа.Алфавит системы счисления - совокупность цифр.
Общие сведения
Древнеславянская система счисления
Вавилонская система счисления
Египетская система счисления
Слайд 4Узловые числа обозначаются цифрами.
Узловые и алгоритмические числа
Алгоритмические числа получаются в
результате каких-либо операций из узловых чисел.
100 +
10
+ =
Слайд 5Простейшая и самая древняя система - унарная система счисления. В
ней для записи любых чисел используется всего один символ -
палочка, узелок, зарубка, камушек.Унарная система счисления
Узелковое письмо «кипу»
Зарубки
Примеры узлов «кипу»
Узелки, дощечки
Камушки
Слайд 6Римская система счисления
40
=
X
L
1935
M
C
M
X
X
X
28
X
X
V
I
I
I
V
Непозиционная система счисления
Система счисления называется непозиционной, если количественный
эквивалент (количественное значение) цифры в числе не зависит от её
положения в записи числа.Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:
каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Слайд 7Система счисления называется позиционной, если количественный эквивалент цифры в числе
зависит от её положения в записи числа.
Основание позиционной системы счисления
равно количеству цифр, составляющих её алфавит.Алфавит десятичной системы составляют цифры
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Позиционная система счисления
Слайд 8Цифры 1234567890 сложились в Индии около 400 г. н. э.
Арабы
стали пользоваться подобной нумерацией около 800 г. н. э.
Примерно в
1200 г. н. э. эту нумерацию начали применять в Европе.Десятичная система счисления
Слайд 9Развёрнутая форма
Например, в числе 536 первая пятерка обозначает пять сотен,
вторая – пять десятков, третья – пять единиц. Одна и
та же цифра в зависимости от позиции в записи числа обозначает разные величины.Слайд 10Развёрнутая форма
Всякое десятичное число можно представить как сумму произведений составляющих
его цифр на соответствующие степени десятки. То же самое относится
и к десятичным дробям.100 = 1
101 = 10 10-1 = 0,1
102 = 100 10-2 = 0,01
103 = 1000 10-3 = 0,001 и т.д.
Например,
26,387 = 2 ∙ 101 + 6 ∙ 100 + 3 ∙ 10-1 + 8 ∙ 10-2 + 7 ∙ 10-3.
Слайд 11В позиционной системе счисления с основанием q любое число может
быть представлено в виде:
Aq = ± (an–1qn–1+ an–2 qn–2+…+
a0 q0+ a–1q–1+…+ a–m q–m) Здесь:
А - число;
q - основание системы счисления;
ai - цифры, принадлежащие алфавиту данной системы счисления;
n - количество целых разрядов числа;
m - количество дробных разрядов числа;
qi - «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.
Основная формула
Слайд 12Aq = ± (an–1 qn–1+ an–2 qn–2+…+ a0
q0+ a–1 q–1+…+ a–m q–m)
Примеры записи
чисел в развёрнутой форме:2012=2103 +0102 +1101 +2100
0,125=110-1 +210-2 +510–3
14351,1=1104 +4103 +3102 +5101 +1100 +110–1
Развёрнутая форма
Слайд 13Задания
Записать числа в развернутой форме:
285
3864
893,735
34,07
0
1
2
0
1
2
0
1
2
-3
-2
-1
0
1
3
-1
-2
= 2∙102+8∙101+5∙100
= 3∙103+8∙102+6∙101+4∙100
= 8∙102+9∙101+3∙100+7∙10-1+3∙10-2+5∙10-3
= 3∙101+4∙100+0∙10-1+7∙10-2
Слайд 14Для записи чисел в позиционной системе с основанием n используется
n цифр.
1011012 36718 3B8F16
Слайд 15Перевод
в десятичную систему счисления
Например, число 2113 содержит в себе
1 единицу, 1 тройку и 2 девятки.
2113 = 2∙32
+ 1∙31 + 1∙30 = 18 + 3 + 1 = 2210Аналогично переводятся и дробные числа.
101,112 = 1∙22 + 0∙21 + 1∙20 + 1∙2-1 + 1∙2-2 = = 4 + 0 + 1 + 0,5 + 0,25 = 5,7510.
Перевод осуществляется разложением по степеням основания
Слайд 16Двоичная система счисления
Двоичной системой счисления называется позиционная система счисления с
основанием 2.
Двоичный алфавит: 0 и 1.
Для целых двоичных чисел можно
записать:an–1an–2…a1a0 = an–12n–1 + an–22n–2 +…+ a020
Например:
100112 =124+023+022+121+120 = 24 +21 + 20 =1910
Правило перевода двоичных чисел
в десятичную систему счисления:
Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа
Слайд 17an–1an–2…a1a0 = an–18n–1+an–28n–2+…+a080
Пример: 10638 =183 +082+681+380=56310.
Для перевода целого восьмеричного числа
в десятичную систему счисления следует перейти к его развёрнутой записи
и вычислить значение получившегося выражения.Восьмеричная система счисления
Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
Слайд 18Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5,
6, 7, 8, 9, A, B, C, D, E, F.
Шестнадцатеричная
система счисления3АF16 =3162+10161+15160 =768+160+15=94310.
Слайд 19Задание
Перевести числа в десятичную систему счисления.
1101012, 34,25, 2А3,816.
1101012 =
1∙25 + 1∙24 + 0∙23 + 1∙22 + 0∙21 +
1∙20 = = 32 + 16 + 0 + 4 + 0 + 1 = 531034,25 = 3∙51 + 4∙50 + 2∙5-1 = 15 + 4 + 0,4 =19,410
2А3,816 = 2∙162 + 10∙161 + 3∙160 + 8∙16-1 = = 512 + 160 + 3 + 0,5 = 675,510
0
1
2
3
4
5
-1
0
1
-1
0
1
2
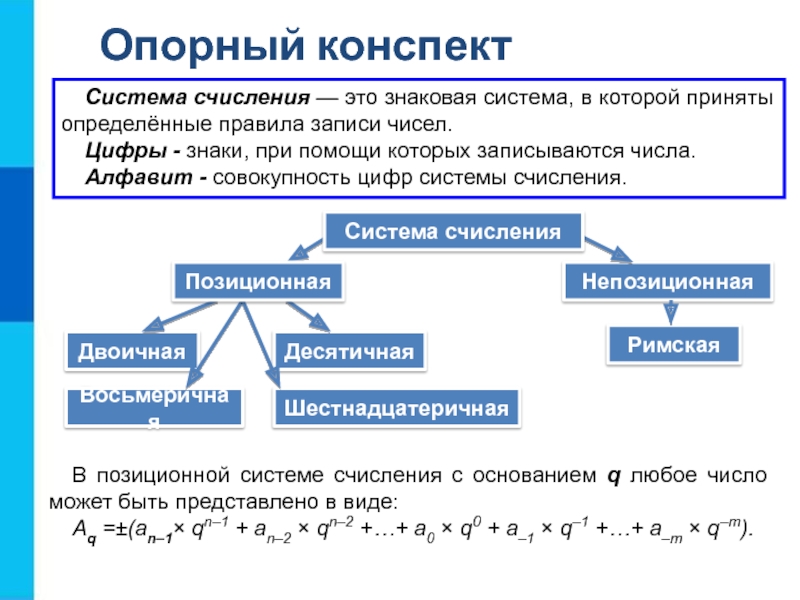
Слайд 20Опорный конспект
Непозиционная
В позиционной системе счисления с основанием q любое число
может быть представлено в виде:
Aq =±(an–1 qn–1 + an–2
qn–2 +…+ a0 q0 + a–1 q–1 +…+ a–m q–m).Система счисления — это знаковая система, в которой приняты определённые правила записи чисел.
Цифры - знаки, при помощи которых записываются числа.
Алфавит - совокупность цифр системы счисления.
Система счисления
Двоичная
Десятичная
Восьмеричная
Шестнадцатеричная
Римская
Позиционная
Слайд 21Система счисления - это знаковая система, в которой приняты определённые
правила записи чисел.
Система счисления называется позиционной, если количественный эквивалент
цифры в числе зависит от её положения в записи числа. В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Aq = ± (an–1qn–1 + an–2qn–2 +…+ a0q0 + a–1q–1 +…+ a–mq–m)
Здесь:
А - число;
q - основание системы счисления;
ai - цифры, принадлежащие алфавиту данной системы счисления;
n - количество целых разрядов числа;
m - количество дробных разрядов числа;
qi - «вес» i-го разряда.
Самое главное