Слайд 1Системы управления химико-технологическим Процессами
Погляд Сергей Степанович
Кафедра «Радиохимия»
ДИТИ НИЯУ МИФИ
Слайд 2Тест - опрос
На каждый вопрос дается 30 секунд
Слайд 3Вопрос №1
С точки зрения линейной теории автоматического регулирования
Важно учитывать
конструкцию аппаратов и химическую природу процессов
Важно учитывать конструкцию аппаратов, химическая
природа процессов безразлична процессов
Важно учитывать химическую природу процессов, конструкция аппаратов безразлична
Безразлично из каких элементов составлена САР, важно лишь математическое описание этих элементов
Безразлично из каких элементов составлена САР и их математическое описание – важен лишь коэффициент ослабления внешних воздействий
Системы управления химико-технологическим процессами
Слайд 4Вопрос №2
Статикой называется
Установившийся режим звена или системы, при котором
передаточная функция входного и выходного сигнала звена (или системы) постоянны
во времени
Установившийся режим звена или системы, при котором входной и выходной сигналы звена (или системы) постоянны во времени
Режим звена или системы, при котором передаточная функция входного и выходного сигнала звена (или системы) при снятии внешнего воздействия возвращается к стационарному значению
Режим звена или системы, при котором входной и выходной сигналы звена (или системы) при снятии внешнего воздействия возвращается к стационарному значению
Режим звена или системы, при котором передаточная функция входного и выходного сигнала звена (или системы) без снятии внешнего воздействия возвращается к стационарному значению
Режим звена или системы, при котором входной и выходной сигналы звена (или системы) без снятии внешнего воздействия возвращается к стационарному значению
Системы управления химико-технологическим процессами
Слайд 5Вопрос №3
Для перехода от нелинейных звеньев к линейному представлению
применяют
Линеаризацию касательной
Метод наименьших квадратов
Ступенчатое приближение
Метод секущих
Метод кусочно-линейной линеаризации
Линейную фильтрацию по
нескоьким точкам
Системы управления химико-технологическим процессами
Слайд 6Вопрос №4
В динамике
Передаточная функция звена (системы) изменяется во времени
вследствие изменения входной величины
Передаточная функция звена (системы) изменяется в зависимости
от времени
Выходная величина звена (системы) изменяется во времени вне зависимости от входной величины
Выходная величина звена (системы) изменяется во времени вследствие изменения входной величины
Выходная величина звена (системы) изменяется во времени как в зависимости от входной величины так и в зависимости от времени
Системы управления химико-технологическим процессами
Слайд 7Вопрос №5
Суть преобразования Лапласса
заключается в том, что функции комплексного переменного
x(p) ставится в соответствие функция действительного переменного х(t)
заключается в том,
что функции действительного переменного х(t) ставится в соответствие функция комплексного переменного x(p)
заключается в том, что в функцию действительного переменного х(t) подставляется новая переменная p
заключается в том, что в функцию комплексного переменного х(p) подставляется новая переменная t
является математической абстракцией
Системы управления химико-технологическим процессами
Слайд 8Вопрос №6
Операции нахождения оригинала выходной величины по изображению
Интегрирование по частям
Преобразование
Лапласа
Обратное преобразование лапласса
Решение характеристического уравнения
Решение дифференциального уравнения высоких порядков
Решение нелинейного
дифференциального уравнения
Системы управления химико-технологическим процессами
Слайд 9Вопрос №7
Реакция звена на единичную ступенчатую функцию называется
Передаточной функцией
Переходной
характеристикой
Изображением функциии
Импульсной переходной характеристикой
Весовой функцией
Частотной характеристикой
Системы управления химико-технологическим процессами
Слайд 10Вопрос №7
Реакция звена на единичный импульс
Передаточной функцией
Переходной характеристикой
Изображением функциии
Импульсной
переходной характеристикой
Весовой функцией
Частотной характеристикой
Системы управления химико-технологическим процессами
Слайд 11Вопрос №8
Реакция звена на гармонические колебания на входе называется
Передаточной функцией
Переходной
характеристикой
Изображением функциии
Импульсной переходной характеристикой
Весовой функцией
Частотной характеристикой
Системы управления химико-технологическим процессами
Слайд 12Вопрос №9
Передаточная функция замкнутой цепи равна передаточной функции прямой цепи,
деленной на единицу плюс (о.о.с.) или минус (п.о.с.) передаточная функция
цепи обратной связи, умноженная на передаточную функцию прямой цепи.
Передаточная функция замкнутой цепи равна передаточная функция цепи обратной связи, умноженная на передаточную функцию прямой цепи.
Передаточная функция замкнутой цепи равна сумме передаточной функция цепи обратной связи и прямой цепи
Передаточная функция замкнутой цепи равна максимуму из передаточной функции цепи обратной связи и передаточную функции прямой цепи
Передаточная функция замкнутой цепи равна минимуму из передаточной функции цепи обратной связи и передаточную функции прямой цепи
Передаточная функция замкнутой цепи равна среднему гармоническому из передаточной функции цепи обратной связи и передаточную функции прямой цепи
Системы управления химико-технологическим процессами
Слайд 13Вопрос №10
Изображение выходного сигнала
Изображение входного сигнала
Дифференциальное уравнение, описывающее систему
Комплексная передаточная
функция
Передаточная функция
Уравнение Эйлера
Системы управления химико-технологическим процессами
Слайд 15Вопрос №1
С точки зрения линейной теории автоматического регулирования
Важно учитывать
конструкцию аппаратов и химическую природу процессов
Важно учитывать конструкцию аппаратов, химическая
природа процессов безразлична процессов
Важно учитывать химическую природу процессов, конструкция аппаратов безразлична
Безразлично из каких элементов составлена САР, важно лишь математическое описание этих элементов
Безразлично из каких элементов составлена САР и их математическое описание – важен лишь коэффициент ослабления внешних воздействий
Системы управления химико-технологическим процессами
Слайд 16Вопрос №2
Статикой называется
Установившийся режим звена или системы, при котором
передаточная функция входного и выходного сигнала звена (или системы) постоянны
во времени
Установившийся режим звена или системы, при котором входной и выходной сигналы звена (или системы) постоянны во времени
Режим звена или системы, при котором передаточная функция входного и выходного сигнала звена (или системы) при снятии внешнего воздействия возвращается к стационарному значению
Режим звена или системы, при котором входной и выходной сигналы звена (или системы) при снятии внешнего воздействия возвращается к стационарному значению
Режим звена или системы, при котором передаточная функция входного и выходного сигнала звена (или системы) без снятии внешнего воздействия возвращается к стационарному значению
Режим звена или системы, при котором входной и выходной сигналы звена (или системы) без снятии внешнего воздействия возвращается к стационарному значению
Системы управления химико-технологическим процессами
Слайд 17Вопрос №3
Для перехода от нелинейных звеньев к линейному представлению
применяют
Линеаризацию касательной
Метод наименьших квадратов
Ступенчатое приближение
Метод секущих
Метод кусочно-линейной линеаризации
Линейную фильтрацию по
нескоьким точкам
Системы управления химико-технологическим процессами
Слайд 18Вопрос №4
В динамике
Передаточная функция звена (системы) изменяется во времени
вследствие изменения входной величины
Передаточная функция звена (системы) изменяется в зависимости
от времени
Выходная величина звена (системы) изменяется во времени вне зависимости от входной величины
Выходная величина звена (системы) изменяется во времени вследствие изменения входной величины
Выходная величина звена (системы) изменяется во времени как в зависимости от входной величины так и в зависимости от времени
Системы управления химико-технологическим процессами
Слайд 19Вопрос №5
Суть преобразования Лапласса
Заключается в том, что функции комплексного переменного
x(p) ставится в соответствие функция действительного переменного х(t)
Заключается в том,
что функции действительного переменного х(t) ставится в соответствие функция комплексного переменного x(p)
Заключается в том, что в функцию действительного переменного х(t) подставляется новая переменная p
Заключается в том, что в функцию комплексного переменного х(p) подставляется новая переменная t
Является математической абстракцией
Системы управления химико-технологическим процессами
Слайд 20Вопрос №6
Операции нахождения оригинала выходной величины по изображению
Интегрирование по частям
Преобразование
Лапласа
Обратное преобразование Лапласса
Решение характеристического уравнения
Решение дифференциального уравнения высоких порядков
Решение нелинейного
дифференциального уравнения
Системы управления химико-технологическим процессами
Слайд 21Вопрос №7
Реакция звена на единичную ступенчатую функцию называется
Передаточной функцией
Переходной
характеристикой
Изображением функциии
Импульсной переходной характеристикой
Весовой функцией
Частотной характеристикой
Системы управления химико-технологическим процессами
Слайд 22Вопрос №7
Реакция звена на единичный импульс
Передаточной функцией
Переходной характеристикой
Изображением функциии
Импульсной
переходной характеристикой
Весовой функцией
Частотной характеристикой
Системы управления химико-технологическим процессами
Слайд 23Вопрос №8
Реакция звена на гармонические колебания на входе называется
Передаточной функцией
Переходной
характеристикой
Изображением функциии
Импульсной переходной характеристикой
Весовой функцией
Частотной характеристикой
Системы управления химико-технологическим процессами
Слайд 24Вопрос №9
Передаточная функция замкнутой цепи равна передаточной функции прямой цепи,
деленной на единицу плюс (о.о.с.) или минус (п.о.с.) передаточная функция
цепи обратной связи, умноженная на передаточную функцию прямой цепи.
Передаточная функция замкнутой цепи равна передаточная функция цепи обратной связи, умноженная на передаточную функцию прямой цепи.
Передаточная функция замкнутой цепи равна сумме передаточной функция цепи обратной связи и прямой цепи
Передаточная функция замкнутой цепи равна максимуму из передаточной функции цепи обратной связи и передаточную функции прямой цепи
Передаточная функция замкнутой цепи равна минимуму из передаточной функции цепи обратной связи и передаточную функции прямой цепи
Передаточная функция замкнутой цепи равна среднему гармоническому из передаточной функции цепи обратной связи и передаточную функции прямой цепи
Системы управления химико-технологическим процессами
Слайд 25Вопрос №10
Изображение выходного сигнала
Изображение входного сигнала
Дифференциальное уравнение, описывающее систему
Комплексная передаточная
функция
Передаточная функция
Уравнение Эйлера
Системы управления химико-технологическим процессами
Слайд 26Типовые динамические звенья САР
Системы управления химико-технологическим процессами
Слайд 27Безинерционные (усилительные или статические) звенья
К безинерционным звеньям относят элементы, которые
в динамике описываются дифференциальным уравнением нулевого порядка вида
yвых(t) = kхвх(t)
yвых(p)
= kxвх(p)
Из передаточной функции найдем статический коэффициент передачи звена
Системы управления химико-технологическим процессами
Слайд 28Из передаточной функции находят переходную и весовую функции в операторной
форме
Оригинал переходной характеристики находят из таблиц преобразования Лапласа.
Системы управления химико-технологическим
процессами
Слайд 29Весовая функция в операторной форме
ω(p)=W(p)
Оригинал весовой функции
ω(t) =
L-1 {k } = k (t)
Системы управления химико-технологическим процессами
Слайд 30Частотные характеристики звена найдем из выражения комплексной передаточной функции:
Амплитудно-частотная и
фазо-частотная характеристики звена имеют вид:
АЧХ:
ФЧХ:
Системы управления химико-технологическим процессами
Слайд 31Инерционное звено первого порядка
В динамике описывается дифференциальным уравнением первого порядка,
которое может быть приведено к виду:
где T - постоянная
времени звена;
k – статический коэффициент передачи звена;
В операторной форме уравнение имеет вид:
Т py(p) + y(p) = kx(p)
Системы управления химико-технологическим процессами
Слайд 32Передаточная функция находится как
Системы управления химико-технологическим процессами
Слайд 33
Весовая функция инерционного звена первого порядка в операторной форме
Частные характеристики
звена находим из выражения К(j)
Системы управления химико-технологическим процессами
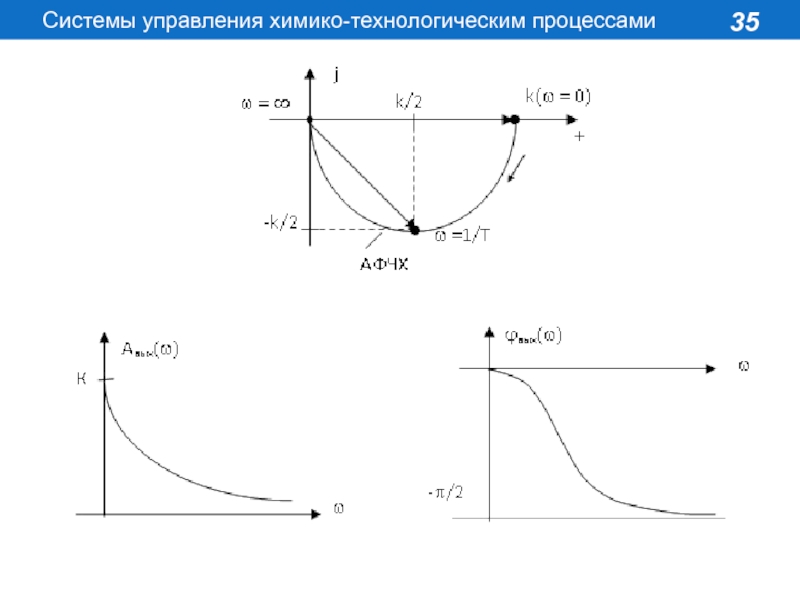
Слайд 34Амплитудно-частотную и фазо-частотную характеристи находим следующим образом
вых(w) = arg K(j)
= – arctg
Системы управления химико-технологическим процессами
Слайд 35Системы управления химико-технологическим процессами
Слайд 36Идеальное дифференцирующее звено
Дифференциальное уравнение звена
Уравнение в операторной форме
yвых(р) = kpxвх(p)
Передаточная
функция:
Системы управления химико-технологическим процессами
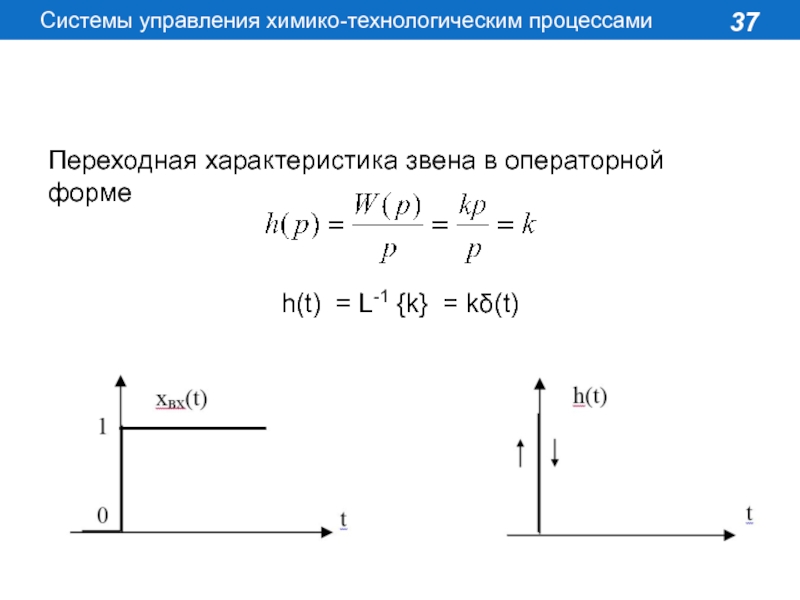
Слайд 37Переходная характеристика звена в операторной форме
h(t) = L-1 {k} =
k(t)
Системы управления химико-технологическим процессами
Слайд 38Частотные характеристики звена определим из выражения K(j)
АЧХ: Aвых() = K(j)Aвх=1
= k ,
ФЧХ: вых() = arg K(j) = +/2,
дифференцирующее звено вносит в систему опережение по фазе, равное 90о
Системы управления химико-технологическим процессами
Слайд 39Идеальное интегрирующее звено
Дифференциальное уравнение звена
pyвых(p) = kxвх(p)
Системы управления химико-технологическим процессами
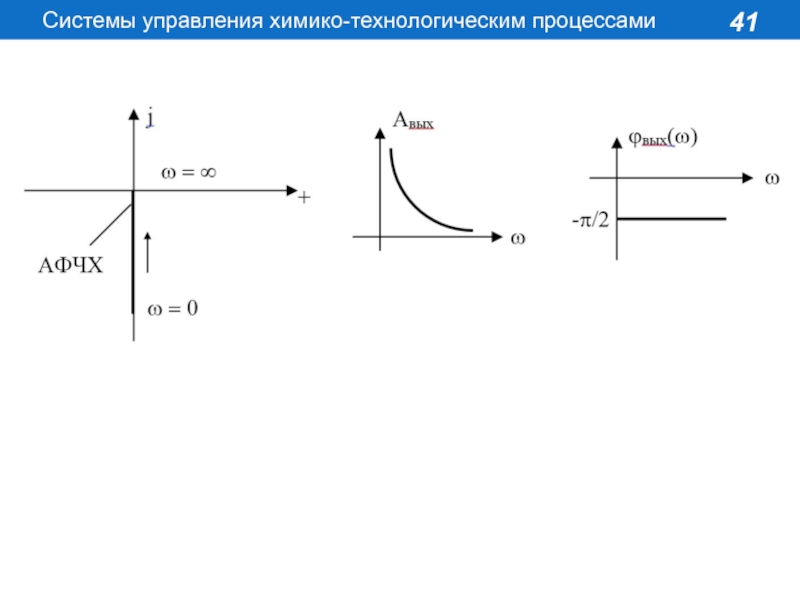
Слайд 40Переходная характеристика в операторной форме
Частотные характеристики звена определяются из
Системы управления
химико-технологическим процессами
Слайд 41Системы управления химико-технологическим процессами
Слайд 42Инерциальное звено второго порядка. Колебательное звено
Дифференциальное уравнение инерционного звена второго
порядка
в операторной форме:
Т22p2yвых(p) + T1pyвых(p) + yвых(p) = kxвх(p)
Передаточная функция:
Системы
управления химико-технологическим процессами
Слайд 43Системы управления химико-технологическим процессами
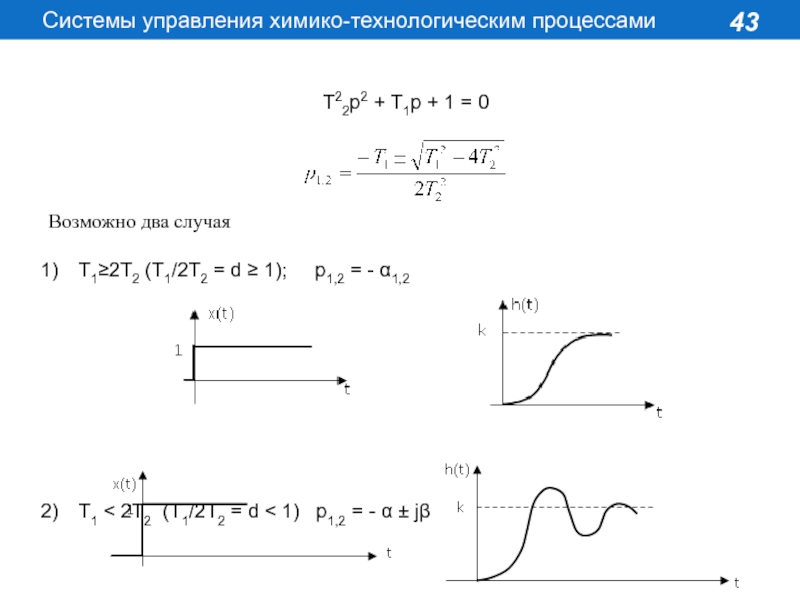
Т22p2 + T1p + 1 = 0
Возможно
два случая
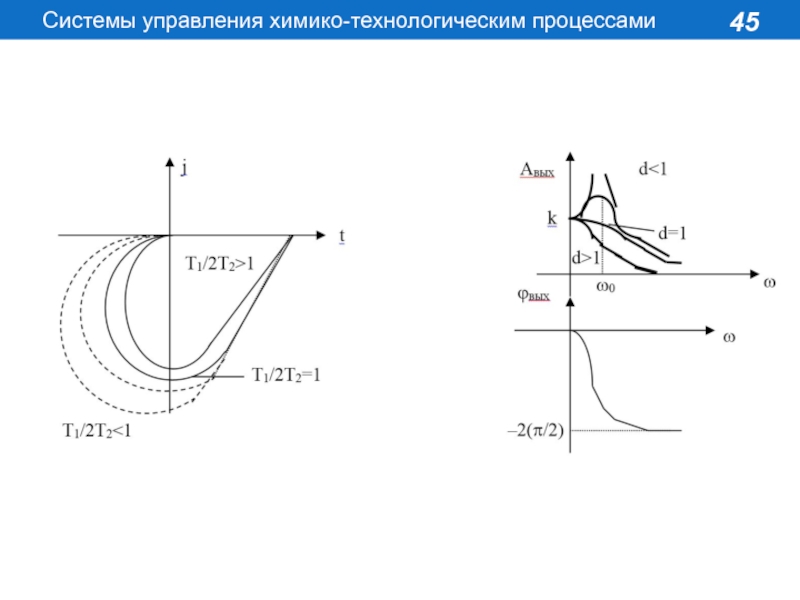
Т12Т2 (Т1/2Т2 = d 1); p1,2
= - 1,2
T1 < 2T2 (T1/2T2 = d < 1) p1,2 = - j
Слайд 44Системы управления химико-технологическим процессами
Частотные характеристики звена определяются из комплексной передаточной
функции
Слайд 45Системы управления химико-технологическим процессами
Слайд 46Системы управления химико-технологическим процессами
Слайд 47Устойчивость систем автоматического регулирования
Системы управления химико-технологическим процессами
Слайд 48Физическое и математическое определение устойчивости
Система автоматического регулирования называется устойчивой,
если после снятия возмущающего воздействия, которое вывело её из состояния
равновесия, она вновь возвращается в состояние равновесия. Если система не возвращается в состояние равновесия после снятия возмущения, она неустойчива
Системы управления химико-технологическим процессами
Слайд 49Системы управления химико-технологическим процессами
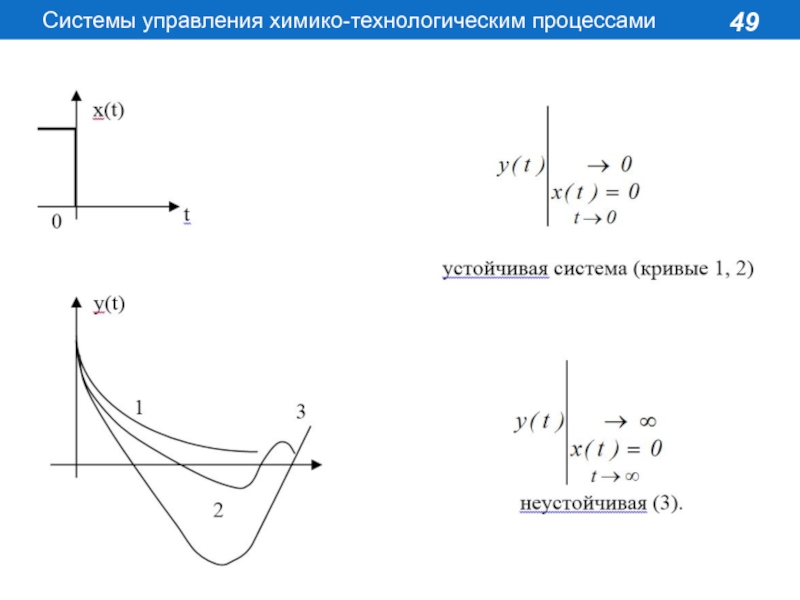
Слайд 50Для определения математического условия устойчивости САР необходимо решить дифференциальное уравнение
системы, когда правая часть этого уравнения равна 0 (при снятии
возмущающего воздействия), и посмотреть, как ведет yвых (t) при t .
αnpny(p) + ... + α1py(p) + αoy(p) = bmpmx(p) + ... + b1px(p) + box(p)
Для определения устойчивости системы, описываемой этим уравнением, снимем возмущения x(t)=0
Системы управления химико-технологическим процессами
Слайд 51Системы управления химико-технологическим процессами
Для этого запишем характеристическое уравнение:
H(p) = αnpn
+ .... + α1p + αo = 0.
Как видно
из последнего выражения, характеристическое уравнение звена или системы – это знаменатель передаточной функции звена или системы, приравненный к нулю.
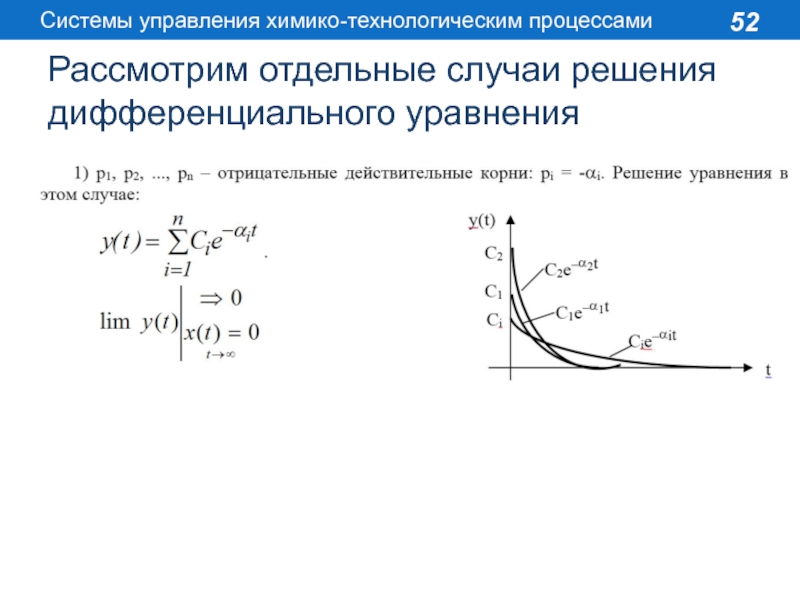
Если p1, p2, ..., pn – корни характеристического уравнения, то решение этого уравнения имеет вид:
Слайд 52Рассмотрим отдельные случаи решения дифференциального уравнения
Системы управления химико-технологическим процессами
Слайд 53Системы управления химико-технологическим процессами
Слайд 54Системы управления химико-технологическим процессами
Слайд 55Системы управления химико-технологическим процессами
Слайд 56Анализируя все случаи решения дифференциального уравнения для случая x(t) =
0, можно сделать вывод: система автоматического регулирования устойчива, если все
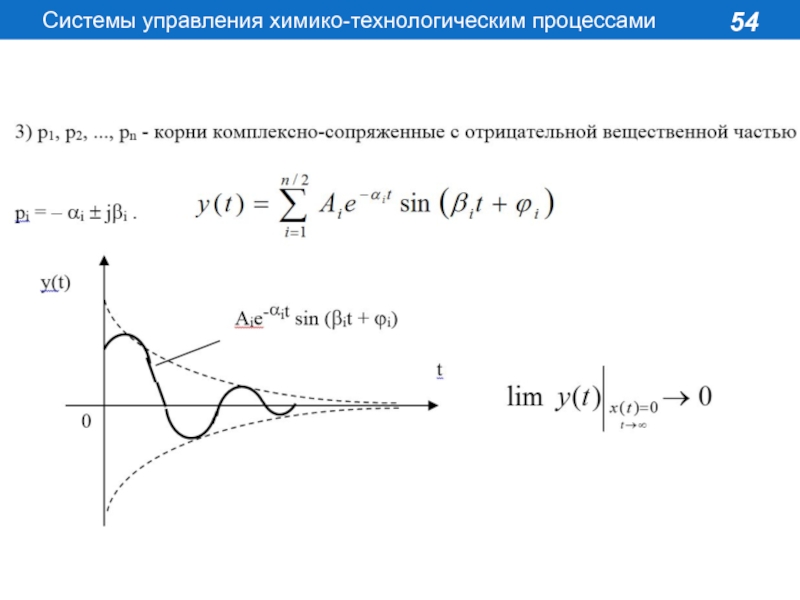
корни ее характеристического уравнения отрицательные действительные или комплексно-сопряженные с отрицательной действительной частью.
Если же среди корней характеристического уравнения системы имеется хотя бы один положительный действительный корень или хотя бы одна пара комплексно-сопряженных корней с положительной вещественной частью, такая система неустойчива.
Математические правила, позволяющие определить знаки корней алгебраического (характеристического) уравнения, не решая это уравнение, в ТАУ называют критериями устойчивости.
Системы управления химико-технологическим процессами
Слайд 57Алгебраический критерий Гурвица
Алгебраические критерии устойчивости позволяют судить об устойчивости системы
по коэффициентам характеристического уравнения.
Система автоматического регулирования устойчива, если все коэффициенты
её характеристического уравнения имеют одинаковые знаки, а главный диагональный определитель системы (определитель Гурвица) и его диагональные миноры будут положительными.
Системы управления химико-технологическим процессами
Слайд 58Системы управления химико-технологическим процессами
Необходимые условия: α0 > 0, α1 >
0,……, αn 0 или α0
условия, составляют из коэффициентов уравнения главный диагональный определитель:
по главной диагонали определителя слева направо выписывают все коэффициенты характеристического уравнения, начиная со второго.
столбцы вверх от главной диагонали дополняют коэффициенты с последовательно убывающими индексами;
столбцы вниз – коэффициентами с последовательно возрастающими индексами;
iый диагональный минор получают отчёркивая iый столбец и iую строку.
Слайд 59Частотный критерий Михайлова
Системы управления химико-технологическим процессами
Частотные критерии устойчивости позволяют судить
об устойчивости систем автоматического управления по виду их частотных характеристик.
Пусть характеристическое уравнение системы имеет вид:
Заменив в Н(р) оператор р на оператор jω, получим вектор Н(jω)
Пусть p1, p2,......, pn - корни характеристического уравнения. Тогда в соответствии с теоремой Безу характеристическое уравнение можно переписать в виде:
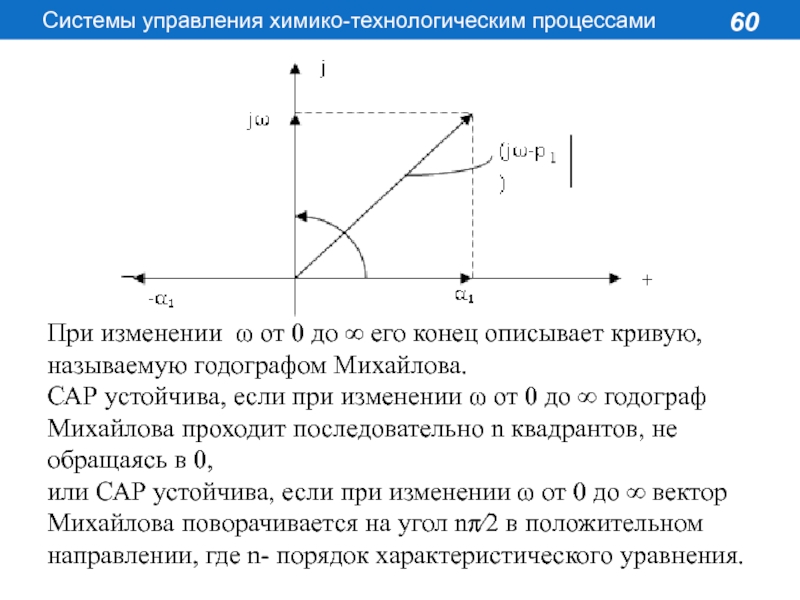
Величина (jω-pj) геометрически изображается векторами в комплексной плоскости, а Н(jω) представляет собой вектор, равный произведению элементарных векторов (jω-pi), модуль этого вектора равен произведению модулей элементарных векторов, а фаза – сумма фаз элементарных векторов.
Условимся считать вращение против часовой стрелки положительным, тогда при изменении ω от 0 до ∞ каждый элементарный вектор повернется на некоторый угол.
Слайд 60Системы управления химико-технологическим процессами
При изменении ω от 0 до ∞
его конец описывает кривую, называемую годографом Михайлова.
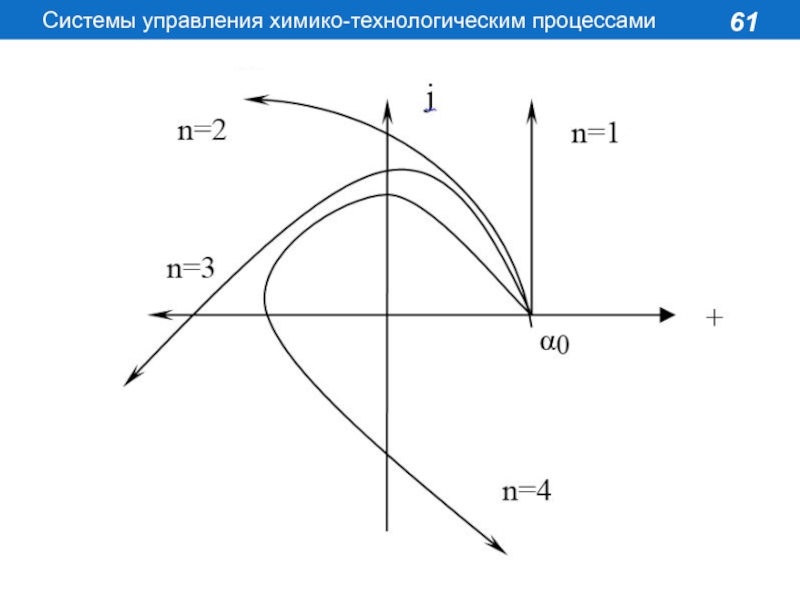
САР устойчива, если при
изменении ω от 0 до ∞ годограф Михайлова проходит последовательно n квадрантов, не обращаясь в 0,
или САР устойчива, если при изменении ω от 0 до ∞ вектор Михайлова поворачивается на угол nπ⁄2 в положительном направлении, где n- порядок характеристического уравнения.
Слайд 61Системы управления химико-технологическим процессами
Слайд 62Системы управления химико-технологическим процессами
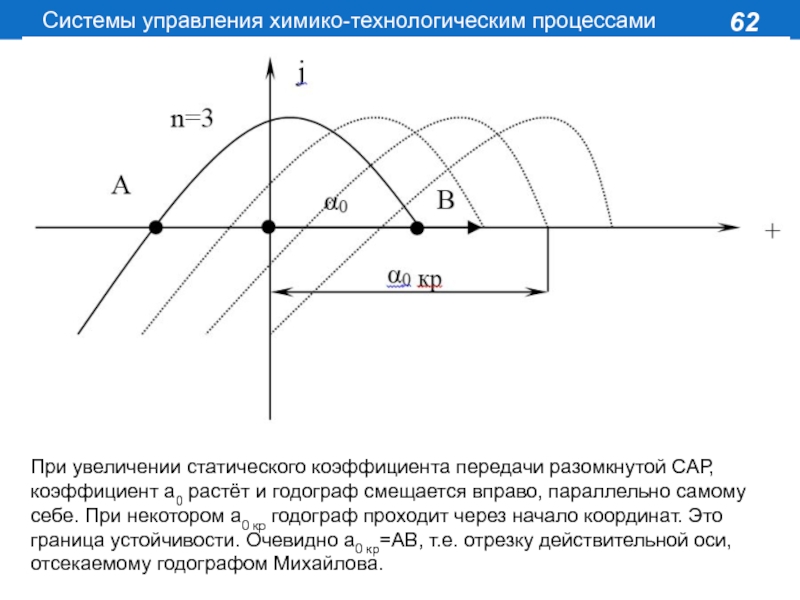
При увеличении статического коэффициента передачи разомкнутой САР,
коэффициент а0 растёт и годограф смещается вправо, параллельно самому себе.
При некотором а0 кр годограф проходит через начало координат. Это граница устойчивости. Очевидно а0 кр=АВ, т.е. отрезку действительной оси, отсекаемому годографом Михайлова.
Слайд 63Частотный критерий Найквиста
Этот критерий позволяет судить об устойчивости замкнутых САР
по амплитудно-фазовой характеристике разомкнутой САР.
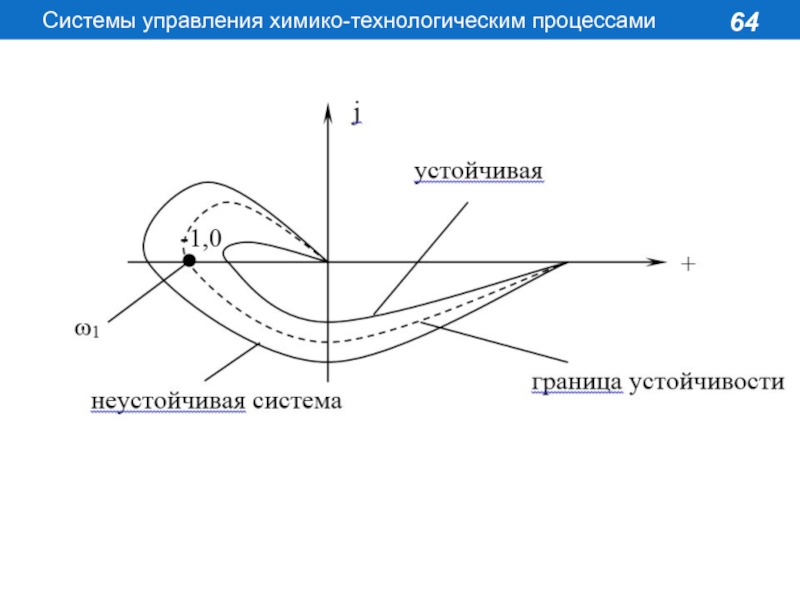
Замкнутая САР устойчива, если устойчива разомкнутая
САР и её АФЧХ не охватывает точки с координатами (-1, j0)
Пусть Wраз=N(p)/M(p), тогда К(jω)раз=N(jω)/M(jω) - выражение для АФЧХ. Построим АФЧХ разомкнутой САР
Системы управления химико-технологическим процессами
Слайд 64Системы управления химико-технологическим процессами
Слайд 65Благодарю за внимание
Сергей Степанович Погляд
SPoglyad@yandex.ru
http://vk.com/poglyad
https://www.facebook.com/sergey.poglyad