Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сложение и вычитание векторов Л.С. Атанасян "Геометрия 7-9" Савченко Е.М.,
Содержание
- 1. Сложение и вычитание векторов Л.С. Атанасян "Геометрия 7-9" Савченко Е.М.,
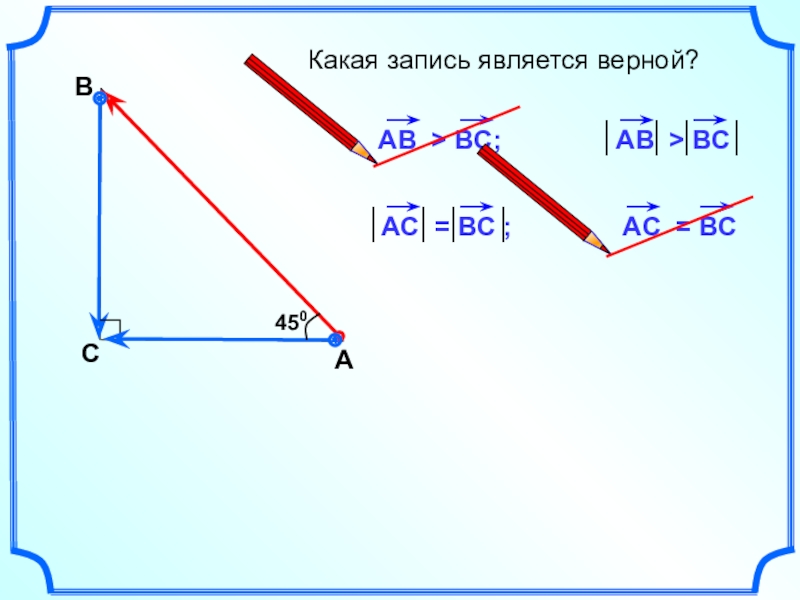
- 2. АВСКакая запись является верной?450
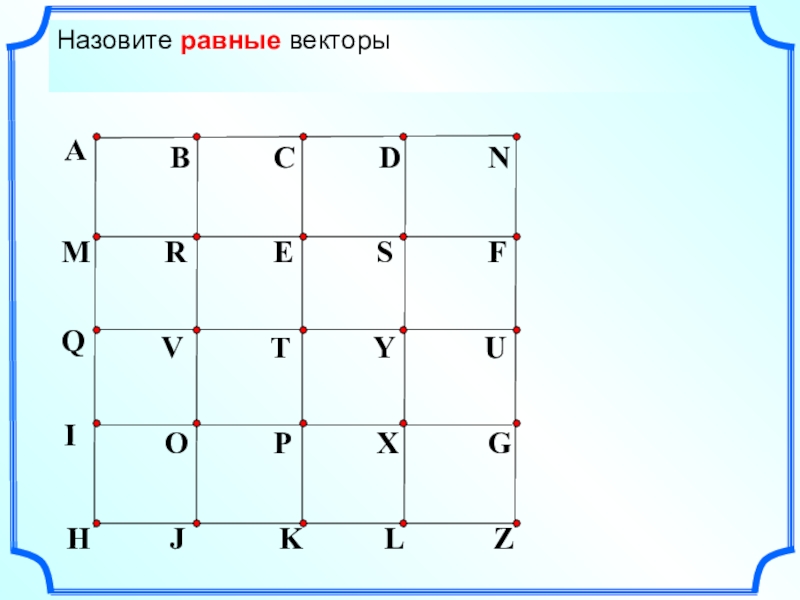
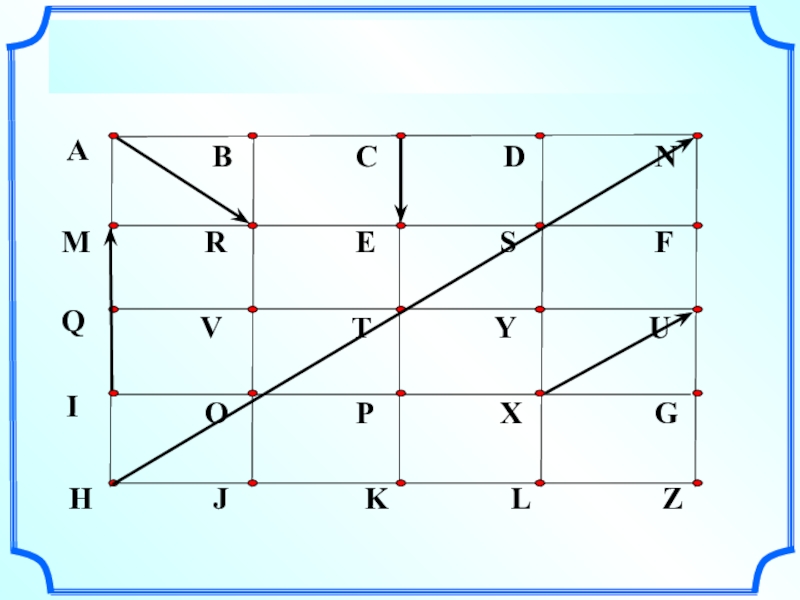
- 3. Назовите коллинеарные сонаправленные векторыНазовите коллинеарные противоположнонаправленные векторыНазовите равные векторы
- 4. Назовите коллинеарные сонаправленные векторыНазовите коллинеарные противоположнонаправленные векторы
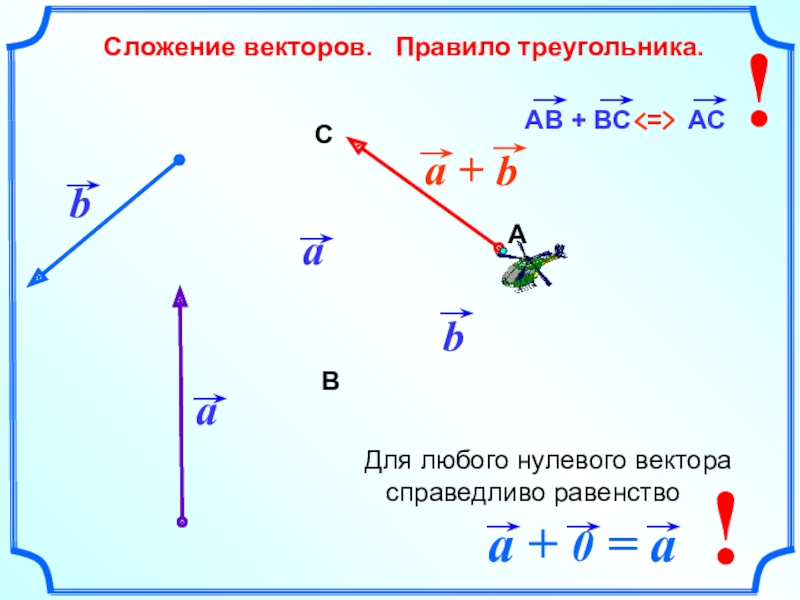
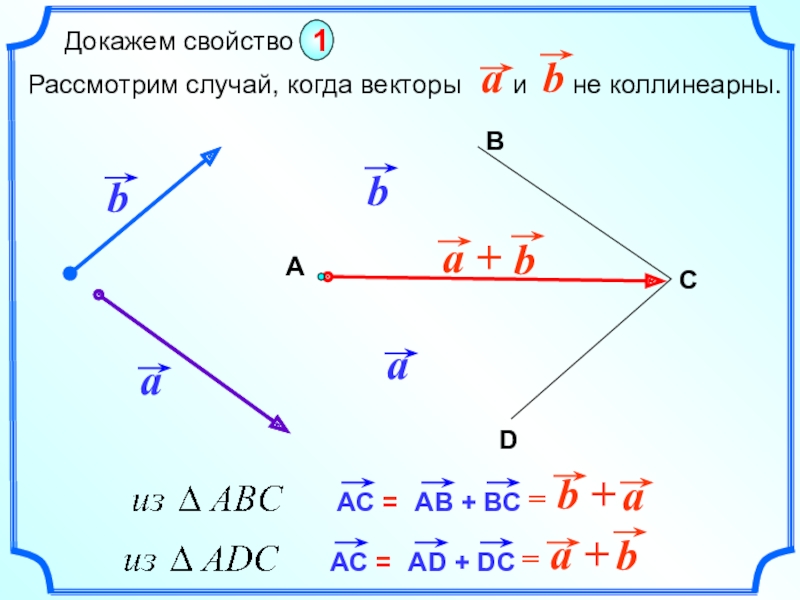
- 5. Сложение векторов. Правило треугольника.bАВС!! Для любого нулевого вектора справедливо равенство
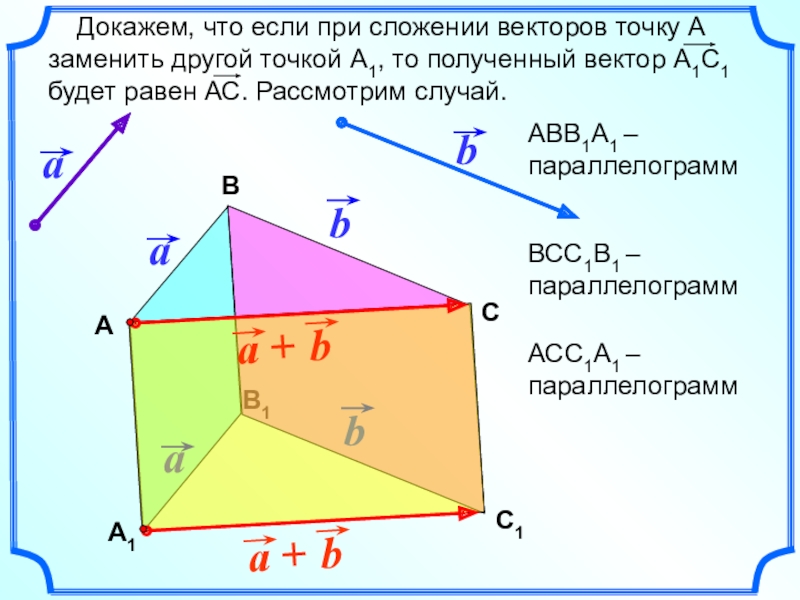
- 6. В1 Докажем, что если при сложении
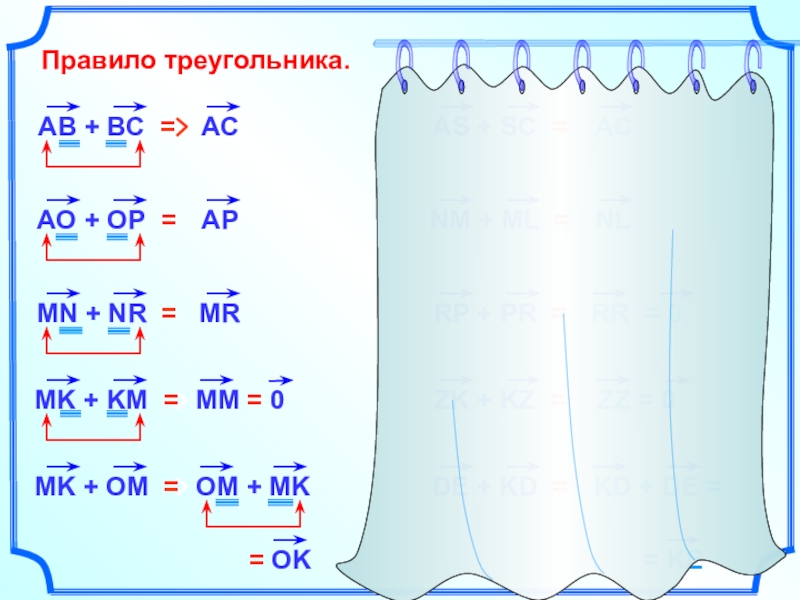
- 7. Правило треугольника.RR = 0
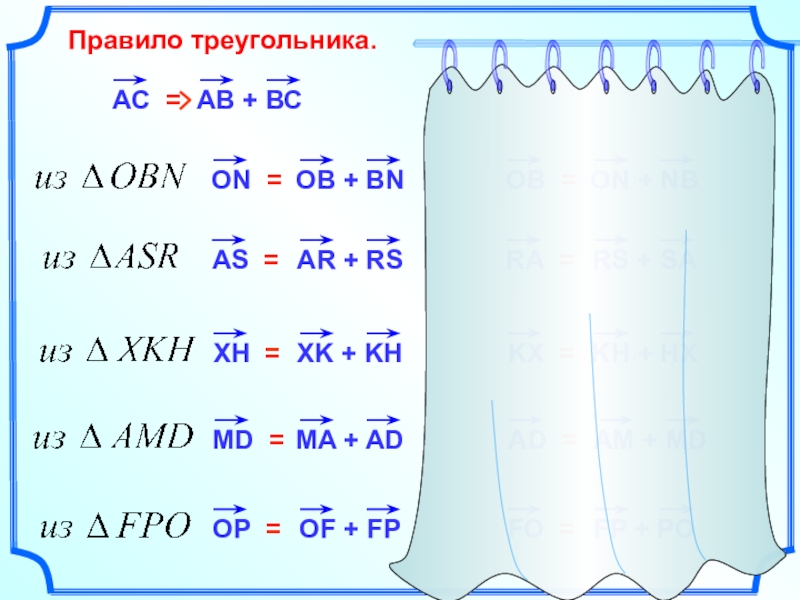
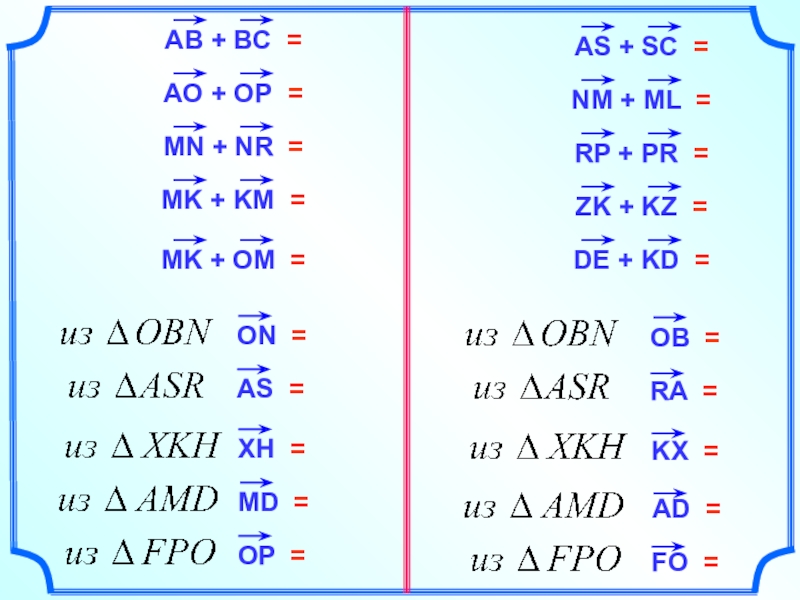
- 8. Правило треугольника.АС =OB =RA =KX =AD =FO =
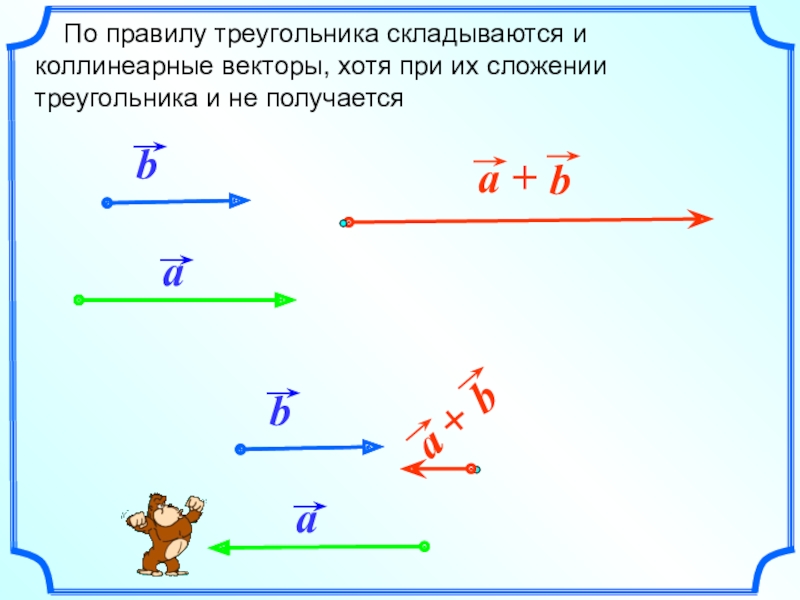
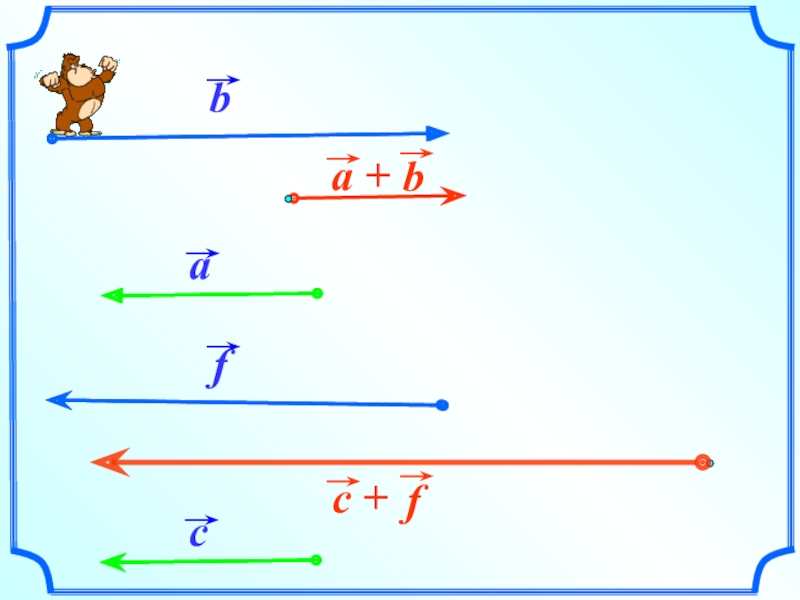
- 9. По правилу треугольника складываются и
- 10. Слайд 10
- 11. Законы сложения векторовДля любых векторов
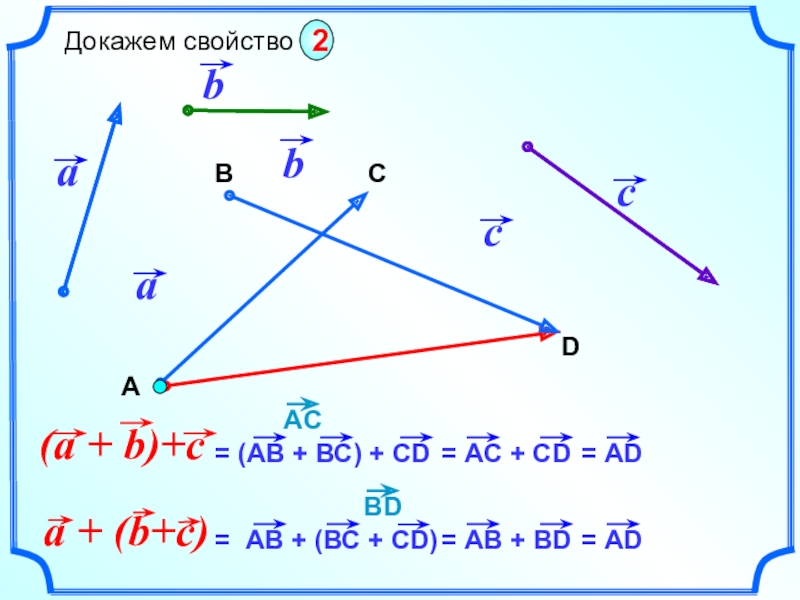
- 12. АВDC
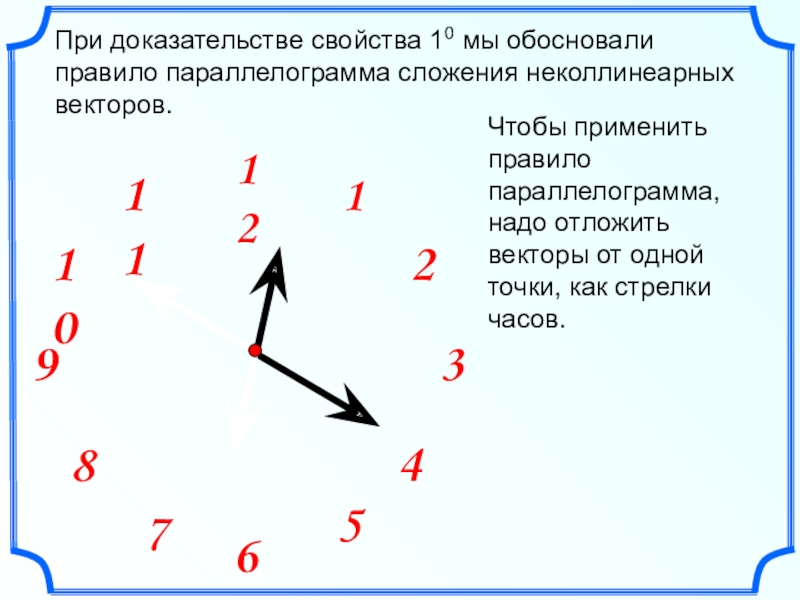
- 13. При доказательстве свойства 10 мы обосновали правило
- 14. Сложение векторов. Правило параллелограмма.
- 15. ВDC Докажем свойство2А
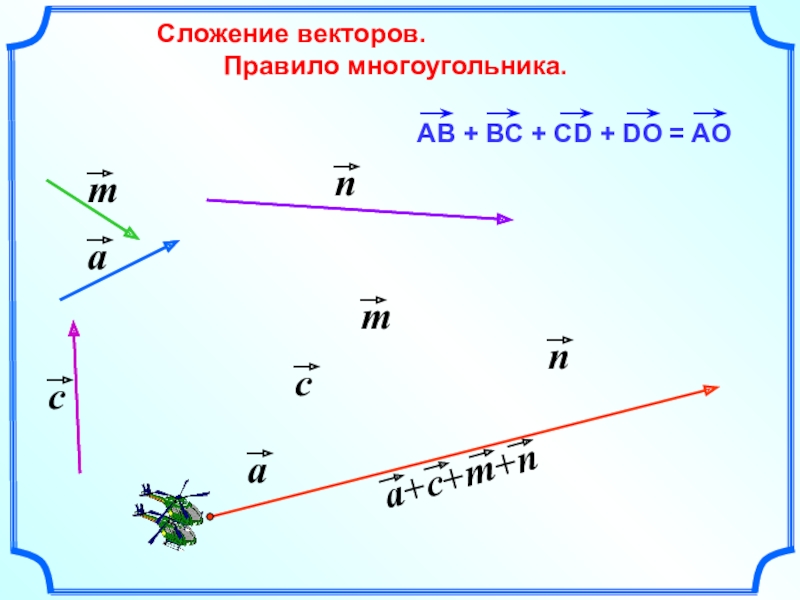
- 16. Сложение векторов. Правило многоугольника.
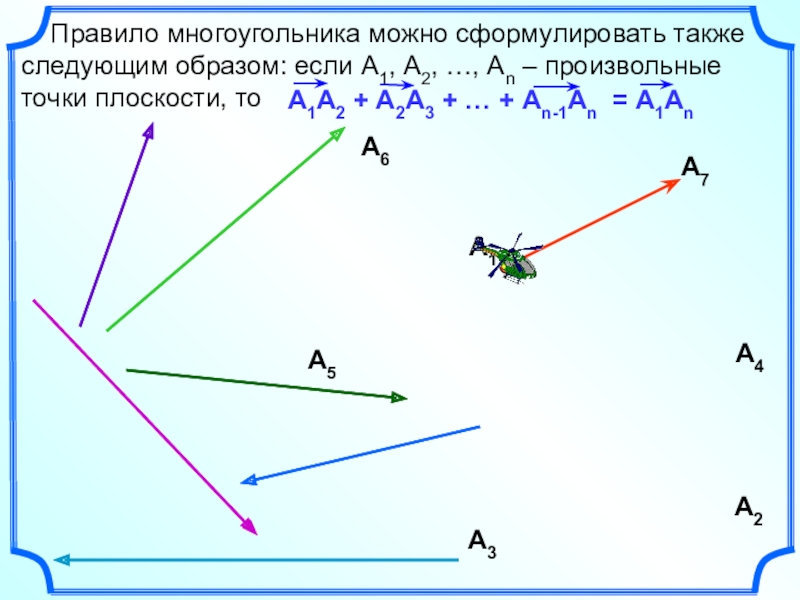
- 17. Правило многоугольника можно сформулировать также
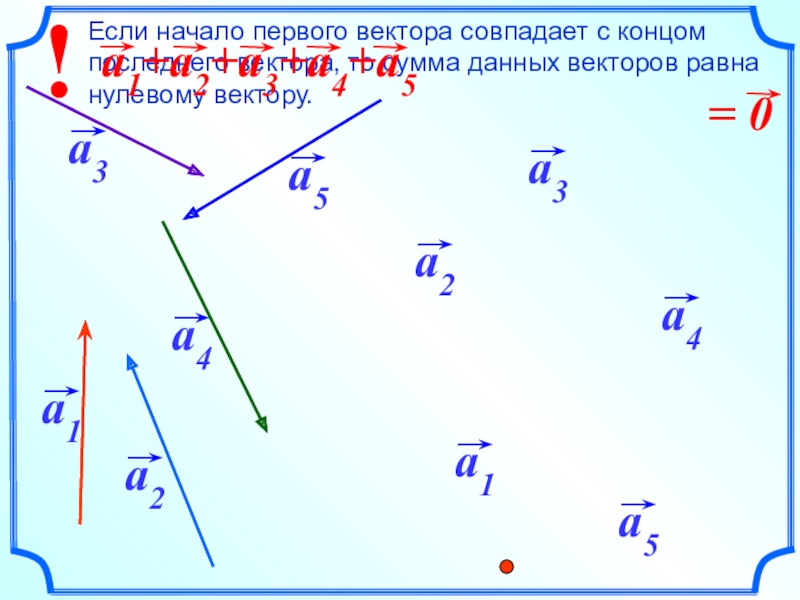
- 18. Слайд 18
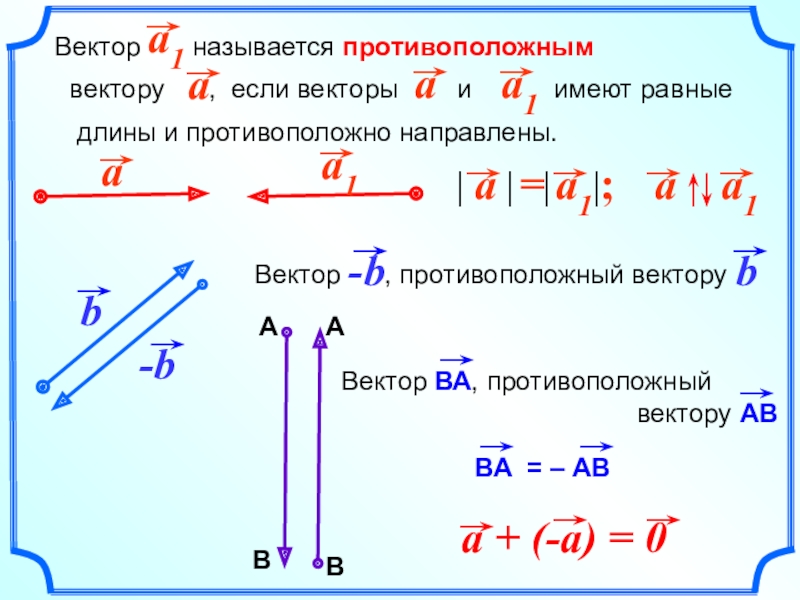
- 19. Вектор называется противоположным
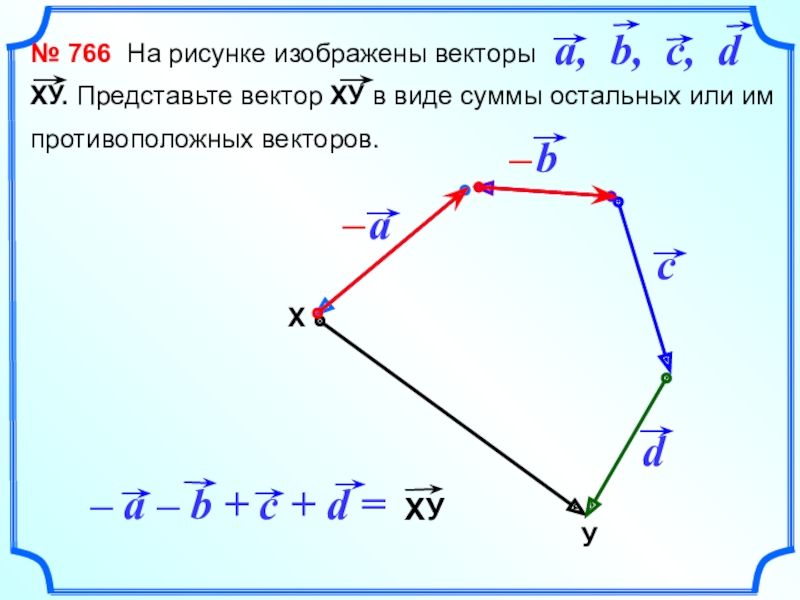
- 20. № 766 На рисунке изображены
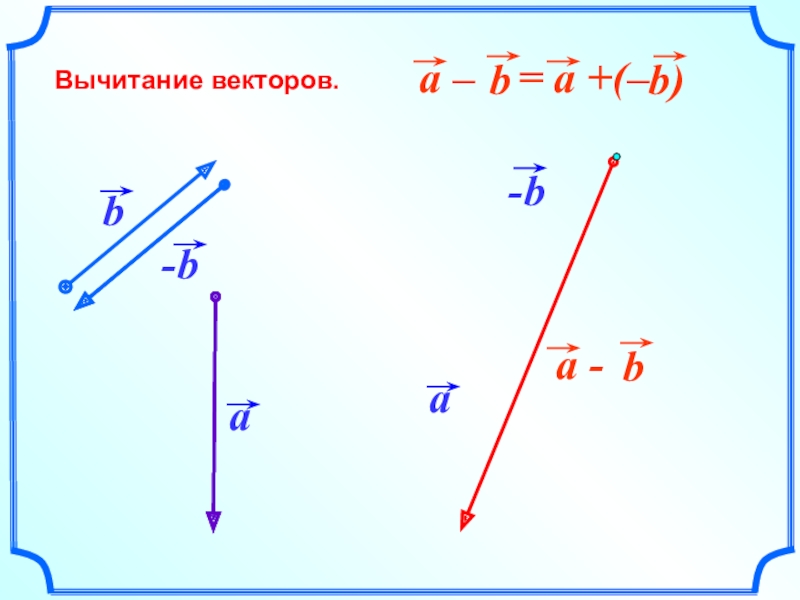
- 21. Вычитание векторов.
- 22. Вычитание векторов.
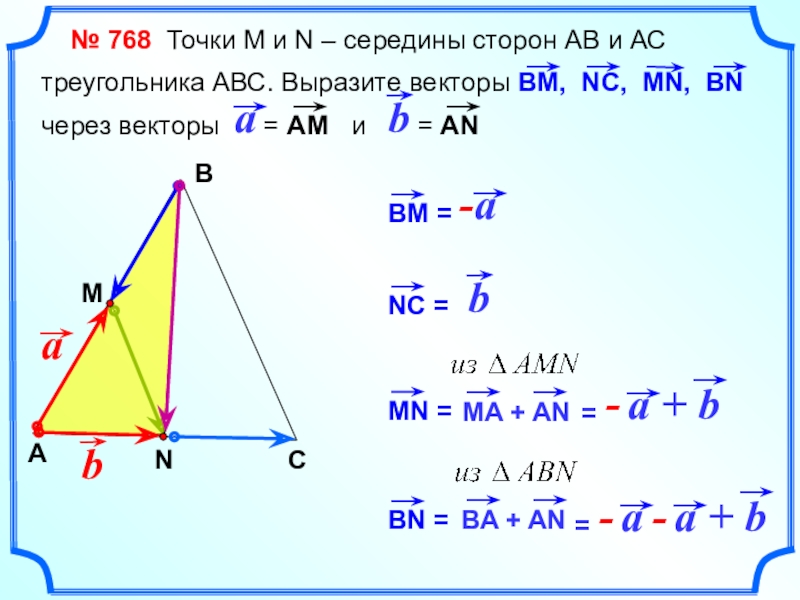
- 23. № 768 Точки М и
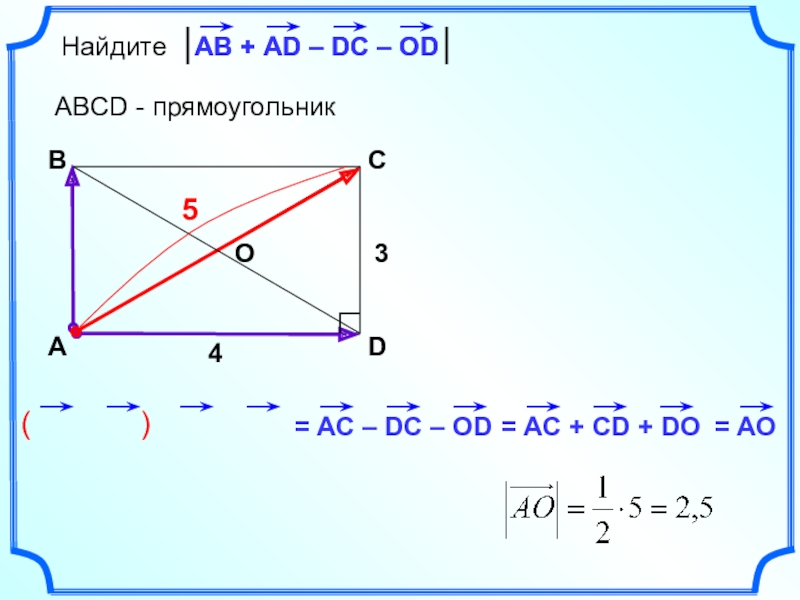
- 24. ( )НайдитеABCD - прямоугольникАBCDАВ + AD – DC – ODО345
- 25. Слайд 25
- 26. Скачать презентанцию
АВСКакая запись является верной?450
Слайды и текст этой презентации
Слайд 3Назовите коллинеарные сонаправленные векторы
Назовите коллинеарные противоположнонаправленные векторы
Назовите равные векторы
Слайд 4Назовите коллинеарные сонаправленные векторы
Назовите коллинеарные противоположнонаправленные векторы
Слайд 5 Сложение векторов. Правило треугольника.
b
А
В
С
!
!
Для любого
нулевого вектора справедливо равенство
Слайд 6В1
Докажем, что если при сложении векторов точку А
заменить другой точкой А1, то полученный вектор А1С1
будет равен АС.
Рассмотрим случай. В
С
С1
АВВ1А1 – параллелограмм
ВСС1В1 – параллелограмм
АСС1А1 – параллелограмм
Слайд 9 По правилу треугольника складываются и коллинеарные векторы, хотя
при их сложении треугольника и не получается
Слайд 13При доказательстве свойства 10 мы обосновали правило параллелограмма сложения неколлинеарных
векторов.
Чтобы применить правило параллелограмма, надо отложить векторы от одной точки,
как стрелки часов. Слайд 17 Правило многоугольника можно сформулировать также следующим образом: если
А1, А2, …, Аn – произвольные точки плоскости, то
= А1An
А1А2
+ А2А3 + … + Аn-1An А2
А3
А4
А5
А6
А7
А1
Слайд 19Вектор называется противоположным
вектору
, если векторы и
имеют равныедлины и противоположно направлены.
Слайд 20 № 766 На рисунке изображены векторы
ХУ.
Представьте вектор ХУ в виде суммы остальных или им
противоположных векторов.У
Х
–
–
Слайд 23 № 768 Точки М и N – середины
сторон АВ и АС
треугольника АВС. Выразите векторы ВМ, NC,
MN, BN через векторы = АМ и = АN
С
-
-
В
А