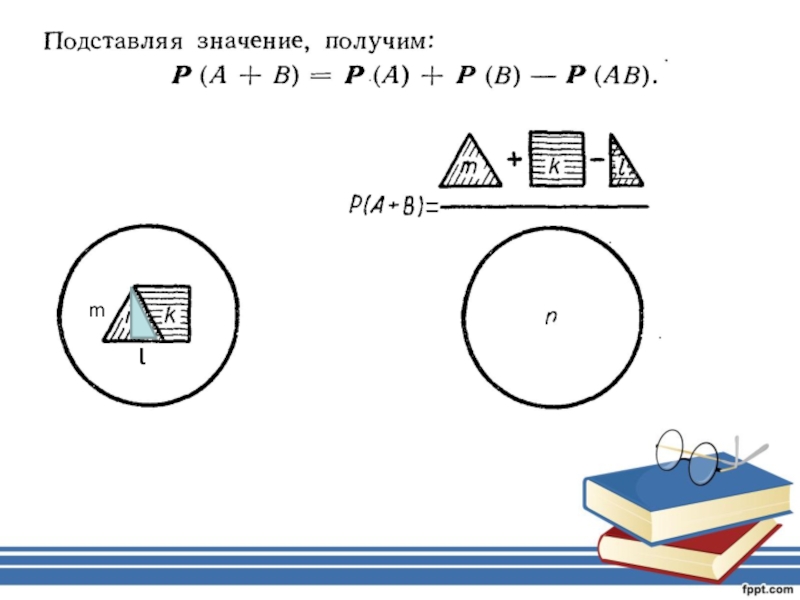
ящике находится красный, черный и белый шары.
А- извлечение черного шараВ- извлечение красного шара
С- извлечение белого шара
А+В – извлечен черный или красный шар
В+С – извлечен красный или белый шар
А+С – извлечен черный или белый шар
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.