величины возникает в программировании очень часто. К примеру, входные данные
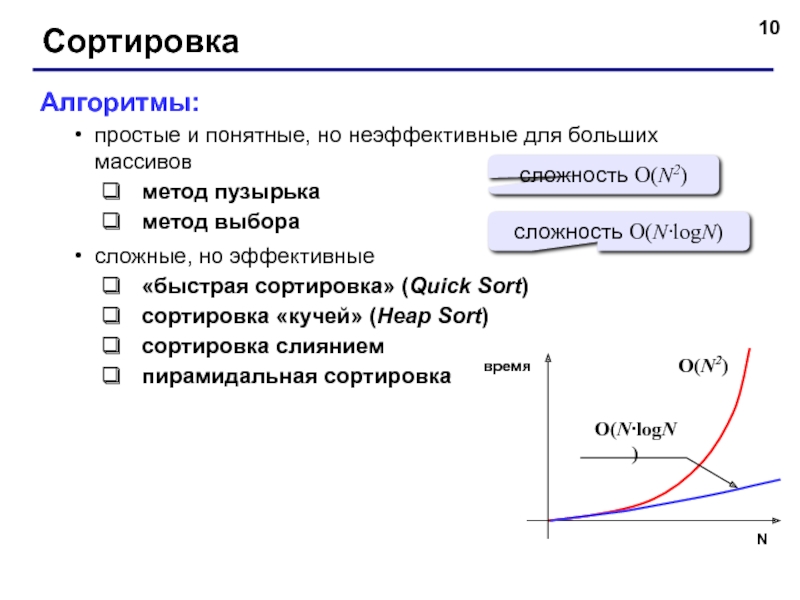
подаются "вперемешку", а вашей программе удобнее обрабатывать упорядоченную последовательность.Существуют ситуации, когда предварительная сортировка данных позволяет сократить содержательную часть алгоритма в разы, а время его работы - в десятки раз.












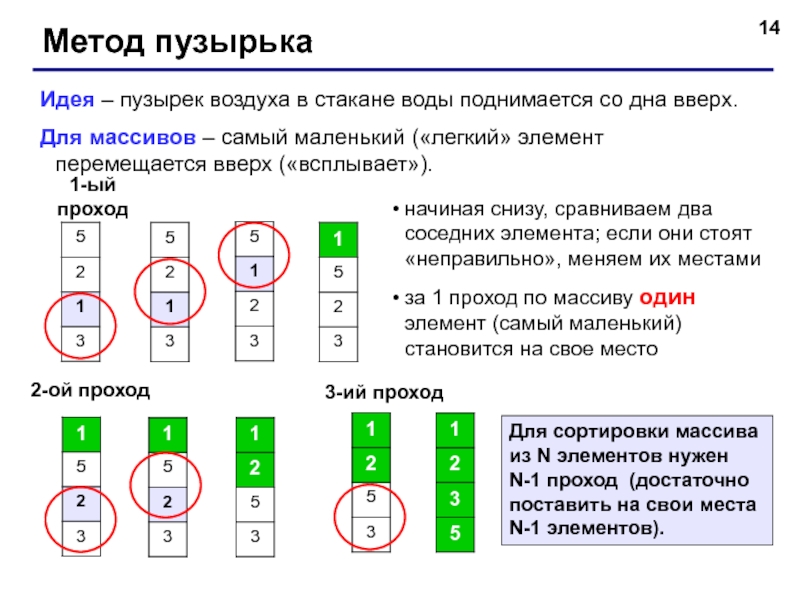
![Сортировка массивов Программа1-ый проход:сравниваются пары A[N-1] и A[N], A[N-2] и A[N-1] … A[1] Программа1-ый проход:сравниваются пары A[N-1] и A[N], A[N-2] и A[N-1] … A[1] и A[2] A[j] и A[j+1]2-ой](/img/thumbs/73971ed99ba6e88aa4aecc5798aee2f3-800x.jpg)
![Сортировка массивов Программаprogram qq;const N = 10;var A: array[1..N] of integer; i, j, Программаprogram qq;const N = 10;var A: array[1..N] of integer; i, j, c: integer;begin { заполнить массив](/img/thumbs/2b13ef7737817ee4d4dccbf59952ce42-800x.jpg)

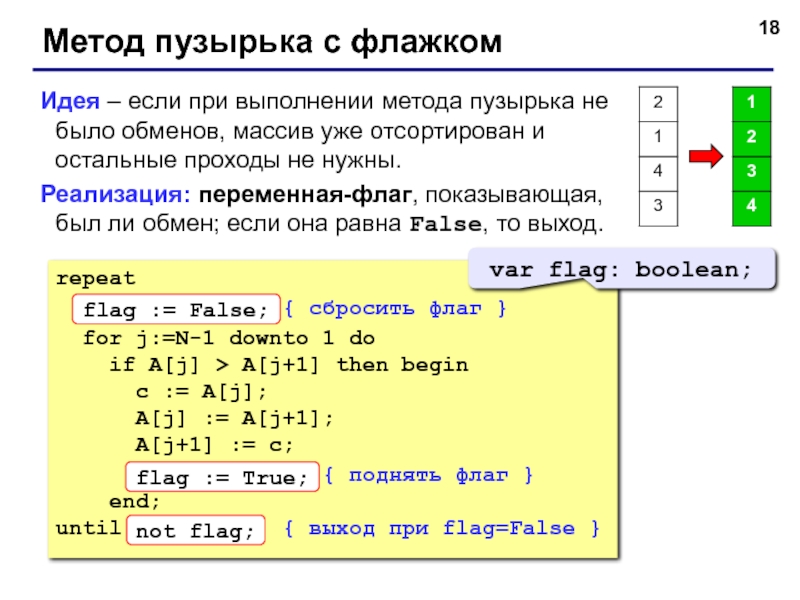
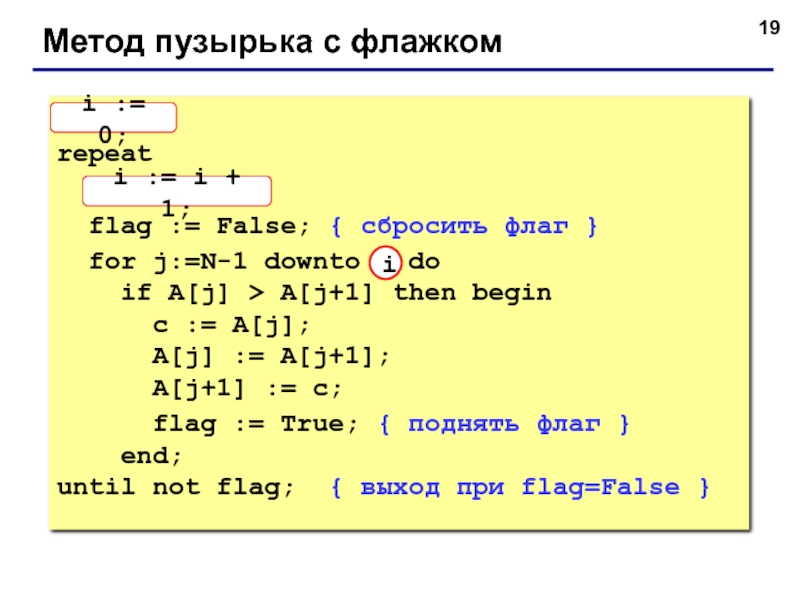
![Сортировка массивов Метод выбораИдея:найти минимальный элемент и поставить на первое место (поменять местами Метод выбораИдея:найти минимальный элемент и поставить на первое место (поменять местами с A[1])из оставшихся найти минимальный элемент](/img/thumbs/f20d589cd63d1ff3818ed62cb25cc555-800x.jpg)



![Сортировка массивов Фрагмент программы:Сортировка простыми вставкамиfor i:= 2 to N do if a[i-1]>a[i] Фрагмент программы:Сортировка простыми вставкамиfor i:= 2 to N do if a[i-1]>a[i] then begin](/img/thumbs/f22508b19fd9c8354d7def2d4cb502fe-800x.jpg)

![Сортировка массивов Фрагмент программы:for i:= 2 to N do if a[i-1]>a[i] then begin Фрагмент программы:for i:= 2 to N do if a[i-1]>a[i] then begin a[0]:= a[i]; {*}](/img/thumbs/6652a8e6f3994178a75765d0d4f46865-800x.jpg)

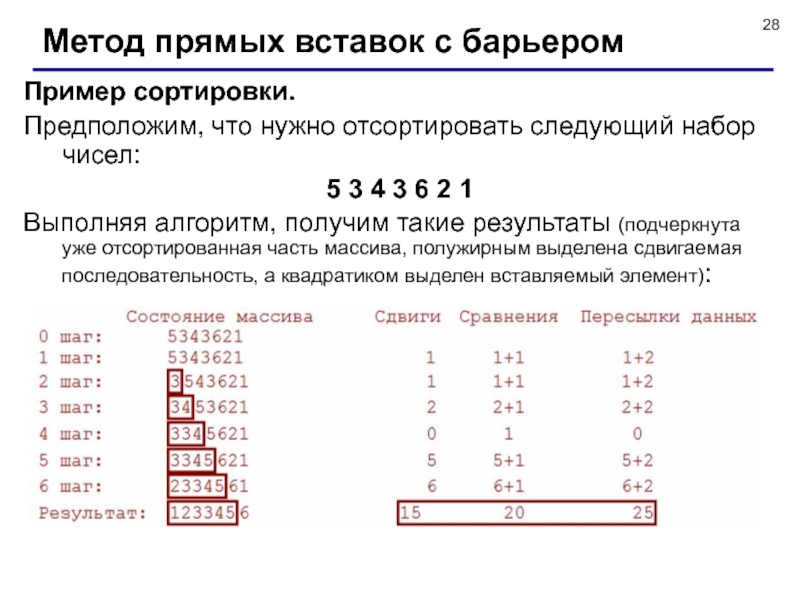






![Сортировка массивов Добавим число 21 в последовательность. 2 4 6 8 10 [12 Добавим число 21 в последовательность. 2 4 6 8 10 [12 14 16 18]2 4 6 8](/img/thumbs/eeac2c100f55681f774b2053d8f2a98e-800x.jpg)
![Сортировка массивов Фрагмент программы:for i:= 2 to n do if a[i-1]>a[i] then Фрагмент программы:for i:= 2 to n do if a[i-1]>a[i] then begin x:= a[i]; left:=](/img/thumbs/7c5ee8009e72a045745d83dc0cfad805-800x.jpg)





![Сортировка массивов Сортирует элементы массива А[1..n] следующим образом:на первом шаге упорядочиваются элементы n/2 Сортирует элементы массива А[1..n] следующим образом:на первом шаге упорядочиваются элементы n/2 пар (A[i], А[n/2 + i]) для](/img/thumbs/ebb14e26bc25019b961f9ce8d22b00ef-800x.jpg)
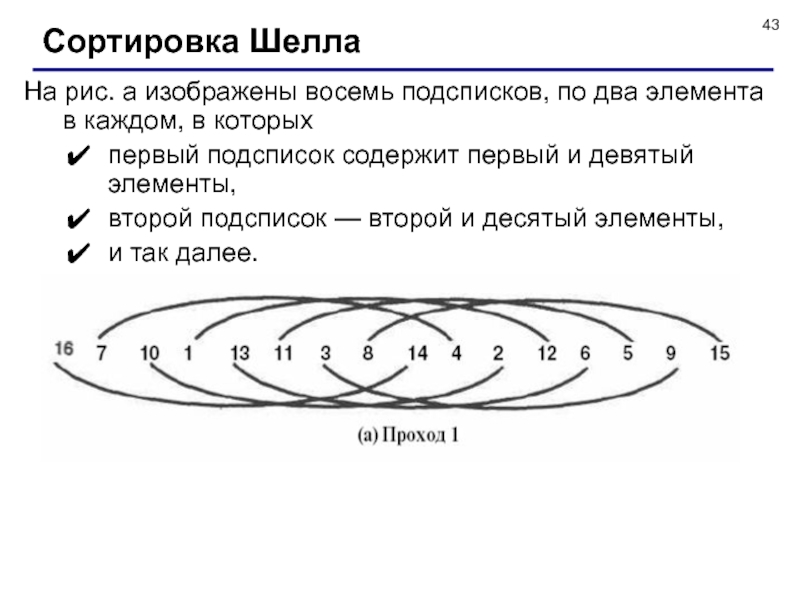
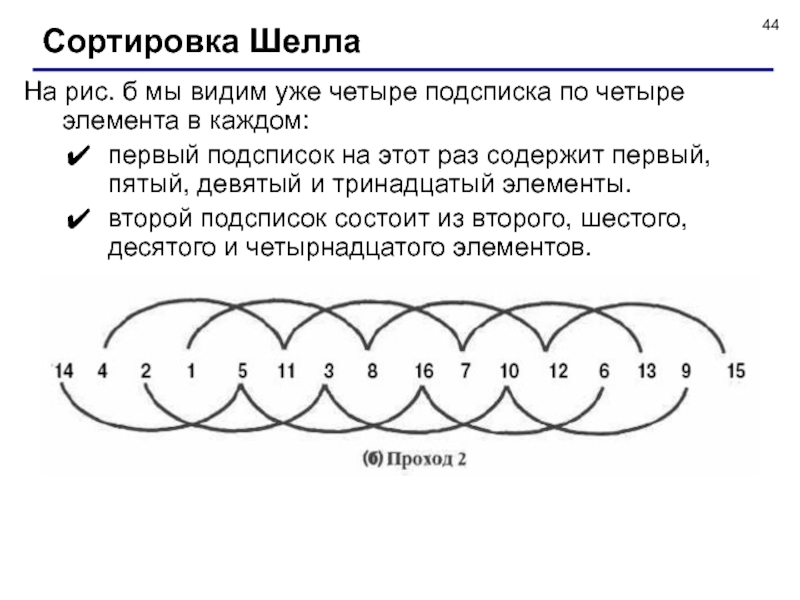


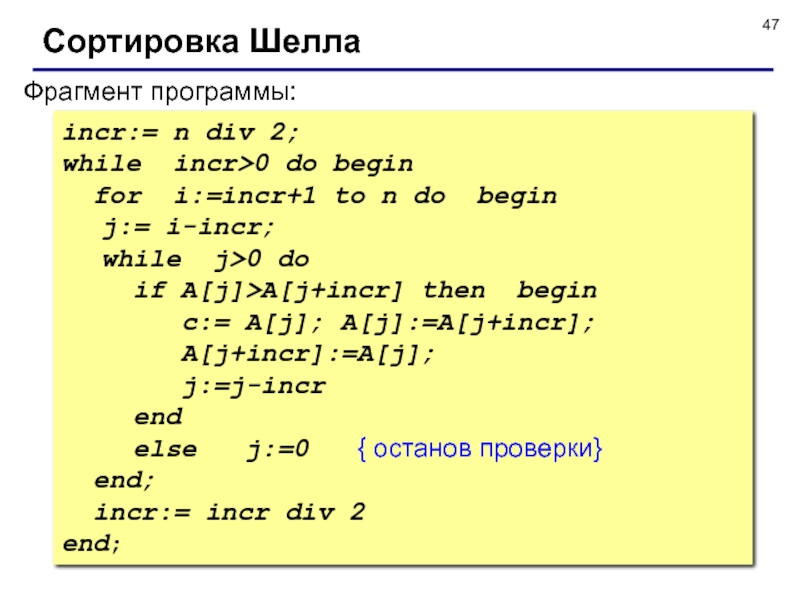



![Сортировка массивов Итак, будем рассматривать наш линейный массив как пирамидальную структуру: Видно, что любой элемент a[i] (1 Итак, будем рассматривать наш линейный массив как пирамидальную структуру: Видно, что любой элемент a[i] (1](/img/thumbs/e7fbf6d996b18eea727d5ddf5a95fd3c-800x.jpg)
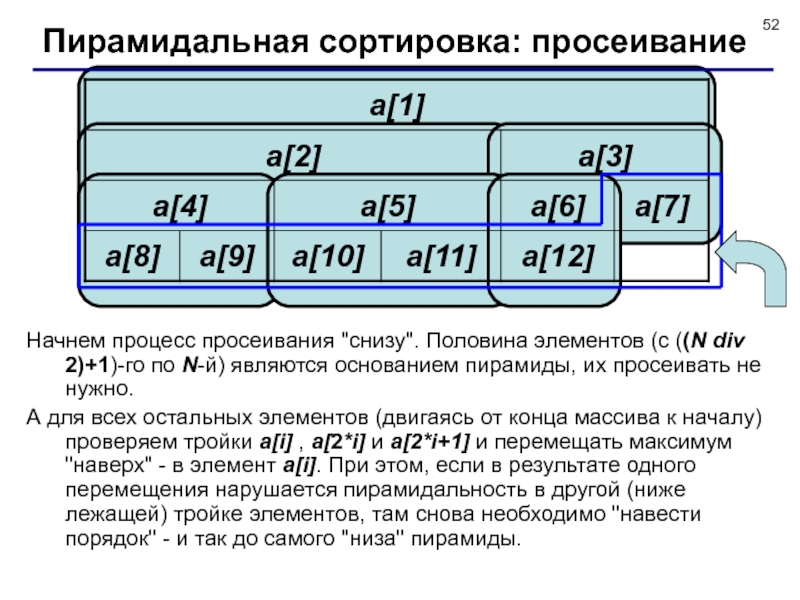

![Сортировка массивов Пример результата просеиванияВозьмем массив [1,7,5,4,9,8,12,11,2,10,3,6] (N = 12).Его исходное состояние таково Пример результата просеиванияВозьмем массив [1,7,5,4,9,8,12,11,2,10,3,6] (N = 12).Его исходное состояние таково (серым цветом выделено](/img/thumbs/391bfd02b5981af922f871f0f98c24d1-800x.jpg)

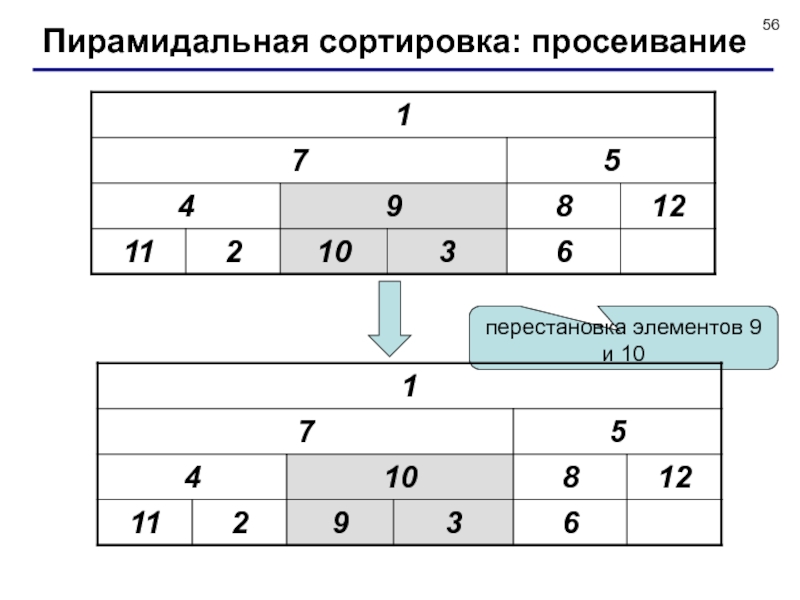


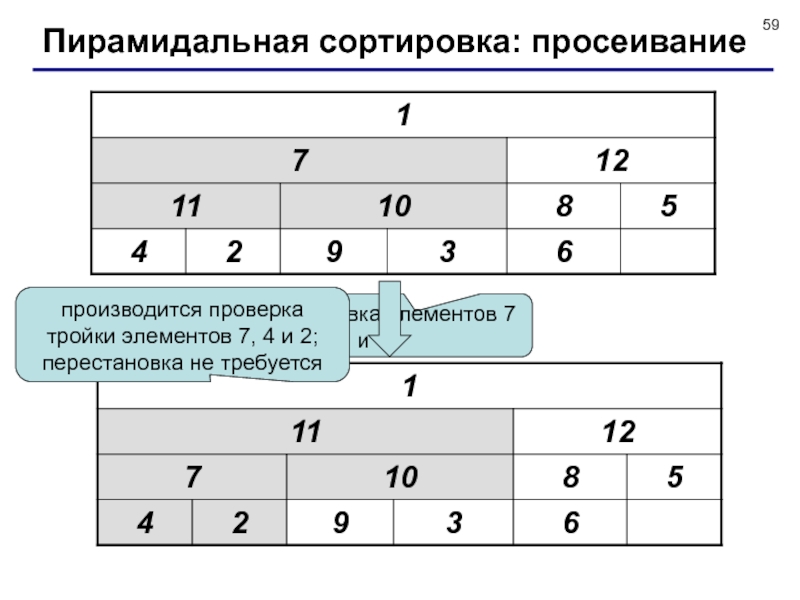
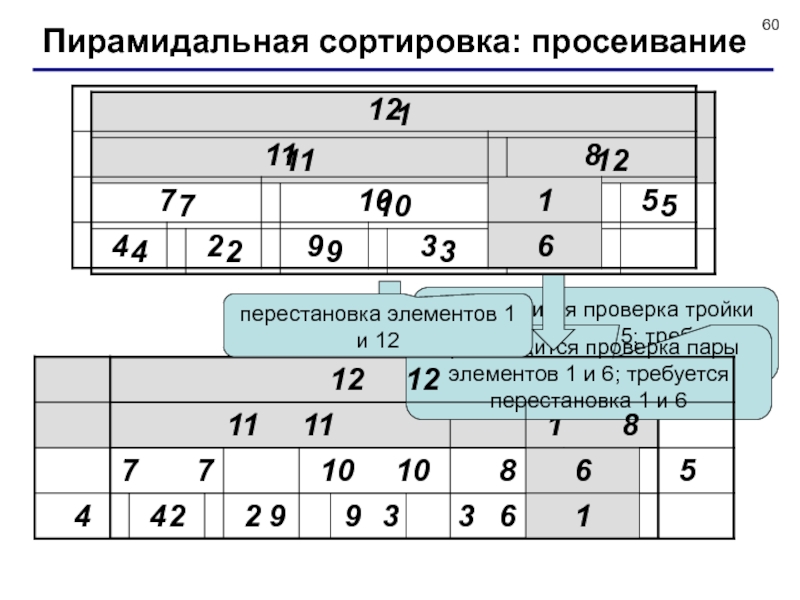
![Сортировка массивов Итак, мы превратили исходный массив в пирамиду: в любой тройке a[i], Итак, мы превратили исходный массив в пирамиду: в любой тройке a[i], a[2*i] и a[2*i+1] максимум находится](/img/thumbs/8ff7840d7912da758d6429ffae697d44-800x.jpg)



![Сортировка массивов 1) Меняем местами a[1] и a[12]: [1, 11, 8, 7, 10, 1) Меняем местами a[1] и a[12]: [1, 11, 8, 7, 10, 6, 5, 4, 2, 9, 3],](/img/thumbs/035caad7bd26107ab8927dc0ad330091-800x.jpg)
![Сортировка массивов 5) Меняем местами a[1] и a[10]:[1, 9, 8, 7, 3, 6, 5) Меняем местами a[1] и a[10]:[1, 9, 8, 7, 3, 6, 5, 4, 2], 10, 11, 12;6)](/img/thumbs/92c3d6bfecd3f84d2eed8f27b2288ad4-800x.jpg)
![Сортировка массивов 5) Меняем местами a[1] и a[10]:[1, 9, 8, 7, 3, 6, 5) Меняем местами a[1] и a[10]:[1, 9, 8, 7, 3, 6, 5, 4, 2], 10, 11, 12;6)](/img/thumbs/233149b3178b435daa4f0c6708acb3d7-800x.jpg)
![Сортировка массивов 9) Меняем местами a[1] и a[8]:[1, 7, 6, 4, 3, 2, 9) Меняем местами a[1] и a[8]:[1, 7, 6, 4, 3, 2, 5], 8, 9, 10, 11, 12;10)](/img/thumbs/da64afd14e3e1a9a43a0d57618acd7c2-800x.jpg)
![Сортировка массивов 13) Меняем местами a[1] и a[6]:[2, 4, 5, 1, 3], 6, 13) Меняем местами a[1] и a[6]:[2, 4, 5, 1, 3], 6, 7, 8, 9, 10, 11, 12;14)](/img/thumbs/e606a6a610edd52c0d464a699debc088-800x.jpg)
![Сортировка массивов 19) Меняем местами a[1] и a[3]:[2, 1], 3, 4, 5, 6, 19) Меняем местами a[1] и a[3]:[2, 1], 3, 4, 5, 6, 7, 8, 9, 10, 11, 12;20)](/img/thumbs/a2e3c62fe692a8de6f64af1bc8f36794-800x.jpg)



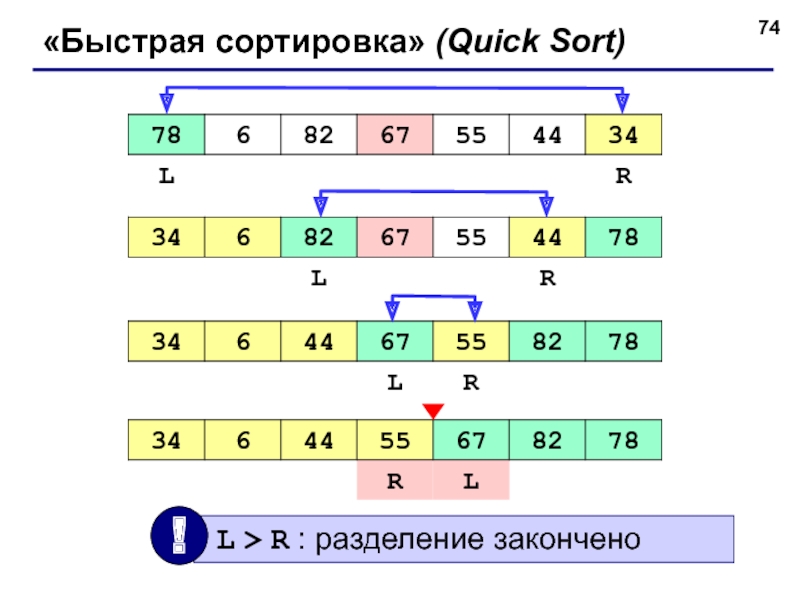

![Сортировка массивов «Быстрая сортировка» (Quick Sort)program qq;const N = 10;var A: array[1..N] of «Быстрая сортировка» (Quick Sort)program qq;const N = 10;var A: array[1..N] of integer;begin { заполнить массив } {](/img/thumbs/0f13750e9b98b616aea33462dee613c3-800x.jpg)



![Сортировка массивов Линейный поискnX := 0;for i:=1 to N do if A[i] = Линейный поискnX := 0;for i:=1 to N do if A[i] = X then begin nX :=](/img/thumbs/5a5341a07ed096b8b93a5ce38687570c-800x.jpg)
![Сортировка массивов Двоичный поискX = 7X < 884X > 46X > 6Выбрать средний Двоичный поискX = 7X < 884X > 46X > 6Выбрать средний элемент A[c] и сравнить с X.Если](/img/thumbs/71ff80e19f4cb3c23f53b3dea9edd74e-800x.jpg)
![Сортировка массивов Двоичный поиск nX := 0; L := 1; R := N; Двоичный поиск nX := 0; L := 1; R := N; {границы: ищем от A[1] до A[N]](/img/thumbs/11f5da566690c9869973fdfab64108a9-800x.jpg)




















