Сортировка-Пузырёк Выборочная QuickSort

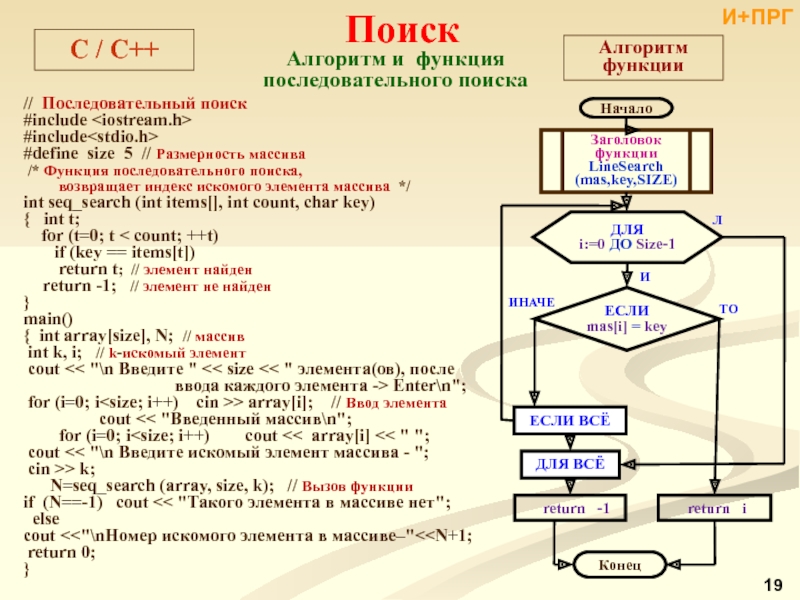
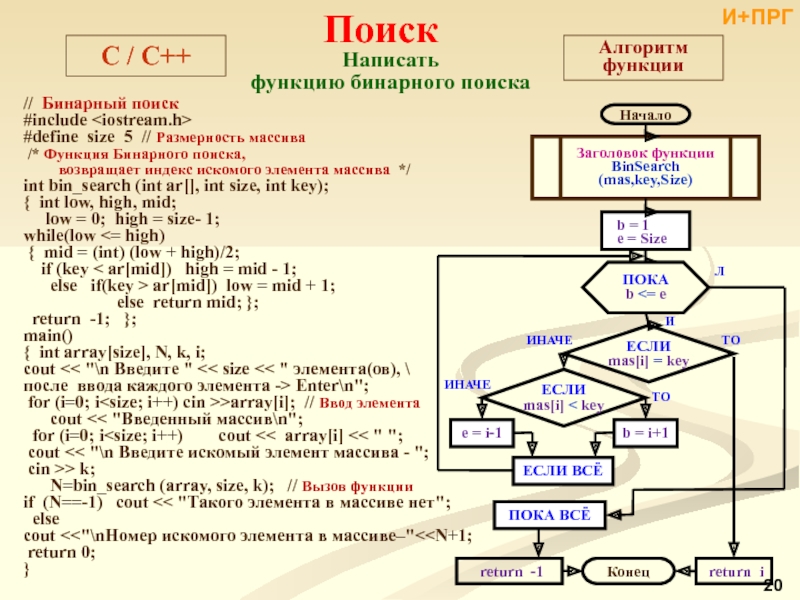
и поиска.
Данные задачи применяются как сами по себе, так

и входят как подзадачи в состав более сложных задач.
Например, дан массив N элементов, из которого надо удалить все дублирующиеся элементы. Решение сравнения каждого элемента с остальными потребует T(N2) времени. Однако если предварительно отсортировать массив (на что, как увидим позже, требуется T(N*log2(N)) времени), то найти все дубли можно за T(N) времени, сравнивая только соседние элементы, так что общее время решения задачи ‒ T(N*log2(N)).
Здесь задача сортировки вошла в другую задачу в качестве подзадачи.

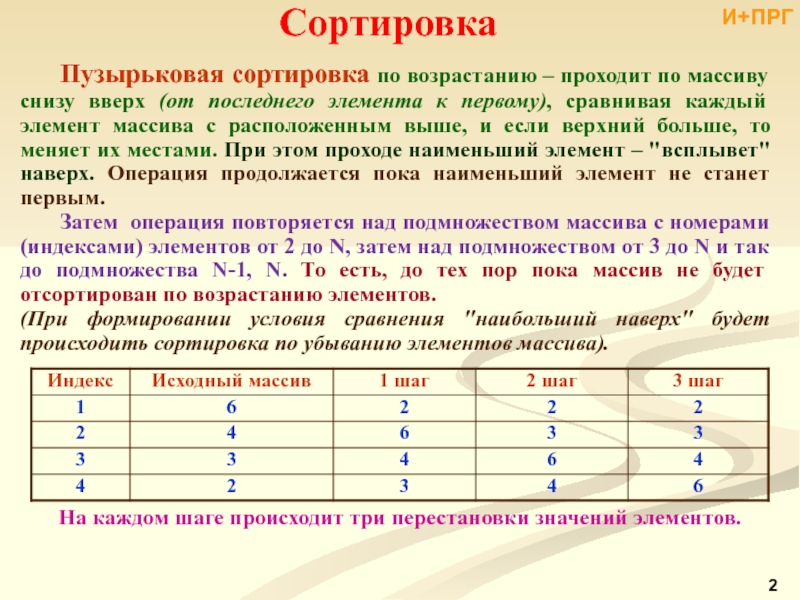
Задача сортировки формулируется следующим образом:
На вход алгоритма подается последовательность из n элементов а1,а2,...,аn; на выходе требуется получить некоторую перестановку входной последовательности a'1,a'2,...,а'n такую, что a'1≤a'2≤…≤а'n .

Алгоритмы сортировки можно разделить на алгоритмы внутренней сортировки для сортировки данных, хранящихся во внутренней оперативной памяти компьютера, и внешней сортировки – для сортировки больших объемов данных, хранящихся в файлах внешней (например, дисковой) памяти. В данном учебном курсе будут рассматриваться только алгоритмы внутренней сортировки.

И+ПРГ

(от последнего элемента к первому), сравнивая каждый элемент массива с

расположенным выше, и если верхний больше, то меняет их местами. При этом проходе наименьший элемент – "всплывет" наверх. Операция продолжается пока наименьший элемент не станет первым.
Затем операция повторяется над подмножеством массива с номерами (индексами) элементов от 2 до N, затем над подмножеством от 3 до N и так до подмножества N-1, N. То есть, до тех пор пока массив не будет отсортирован по возрастанию элементов.
(При формировании условия сравнения "наибольший наверх" будет происходить сортировка по убыванию элементов массива).

На каждом шаге происходит три перестановки значений элементов.

Сортировка

И+ПРГ

возрастанию
#include
#include
#define sz 5 // размерность массива
void main

()
{ int a[sz]; /*массив целых чисел*/
int i; //счетчик циклов сортировки
int buf; // буфер, исп. при обмене элементов массива
int k; // текущий индекс элемента массива
printf ("\nВведите в одной строке %i", sz);
printf (" целых чисел и нажмите Enter\n");
printf ("-> ");
for (k = 0; k < sz; k++) scanf ("%i", &a[k]);
// Сортировка
for (i = 0; i < sz-1; i++)
{
for (k = sz-1; k > i; k--)
{
if (a[k-1] > a[k])
{
// Меняем местами k-тый и k-1 элементы
buf = a[k-1]; a[k-1] = a[k]; a[k] = buf;
}
}
}
// Цикл сортировки закончен
// Вывод отсортированного массива
printf ("Отсортированный массив\n");
for (k = 0; k}

Сортировка

И+ПРГ

Пузырьковая сортировка

выборочной сортировки устраняет этот недостаток, здесь элемент сразу занимает свою

конечную позицию.

Выборочная сортировка – происходит следующим образом:
1. Просматривается весь первичный массив, определяется наименьший (наибольший) элемент массива и затем осуществляется единственный обмен в текущем массиве.
2. Потом просматривается массив-подмножество без наименьшего (наибольшего) элемента, определяется наименьший (наибольший) элемент подмножества и снова осуществляется единственный обмен в текущем подмножестве массива.
3. Шаг 2 повторяется пока весь массив не будет отсортирован.

Сортировка

И+ПРГ

sz 5 // размерность массива
void main ()
{ int a[sz];

// массив целых чисел
int i; // № элем., от которого ведется поиск мин. элем.
int min; // № мин. элем. в части мас. от i до конца мас.
int j; // № элемента сравниваемого с мин.
int buf; // буфер, исп. при обмене элементов массива
int k; // индекс для ввода и вывода
printf ("\nВведите в одной строке %i", sz);
printf (" целых чисел и нажмите Enter\n");

for (k=0; k // Сортировка
for (i = 0; i < sz-1; i++)
{ // Поиск мин. элем. в части мас. от a[i] до a[sz]
min = i; for (j = i+1; j < sz; j++)
if (a[j] < a[min]) min = j;
// Меняем местами a[min] и a[i]
buf = a[i]; a[i] = a[min]; a[min] = buf;
}
// Цикл сортировки закончен
// Вывод отсортированного массива
printf ("Отсортированный массив\n");
for (k = 0; k}

Сортировка

И+ПРГ

Выборочная сортировка

сравнительно неэффективны.
Среднее время работы этих алгоритмов пропорционально N2
Существуют более

быстрые методы сортировки: быстрая сортировка (Quicksort) и сортировка слиянием (метод Шелла).
Среднее время работы этих методов пропорционально N*log2(N)


Зависимость времени сортировки от количества элементов массива (N) и
мощности алгоритма

Сортировка

И+ПРГ

Метод сортировки разделением:
Из массива выбирается опорный элемент P.
Сравнивая

элементы массива с P и разделяем (сортируем) массив на 2-а подмассива (подмножества). Слева от P элементы меньшие и равные P, а справа – большие или равные.
Для обоих подмножеств, если в них больше 1-го элемента, проделывается та же процедура.
Процесс повторяются для каждой части массива пока он не будет отсортирован.

Опорный элемент выбирается или случайным образом, или как среднее некоторого количества значений массива (например, первого и последнего).

Сортировка

И+ПРГ

Устанавливаем начальные значения индексов I=1 и J=N.
Выбираем опорный

элемент P = M[K], где K = (I +J) / 2.
Сравниваем M[I] <= P, если ДА, то увеличиваем I (I=I+1).
Затем сравниваем M[J] >= P, если ДА, то уменьшаем J (J=J-1).
Если НЕТ и I<=J, то меняем местами M[I] и M[J].
Повторяем шаги 4-6 пока I<=J.
В результате массив разделяется на 2-е части, слева от P элементы меньше или равны P, а справа – больше или равны.
Над каждой частью (подмножеством) массива повторяем шаги 2-7. Получаем 4-е подмножества.
Над каждым подмножеством повторяем шаги 2-7. Выполняем эти операции пока массив не будет отсортирован.

Быстрая сортировка (разделением):

Алгоритм быстрой сортировки

Сортировка

И+ПРГ

Уст. нач. знач. I=1 и J=N.
3. Выб. Опор.элем.

P = M[(M[1]+M[N])/2].
4. Сравн. M[I] <= P, если ДА, то I=I+1.
5. Сравн. M[J] >= P, если ДА, то J=J-1.
6. Если НЕТ и I<=J, то меняем местами M[I] и M[J].
7. Повторяем шаги 2-6 пока I<=J.
8. Массив раздел. на 2-е части, слева от P элементы <= P, а справа >= P.
9. Над кажд. подмнож. мас. повт. шаги 2-7. Получ. 4 подмнож.
10. Над кажд. подмнож. повт. шаги 2-7. Вып. эти операции пока массив не будет отсортирован.

Пример:
1-2. {5 2 7 2 13 3 8 15 19}
3. P=13
4-7. {5 2 7 2 13 3 8 15 19} - меняем местами 13 и 8 =
{5 2 7 2 8 3 13 15 19}
8. Массив разделен на две части по 13.
9-10. Сортируем подмножество
{5 2 7 2 8 3 13 15 19}
2-7. P=7 -> {5 2 7 2 8 3 13 15 19} =
{5 2 3 2 8 7 13 15 19} –
P=2 -> {5 2 3 2 8 7 13 15 19} =
{2 2 3 5 8 7 13 15 19} –
P=8 -> {2 2 3 5 8 7 13 15 19} =
{2 2 3 5 7 8 13 15 19}

Нарисовать алгоритм быстрой сортировки.

Алгоритм быстрой сортировки

Сортировка

И+ПРГ

– прямой смысл реализовать эту сортировку в виде рекурсивной функции
Сортировка
И+ПРГ

на С.
Сортировка
И+ПРГ

{ long i, j; int p, temp;
// Инициализация нижней

границы
i = Low;
// Инициализация верхней границы
j = High;
// опорный элемент
p = array[(int) (Low+High)/2];
do { while (array[i] < p) i++;
while (array[j] > p) j--;
if (i<=j) // Если верно, то обмен
{ temp = array[i]; array[i] = array[j];
array[j] = temp; i++; j--; } }
while (i<=j); // пока индексы не пересекутся

if (j > Low) quicksort (j, Low);
/* Если подмассив [j, Low] более одного элемента, он сортируется функцией quicksort */
if (High > i) quicksort (High, i);
// Аналогично для [High, i]
}

C / C++

Сортировка

И+ПРГ

Быстрая сортировка

C / C++

#include
#include
int array[10000]; // Объявление массива
/* Функция - Быстрая сортировка
………………………………………… */
main() // Главная функция
{ int i; int size; // количества элементов
cout << "\n Введите количество элементов сортируемого массива size = ";
cin >> size;
for (i=0; i> array[i];
// Чтение очередного элемента массива
for (i=0; i cout << array[i] << " ";
quicksort (size-1, 0);
// Вывод отсортированного массива
cout << "\n
Отсортированный массив\n ";
for (i=0; i cout << array[i] << " ";
return 0;
}

массива, разделен-ных одинаковым расстоянием, таким образом, чтобы элементы были упорядочены

по расстоянию. Затем это расстояние делится пополам и процесс повторяется.

Алгоритм сортировки Шелла:

В этом методе первоначально рассматриваются элементы отстоящие друг от друга на расстояние d=[n/2], где [ ] - операция взятия целой части, и n - количество элементов исходного массива.
На следующих шагах d меняется по закону d=[d/2], при d=1 метод Шелла вырождается в метод стандартного обмена ("Метод Пузырка")

Сортировка

И+ПРГ

6 и 8 ->
{6,2,4,8,3,9} - сравниваем 3 и 2, переставляем

->
{6,3,4,8,2,9} - сравниваем 4 и 9 ->
далее d=[d/2]=[3/2]=1.
И алгоритм выродился в метод "Пузырька"

В этом примере не очень видна эффективность метода, но представьте, что вы сортируете 1000 элементов. Этот метод обеспечивает более быстрое перебрасывание больших элементов вправо и меньших влево, чем метод "Пузырька" и этим обеспечивает большее быстродействие.

Сортировка методом Шелла

Сортировка

И+ПРГ

элементов }
n:integer;
procedure sort_shell (var a:array of integer);
Var

bis,i,j,k:longint; h:word;
begin
bis:=high(a); k:=bis shr 1;
While k>0 do
Begin
For i:=0 To bis-k do
begin
j:=i;
While (j>=0) And (a[j]>a[j+k]) do
begin
h:=a[j]; a[j]:=a[j+k]; a[j+k]:=h; dec(j,k);
end;
end;
k:=k shr 1;
End;
End;

begin
writeln('введите 10 элементов массива:');
for n:=1 to 10 do readln(a[n]);
sort_shell(a);
writeln('после сортировки:');
for n:=1 to 10 do write(a[n],' ');
end.

Сортировка методом Шелла

Сортировка

И+ПРГ

Pascal

важнейших задач обработки данных.
Для решения задачи поиска необходимо, чтобы

данные в памяти ЭВМ были организованы определенным образом. Основные способы организа-ции данных: массивы элементов одинакового типа, структуры данных, линейные списки, деревья, произвольные графы. Алгоритмы поиска существенно зависят от способа организации данных.
Рассмотрим алгоритмы поиска в МАССИВАХ:
а) последовательный (линейный) поиск -- простейший метод поиска элемента, находящегося в неупорядоченном массиве данных, это последовательный просмотр каждого элемента массива, продолжающийся до тех пор, пока не будет найден желаемый элемент. Если просмотрен весь массив, но элемент не найден – значит он отсутствует в массиве. Для последовательного поиска в среднем требуется (N+1)/2 сравнений, а в худшем N. Линейный поиск может применяться и для упорядоченных (отсортированных) массивов, НО эффективнее использовать:
б) бинарный (двоичный, дихотомический, логарифмический) поиск – он состоит в разделении упорядоченного массива пополам, определении в какой половине находится искомый элемент, затем это половина снова разделяется пополам и так пока полученное подмножество из одного элемента не станет равным искомому. Для бинарного поиска в худшем случае требуется log2(N) сравнений.

И+ПРГ

5 // Размерность массива
/* Функция последовательного поиска,

возвращает индекс искомого элемента массива */
int seq_search (int items[], int count, char key)
{ int t;
for (t=0; t < count; ++t)
if (key == items[t])
return t; // элемент найден
return -1; // элемент не найден
}
main()
{ int array[size], N; // массив
int k, i; // k-искомый элемент
cout << "\n Введите " << size << " элемента(ов), после
ввода каждого элемента -> Enter\n";
for (i=0; i> array[i]; // Ввод элемента
cout << "Введенный массив\n";
for (i=0; i cout << "\n Введите искомый элемент массива - ";
cin >> k;
N=seq_search (array, size, k); // Вызов функции
if (N==-1) cout << "Такого элемента в массиве нет";
else
cout <<"\nНомер искомого элемента в массиве–"< return 0;
}

5 // Размерность массива
/* Функция Бинарного поиска,

возвращает индекс искомого элемента массива */
int bin_search (int ar[], int size, int key);
{ int low, high, mid;
low = 0; high = size- 1;
while(low <= high)
{ mid = (int) (low + high)/2;
if (key < ar[mid]) high = mid - 1;
else if(key > ar[mid]) low = mid + 1;
else return mid; };
return -1; };
main()
{ int array[size], N, k, i;
cout << "\n Введите " << size << " элемента(ов), \
после ввода каждого элемента -> Enter\n";
for (i=0; i>array[i]; // Ввод элемента
cout << "Введенный массив\n";
for (i=0; i cout << "\n Введите искомый элемент массива - ";
cin >> k;
N=bin_search (array, size, k); // Вызов функции
if (N==-1) cout << "Такого элемента в массиве нет";
else
cout <<"\nНомер искомого элемента в массиве–"< return 0;
}