Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СТАТИКА
Содержание
- 1. СТАТИКА
- 2. Основные понятия
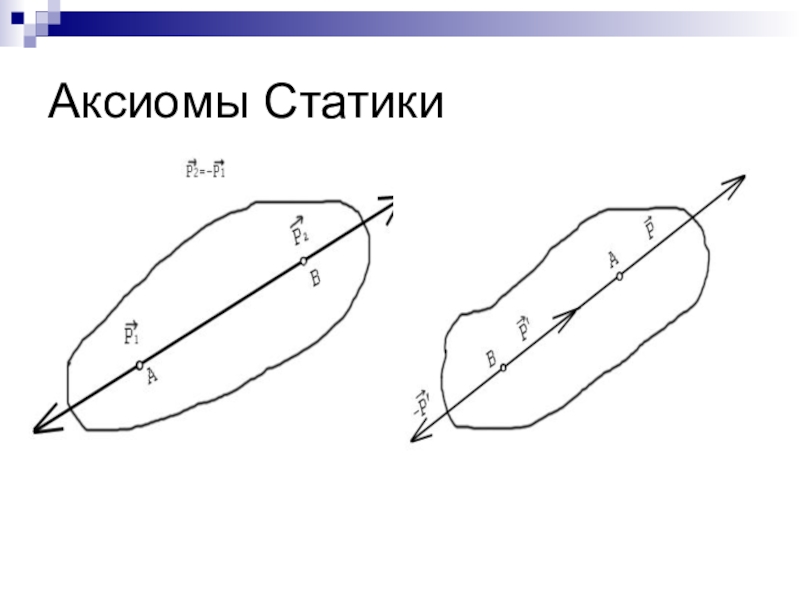
- 3. Аксиомы Статики
- 4. Слайд 4
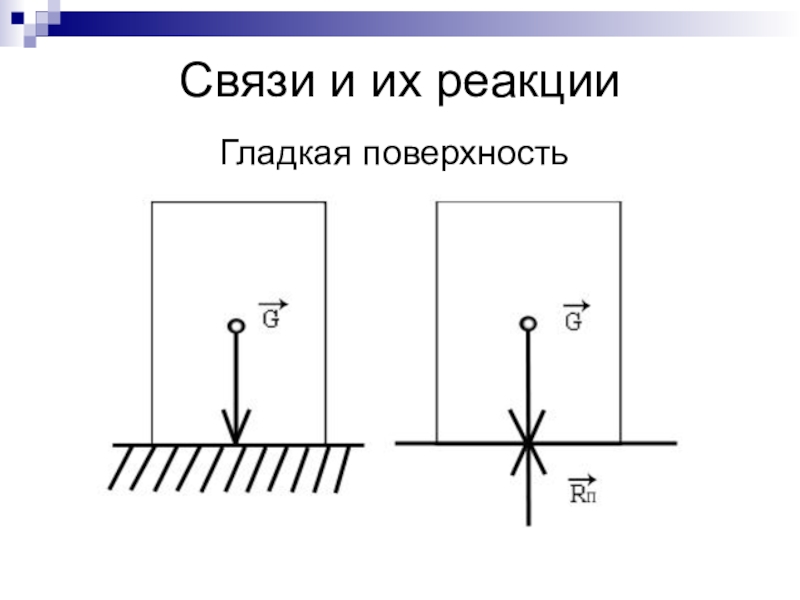
- 5. Связи и их реакцииГладкая поверхность
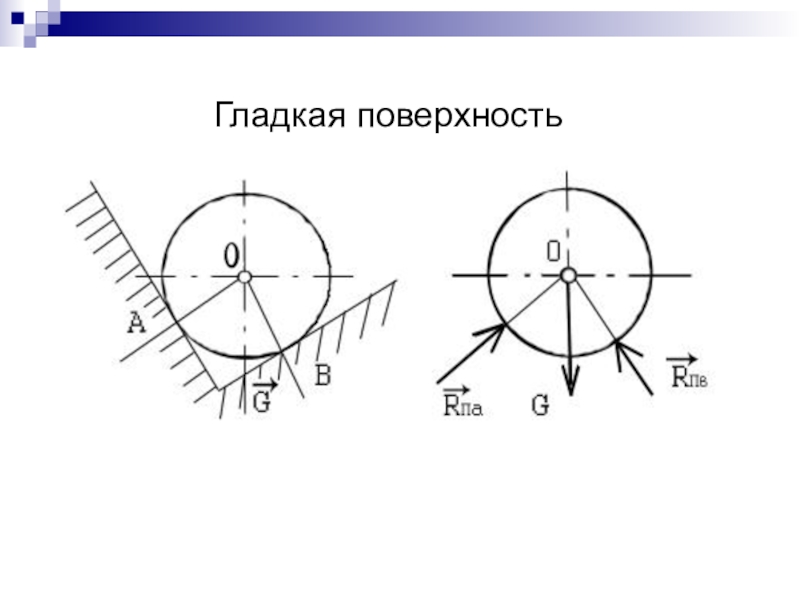
- 6. Гладкая поверхность
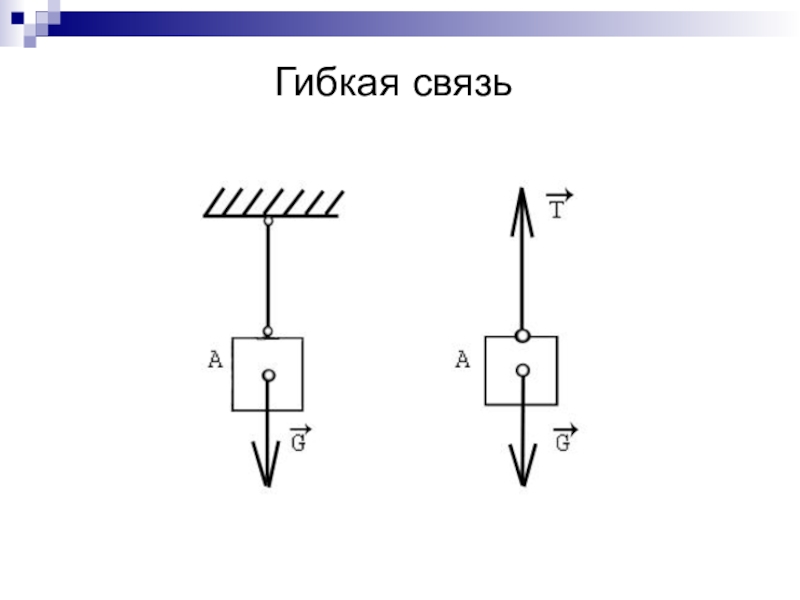
- 7. Гибкая связь
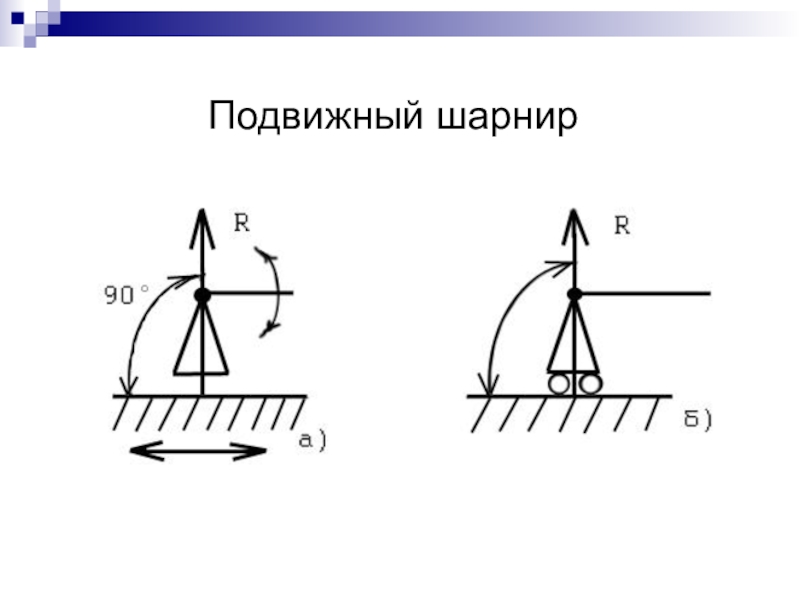
- 8. Подвижный шарнир
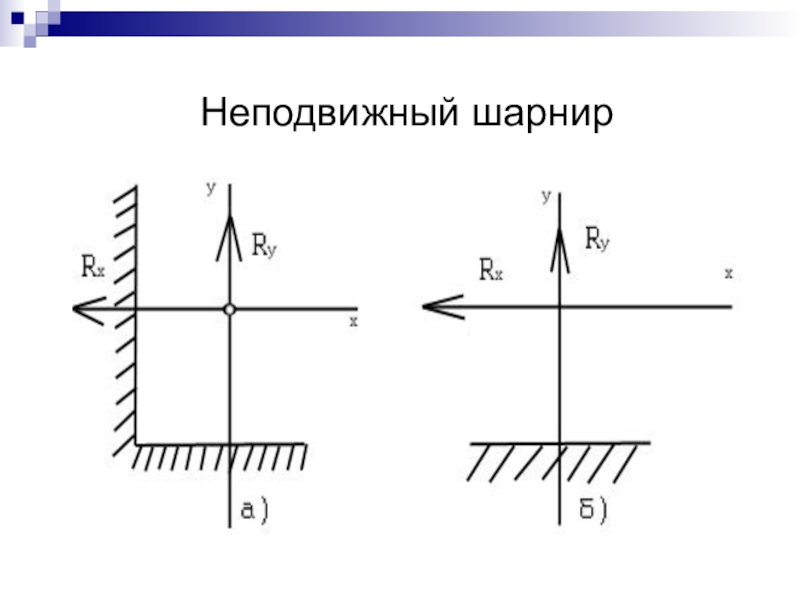
- 9. Неподвижный шарнир
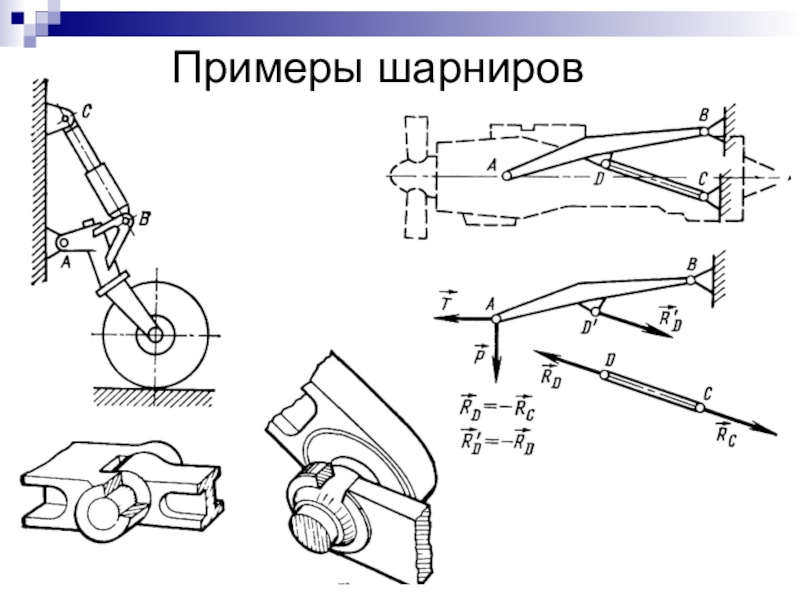
- 10. Примеры шарниров
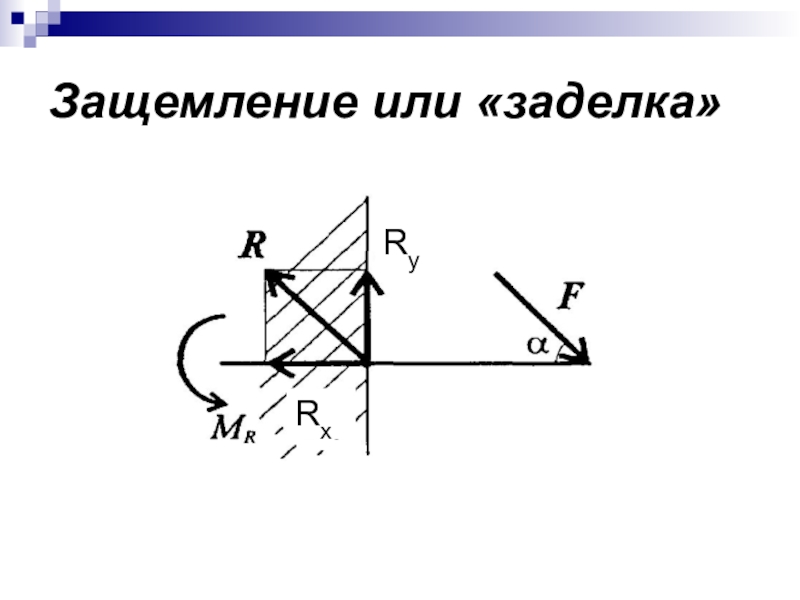
- 11. Защемление или «заделка» RyRx
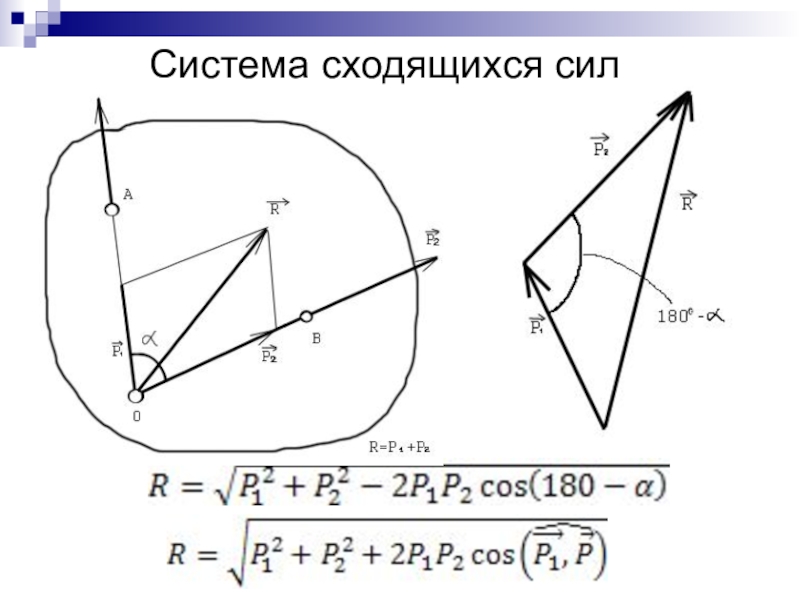
- 12. Система сходящихся сил
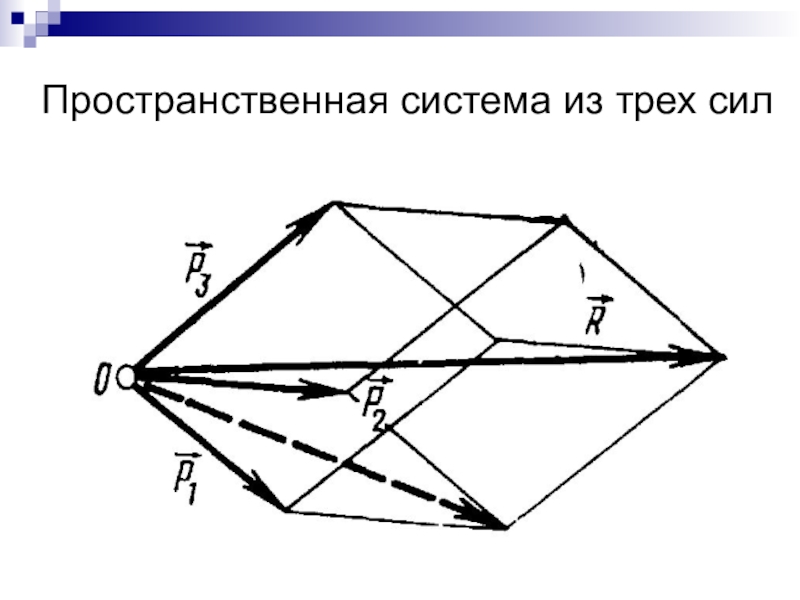
- 13. Пространственная система из трех сил
- 14. Слайд 14
- 15. Равновесие системы сходящихся сил
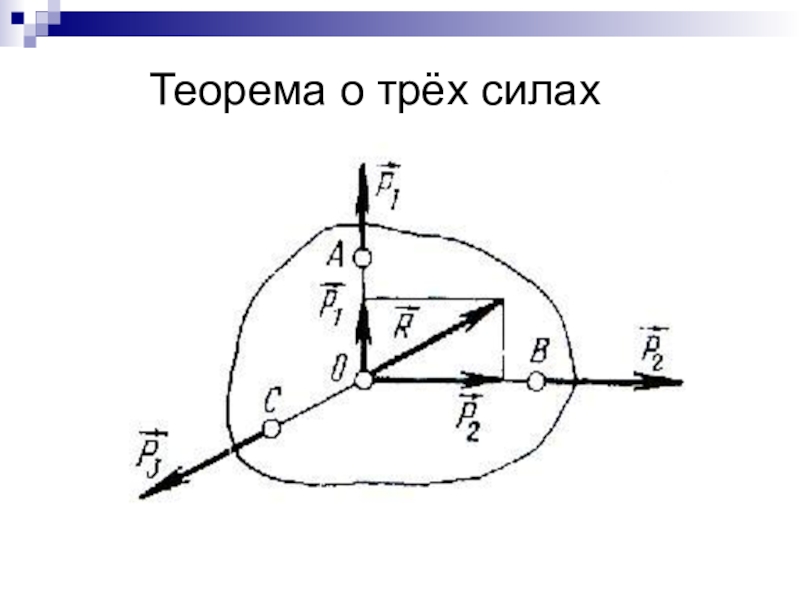
- 16. Теорема о трёх силах
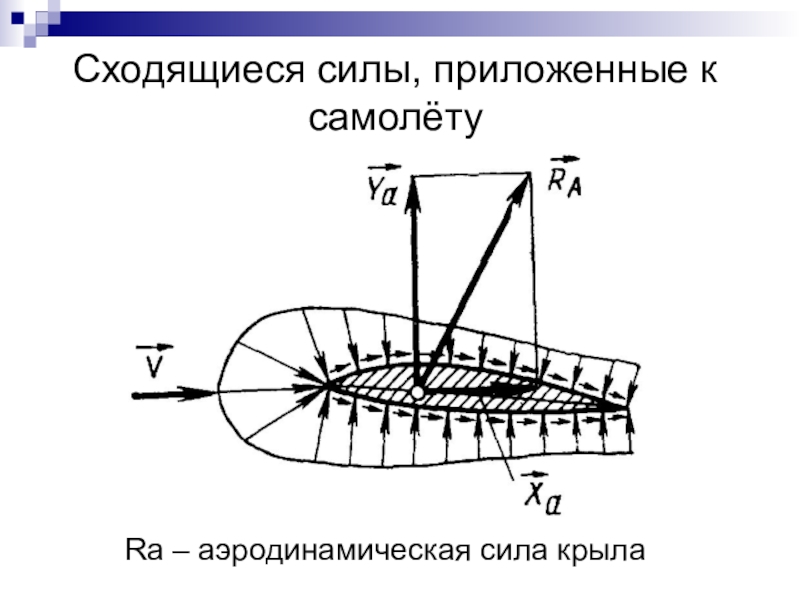
- 17. Сходящиеся силы, приложенные к самолётуRa – аэродинамическая сила крыла
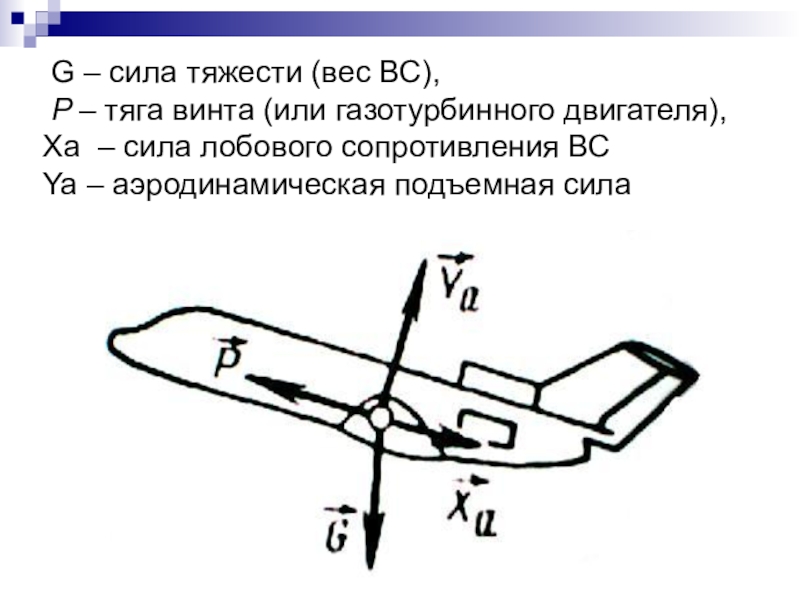
- 18. G – сила тяжести (вес ВС),
- 19. Теорема Вариньона о моменте равнодействующей сходящейся системы сил
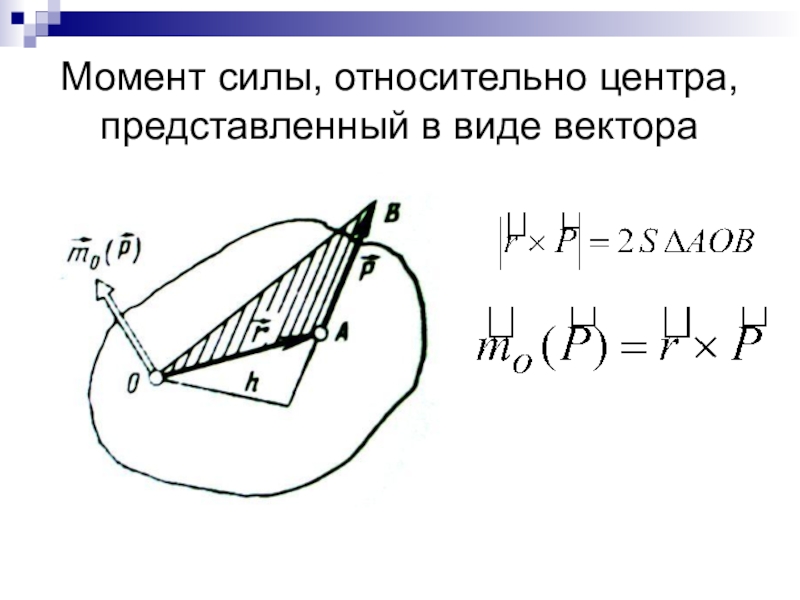
- 20. Момент силы, относительно центра, представленный в виде вектора
- 21. Слайд 21
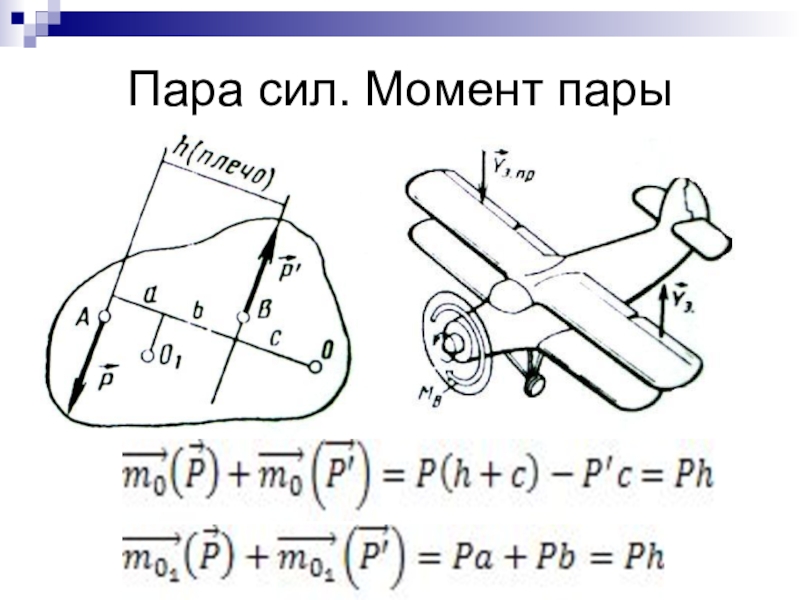
- 22. Пара сил. Момент пары
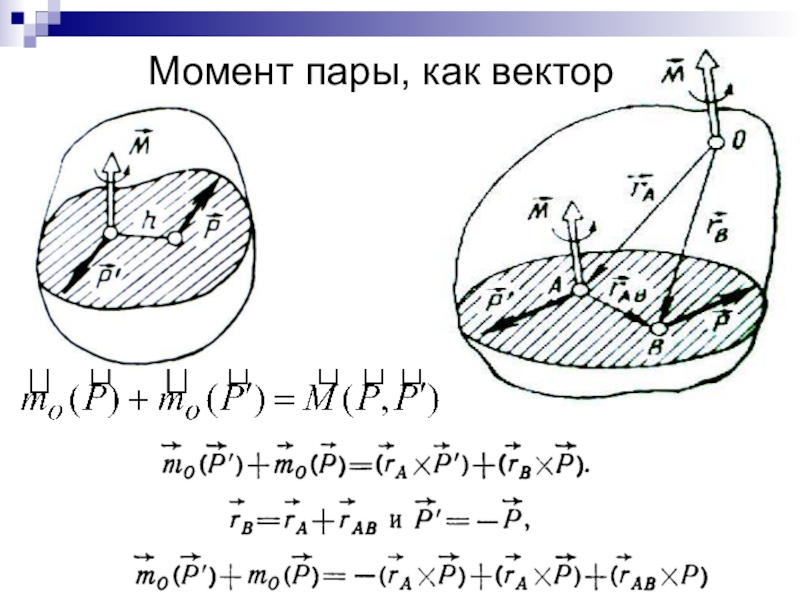
- 23. Момент пары, как вектор
- 24. Сложение пар. Равновесие тела под действием системы пар
- 25. ЭКВИВАЛЕНТНОСТЬ ПАРДействие пары на тело не изменится,
- 26. Слайд 26
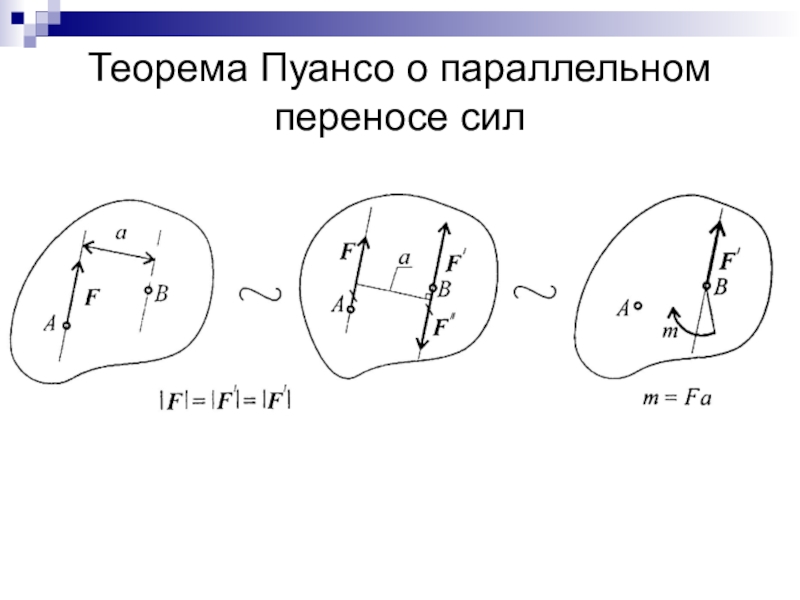
- 27. Теорема Пуансо о параллельном переносе сил
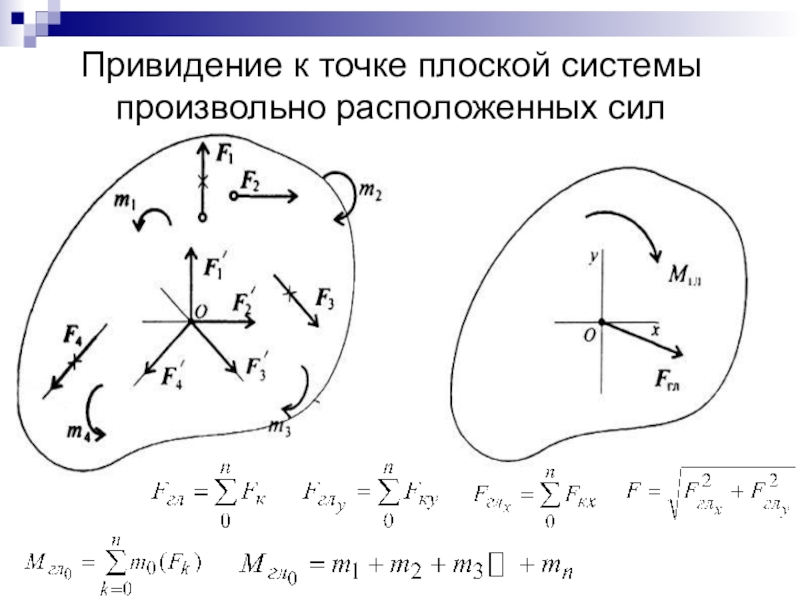
- 28. Привидение к точке плоской системы произвольно расположенных сил
- 29. Точку приложения равнодействующей можно определить по формуле
- 30. Слайд 30
- 31. Основная форма уравнения равновесия:
- 32. Теорема Вариньона о моменте равнодействующей произвольной плоской системы сил
- 33. Пространственная система силMoo(F) = np. F·a,
- 34. Пространственная сходящаяся системы силFx = Fcosx; Fy
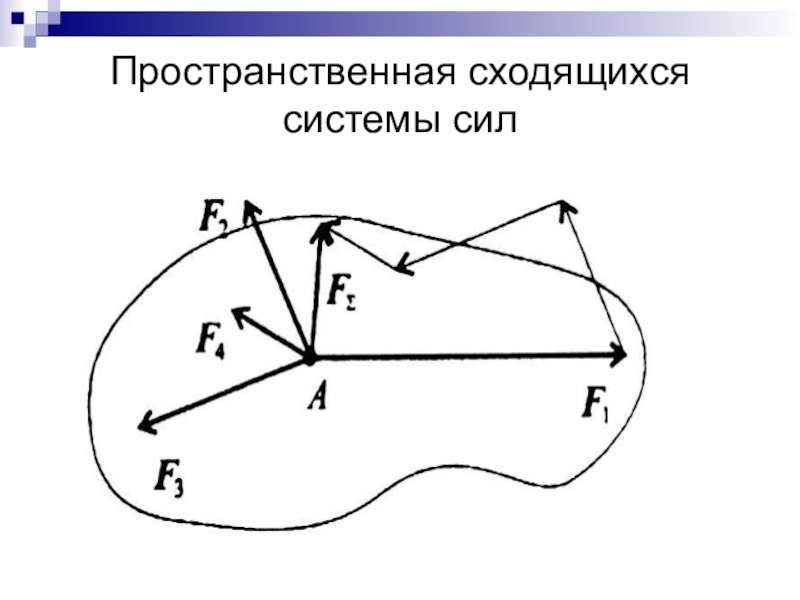
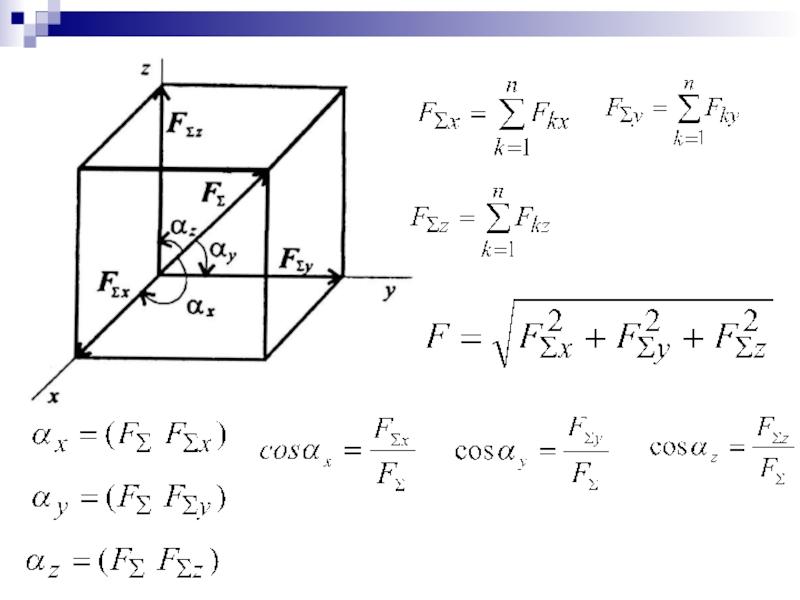
- 35. Пространственная сходящихся системы сил
- 36. .
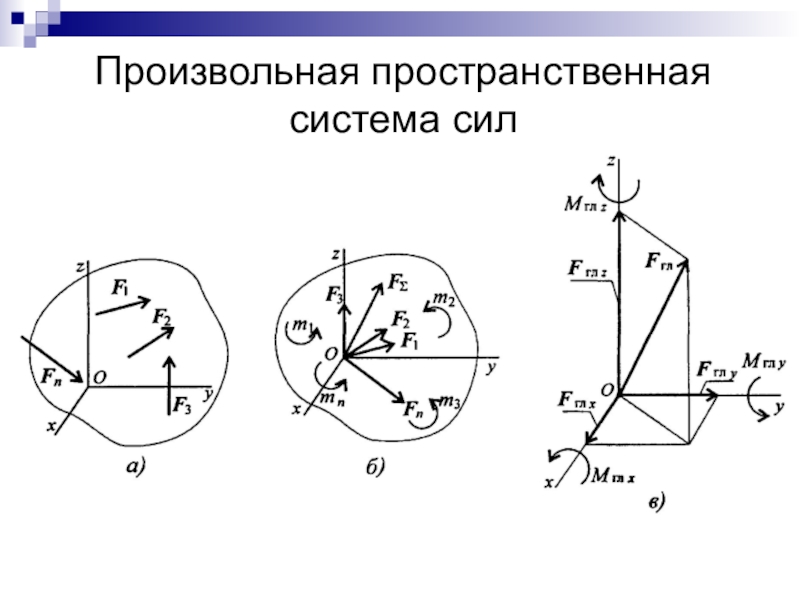
- 37. Произвольная пространственная система сил
- 38. Слайд 38
- 39. Уравнения равновесия пространственной системы сил
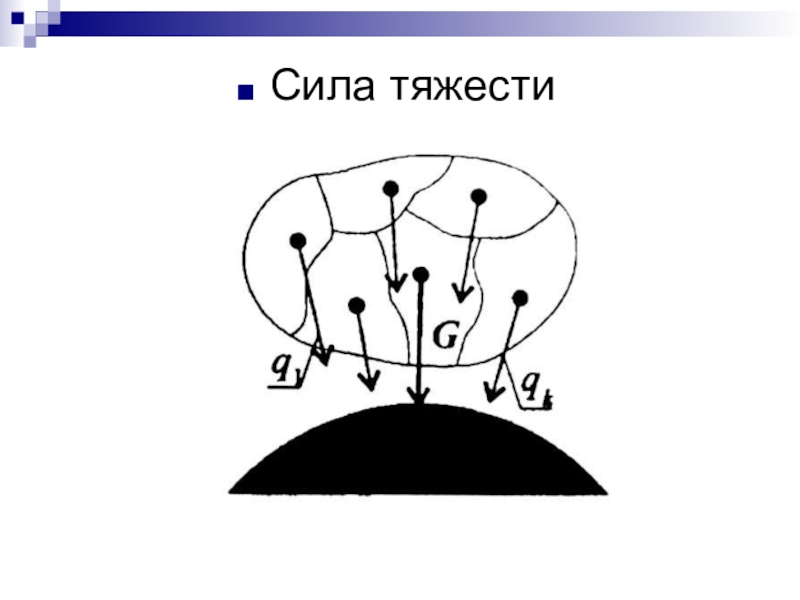
- 40. Сила тяжести
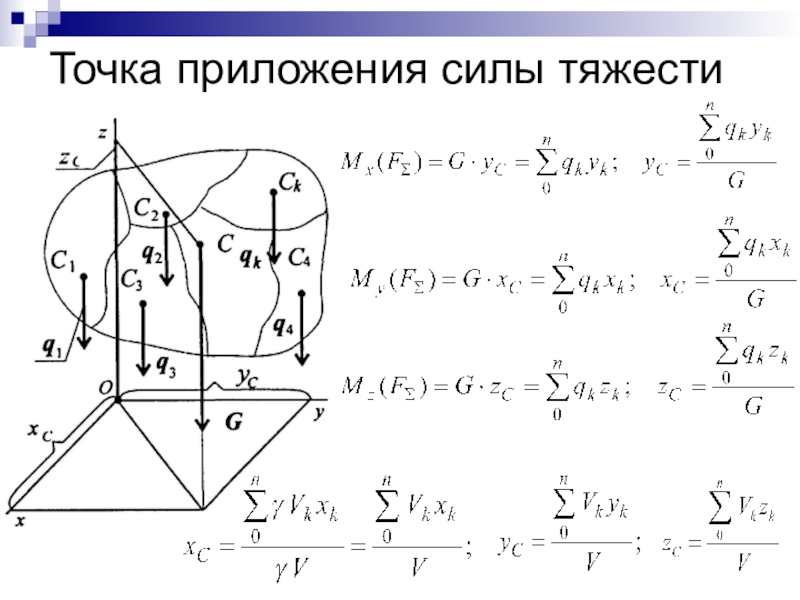
- 41. Точка приложения силы тяжести
- 42. Для плоских тел: V = Ah, где
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
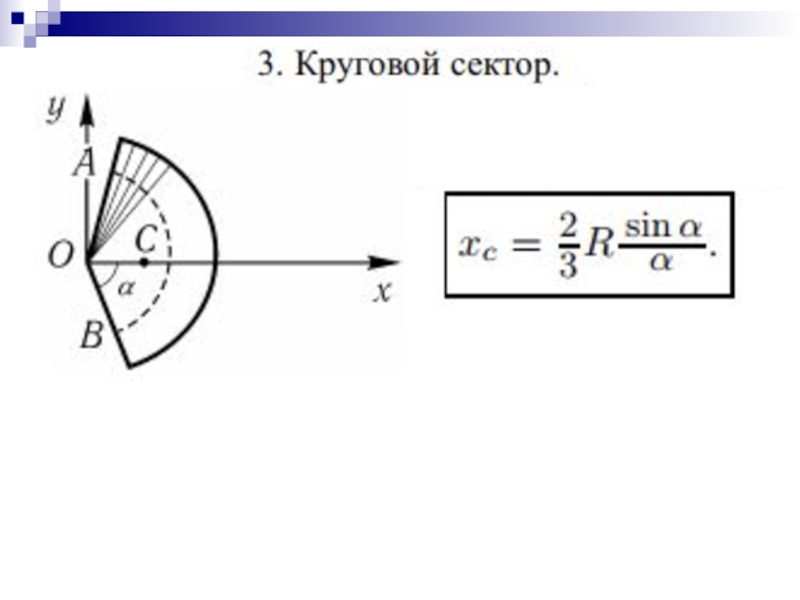
- 46. При решении задач используются следующие методы:1) Аналитический (интегрированием)
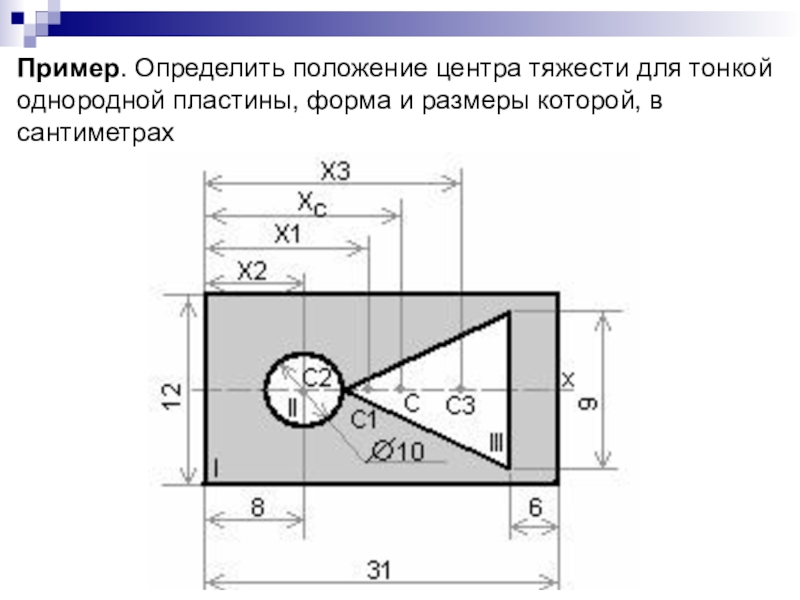
- 47. Пример. Определить положение центра тяжести для тонкой однородной пластины, форма и размеры которой, в сантиметрах
- 48. Решение.Данную фигуру представляем состоящей из трех простых
- 49. Координаты центра тяжести простых фигур: х1=31/2=15,5 см, х2=8см, х3=31-6-12/3=21см, где
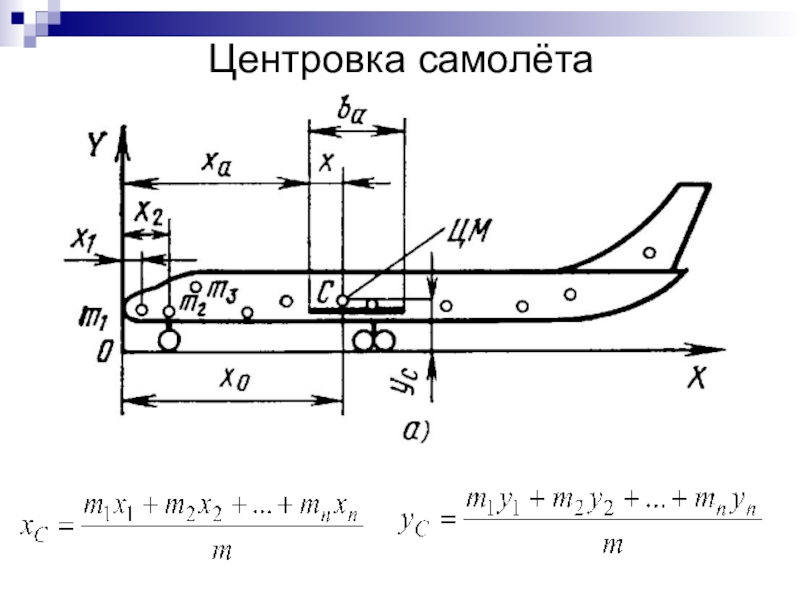
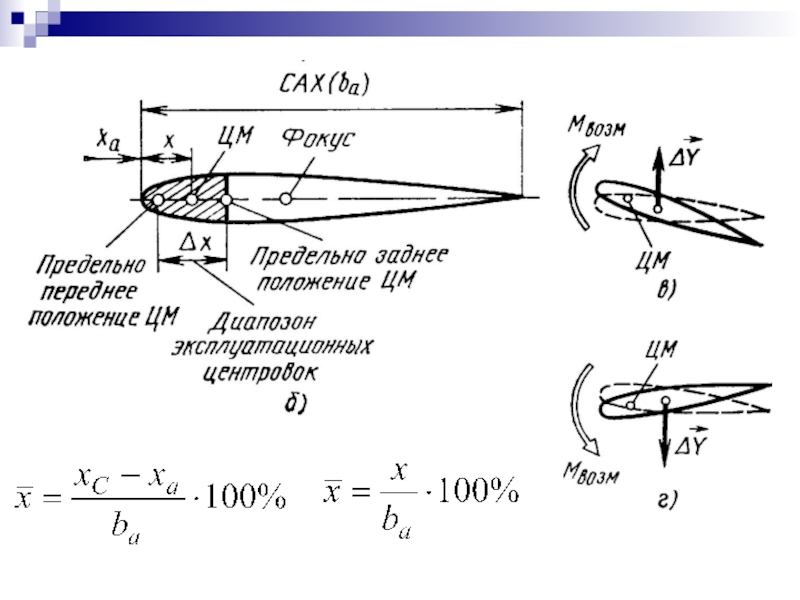
- 50. Центровка самолёта
- 51. Слайд 51
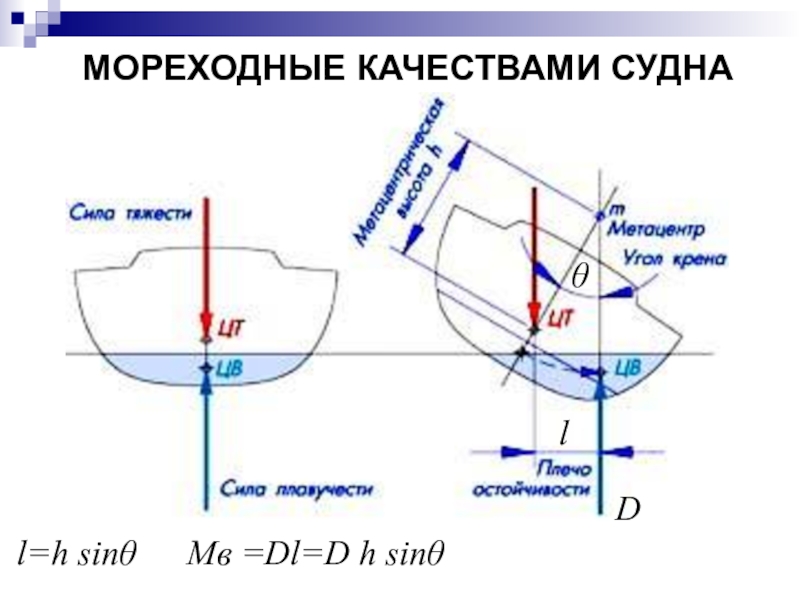
- 52. МОРЕХОДНЫЕ КАЧЕСТВАМИ СУДНАlql=h sinqMв =Dl=D h sinqD
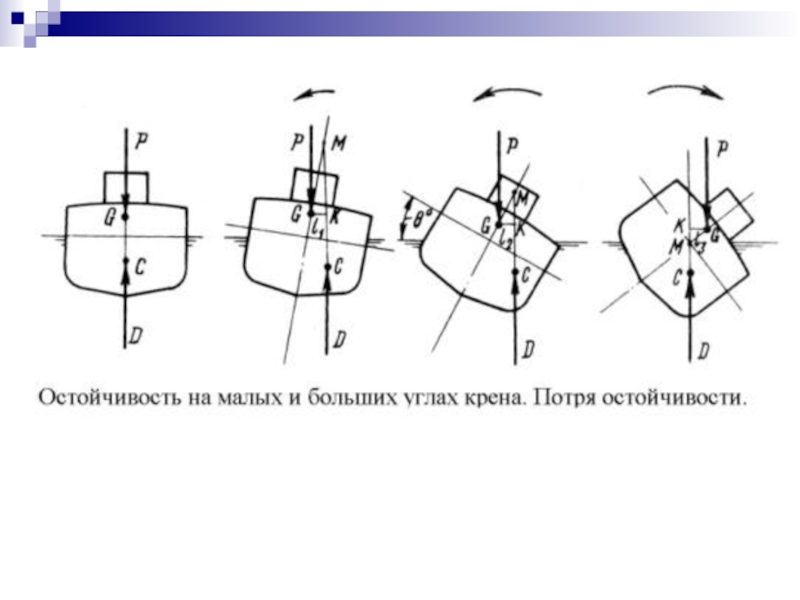
- 53. Слайд 53
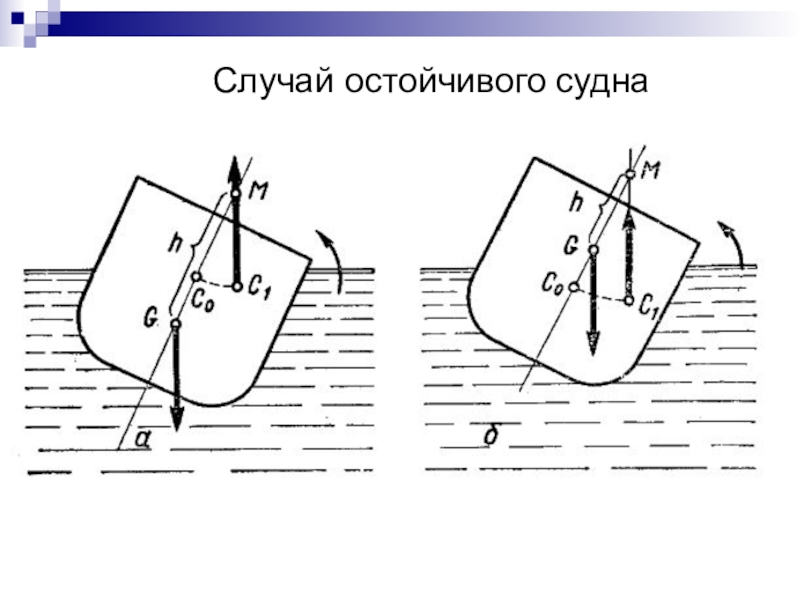
- 54. Случай остойчивого судна
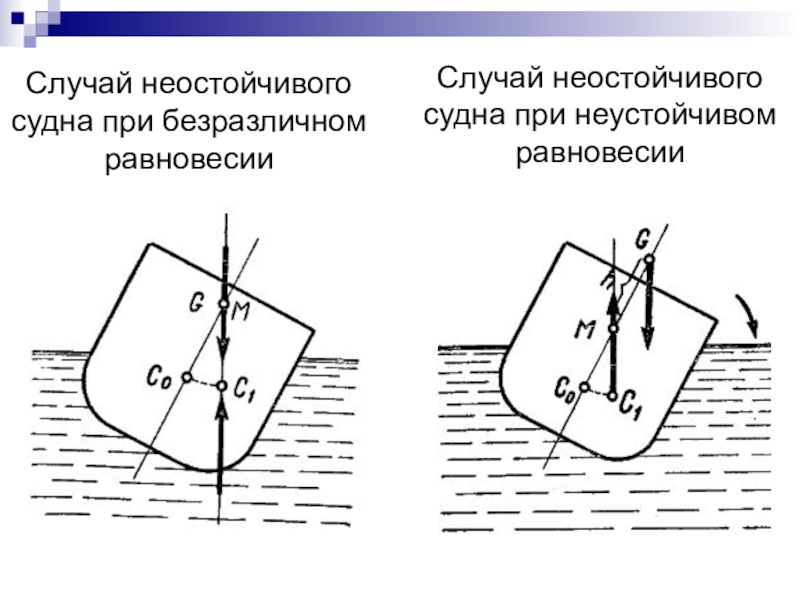
- 55. Случай неостойчивого судна при безразличном равновесииСлучай неостойчивого судна при неустойчивом равновесии
- 56. Для классической яхты “Contessa 32” потеря остойчивости наступает только при крене 155°
- 57. Понятие о трении. Виды тренияFтр = Ff
- 58. 0 < Ff < Ff 0Ff 0
- 59. .До тех пор пока линия действия равнодействующей
- 60. Nk;Трения каченияFдвr где k – максимальное
- 61. Скачать презентанцию
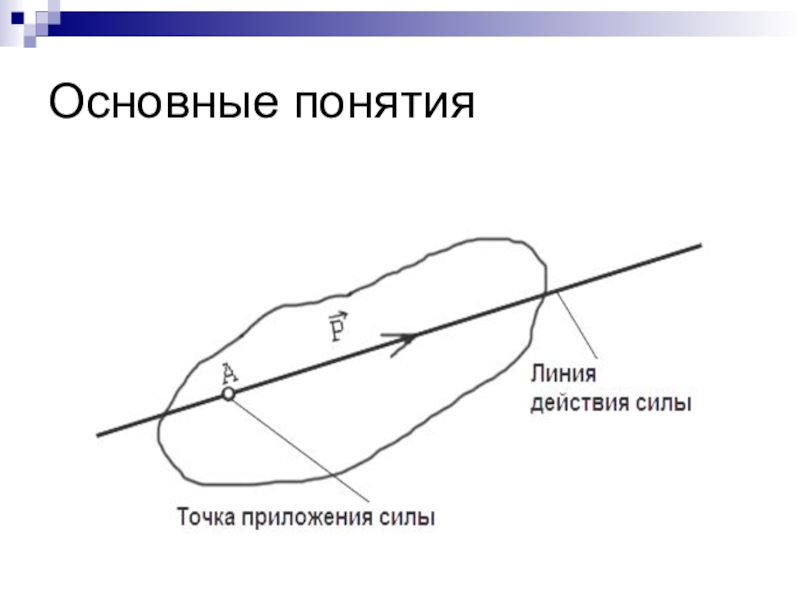
Основные понятия
Слайды и текст этой презентации
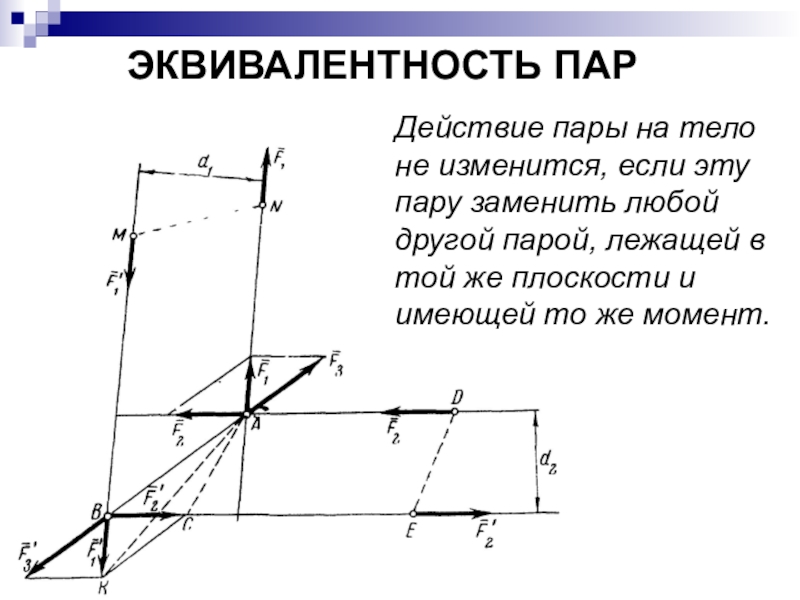
Слайд 25ЭКВИВАЛЕНТНОСТЬ ПАР
Действие пары на тело не изменится, если эту пару
заменить любой другой парой, лежащей в той же плоскости и
имеющей то же момент.
Слайд 26
Свойства пары сил:
1. Действие пары на тело не изменится,
если переместить пару в другое положение в плоскости ее действия.2. Действие пары на тело не изменится, если одновременно изменить модуль сил пары и величину ее плеча, сохраняя при этом численное значение и знак, момента пары.
Слайд 29Точку приложения равнодействующей можно определить по формуле
где d –
расстояние от выбранной точки приведения до
точки приложения равнодействующей;Мгл – величина главного момента относительно
выбранной точки приведения;
Fгл – величина главного вектора системы сил.
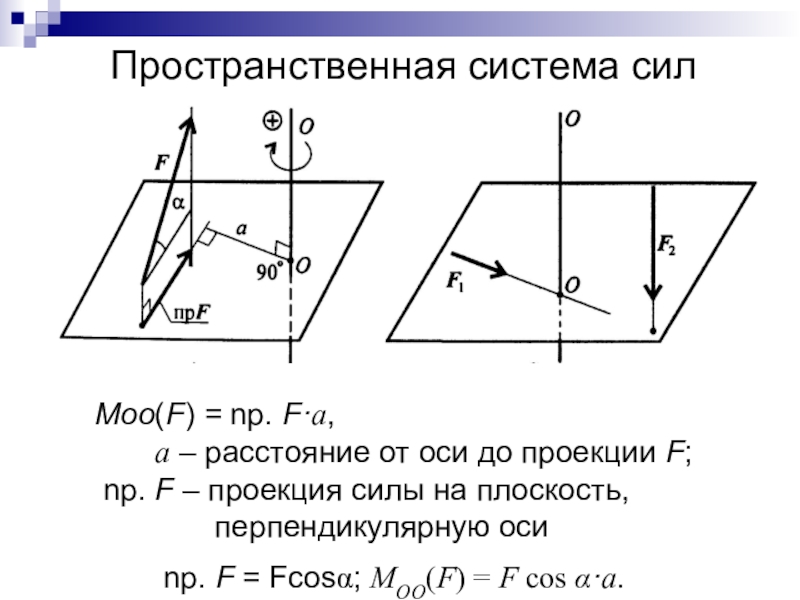
Слайд 33Пространственная система сил
Moo(F) = np. F·a,
a
– расстояние от оси до проекции F;
np. F –
проекция силы на плоскость, перпендикулярную оси
np. F = Fcos; МОО(F) = F cos ·a.
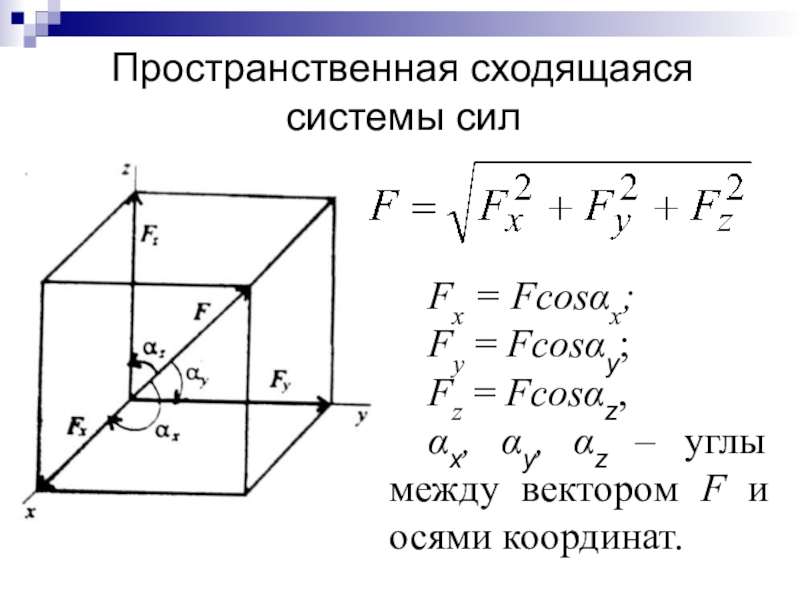
Слайд 34Пространственная сходящаяся системы сил
Fx = Fcosx;
Fy = Fcosy;
Fz
= Fcosz,
x, y, z – углы между вектором F и
осями координат.
Слайд 42Для плоских тел: V = Ah,
где А – площадь
фигуры, h – ее высота
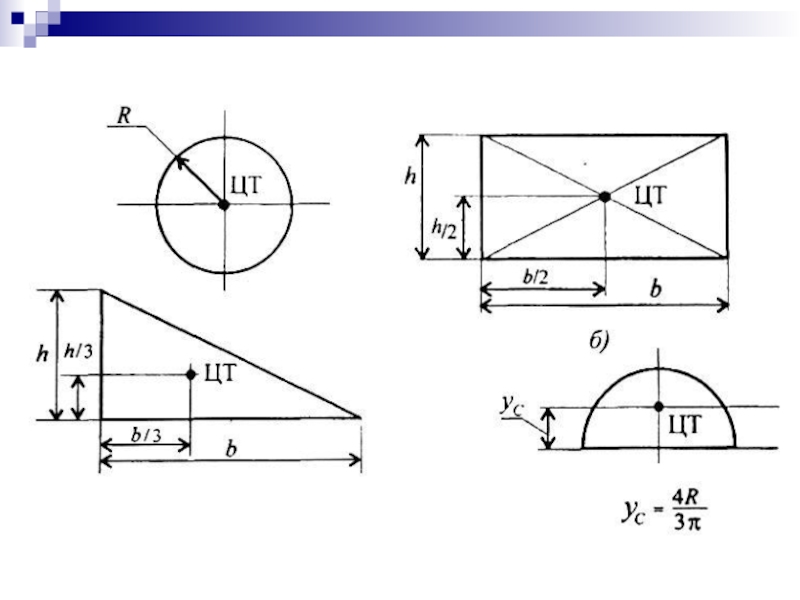
Определение координат центра тяжести плоских фигур
Координаты
центра тяжести сечения можно выразить через статический момент:
Слайд 47Пример. Определить положение центра тяжести для тонкой однородной пластины, форма
и размеры которой, в сантиметрах
Слайд 48Решение.
Данную фигуру представляем состоящей из трех простых фигур: 1 –
прямоугольник, 2 – круга, 3 – треугольника.
Площади кругового и треугольного
отверстий вводим в расчет со знаком минус, а площадь прямоугольника – без учета имеющихся в нем отверстий.Площади простых фигур:
Высота треугольника
Слайд 49Координаты центра тяжести простых фигур:
х1=31/2=15,5 см,
х2=8см,
х3=31-6-12/3=21см,
где 12/3 – расстояние
от центра тяжести треугольника до его основания, равное 1/3 высоты.
Координата
центра тяжести заданной фигуры
Слайд 55Случай неостойчивого судна при безразличном равновесии
Случай неостойчивого судна при неустойчивом
равновесии
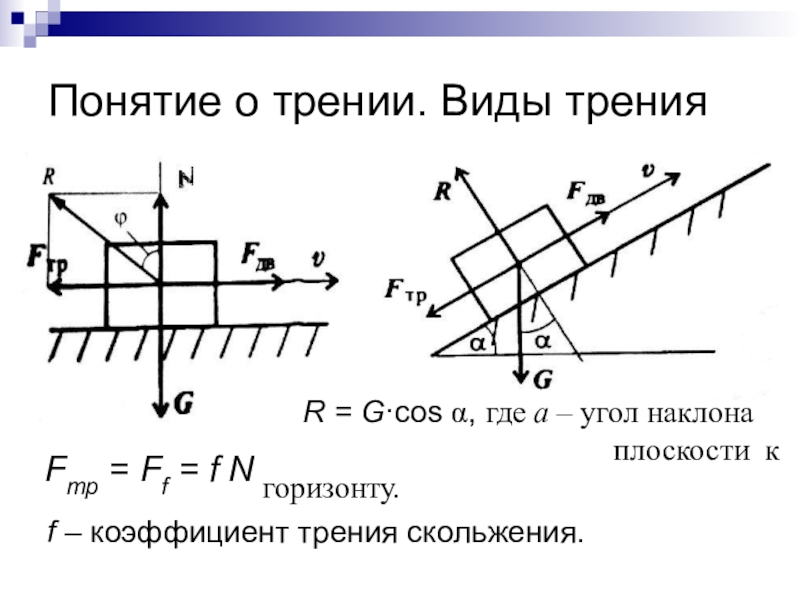
Слайд 57Понятие о трении. Виды трения
Fтр = Ff = f N,
f
– коэффициент трения скольжения.
R = G·cos , где а –
угол наклона плоскости к горизонту.
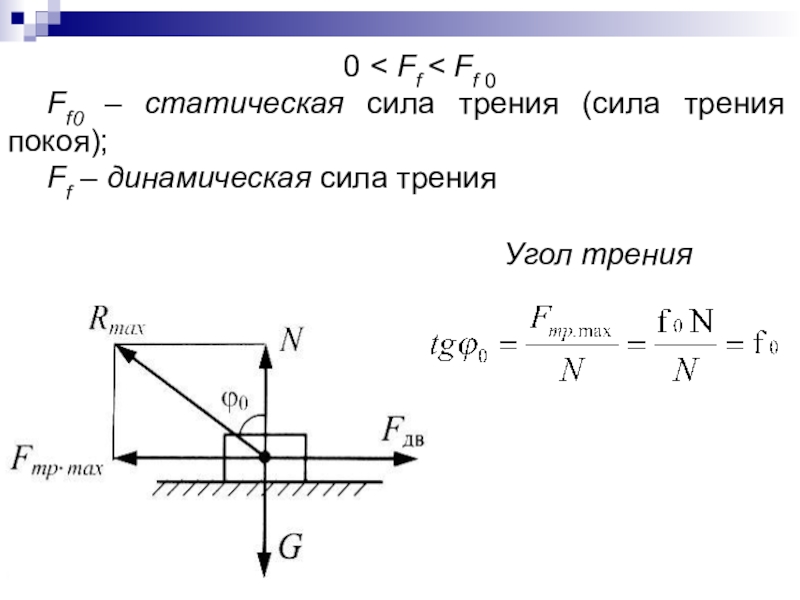
Слайд 580 < Ff < Ff 0
Ff 0 – статическая сила
трения (сила трения покоя);
Ff – динамическая сила трения
Угол трения
Слайд 59.
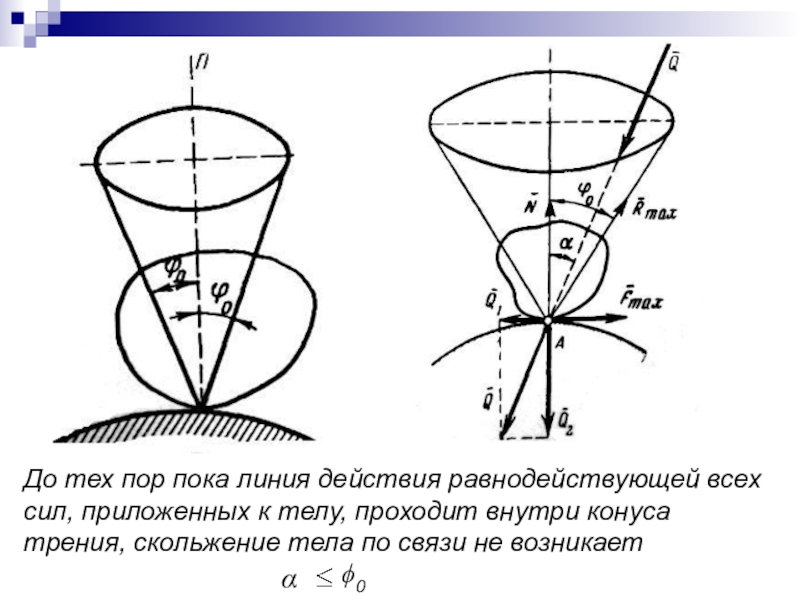
До тех пор пока линия действия равнодействующей всех сил, приложенных
к телу, проходит внутри конуса трения, скольжение тела по связи
не возникает0
Слайд 60 Nk;
Трения качения
Fдвr
где k – максимальное значение плеча (половина
колеи) принимается за коэффициент трения качения.
N = G;
Cталь по
стали – k = 0,005 см; резиновая шина по шоссе – k = 0,24 см.
