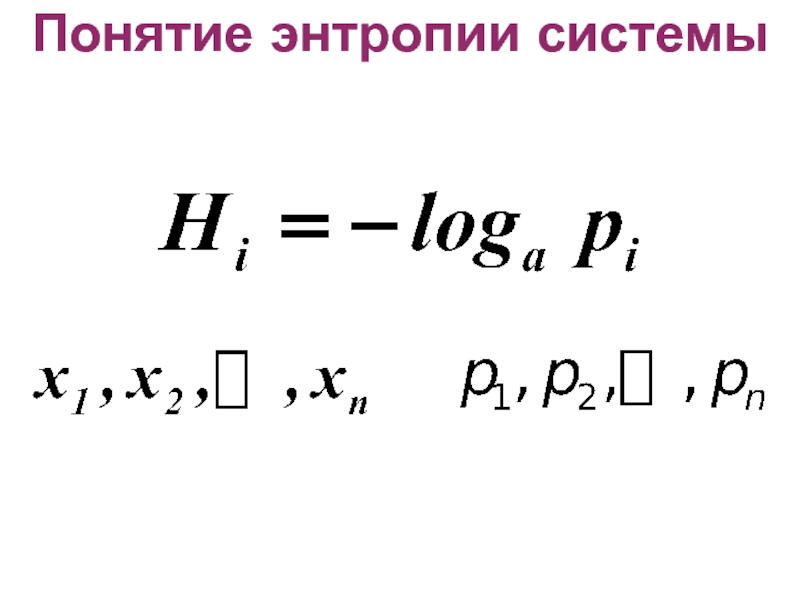Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистический подход Шеннона
Содержание
- 1. Статистический подход Шеннона
- 2. статистический подход Шеннона к измерению количества информации
- 3. статистический подход Шеннона (исходные позиции к измерению
- 4. Понятие энтропии системы
- 5. Понятие энтропии системыстепень неопределенности состояния (сообщения) i
- 6. Понятие энтропии системы
- 7. Понятие энтропии системы
- 8. Понятие энтропии системы энтропией системы(источника информации)называется сумма
- 9. Основные свойства энтропииЭнтропия всегда положительна, т.к.
- 10. Связь формулы Шеннона и формулы Хартли
- 11. Связь понятий энтропия и информацияестественно количество информации
- 12. Связь понятий энтропия и информацияколичество информации, приобретаемое
- 13. Единицы измерения количества информациибит binary unit
- 14. Единицы измерения количества информациитрит дит нат
- 15. Определение количества информации в сообщениичастная или собственная
- 16. Свойства частной информацииЧастная информация неотрицательна Частная информация,
- 17. частная и полная (средняя)информация
- 18. частная и полная (средняя)информацияЕсли все состояния системы
- 19. ВОПРОС ЗАКОНЧЕН
- 20. семантический подход к измерению количества информацииТезаурусная мера
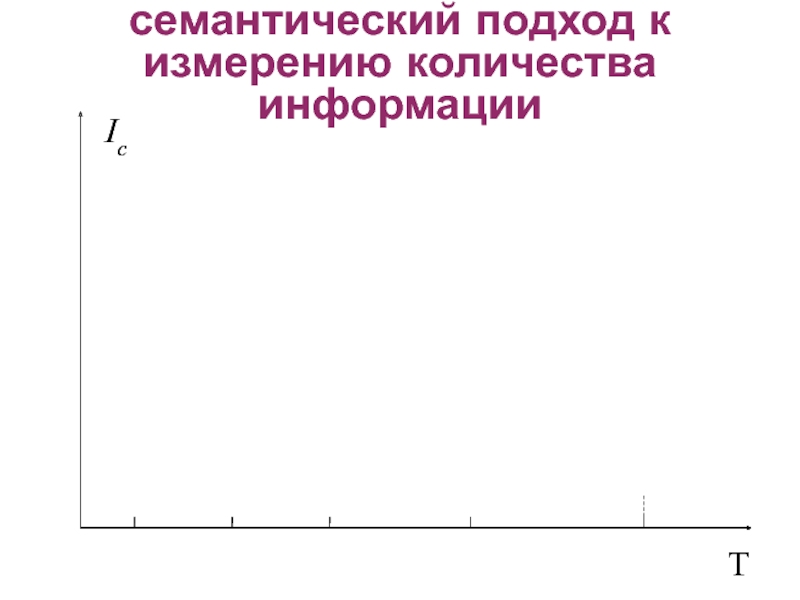
- 21. Ic TIc Tсемантический подход к измерению количества информации
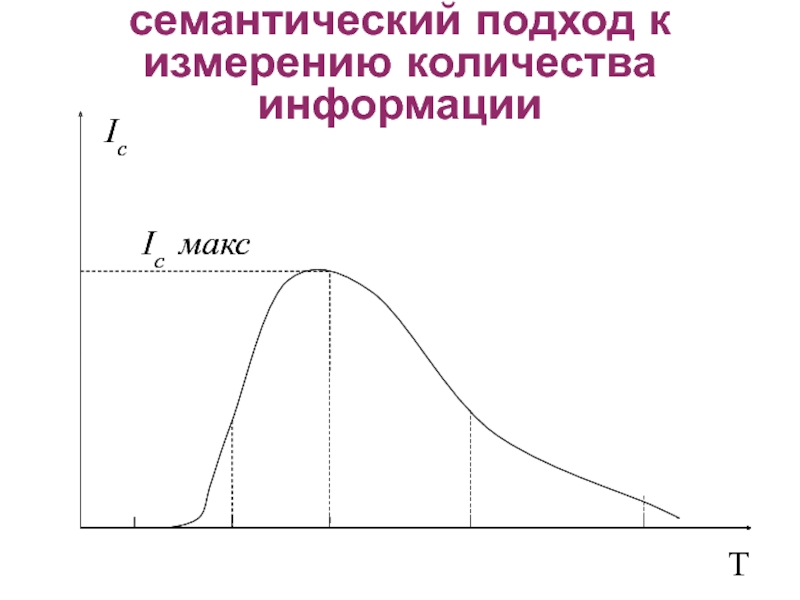
- 22. Ic максIc TIc максIc Tсемантический подход к измерению количества информации
- 23. Р. Карнапом и Бар–Хиллелом разработан подход к
- 24. прагматический подход к измерению количества информацииПрагматическая мера
- 25. Скачать презентанцию
статистический подход Шеннона к измерению количества информации
Слайды и текст этой презентации
Слайд 1ИНФОРМАЦИЯ И ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ.
ИЗМЕРЕНИЕ И КОДИРОВАНИЕ ИНФОРМАЦИИ
6. Измерение
информации
Слайд 3статистический подход Шеннона (исходные позиции к измерению количества информации)
определено количество
состояний системы (количество возможных сообщений)
для каждого сообщения определена вероятность его
появлениясистема описана как дискретная или непрерывная случайная величина
Слайд 5Понятие энтропии системы
степень неопределенности состояния (сообщения) i системы тем больше,
чем меньше его вероятность
степень неопределенности состояния i системы равна нулю,
если его вероятность равна 1 (система может принимать только одно состояние, значит она полностью определена);
Слайд 8Понятие энтропии системы
энтропией системы
(источника информации)
называется сумма произведений вероятностей различных
состояний системы на логарифмы их вероятностей, взятая со знаком минус
Слайд 9Основные свойства энтропии
Энтропия всегда положительна, т.к.
и логарифмы всегда отрицательны
Энтропия обращается в нуль, когда одно из состояний системы достоверно, а другие—невозможны
При увеличении числа состояний системы энтропия увеличивается
При заданном числе состояний энтропия обращается в максимум, когда эти состояния равновероятны
Энтропия обладает свойством аддитивности
Слайд 11Связь понятий энтропия и информация
естественно количество информации измерять уменьшением энтропии
той системы, для уточнения состояния которой предназначены сведения
X
H(X)
Слайд 12Связь понятий энтропия и информация
количество информации, приобретаемое при полном выяснении
состояния некоторой системы равно энтропии этой системы
Слайд 13Единицы измерения количества информации
бит binary unit binary digit
двоичная единица или бит, есть единица измерения степени неопределенности, представляющая
неопределенность, которая содержится в одном опыте, имеющем два равновероятных исхода 
Слайд 15Определение количества информации в сообщении
частная или собственная информация
X
xi
средняя или полная информация Ix представляется как математическое ожидание
(среднее) случайной величины,i-e значение которой есть собственная информация, получаемая от сообщения xi
Слайд 16Свойства частной информации
Частная информация неотрицательна
Частная информация, получаемая от сообщения
xi тем больше, чем меньше априорная вероятность pi получения этого
сообщенияЕсли сообщение имеет вероятность, равную единице, то информация, содержащаяся в нем, равна нулю
Частная информация обладает свойством аддитивности
Слайд 18частная и полная (средняя)информация
Если все состояния системы равновероятны, то частная
информация от каждого отдельного сообщения равна средней
(полной) информации о состоянии системы IxЕсли же система может принимает свои состояния с различными вероятностями, то информации от разных сообщений не одинаковы: наибольшую информацию несут сообщения о тех событиях, которые априори были наименее вероятны
Слайд 20семантический подход к измерению количества информации
Тезаурусная мера
Ю.А. Шрейдер
Тезаурус ?
Под
тезаурусом (от греческого сокровище) понимается некий обобщенный справочник, определяющий уровень
знаний получателя сообщений. Такой справочник включает не только описание понятий, но и связи между ними и т.д.
Слайд 23Р. Карнапом и Бар–Хиллелом разработан подход к определению количество семантической
информации на основе изменения логической вероятности.
Под логической вероятностью понимается
степень подтверждения той или иной гипотезысемантический подход к измерению количества информации
Слайд 24прагматический подход к измерению количества информации
Прагматическая мера определяет ценность информации,
ее полезность для достижения поставленной цели
А.А. Харкевич
