СТРОИТЕЛЬНАЯ МЕХАНИКА

(толщина) мало по сравнению с размерами самих поверхностей.
Плоскость, равноудаленная от

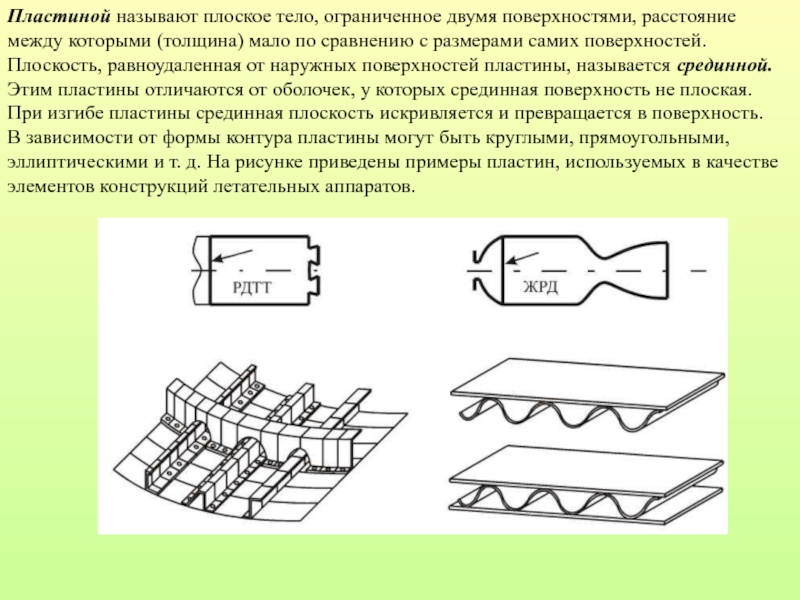
наружных поверхностей пластины, называется срединной. Этим пластины отличаются от оболочек, у которых срединная поверхность не плоская. При изгибе пластины срединная плоскость искривляется и превращается в поверхность.
В зависимости от формы контура пластины могут быть круглыми, прямоугольными, эллиптическими и т. д. На рисунке приведены примеры пластин, используемых в качестве элементов конструкций летательных аппаратов.

наименьшему размеру a в плоскости основания, пластины принято делить на

следующие группы:
Плиты или толстые пластины:
Тонкие пластинки:
Мембраны:

Геометрические особенности пластин различных групп позволяют принимать физически обоснованные только для них допущения, которые делают возможным упрощение системы уравнений теории упругости. Так, например, прогиб мембраны может в несколько раз превышать ее толщину, и можно сказать, что нормальные напряжения по толщине мембраны постоянные. В то же время тонкие пластинки получают прогиб, не превосходящий их толщины. Пластинки подобного типа широко распространены в технике, а их теория основана на гипотезах Кирхгоффа, которые позволяют существенно упростить систему уравнений теории упругости. Так как в конструкции ЛА в основном применяются пластины, подходящие под определение тонких далее будут рассматриваться только тонкие пластинки.

при расчете изгиба балок. В этих гипотезах принимается, что поперечные

сечения балки остаются плоскими и нормальными к ее оси в процессе изгиба. Дополнительно принимается, что волокна балки не надавливают друг на друга.

Для пластинок эти гипотезы формулируются следующим образом.
Первая гипотеза: нормаль к срединной поверхности не искривляется, а только поворачивается при изгибе пластинки. Это означает, что сдвиги в плоскостях, проходящих через нормаль к срединной поверхности, равны нулю. Следовательно, можно записать:

Вторая гипотеза: нормаль к срединной поверхности не растягивается, т. е.
Третья гипотеза: нормальными напряжениями на площадках, параллельных срединной плоскости, можно пренебречь по сравнению с другими напряжениями, т. е.

1. Основные гипотезы и уравнения. Изгиб пластин

окрестности любой точки пластинки элементарный параллелепипед, то на его гранях

будут действовать только напряжения σx, σy, τxy, τyx, а на срединной поверхности могут возникать только касательные напряжения τxy= τyx , т. к. на основании четвертой гипотезы нормальные напряжения здесь равны нулю, т. е. σx =σy=0.

Четвертая гипотеза: срединная поверхность не растягивается и не сжимается, т. е. нормальные напряжения на ней равны нулю.
Таким образом, с помощью гипотез Кирхгоффа можно трехмерное напряженное состояние свести к двумерному и сократить количество неизвестных в общей системе уравнений теории упругости.

систему уравнений теории упругости, воспользовавшись гипотезами Кирхгоффа. Установим сначала характер

изменения перемещений по толщине пластинки из геометрических уравнений теории упругости, которые в декартовой системе координат записываются так:

Проинтегрируем эти зависимости по z :

Здесь использовалось условие независимости w от z, w=w(x,y). Физически это означает, что толщина пластинки не меняется, а перемещения всех точек, имеющих одинаковые координаты в направлении оси z, равны.

основании которой на срединной поверхности, т. е. при z=0, u=v=0.

Тогда C1 =C2 = 0, и выражения принимают вид:

а геометрические уравнения можно переписать следующим образом:

физических уравнений. Имеем:
Подставляя в данные уравнения преобразованные геометрические уравнения получаем:
где

в последнее соотношение вместо модуля сдвига подставлено его выражение через модуль упругости:

объемные силы, останутся без изменений, т. к. в них присутствуют

производные от напряжений σz, τzx , τzy , которые соизмеримы с другими производными. В тоже время на основании гипотез Кирхгоффа величиной этих напряжений можно пренебречь из-за их малости по сравнению с другими напряжениями. Перепишем уравнения равновесия,

исключив из них проекции объемных сил:

Определим сначала из этих уравнений малые напряжения τzx, τzy, воспользовавшись физическими уравнениями. Имеем:

Интегрируем
их по z :

граничными условиями на поверхностях пластинки.
Нормалью к наружной поверхности (z=-h/2) пластинки

служит отрицательная ось z, поэтому nz=-1; nx=ny= 0 и, кроме этого, здесь Fnx=0 ; Fny=0; Fnz=q(x,y), поэтому из формул Коши получаем:

На внутренней поверхности пластинки при z=h/2: nz=1, nx=ny=0, Fnx=Fny= Fnz =0 и из формул Коши получаем:

Определяем константы интегрирования получаем:

уравнения :
подставляя в него производные
- бигармонический оператор
Проинтегрируем по z:
Для

определения константы C5(x,y) воспользуемся третьим граничным условием. Получим:

от τzx , τzy:

позволяют определить все напряжения в пластине, если известно перемещение w,

которое, как было установлено, не зависит от z.
Получим уравнение для определения w(x,y) из последнего выражения и ГУ.
Имеем:

или окончательно:

где

— цилиндрическая жесткость пластинки.

Уравнение равновесия изогнутой срединной поверхности пластинки в форме впервые было получено Софи Жермен

В цилиндрической системе координат

по поверхности пластинки, которые постоянны по ее толщине. Запишем теперь

окончательные выражения для напряжений по толщине пластинки.

Гипотезы Кирхгоффа позволили существенно упростить исходную систему уравнений теории упругости и получить следующие выражения для расчета напряжений в пластинке:

Как следует из выражений, напряжения σx, σy, τyx распределены по толщине пластинки линейно и равны нулю при z=0, т. е. на срединной плоскости. В то же время малые напряжения (принимаемые равными нулю на основании гипотез Кирхгоффа) τxz, τyz и σz распределены по толщине пластинки параболически. Причем нормальные напряжения σ, равны нулю при h/2 и по величине равны q(x,y) на внешней поверхности при z=-h/2 , где приложено внешнее изгибающее пластинку давление.

виде, введя понятия погонных усилий и моментов. Как известно, на

каждой грани пластинки будут действовать внутреннее усилие и момент, которые характеризуют воздействие отброшенной части тела на выделенную часть. Это усилие и момент можно разложить на три проекции по осям выбранной системы координат. В расчетах удобнее использовать не полное усилие и момент, действующие на грань пластинки, а их погонные значения (т. е. на единицу длины грани).
Таким образом, если на грани пластинки взять полоску единичной ширины и проинтегрировать выражения для напряжений по толщине пластинки, то это и будут погонные усилия. Интегрируя выражения для напряжений, получаем:

в выражениях для напряжений и погонных усилий получим выражения, связывающие

напряжения и погонные усилия:

Правило знаков: В дальнейшем будем считать, что перерезывающие силы и моменты положительные, если на той части грани пластинки, где z>0, они создают положительные напряжения.

ее перемещения w в направлении оси Z. Для определения w

необходимо решить уравнение Софи Жермен, к которому следует добавить граничные условия, следующие из условий закрепления пластинки по контуру.
Рассмотрим граничные условия для различных закреплений краев прямоугольной пластинки ОАВС, изображенной на рисунке.

1. Жесткая заделка на стороне ОА при у=0.
В заделке отсутствуют прогибы и невозможен поворот краевого сечения
относительно оси X, поэтому при у=0 должно быть w=0;
2. Шарнирно опертые края СО и АВ при х=0 и х=а.
На шарнирных краях перемещения и изгибающие моменты равны нулю, т. е. w = 0 и Мх = 0 . Последнее условие можно выразить через перемещение w с помощью полученной ранее формулы, поэтому граничные условия на шарнирно опертых краях СО и АВ принимают следующий вид: при х=0 и х=а должно быть w=0;

в ноль изгибающий момент Му, перерезывающая сила Qу и крутящий

момент Мxy , т. е. имеются три граничных условия вместо двух. Однако граничные условия для Qу и Мxy можно заменить одним эквивалентным граничным условием.
Для этого рассмотрим крутящий момент Н=Мхy= Мух, распределенный вдоль грани СВ, параллельной оси X (рис.а). На участке грани длиной dx действует крутящий момент, равный Hdx, который можно представить в виде двух вертикальных противоположно направленных сил Н с плечом dx (рис.б). На соседнем элементе крутящий момент будет больше, т. к. сила возрастает на бесконечно малую величину и равна


Его также можно представить в виде двух вертикально и противоположно направленных сил


плечом dx.

грани СВ. На границах каждого из бесконечно малых участков длиной

dx, за исключением крайних точек С и В, возникают две противоположно направленные силы, разность между которыми равна


а в точках С и В возникают сосредоточенные силы НС и НВ (рис. в).
Объединяя полученную вертикальную нагрузку с перерезывающей силой Qy, будем считать, что на грани СВ действует следующая приведенная погонная перерезывающая сила:

Следовательно, на свободном от закрепления крае СВ вместо трех условий Му=0; Qy=0; Мxy=0 можно потребовать выполнения лишь двух условий: Му=0 и Qy*=0, которые через перемещения записываются так: при у=b

не учитываются сосредоточенные силы в углах пластинки. Однако эффект их

воздействия в этих зонах на основании принципа Сен-Венана быстро затухает и не сказывается на напряженном состоянии всей пластинки.

Решим уравнение Софи Жермен для эллиптической пластинки, нагруженной равномерным давлением

при . Схема пластинки приведена на рисунке. В этом случае уравнение преобразуется к виду:

Граничные условия

т. е. перемещения и углы поворота равны нулю (защемление).

Уравнение и граничные условия будут удовлетворяться, если для прогиба принять следующее выражение:

где C — константа. Для ее определения подставим выражение для w решение в исходное уравнение.

решение уравнения Софи Жермен (функция прогиба) записывается следующим образом:

прогибом пластинки в ее центре. Если

, прогиб становится равным прогибу полоски шириной 2b, защемленной по концам.

Изгибающий и крутящий моменты определяются после подстановки выражения для прогиба в полученные ранее формулы. Так, для момента Mx находим:

Для центра пластинки и для конца большой полуоси эллипса получим соответственно:

Аналогично для момента My в центре и на концах малой оси эллипса находим:

Из полученных формул видно, что максимальные напряжения изгиба возникают на концах малой полуоси эллипса.

крутящий моменты в плоскости, нормальной к контуру пластинки. Эти погонные

моменты определяются выражениями для нормальных и касательных к контуру напряжений, полученных в результате поворота осей X и Y на угол α до совмещения оси X с нормалью n, а оси Y — с касательной t:

Изгибающий момент будет равен:

Угол α измеряется между осью X и нормалью n к контуру пластинки:

а крутящий:

шарнирно оперты, то решение ищется в виде двойного тригонометрического ряда:

При этом граничные условия на контуре удовлетворяются, а именно w=0 и Mx=0, My=0.
Нагрузка тоже представляется в виде:

где

подставляем в уравнение Софи Жермен

Граничные условия:

один его член, например, в случае· квадратной плиты, для прогиба

в центре дает

что отличается от точного решения на 2,5 %.

при сосредоточенном воздействии. Для этого представим сначала, что на ограниченном

участке действует распределенная нагрузка q0 = P/uv . В этом случае можно записать

Отсюда после интегрирования будем иметь

решение, определяющее прогиб пластины, нагруженной сосредоточенной силой в точке

краями
Решение ищется в виде тригонометрического ряда:

Каждый член ряда удовлетворяет ГУ.
Ym(y)

– искомая функция
Подставляем в уравнение Софи Жермен

Граничные условия:

Нагрузка представляется в виде:



где qm(y) можно получить следующим образом. Умножим правую и левую части выражения на sin(kπx/a)dx (k = 1, 2, 3, ...) и проинтегрируем результат по x от 0 до a.

это равенство справедливо при любых x, то, приравнивая множители при

синусах с одинаковыми номерами m, получим m уравнений

Решение каждого из этих уравнений имеет вид:

Частное решение Y*m определяется в зависимости от вида внешней нагрузки, а постоянные Am, Bm, Cm, Dm находятся из граничных условий на краях y=0, y=b.

представляется в виде конечного ряда

где задаваемые (аппроксимирующие) функции wi(х, у)

должны удовлетворять по крайней мере геометрическим граничным условиям. Неизвестные коэффициенты Аi определяются на основании условий типа

где полная потенциальная энергия Э вычисляется подстановкой фунции прогиба в виде ряда в функционал полной энергии

Условия минимума полной энергии приводят к системе линейных алгебраических уравнений, матричная форма которых имеет вид

k, элементы которых определяются по формулам

Определив из системы неизвестные коэффициенты

и подставив их в исходный ряд, получим искомую функцию прогибов. Точность результата зависит от количества рассчитываемых членов в ряде и характера выбранных аппроксимирующих функций. При практических расчетах пластин эти функции удобно представлять в виде

где φm(x) и ψn(y) – независимые ортогональные функции

упростятся как формулы для коэффициентов aij в уравнениях, так и

сами уравнения, так как матрица [a] станет диагональной и уравнения будут независимыми. В этом отношении в качестве функций φm(x) и ψn(y) можно рекомендовать формы собственных колебаний балки, соответствующей изолированной полоске, вырезанной из пластины вдоль осей x и у. Граничные условия для такой балки должны соответствовать условиям закрепления пластины на сторонах х=const и у=const. При выборе одного члена разложения в качестве функций φm(x) и ψn(y) можно взять форму статического прогиба полоски-балки при нагрузке, аналогичной нагрузке на пластину, или форму основного тона собственных колебаний если нагрузка на пластину равномерно распределенная.

что при одинаковой внешней нагрузке форма прогиба перфори-рованной пластинки подобна

форме изгиба сплошной пластинки.
Исходя из подобия кривых прогибов пластин, можно записать:

где γ — коэффициент пропорциональности, учитывающий снижение жесткости пластины из-за ее перфорации, а индексом ноль обозначено перемещение сплошной пластины, имеющей такую же жесткость, что и перфорированная пластина.
Значение коэффициента пропорциональности можно определять по формуле:

где d — диаметр отверстия; s — шаг отверстий; к — коэффициент жесткости пластинки: