Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СТРОИТЕЛЬНАЯ МЕХАНИКА
Содержание
- 1. СТРОИТЕЛЬНАЯ МЕХАНИКА
- 2. РЕКОМЕНДУЕМАЯ УЧЕБНО-МЕТОДИЧЕСКАЯ ЛИТЕРАТУРАкурса строительной механики
- 3. Строительная механика – наука, занимающаяся разработкой принципов
- 4. С точки зрения строительной механики под расчётом
- 5. СТРОИТЕЛЬНАЯмеханика Стержневых
- 6. 1. ТЕОРИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ 1.1 Теория
- 7. При совмещении направлений ρ, ρ1, ρ2 с
- 8. Соотношение Коши определяют шесть компонент деформаций через
- 9. 1.2 Теория напряженийИнтенсивность усилий, возни-кающих на выделенной
- 10. Основными законами, связывающими компоненты напряжений, являются уравнения
- 11. Полученные формулы показывают, что напряженное состояние в
- 12. Рассмотрим равновесие некоторой произвольной части тела. Пусть
- 13. Первые интегралы в этих равенствах берутся по
- 14. В скалярной форме формула имеет вид:где dV,
- 15. Полученные равенства должны тождественно выполняться для любого
- 16. Уравнения равновесия также могут быть получены и
- 17. Физические соотношенияФизические зависимости в линейной теории упругости
- 18. Подставляя значения упругих деформаций получим уравнения закона Гука при температурном воздействииили в форме, разрешенной относительно напряжений:
- 19. Таким образом, полная система уравнений теории упругости
- 20. 2. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ В ПЕРЕМЕЩЕНИЯХ И
- 21. Решение полученных уравнений должно удовлетворять граничным условиям:геометрические
- 22. Решение задачи в напряжениях Решение задачи в
- 23. Для того чтобы некая равновесная система деформаций
- 24. В результате преобразования с помощью уравнений равновесия,
- 25. Действительно, подставляя в условия совместности Сен-Венана функции
- 26. 3. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ УПРУГОЙ СИСТЕМЫРассмотрим непрерывное
- 27. Выделяя из тела бесконечно малый параллелепипед со
- 28. Подсчитаем сначала работу сил, действующих в направлении
- 29. Суммируя работу всех сил, представленных в таблице,
- 30. Приращение работы упругих сил, собранное со всей
- 31. Заменяя производные от приращений перемещений через приращения
- 32. Следует сделать оговорку о том, что введенное
- 33. 4. ВАРИАЦИОННОЕ РЕШЕНИЕ ЗАДАЧИ В ПЕРЕМЕЩЕНИЯХСогласно изложенному
- 34. 4.1 Полная энергия упругой системыДля построения вариационных
- 35. Преобразуем поверхностный интеграл J в объемный J1
- 36. Подставляя выражения для соответствующих интегралов, получим:Отметим, еще
- 37. 4.2 Вариационный принцип ЛагранжаВариационный принцип Лагранжа позволяет
- 38. Экстремальное значение функционала реализуется обращением в нуль
- 39. Так как перемещения должны быть кинематически возможными,
- 40. Сокращая первый и последний интегралы, окончательно получим:Поскольку
- 41. Минимизируя данный функционал методами вариационного исчисления, можно
- 42. 4.3 Пример1. Задача об изгибе балкиДля иллюстрации
- 43. Введем закон плоских сечений, согласно которому сечение
- 44. Согласно принципу Лагранжа и вариационного исчисления имеем:Интегрируя
- 45. Полученные уравнения являются уравнениями Эйлера — Лагранжа
- 46. Два первых уравнения являются уравнениями равновесия: первое
- 47. 5. ВАРИАЦИОННОЕ РЕШЕНИЕ ЗАДАЧИ В НАПРЯЖЕНИЯХВ соответствии
- 48. Подставляя функции деформации согласно закону Гука и
- 49. Таким образом, при отсутствии температурного воздействия для
- 50. 5.2 Вариационный принцип КастильяноВведем теперь по аналогии
- 51. Из равенств
- 52. Отметим, что объемные силы X, Y, Z,
- 53. Таким образом, в выражении для
- 54. Отметим, что согласно определения функции напряжений выражаются
- 55. Для аналитической записи принципа Кастильяно воспользуемся соотношением
- 56. 5.3 Принцип наименьшей работыНа практике обычно используется
- 57. Для реализации принципа наименьшей работы необходимо записать
- 58. 5.4 Пример 2. Стержневая системаРассмотрим стержневую систему,
- 59. Для определения усилий необходимо записать условие совместности
- 60. Решение с использованием принципа наименьшей работыИсходный функционалТак
- 61. Исключаем из выражения для дополнительной потенциальной энергии
- 62. 5.5 Теорема КастильяноБудем рассматривать произвольную деформируемую систему,
- 63. Дополнительная потенциальная энергия в рассматриваемом случае будет
- 64. 5.6 Пример 2. Стержневая система (продолжение)Покажем как
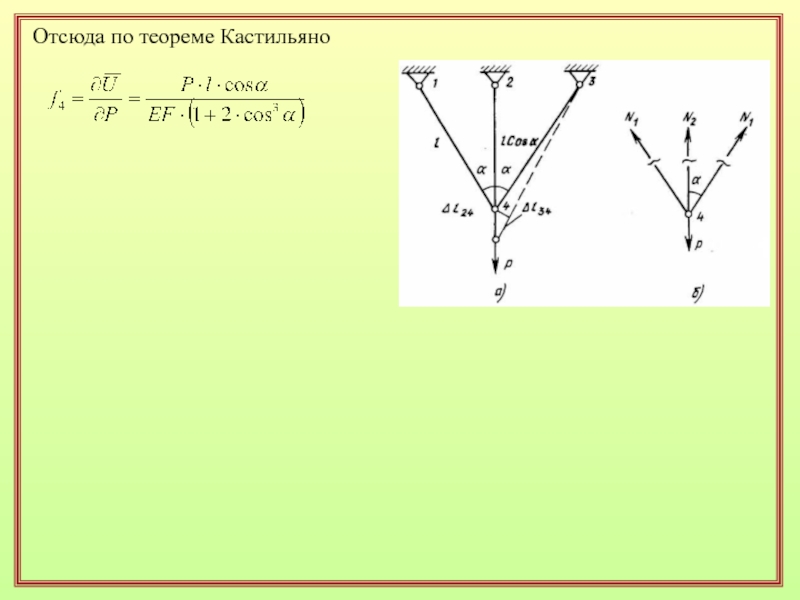
- 65. Отсюда по теореме Кастильяно
- 66. 5.7 Пример 3. Консольная балкаРассмотрим пример определения
- 67. Для определения дополнительной потенциальной энергии воспользуемся выражениемТак
- 68. Интеграл
- 69. 6. СМЕШАННЫЙ ВАРИАЦИОННЫЙ ПРИНЦИПВ предыдущих вопросах были
- 70. Согласно принципу наименьшей работы
- 71. Ввиду того, что вариации напряжений произвольны и
- 72. 7. Общие замечания относительно рассмотренных вариационных принципов.
- 73. Кроме того, введение в функционал системы гипотез,
- 74. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1СТРОИТЕЛЬНАЯ
МЕХАНИКА
Вводная лекция
Уравнения строительной механики
Вариационные принципы строительной механики
Доцент кафедры
«Самолетостроение»
Слайд 2
РЕКОМЕНДУЕМАЯ УЧЕБНО-МЕТОДИЧЕСКАЯ ЛИТЕРАТУРА
курса строительной механики
У ч е б н и к и:
1. Погорелов В.И. Строительная механика тонкостенных конструкций. СПб.: БХВ-Петербург, 2007.-528с.
Строительная механика летательных аппаратов: Учебник для авиационных специальностей/И.Ф.Образцов, Л.А. Булычев, В.В.Васильев и др. Под ред. И.Ф. Образцова. М.: Машиностроение, 1986. – 536с.
Дарков А.В., Шапошников Н.Н. Строительная механика. 2008 (2004,1987).
Электронные ресурсы :
1. http://www.stroitmeh.ru/ Сайт к.т.н., доцента кафедры теоретической и прикладной механики Каримова Ильдара
2. Савельев, Л. М. Строительная механика летательных аппаратов [Электронный ресурс] : электрон. учеб. пособие / Л. М. Савельев, Ю. В. Скворцов, С. В. Глушков; Минобрнауки России, Самар. гос. аэрокосм. ун-т им. С. П. Королева (Нац. исслед. ун-т).– Самара, 2011.
Слайд 3Строительная механика –
наука, занимающаяся разработкой
принципов и методов расчёта
сооружений и конструкций,
представляющих собой системы,
состоящие из элементов различных
типов(стержневые, пластинчато-оболочечные, массивные)
на прочность, жёсткость и устойчивость
при статических и динамических воздействиях
с учётом требований
надёжности и экономичности.
Слайд 4
С точки зрения строительной механики
под расчётом конструкции в целом
или ее составляющих частей
понимается определение параметров
напряжённо-деформированного состояния –
силовых факторов и перемещений, необходимых для оценки прочности,
жёсткости и устойчивости.
Слайд 5СТРОИТЕЛЬНАЯ
механика
Стержневых Пластин
Комбинированных
систем и оболочек
системМатематика
Детали машин
И механизмов
Конструкция самолета
Прочность конструкции самолета
Специальные
дисциплины
МЕЖПРЕДМЕТНЫЕ СВЯЗИ
СТРОИТЕЛЬНОЙ МЕХАНИКИ
И ЕЁ РОЛЬ В ПОДГОТОВКЕ
СПЕЦИАЛИСТА
Физика
Теоретическая
механика
Термодинамика
Информатика
Сопротивление
материалов
Теория упругости,
пластичности
и ползучести
Слайд 61. ТЕОРИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ
1.1 Теория деформаций
Обозначим компоненты смещения произвольной
точки тела с декартовыми координатами х, у, z через и,
v, w. Тогда перемещение R по произвольному направлению ρ, определенному направляющими косинусами l, m, n ( , , ), будет равно:Примем, что возникающие относительные деформации настолько малы, что ими можно пренебречь в сравнении с единицей. В этом случае линейная деформация ερ и угловая γρ1ρ2 между двумя взаимно ортогональными направлениями ρ1 и ρ2 определяются формулами:
Слайд 7При совмещении направлений ρ, ρ1, ρ2 с координатами х, у,
z из формул следуют геометрические соотношения Коши:
Рассматривая формулу, для перемещения
R в направлении ρ как сложную функцию, от координат запишем ее производную:и, используя геометрические соотношения Коши, получим:
Данные формулы с одной стороны, преобразуют компоненты деформаций к деформациям в новых осях, а, с другой, показывают, что шесть компонент деформаций εx, εy, εz, γxy, γyz, γxz полностью определяют деформацию тела в точке в любой ортогональной системе координат ρ, ρl, ρ2.
Слайд 8Соотношение Коши определяют шесть компонент деформаций через частные производные от
трех функций u, v, w. Отсюда следует, что сами деформации
как функции координат не являются независимыми и должны быть связаны между собой некоторыми соотношениями, которые называются уравнениями совместимости деформаций.Эти уравнения могут быть получены из соотношений Коши в результате исключения перемещений и, v, w, и носят названия условия совместности деформаций Сен-Венана. Последовательность их получения была рассмотрена в дисциплине «Сопротивление материалов». Они имеют следующий вид:
Справедливость данных выражений может быть проверена подстановкой выражений для деформаций из соотношений Коши, в результате которой они обращаются в тождества.
Слайд 91.2 Теория напряжений
Интенсивность усилий, возни-кающих на выделенной внутри тела произвольной
площадке, представ-ляется в виде трех компонент напряжений — нормального и
двух касательных, действующих во взаимоортогональных направлениях.Определяя направление ρi направляющими косинусами
, ,
можно выразить компоненты напряжений σρ, τρρ1, τρρ2 через проекции суммарного напряжения σ на оси х, у, z, то есть:
Слайд 10Основными законами, связывающими компоненты напряжений, являются уравнения равновесия. Для получения
их выделим из тела элементарный тетраэдр и рассмотрим его равновесие.
Составляя суммы проекции всех сил, действующих по граням тетраэдра на три оси получим:касательных напряжений τxy=τyx, τyz=τzy, τzx=τxz в силу которого порядок индексов у касательных напряжений становится безразличным.
Здесь l, т, п — направляющие косинусы нормали к наклонной площадке.
Суммы моментов всех сил относительно трех осей дают закон парности
Получим зависимости, определяющие напряжения в произвольной ортогональной системе координат. Подставляя Xρ, Yρ, Zρ из полученных равенств в выражения для σρ, τρρ1, τρρ2 , получим:
Слайд 11Полученные формулы показывают, что напряженное состояние в произвольной точке тела
полностью определяется шестью компонентами напряжений (с учетом парности касательных напряжений),
действующих на трех взаимно перпендикулярных площадках.Располагая элементарный тетраэдр у поверхности тела, чтобы косая грань совместилась с элементом поверхности тела, и в силу этого считая, что компоненты Хρ, Yρ, Zρ определяют
которые называются условиями на поверхности и являются статическими граничными условиями.
поверхностную нагрузку (Хρ=Xv, Yρ=Yv, Zρ=Zv, v - нормаль к поверхности), получим три алгебраических соотношения:
Слайд 12Рассмотрим равновесие некоторой произвольной части тела. Пусть объем этой части
v и силы, действующие на каждую единицу объема, заданы компонентами
X, Y, Z внешняя поверхность этой части S1 и поверхностные силы на ней — Xv, Yv, Zv. Поверхность, которой отсекается произвольная часть тела, обозначим через S2.Cилы, действующие на нее, через Хρ, Yρ, Zρ. Составляя суммы проекций всех сил, действующих на рассматриваемую произвольную часть тела, получим:
К левой части первого уравнения прибавим и вычтем , к левой части второго уравнения - , третьего уравнения - , получим:
Слайд 13Первые интегралы в этих равенствах берутся по полной поверхности рассматриваемой
части тела и на основании теоремы Остроградского-Гаусса могут быть преобразованы
в объемные.Или, с учетом свойств интегралов по поверхности:
Формула Гаусса – Остроградского – математическая формула, которая выражает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объему, ограниченному этой поверхностью:
то есть интеграл от дивергенции векторного поля , распространённый по некоторому объёму V, равен потоку вектора через поверхность S, ограничивающую данный объём.
Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.
Слайд 14В скалярной форме формула имеет вид:
где dV, dS – дифференциалы
объема и поверхности соответственно, l, m, n –направляющие косинусы, P=P(x,y,z),
Q=Q(x,y,z), R=R(x,y,z) – функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.Подставляем в уравнения выражения для Хρ, Yρ, Zρ
используем формулу Остроградского-Гаусса, получим
Слайд 15Полученные равенства должны тождественно выполняться для любого объема v, выделенного
из тела и при любой внешней поверхности S1, а это
возможно лишь при тождественном равенстве нулю подынтегральных выражений, что дает уже полученные нами ранее три условия на поверхности и три дифференциальных уравнения равновесия:Слайд 16Уравнения равновесия
также могут быть получены и непосредственно как
условия равновесия бесконечно малого элемента, выделенного из тела и показанного
на рисунке, как это делалось в дисциплине «Сопротивление материалов»Слайд 17Физические соотношения
Физические зависимости в линейной теории упругости для изотропного тела
представлены уравнениями обобщенного закона Гука в напряжениях и деформациях, имеющими
вид:или в обратной форме
В формулах — объемная деформация, Е и G — модуль упругости и модуль сдвига; μ, λ — коэффициенты Пуассона и Ламе, между которыми имеются следующие зависимости:
При температурном воздействии уравнения закона Гука преобразуются на основании гипотез Франца Неймана, постулирующих, что полные линейные деформации εх, εу, εz связаны с перемещениями формулами Коши, а упругие деформации связаны с напряжениями уравнениями обобщенного закона Гука. Под полными деформациями понимаются сумма упругих εyх, εyу, εyz и чисто температурных деформаций αt, т. е.
Слайд 18Подставляя значения упругих деформаций получим уравнения закона Гука при температурном
воздействии
или в форме, разрешенной относительно напряжений:
Слайд 19Таким образом, полная система уравнений теории упругости включает 15 уравнений:
три уравнения равновесия,
- шесть геометрических соотношений Коши или вытекающих из
них уравнений совместимости деформаций шесть соотношений закона Гука.
Эта система включает 15 неизвестных: шесть напряжений, шесть относительных деформаций и три перемещения, т. е. является полной. Решение основной системы должно удовлетворять граничным условиям на поверхности тела — статическим или геометрическим, которые формулируются через перемещения.
Слайд 202. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ В ПЕРЕМЕЩЕНИЯХ И В НАПРЯЖЕНИЯХ
В теории
упругости используются две классические формы записи разрешающих уравнений, к которым
сводится полученная полная система 15 уравнений.2.1 Решение задачи в перемещениях
Решение задачи в перемещениях предусматривает введение в качестве неизвестных, определяемых, в первую очередь, трех функций перемещений и(х, у, z), v(х, у, z), w(х, у, z).
Выражая в законе Гука деформации через перемещения с помощью геометрических соотношений и подставляя полученные выражения для напряжений в уравнение равновесия, получим три уравнения равновесия в перемещениях (уравнения Ламе):
где
Слайд 21Решение полученных уравнений должно удовлетворять граничным условиям:
геометрические граничные условия (перемещения
отдельных точек тела) накладываются непосредственно на перемещения,
статические граничные условия
(усилия на поверхности тела) записываются через перемещения с помощью равенств и
По найденным в результате решения системы уравнений перемещениям могут быть далее определены деформации и напряжения, т. е. получено полное решение задачи.
Слайд 22Решение задачи в напряжениях
Решение задачи в напряжениях предусматривает введение
в качестве основных неизвестных шести компонент напряжений, которые должны удовлетворять
трем уравнениям равновесияПоскольку три уравнения с шестью неизвестными могут иметь множество решений, существует множество систем напряжений, удовлетворяющих уравнениям равновесия. Такие системы напряжений называются равновесными. Для того чтобы выделить из статически возможных систем истинную систему напряжений, будем рассуждать следующим образом. Пусть имеется некоторая равновесная система напряжений. Тогда деформация однозначно определяются из закона Гука и для завершения решения необходимо найти перемещения. Однако при этом надо проинтегрировать шесть геометрических уравнений, включающих три неизвестных перемещения, т. е. систему в общем случае несовместную.
Слайд 23Для того чтобы некая равновесная система деформаций
была совместной, необходимо,
чтобы деформации были связаны некоторыми соотношениями, которые и были получены
выше в форме условий совместности Сен-ВенанаТаким образом, истинные напряжения отличаются от всех равновесных тем, что вызываемые ими деформации удовлетворяют уравнениям совместности деформаций Сен-Венана. Эти уравнения с помощью закона Гука могут быть записаны через напряжения.
Слайд 24В результате преобразования с помощью уравнений равновесия, в которых отсутствуют
объемные силы, уравнения совместности деформаций могут быть приведены к виду
Здесь
Таким
образом, основная система уравнений для решения задачи в напряжениях включает уравнения равновесия (при X=Y=Z=0) и представленные выше уравнения совместности деформаций. Отметим, что полученная система включает девять уравнений, содержащих шесть неизвестных функций напряжений. Из вывода уравнений совместности следует, что всегда существует три дополнительные функции, которые позволяют тождественно удовлетворять эти уравнения. Такими функциями являются, например, перемещения u, v и w.Слайд 25Действительно, подставляя в условия совместности Сен-Венана функции деформации, выраженные с
помощью геометрических соотношений Коши через три произвольные функции u, v,
w, можно убедиться в том, что уравнения совместности Сен-Венана, а, следовательно, и полученные из них разрешающие уравнения задачи в напряжениях тождественно удовлетворяются при любых функциях и, v и w.Например:
По найденным в результате решения системы разрешающих уравнений напряжениям с помощью закона Гука определяются деформации, а затем из системы геометрических соотношений Коши (которая в силу того, что условия ее интегрируемости удовлетворены, является совместной) находятся перемещения. Построенное решение подчиняется граничным условиям — статическим в форме или геометрическим, которые накладываются на найденные перемещения.
Слайд 263. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ УПРУГОЙ СИСТЕМЫ
Рассмотрим непрерывное упругое тело, находящееся
под внешним силовым и температурным воздействием. В силу того, что
в теле при этом возникают напряжения и деформации, в нем накапливается потенциальная энергия деформации, измеряемая работой упругих сил П.Для определения работы упругих сил рассмотрим ее приращение в функции от приращения перемещений δu, δv, δw. Тогда, рассматривая тело как совокупность бесконечно малых параллелепипедов, заполняющих внутренний объем, и бесконечно малых тетраэдров, определяющих пограничную зону, прилегающую к поверхности, подсчитываем работу, совершаемую в каждой элементарной его части.
Слайд 27Выделяя из тела бесконечно малый параллелепипед со сторонами dx, dy,
dz и заменяя влияние отброшенных частей напряжениями, получим на его
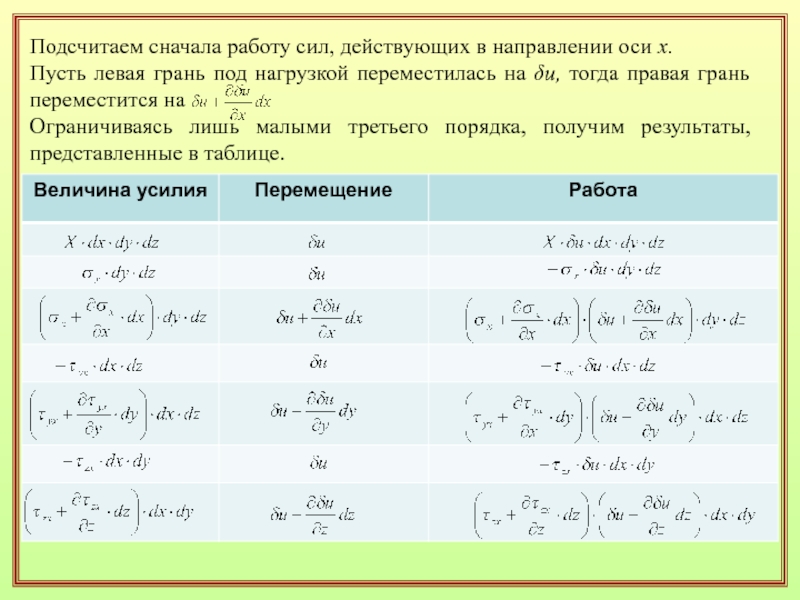
внешних гранях интенсивность сил, представленную на рисунке. Кроме того, будем считать, что на каждую единицу объема действуют объемные силы, заданные компонентами X, Y, Z. Зададим приращения перемещений δu, δv, δw, непрерывно меняющиеся от точки к точке.Слайд 28Подсчитаем сначала работу сил, действующих в направлении оси х.
Пусть левая
грань под нагрузкой переместилась на δu, тогда правая грань переместится
наОграничиваясь лишь малыми третьего порядка, получим результаты, представленные в таблице.
Слайд 29Суммируя работу всех сил, представленных в таблице, найдем:
Аналогичным образом подсчитывая
работу всех сил, действующих вдоль осей у и z, получим:
Таким
же образом подсчитываем работу сил, действующих на тетраэдр, в котором наклонная грань предполагается совпадающей с внешней поверхностью, и в силу этого действующая на ней нагрузка определяется поверхностными силами Хρ=Xv, Yρ=Yv, Zρ=Zv. В результате найдем:Слайд 30Приращение работы упругих сил, собранное со всей совокупности параллелепипедов и
тетраэдров, выразится теперь так:
Подставляя сюда найденные выше приращения элементарных работ,
получим:Для тела, находящегося в состоянии равновесия, два первых интеграла в силу уравнений равновесия обращаются в нуль.
Слайд 31Заменяя производные от приращений перемещений через приращения деформаций с помощью
соотношений Коши, окончательно будем иметь:
В задачах строительной механики вводится гипотеза
о существовании потенциала упругих сил, заключающаяся в том, что работа упругих сил П полностью переходит в потенциальную энергию U, накапливаемую телом при деформации, т. е. δП=δU. Если ввести понятие удельной потенциальной энергии W, как энергии, отнесенной к единице объема, то:Сопоставляя формулы выше можно сделать вывод:
С другой стороны, в силу существования потенциала упругих сил потенциальная энергия есть функция только деформаций и, следовательно, ее приращение равно:
Сопоставление выражений для δW приводит к формулам Грина
являющимся аналитическим выражением гипотезы о существовании потенциала упругих сил.
Слайд 32Следует сделать оговорку о том, что введенное понятие упругого потенциала
в рамках термоупругой задачи закономерно лишь при определенном ограниченном уровне
температуры, при котором в потенциальной энергии можно пренебречь чисто температурными членами в силу их малости. Кроме того, в дальнейших выкладках рассматриваются лишь такие температурные задачи, когда температура не зависит от деформации, а модули упругости — от температуры. При сделанном замечании удельная потенциальная энергия будет определяться интегрированием выражения для δW т. е.Внося сюда выражение для δW, подставляя напряжения из закона Гука и производя интегрирование, получим выражение для удельной потенциальной энергии, записанное через деформации:
Используя выражения для деформаций из закона Гука можно получить удельную потенциальную энергию, записанную в смешанной форме:
Слайд 334. ВАРИАЦИОННОЕ РЕШЕНИЕ ЗАДАЧИ В ПЕРЕМЕЩЕНИЯХ
Согласно изложенному выше истинные напряжения,
деформации и перемещения, реализующиеся в упругой системе, удовлетворяют полной системе
уравнений теории упругости, содержащей статические, геометрические и физические соотношения.Введенное понятие потенциальной энергии упругой системы позволяет дополнительно сформулировать некоторые энергетические свойства истинного напряженно-деформированного состояния, реализация которых эквивалентна удовлетворению отдельных групп основной системы уравнений. Эти энергетические свойства устанавливаются вариационными принципами, которые широко используются в строительной механике.
Слайд 344.1 Полная энергия упругой системы
Для построения вариационных принципов потребуется понятие
полной энергии Э, которую формально введем как разность между потенциальной
энергией и работой внешних сил:Здесь U - потенциальная энергия деформации и А - работа внешних сил, определяемая формулой:
Здесь Xv, Yv, Zv — компоненты поверхностной нагрузки, а X, Y, Z — компоненты объемной нагрузки, интегрирование осуществляется соответственно по поверхности тела S и объему V.
Преобразуем выражение для работы внешних сил А. Для этого введем некоторую произвольную систему напряжений и систему перемещений (не обязательно соответствующую напряжениям ) и рассмотрим следующий поверхностный интеграл:
Каждое слагаемое данного интеграла подходит для использования в формуле Остроградского-Гаусса
Слайд 35Преобразуем поверхностный интеграл J в объемный J1 на основании формулы
Остроградского-Гаусса:
и, кроме того, введем в рассмотрение объемный интеграл J2, включающий
произвольную систему малых деформаций не связанную ни с компонентами перемещений, ни с компонентами напряжений:Очевидно, выражение работы внешних сил A не изменится, если к нему прибавить и вычесть одни и те же величины. Пользуясь этим, напишем:
Слайд 36Подставляя выражения для соответствующих интегралов, получим:
Отметим, еще раз, что входящие
в данное выражение компоненты перемещений, деформаций и напряжений совершенно произвольны
и не соответствуют действительно возникающим в теле деформированному и напряженному состоянию при нагружении.Слайд 374.2 Вариационный принцип Лагранжа
Вариационный принцип Лагранжа позволяет сформулировать энергетический признак,
выделяющий истинную систему перемещений, возникающую в теле.
Формулировка вариационного принцип
Лагранжа: из всех кинематически возможных систем перемещений в действительности в упругой системе реализуются лишь те, которые сообщают минимум полной энергии. Под кинематически возможными здесь понимаются перемещения, удовлетворяющие геометрическим граничным условиям на поверхности тела и связанные с относительными деформациями соотношениями Коши.
Таким образом, согласно принципу Лагранжа полная энергия тела, в котором имеет место действительное поле перемещений, должна быть минимальной. При этом деформируемая система должна быть консервативной, т. е. приращение потенциальной энергии должно являться полным дифференциалом от приращения деформаций, а внешние силы не зависеть от перемещений. Поскольку полная энергия Э=U-A выражается через интегралы, она является функционалом и согласно вариационному исчислению реализация принципа Лагранжа сводится к задаче минимизации функционала. Докажем правомочность сформулированной вариационной задачи.
Слайд 38Экстремальное значение функционала реализуется обращением в нуль главной линейной части
приращения функционала — первой вариации:
причем, если вторая вариация меньше нуля,
то имеет место минимум. Можно показать, что в рассматриваемых задачах реализуется именно минимум.Раскрывая выражение для полной энергии имеем
Входящую в данное выражение вариацию потенциальной энергии деформации δU можно определить используя полученные ранее равенства
Для записи вариации работы внешних сил δА воспользуемся соотношением
Слайд 39Так как перемещения должны быть кинематически возможными, то, следовательно, должны
удовлетворяться соотношения Коши и третий интеграл в выражении для A
равен нулю.Выражение для работы внешних сил упрощается
Кроме того, положим , , и соответственно ,.., . Тогда выражение для полной энергии примет вид:
Слайд 40Сокращая первый и последний интегралы, окончательно получим:
Поскольку вариации δи, δv,
δw произвольны и взаимно независимы, из данного выражения вытекают полученные
ранее уравнения равновесия и статические граничные условия, что и доказывает справедливость принципа.Для реализации вариационного принципа Лагранжа в задачах в перемещениях необходимо записать условия минимума полной энергии Э, выраженной через перемещения.
Подставляя в равенство Э=U-A , где W выражено через деформации
в которой функции деформации выражены через перемещения с помощью соотношений Коши и работу внешних сил А согласно зависимости
окончательно будем иметь:
Слайд 41Минимизируя данный функционал методами вариационного исчисления, можно получить три уравнения
относительно функций u, v, w и естественные граничные условия, которые
совпадают соответственно с уравнениями равновесия в перемещениях и статическими граничными условиями, записанными через перемещения. Таким образом, принцип Лагранжа является вариационным аналогом метода решения в перемещениях.Полученному равенству можно придать и другую трактовку, если считать δu, δv и δw малыми возможными перемещениями тела в состоянии равновесия. В этом случае равенство описывает принцип возможных перемещений, согласно которому в состоянии равновесия сумма работ всех внешних и внутренних сил должна быть равна нулю. При этом требование консервативности системы отпадает.
Слайд 424.3 Пример1. Задача об изгибе балки
Для иллюстрации принципа Лагранжа рассмотрим
задачу об изгибе балки, показанной на рис. В этом случае
отличны от нуля перемещения и(х, у), v (х, у), а интегралы в функционале берутся по длине балки и сечению с площадью F.Полагая w, t=0, X=Y=Z=0 (сил инерции и тяжести нет), Xv=Zv=0, Yv=q (распределенная поверхностная нагрузка только вертикальная) получим:
Исходный функционал
Слайд 43Введем закон плоских сечений, согласно которому сечение х=const не деформируется
вдоль оси у и остается плоским и нормальным к нейтральной
оси у=0. Отсюда следует, что:Интегрируя эти уравнения, получим:
Пренебрегая эффектом Пуассона, который не учитывается в энергии изгиба балок (μ=0), и подставляя перемещение u в функционал, будем иметь:
где, например, v'= dv/dx, J — центральный момент инерции сечения. Выражение представляет собой функционал, который символически записывается в следующем виде:
Слайд 44Согласно принципу Лагранжа и вариационного исчисления имеем:
Интегрируя по частям дважды
второе слагаемое под знаком интеграла и один раз третье, получим:
Полученное
выражение будет тождественно равно нулю при произвольных вариациях перемещений δv и δu0 лишь тогда, когда подынтегральные выражения и внеинтегральные члены будут равны нулю, т. е.:Слайд 45Полученные уравнения являются уравнениями Эйлера — Лагранжа для рассматриваемого функционала,
а внеинтегральные члены — естественными граничными условиями. Для ряда задач
уравнения Эйлера—Лагранжа и естественные граничные условия могут быть взяты в готовом виде из курсов вариационного исчисления.Вычислим входящие в данные уравнения производные:
Вносим эти производные в уравнения Эйлера-Лагранжа, получим:
Для истолкования полученных соотношений напомним, что согласно сопротивлению материалов в сечении балки действуют изгибающий момент М, перерезывающая сила Q и осевая сила N, которые определяются формулами:
С учетом этого соотношения полученные выше соотношения принимают вид
Слайд 46Два первых уравнения являются уравнениями равновесия: первое — уравнением упругой
линии балки, а второе — уравнением растяжения оси. Три последних
равенства определяют граничные условия. Если перемещения u0, v и угол поворота v' на крае балки заданы, то вариации и условия заданные в данных равенствах удовлетворяются автоматически. На свободном крае кинематические факторы не заданы, их вариации отличны от нуля и согласно этих равенств получим М=Q=N=0, т. е. статические граничные условия. Таким образом, полученные соотношения включают уравнения равновесия и статические граничные условия, записанные через перемещения.Слайд 475. ВАРИАЦИОННОЕ РЕШЕНИЕ ЗАДАЧИ В НАПРЯЖЕНИЯХ
В соответствии с изложенным ранее
при решении задачи в напряжениях истинное поле напряжений выделяется из
статически возможных путем удовлетворения уравнений неразрывности деформаций. Аналогами этих уравнений при энергетической постановке являются вариационные принципы, вводимые на основании понятия дополнительной энергии.5.1 Дополнительная потенциальная энергия
Введем по аналогии понятие дополнительной потенциальной энергии деформации:
причем приращение удельной дополнительной энергии будем связывать с приращениями напряжений
для сравнения
Слайд 48Подставляя функции деформации согласно закону Гука и интегрируя, получим:
Дифференцирование данного
выражения по компонентам напряжений дает формулы Кастильяно, свидетельствующие о том,
что дополнительная удельная потенциальная энергия является потенциалом упругих деформаций:Для того чтобы выявить соотношение между удельной потенциальной энергией W, и дополнительной энергией , рассмотрим одноосное растяжение стержня вдоль его оси х при отсутствии температурного воздействия. В этом случае все компоненты напряжений, за исключением σх, обращаются в нуль и согласно выражения на предыдущем слайде имеем
Из закона Гука имеем σх = Е∙εх
Слайд 49Таким образом, при отсутствии температурного воздействия для линейно-упругого тела
. Из геометрического смысла интегралов следует, что W
и в рассматриваемом случае представляют собой площади треугольников, показанных на рисунке а. Для нелинейно упругого материала W и не совпадают (рис. б).Слайд 505.2 Вариационный принцип Кастильяно
Введем теперь по аналогии выражение полной энергии,
записанной через дополнительную энергию
Основной закон, позволяющий строить решение задачи в
напряжениях, сформулирован Кастильяно в виде следующего принципа: из всех статически возможных систем напряжений в действительности в упругой системе возникают лишь те, которые сообщают стационарное (минимальное) значение полной энергии, записанной через дополнительную потенциальную энергию. Поскольку полная энергия есть функционал, то условием стационарности его является обращение в нуль первой вариации:
Напомним, что статически возможными называются системы напряжений, удовлетворяющие уравнениям равновесия и условиям на поверхности. Будем считать также, что напряжения связаны с деформациями законом Гука. Тогда для решения задачи в напряжениях необходимо удовлетворить уравнения совместности деформаций Сен-Венана.
Покажем, что эти уравнения можно получить из принципа Кастильяно.
Слайд 51Из равенств
и имеем:
Находим
выражение для из зависимостейВыражение для получаем варьируя напряжения в зависимости для А. Получаем:
Слайд 52Отметим, что объемные силы X, Y, Z, входящие в уравнения
равновесия и в первый интеграл полученного выражения, являются заданными и,
следовательно, их вариации равны нулю. Что касается поверхностных сил Xv, Yv, Zv, то статические возможные системы напряжений не обязательно должны сводиться на поверхности тела к заданным нагрузкам и можно ввести их вариации, напримерТогда поверхностный интеграл в полученном выражении исчезает. Для того чтобы входящие в полученное выражение компоненты напряжений были статически возможными, введем в рассмотрение шесть функций напряжений φt, связанных с компонентами напряжений следующими зависимостями:
Непосредственной подстановкой этих выражений в первый интеграл выражения для можно убедиться, что он обращается в нуль благодаря тому, что введенное выражение для напряжений тождественно удовлетворяет уравнения равновесия.
Слайд 53Таким образом, в выражении для остается
только последний интеграл, который принимает вид:
Отметим, что при варьировании функций
напряжений, интегралы, содержащие объемные силы, исчезают, так как последние не варьируются.Преобразуем полученное выражение интегрированием по частям. Например, для первого члена будем иметь:
Слайд 54Отметим, что согласно определения функции напряжений выражаются через вторые производные
от функций напряжений. Значения их первых производных и самих функций
φi на границе тела несущественны и могут быть приняты равными нулю. Таким образом, поверхностный интеграл может быть отброшен и выражение для принимает вид:В силу произвольности вариации функций напряжений отсюда вытекают уравнения совместимости деформаций Сен-Венана. Таким образом доказано, что уравнение при удовлетворении уравнений равновесия эквивалентно уравнениям совместимости деформаций, т. е. принцип Кастильяно является энергетическим аналогом метода решения задачи теории упругости в напряжениях.
Слайд 55Для аналитической записи принципа Кастильяно воспользуемся соотношением
Применяя к первому
интегралу формулу Остроградского и учитывая, что δХ=δF=δZ=0, окончательно получим:
Тут первый
интеграл представляет собой вариацию , а второй — работу вариаций поверхностных нагрузок.Слайд 565.3 Принцип наименьшей работы
На практике обычно используется частная форма записи
принципа Кастильяно, называемая принципом наименьшей работы или принципом минимума дополнительной
потенциальной энергии. Предположим, что сравниваются не все статически возможные системы напряжений, а те из них, которые сводятся на поверхности тела к заданным нагрузкам Xv, Yv, Zv. Тогда и изс учетом
и
получим
Полученный результат и является принципом наименьшей работы и формулируется следующим образом: из всех статически возможных систем напряжений, сводящихся на поверхности тела к заданным нагрузкам, в действительности в упругой системе возникают лишь те, которые сообщают экстремальное (минимальное) значение дополнительной потенциальной энергии.
Слайд 57Для реализации принципа наименьшей работы необходимо записать условие минимума дополнительной
потенциальной энергии, выраженной через напряжения.
Согласно равенствам
получим:
Здесь входящие функции напряжений должны удовлетворять уравнениям равновесия и статическим граничным условиям. Минимизация данного функционала методами вариационного исчисления приводит к системе уравнений, которые являются уравнениями совместимости деформаций, записанными через напряжения.
Слайд 585.4 Пример 2. Стержневая система
Рассмотрим стержневую систему, показанную на рис.
а. При действии силы Р в стержнях возникают нормальные напряжения,
которые распределены равномерно по сечению и длине стержней и обычно заменяются усилиями в стержнях (F — площадь сечения, которая считается одинаковой длявсех стержней так же, как и модуль упругости материала Е). В силу симметрии усилия в стержнях 1 ... 4 и 3 ... 4 будут одинаковыми, т. е. для решения задачи необходимо найти усилия N1 и N2.
Решение методом сопромата
Вырежем узел 4 и составим сумму проекций всех сил на вертикальную ось:
Определяя отсюда усилие N2 получим:
Слайд 59Для определения усилий необходимо записать условие совместности деформации стержней, которое
следует непосредственно из рис. а и имеют вид
. Согласно закону Гука , где , , т. e. окончательно получим уравнение совместности дефор-маций в виде:Совместное решение уравнений равновесия и совместности деформаций дает:
Рассматриваемая система один раз статически неопределима:
Смещение точки 4 по вертикали, очевидно, равно удлинению стержня 2 ... 4, т. е.
Слайд 60Решение с использованием принципа наименьшей работы
Исходный функционал
Так как все стержни
работают на растяжение, то все напряжения кроме нормальных продольных равны
нулю. Следовательно дополнительная потенциальная энергия стержня имеет вид:Дополнительная энергия всей системы равна сумме дополнительных энергий стержней
Согласно принципу наименьшей работы из всех статически возможных систем усилий, сводящихся в узле 4 к силе Р, т. е. удовлетворяющих уравнению равновесия, действительные усилия сообщают минимальное значение.
Слайд 61Исключаем из выражения для дополнительной потенциальной энергии N2 с помощью
уравнения равновесия:
записываем условие минимума функции
отсюда
Из уравнения равновесия
Слайд 625.5 Теорема Кастильяно
Будем рассматривать произвольную деформируемую систему, находящуюся под внешним
воздействием, напряженное состояние которой определено и требуется найти смещение некоторой
точки k по направлению, заданному направляющими косинусами lk, mk, nk. Для решения задачи приложим в точке k неизвестную силу Pk по направлению искомого перемещения. Тогда, относя рассматриваемую систему к декартовой системе координат х, у, z, запишем составляющие силы Pk, действующие по осям:Вычисляя работу этой силы на перемещениях иk, vk, wk, имеющих место в точке k, получим:
Записанное в скобках выражение представляет собой интересующее нас перемещение fk, т. е.
Выражение для вариации работы сил будет равно:
Слайд 63Дополнительная потенциальная энергия в рассматриваемом случае будет функцией приложенной силы
Pk и, следовательно, ее вариация примет вид:
Используя принцип Кастильяно в
форме получим равенство:которое в силу произвольности вариации дает:
Полученное равенство формулируется в виде теоремы Кастильяно: частная производная от дополнительной потенциальной анергии по обобщенной силе равна перемещению по направлению этой силы (проекции полного перемещения на направление силы). Под обобщенной силой здесь понимается сила или момент. В последнем случае fk будет представлять собой соответствующий угол поворота.
Слайд 645.6 Пример 2. Стержневая система (продолжение)
Покажем как при помощи теоремы
Кастильяно можно найти перемещение точки 4 стержневой системы показанной на
рисунке. Решение этой задачи методами «Сопротивления материалов» было показано в подвопросе 4.3Запишем как функцию силы P, действующей в этом узле.
Подставляя значение найденных усилий
в выражение для дополнительной потенциальной энергии
получим:
Слайд 665.7 Пример 3. Консольная балка
Рассмотрим пример определения прогиба на конце
консольной балки постоянной жесткости ЕJ, загруженной равномерной поперечной нагрузкой.
Поскольку в
месте искомого прогиба внешней силы Р нет, приложим ее дополнительно (такой же прием использовался при выводе формулы Мора). Тогда изгибающий момент в произвольном сечении х от заданной нагрузки q и введенной силы Р будет равен:Нормальные напряжения выразятся в соответствии с теорией изгиба балок формулой:
Здесь J — момент инерции сечения: у — расстояние по вертикали от центральной главной оси инерции сечения.
Слайд 67Для определения дополнительной потенциальной энергии воспользуемся выражением
Так как работа перерезывающих
сил намного меньше работы изгибающего момента, то учитываем только напряжения,
возникающие от изгиба, т.е. σx. Интегрирование по объему заменяем интегрированием по площади поперечного сечения и длине, получаемПодставляем в полученное выражение полученные ранее зависимости для нормального напряжения σx и изгибающего момента M. Получаем
Слайд 68Интеграл
в полученном выражении есть момент инерции
сечения J.
Интегрируем полученное выражение.
Для нахождения перемещения используем теорему Кастильяно
Полученное значение прогиба соответствует задаче, когда балка кроме распределенной нагрузки на свободном конце нагружена силой P а поскольку в исходной задаче ее нет, то следует положить Р равным нулю. В результате прогиб будет равен:
Использованный при решении задачи прием аналогичен тому, который использовался в «Сопротивлении материалов» при получении формулы Мора
Слайд 696. СМЕШАННЫЙ ВАРИАЦИОННЫЙ ПРИНЦИП
В предыдущих вопросах были рассмотрены принципы возможных
изменений деформированного состояния (принцип Лагранжа) и возможных изменений напряженного состояния
(принципы Кастильяно и наименьшей работы), позволяющие построить энергетическим методом соответственно статические соотношения и уравнения совместности деформаций. Можно построить также функционал, из которого будут вытекать физические соотношения для упругого тела.Для этого используем принцип наименьшей работы. Ввиду того, что этот принцип требует, чтобы варьируемые напряжения удовлетворяли уравнениям равновесия и статическим граничным условиям, воспользуемся известным из вариационного исчисления методом множителей Лагранжа и запишем расширенный функционал:
Здесь u, v и w — множители Лагранжа. Из дальнейшего будет видно, что эти множители являются перемещениями, что и учтено в обозначениях.
Слайд 70Согласно принципу наименьшей работы
.
Отметим, что при этом можно варьировать как множители Лагранжа
(т. е. перемещения), так и напряжения, в связи с чем излагаемый вариационный принцип и назван смешанным. При варьировании u, v и w из функционала вытекают уравнения связей, т. е. уравнения равновесия и статические граничные условия.Осуществим варьирование по функциям напряжений, причем следует иметь в виду, что внешние нагрузки являются заданными, т. е. их вариации равны нулю, а вариации функций напряжений можно считать взаимно независимыми, т. е. соотношения, связывающие функции напряжений, уже учтены в функционале. Проводя операцию варьирования функций напряжений и преобразуя объемный интеграл в функционале F с помощью формулы Остроградского-Гаусса, окончательно получим:
Слайд 71Ввиду того, что вариации напряжений произвольны и независимы, следует:
Сопоставляя эти
равенства с соотношениями Коши и законом Гука, можно заключить, что
они являются обобщенным законом Гука, в котором функции деформаций выражены через перемещения с помощью соотношений Коши. Очевиден также физический смысл множителей Лагранжа и, v, w — они являются перемещениями по осям x, y, z.Таким образом, можно заключить, что равенство является аналитической интерпретацией смешанного вариационного принципа, являющегося вариантом принципа Рейсснера, из которого вытекают соотношения упругости.
Слайд 727. Общие замечания относительно рассмотренных вариационных принципов.
Из рассмотренного следует,
что эти принципы позволяют по существу построить функционалы, из которых
методами вариационного исчисления могут быть получены те или иные группы уравнений теории упругости. Поскольку эти уравнения были выведены в первых вопросах лекции, непосредственно может сложиться впечатление о том, что роль вариационных принципов не столь велика. Однако это далеко не так. Отметим прежде всего, что при расчете сложных, состоящих из большого числа взаимодействующих элементов конструкций непосредственный вывод основных уравнений является часто задачей далеко не элементарной — при проектировании силовых факторов и записи геометрических связей он часто требует достаточно сложных пространственных построений, что может явиться причиной ошибок. В то же время потенциальная энергия, являющаяся суммой энергий отдельных элементов, как правило, записывается достаточно просто, а последующие формальные операции минимизации функционала практически гарантируют от ошибок.Слайд 73Кроме того, введение в функционал системы гипотез, которые всегда принимают
при расчете конструкций, позволяет получить корректную систему уравнений и, что
не менее важно, естественные граничные условия, число и точность которых соответствуют порядку и степени точности вариационных уравнений. Отметим, что неудачные или физически необусловленные гипотезы аппарат минимизации функционала перерабатывает, естественно, так же, как удачные, поэтому, осуществляя формальные операции, не следует упускать из виду их физическое содержание.И, наконец, одна из основных возможностей, которую открывает использование вариационных принципов связана с построением так называемых прямых методов получения приближенных решений, когда интегрирование основной системы уравнений заменяется приближенной минимизацией функционала. Эти методы будут изложены в следующей лекции.