Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СТРУКТУРЫ И АЛГОРИТМЫ ОБРАБОТКИ ДАННЫХ
Содержание
- 1. СТРУКТУРЫ И АЛГОРИТМЫ ОБРАБОТКИ ДАННЫХ
- 2. Формы освоения материалаЛекции Домашние заданияЛабораторные работыКурсовой
- 3. Рейтинг (баллы)Лекции: посещение (+5), ответы
- 4. Материалы в электронном видеCYBER2008 \ TXT \ KURAPOVA posobie.doc - теория Задания на лабы Сортировки Lab1.doc Lab2.doc …
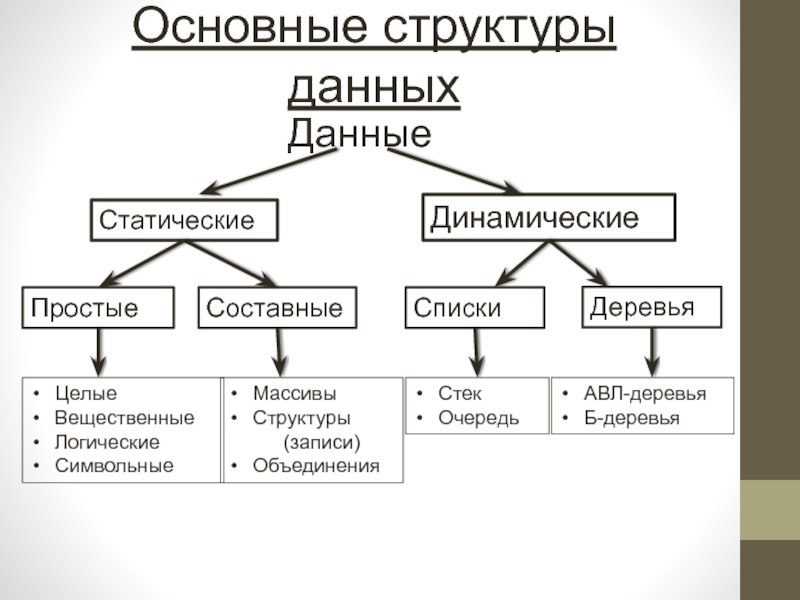
- 5. Основные структуры данныхДанныеСтатическиеДинамическиеПростыеСоставныеСпискиДеревьяЦелыеВещественныеЛогическиеСимвольныеСтекОчередьАВЛ-деревьяБ-деревьяМассивыСтруктуры (записи)Объединения
- 6. Статические данные имеют фиксированную структуру,
- 7. Тип характеризует множество значений, которые может принимать
- 8. Символьный тип определяет полный набор ASCII кода.Перечислимый
- 9. Составные типыСтруктурированные (составные) типы всегда определяют набор
- 10. Тип элементов массива - любой, тип индексов
- 11. Способы доступа к памятиПрямой доступ (случайный) –
- 12. Записи (структуры)Запись состоит из фиксированного числа компонент
- 13. ОбъединенияИспользуются для размещения в одной и той
- 14. Слайд 14
- 15. Псевдокод (некоторые соглашения по записи
- 16. Конструкция ветвления IF (условие)
- 17. Конструкция повтора1. Цикл с предусловиемDO (условие)
- 18. 3. Цикл с параметромDO ( i :=
- 19. СортировкаПричины, по которым мы обращаемся к задаче
- 20. Постановка задачи сортировкиПусть дан массив А =
- 21. Цель сортировки ???– облегчить (ускорить) последующий поиск элементов в отсортированном массиве.
- 22. Слайд 22
- 23. Определение. Серия – это неубывающая последовательность максимальной
- 24. Сортировка элементов со сложной структуройПример: Телефонный справочник
- 25. Таким образом, мы выбрали поля телефонного справочника
- 26. Сортировка рассматривается с точки зрения двух свойств:1. Устойчивость сортировки.2. Зависимость от исходной упорядоченности массива.
- 27. Устойчивость сортировкиОпределение Сортировка называется устойчивой, если после
- 28. Зависимость от исходной упорядоченности массиваЭта характеристика показывает,
- 29. Трудоемкость сортировкиОперации, влияющие на трудоемкость сортировки:1. Сравнение
- 30. При подсчете трудоемкости учитываются только те операции,
- 31. Рассматриваемые алгоритмы написаны на естественном языке, в
- 32. Скачать презентанцию
Формы освоения материалаЛекции Домашние заданияЛабораторные работыКурсовой проектФормы контроля знанийКонтроль посещения лекций (проверка!)Проверка домашних заданий (оценка)Защита лабораторных работ (оценка)Защита курсового проекта (оценка)Экзамен (оценка)Конспект лекций (конкурс!)
Слайды и текст этой презентации
Слайд 1СТРУКТУРЫ И АЛГОРИТМЫ
ОБРАБОТКИ ДАННЫХ
Янченко (Курапова)
Елена Викторовна
Кафедра ПМиК:
430а (гл.корпус),
Слайд 2Формы освоения материала
Лекции
Домашние задания
Лабораторные работы
Курсовой проект
Формы контроля знаний
Контроль
посещения лекций (проверка!)
Проверка домашних заданий (оценка)
Защита лабораторных работ (оценка)
Защита курсового
проекта (оценка)Экзамен (оценка)
Конспект лекций (конкурс!)
Слайд 3Рейтинг (баллы)
Лекции: посещение (+5), ответы (+), пропуск (-5)
Лабораторные
работы: оценки 3, 4, 5, 5+
баллы 3, 5, 7, 10пропуск (-5)
Домашние задания: оценки 3, 4, 5, 5+
баллы 1, 3, 5, 7
Автомат: ≥80% от max, все лабораторные ≥4, ДЗ ≥4, контрольные сроки ≥ 1
Собеседование (полуавтомат):
от 60% до 80% от max, все лабораторные ≥3, ДЗ ≥3, контрольные сроки ≥ 0
Экзамен по билетам: <60% от max с предварительной отработкой лабораторных работ
Слайд 4Материалы в электронном виде
CYBER2008 \ TXT \ KURAPOVA
posobie.doc - теория
Задания
на лабы
Сортировки
Lab1.doc Lab2.doc
…
Слайд 5Основные структуры данных
Данные
Статические
Динамические
Простые
Составные
Списки
Деревья
Целые
Вещественные
Логические
Символьные
Стек
Очередь
АВЛ-деревья
Б-деревья
Массивы
Структуры
(записи)
Объединения
Слайд 6Статические данные имеют фиксированную структуру, поэтому размер
выделенной для них памяти постоянен.
Динамические данные изменяют свою структуру
в процессе работы программы, при этом изменяется объём выделенной памяти.Слайд 7Тип характеризует множество значений, которые может принимать переменная.
Целые типы
различаются количеством байт, отведённых в памяти и наличием знака. (int,
short, long)Вещественные типы характеризуются точностью представления числа. (double, float, long double)
Простые типы данных
Слайд 8Символьный тип определяет полный набор ASCII кода.
Перечислимый тип - перечисление
всех возможных значений.
Логический тип - частный случай перечислимого типа с
двумя возможными значениями ИСТИНА и ЛОЖЬ.Слайд 9Составные типы
Структурированные (составные) типы всегда определяют набор компонентов одинакового или
разного типа.
Массивы – структура данных, которая представляет собой фиксированное
количество элементов одного типа. Слайд 10Тип элементов массива - любой,
тип индексов массива –
только
скалярный.
Массив – это структура данных со случайным (прямым) доступом.
Слайд 11Способы доступа к памяти
Прямой доступ (случайный) – в любой момент
времени доступен любой элемент.
Последовательный доступ – (к+1)-й элемент может быть
получен только путем просмотра предыдущих к элементов.Слайд 12Записи (структуры)
Запись состоит из фиксированного числа компонент называемых полями, которые
могут быть разных типов.
Пример. Struct data { char day;
char month;int year; }
zap[n]; - массив записей.
Поле записи может являться записью, тогда образуются вложенные записи.
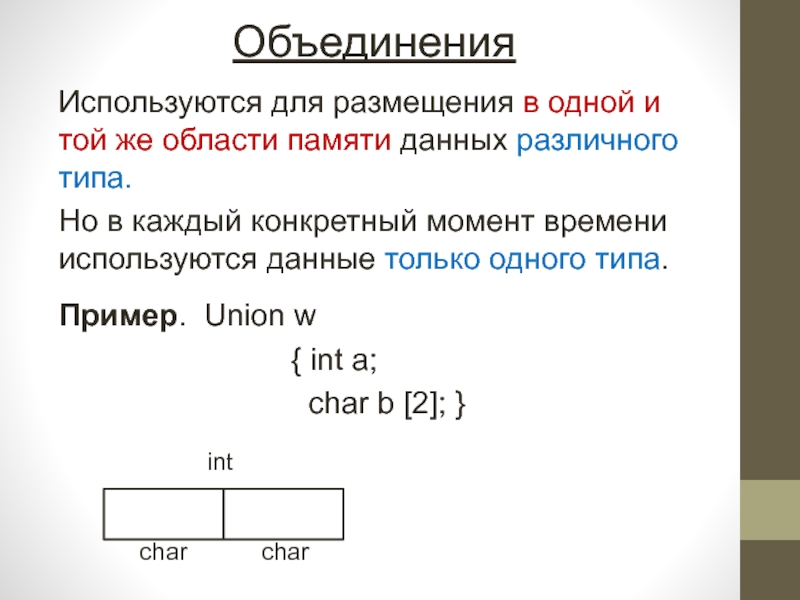
Слайд 13Объединения
Используются для размещения в одной и той же области памяти
данных различного типа.
Но в каждый конкретный момент времени используются
данные только одного типа.Пример. Union w
{ int a;
char b [2]; }
int
char char
Слайд 15Псевдокод
(некоторые соглашения
по записи алгоритмов)
Алгоритм на псевдокоде записывается в
свободной форме на естественном языке
с использованием двух формализованных конструкций:
ветвления и повтора.Слайд 16
Конструкция ветвления
IF (условие)
FI
IF (условие)
ELSE
FI
IF (условие1)
<действие1>ELSE IF (условие2) <действие2>
FI
FI
Слайд 17Конструкция повтора
1. Цикл с предусловием
DO (условие)
OD
2.
Цикл с постусловием
DO
OD (условие)
Слайд 183. Цикл с параметром
DO ( i := 1, 2, …,
n )
OD
4. Бесконечный цикл
DO
<действия> …
IF (условие) OD FI
…
OD
Присваивание :=
Обмен значений
Слайд 19Сортировка
Причины, по которым мы обращаемся к задаче сортировки в нашем
курсе
Сортировка – фундаментальная деятельность, без которой не обходится ни одна
обработка реальных данных.2) На примере сортировки удобно
рассматривать множество алгоритмов,
сравнивать и анализировать их.
Слайд 20Постановка задачи сортировки
Пусть дан массив А = { а1, а2,
…, аn }.
Для всех его элементов определены операции
отношения: меньше, больше, равно (<, >, =).
Необходимо отсортировать массив, т.е.
переставить элементы массива А таким образом,
что выполняется одно из следующих неравенств:
a1 ≤ а2 ≤ а3 ≤ … ≤ аn (1)
a1 ≥ a2 ≥ a3 ≥ ... ≥ an (2)
Если выполняется неравенство (1), то массив отсортирован по возрастанию или в прямом порядке.
Если выполняется неравенство (2), то массив отсортирован по убыванию или в обратном порядке.
Слайд 21Цель сортировки ???
– облегчить (ускорить) последующий поиск элементов в отсортированном
массиве.
Слайд 23Определение. Серия – это неубывающая последовательность максимальной длины.
Пример:
5 6 8 1 3
5 5 4 2 7 65 неубывающих послед-тей => 5 серий
Массив, отсортированный по возрастанию, состоит из одной серии,
а в массиве, отсортированном по убыванию, количество серий равно количеству элементов в массиве (если все элементы различны).
Слайд 24Сортировка элементов со сложной структурой
Пример: Телефонный справочник –
сложная структура,
состоит из:
Фамилии; Имени; Телефона; Адреса.
Чтобы его отсортировать, нужно определить
отношения порядка (<,>,=).Например, пусть при сравнении двух элементов меньше тот, чья фамилия идет раньше по алфавиту.
Если фамилии совпадают, то меньше элемент, у которого имя раньше по алфавиту.
Если фамилии и имена совпадают, то будем считать, что элементы равны.
Слайд 25Таким образом, мы выбрали поля телефонного справочника для определения отношения
порядка (,=).
Определение. Та часть информации, которая учитывается при определении
отношения порядка, называется ключом сортировки. В данном примере ключ сортировки: фамилия и имя - составной ключ из двух полей (фамилия – старшая часть ключа, имя – младшая часть ключа).
Ключ поиска обычно
-равен ключу сортировки или
-состоит из его старшей части.
Слайд 26Сортировка рассматривается с точки зрения двух свойств:
1. Устойчивость сортировки.
2. Зависимость
от исходной упорядоченности массива.
Слайд 27Устойчивость сортировки
Определение Сортировка называется устойчивой, если после её проведения в
массиве не меняется относительный порядок элементов с одинаковыми ключами.
Пример:
1
2 5’ 6 3 4 5”Итог сортировки:
1 2 3 4 5’ 5” 6 - устойчивая сортировка
1 2 3 4 5” 5’ 6 - неустойчивая сортировка
В общем случае устойчивая сортировка лучше, чем неустойчивая. В частности, когда данные уже были ранее упорядочены по другим ключам.
Слайд 28Зависимость от исходной упорядоченности массива
Эта характеристика показывает, изменяется ли трудоемкость
сортировки в зависимости от исходных данных.
Но все же…
Главным качественным
показателем сортировки является быстрота работы (трудоемкость).Для сравнения методов сортировки необходимо оценивать их эффективность по времени.
Слайд 29Трудоемкость сортировки
Операции, влияющие на трудоемкость сортировки:
1. Сравнение элементов - C
(“Compare”);
2. Перестановки элементов – M (“Move”).
Мы будем оценивать трудоемкость количеством
операций сравнения и перестановки: С + M = T
C и M зависят от количества элементов в массиве:
C(n) + M(n) = T(n),
где C(n), M(n), T(n) – функции от количества элементов массива.
Слайд 30При подсчете трудоемкости учитываются
только те операции, в которых участвуют
элементы массива.
Предварительно обнулить счетчики C=0; M=0;
При подсчете количества сравнений счетчик
желательно ставить перед условным оператором.Пример: С++; if (ai < x) …
При подсчете количества пересылок счетчик ставится до или после оператора присваивания:
Пример: ai=x; M++;
Слайд 31Рассматриваемые алгоритмы написаны на естественном языке, в котором массив нумеруется
от 1 до n: А = { а1 , а2
, …, аn }.Для удобства реализации алгоритмов на языке C++, массив возможно описывать следующим образом:
int A [ 1+n ];
Тогда при заполнении, обработке и выводе массива элемент А[0] не используется.
A[0] A[1] A[2] ... A[n]