Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Структуры и алгоритмы обработки данных
Содержание
- 1. Структуры и алгоритмы обработки данных
- 2. Сортировка 4 2Нижняя граница задачи сортировкиВопрос: существует ли
- 3. Сортировка 4 3Сортировка с минимальным числом сравненийДеревья решений
- 4. Сортировка 4 4Сортировка с минимальным числом сравненийДеревья решений
- 5. Сортировка 4 5Деревья решений (сравнений)b → d
- 6. Сортировка 4 6Деревья решений (сравнений)Пусть m высота дерева
- 7. Сортировка 4 7Формула Стирлинга⎡log2 n!⎤ ≤ log2 n!
- 8. Сортировка 4 8Оптимальная сортировкаБинарные вставки: Пусть S(n) –
- 9. Сортировка 4 9Оптимальная сортировкаS(5) = 7 ?k1, k2,
- 10. Сортировка 4 10Оптимальная сортировка4 и 5-е сравнения: e среди a
- 11. Сортировка 4 11Поразрядная сортировка (Распределяющая сортировка)Пример 1 (с
- 12. Сортировка 4 12Поразрядная сортировка Сортировка колоды карт в
- 13. Сортировка 4 13Поразрядная сортировка В итоге получим 4
- 14. Сортировка 4 14Поразрядная сортировка Пример 2 (с числами).Рассмотрим
- 15. Сортировка 4 15Поразрядная сортировка 203, 045, 141, 405,
- 16. Сортировка 4 16Поразрядная сортировка 130, 141, 321, 522,
- 17. Сортировка 4 17Поразрядная сортировка 203, 405, 513, 321,
- 18. Сортировка 4 18Алгоритм поразрядной сортировкиВ общем случае даны
- 19. Сортировка 4 19Алгоритм поразрядной сортировкиДля представления «ящиков» и
- 20. Сортировка 4 20Алгоритм поразрядной сортировкиАлгоритм: Create(Q); Create(q[*]); for j := 1 to p
- 21. Сортировка 4 21Алгоритм поразрядной сортировкиПодсчитаем количество операций. Внешний
- 22. КОНЕЦ ЛЕКЦИИ
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Структуры и алгоритмы обработки данных, 2
Лекция 5
Сортировка (продолжение)
Нижняя граница задачи
сортировки
Слайд 2Сортировка 4 2
Нижняя граница задачи сортировки
Вопрос: существует ли алгоритм сортировки, основанный
на сравнениях и решающий задачу за меньшее число операций,
чем
O (n log n) при любых входных данных? Сортировка с минимальным числом сравнений
(избыточные сравнения не выполняются)
Деревья решений (сравнений)
Для простоты – все ключи различны.
Основная операция сравнения: ki < kj
Слайд 3Сортировка 4 3
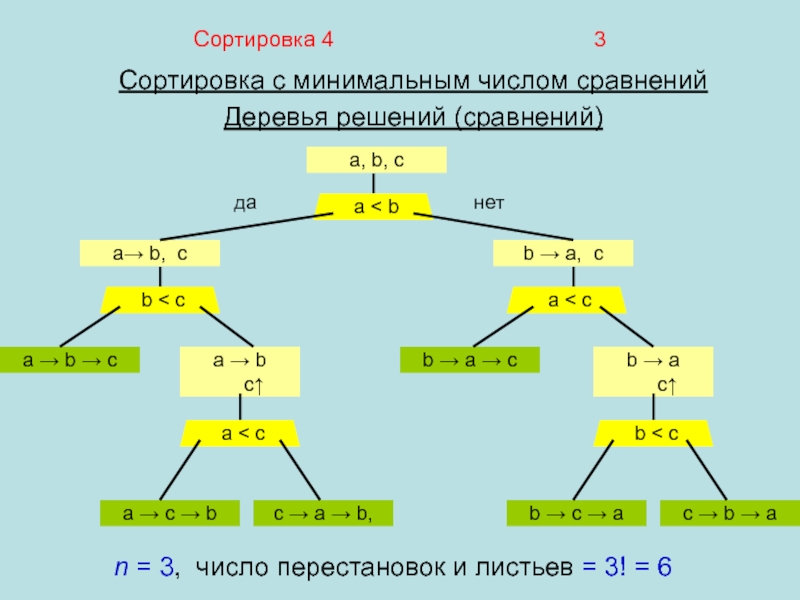
Сортировка с минимальным числом сравнений
Деревья решений (сравнений)
a, b, c
a→
b, c
b → a, c
a → c → b
a
→ b → cb → a → c
a → b
c↑
c → a → b,
b → a
c↑
b → c → a
c → b → a
n = 3, число перестановок и листьев = 3! = 6
да
нет
Слайд 4Сортировка 4 4
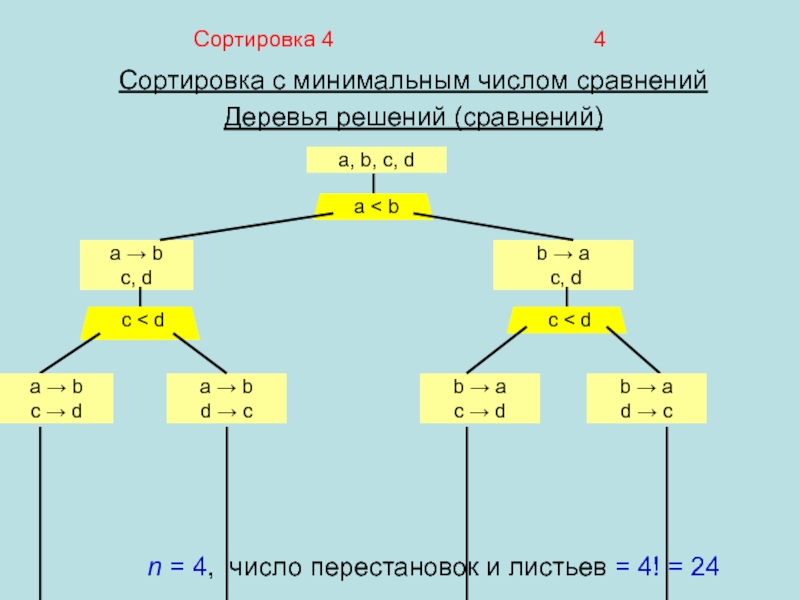
Сортировка с минимальным числом сравнений
Деревья решений (сравнений)
a, b, c,
d
a → b
c, d
b → a
c, d
a →
bd → c
b → a
c → d
n = 4, число перестановок и листьев = 4! = 24
a → b
c → d
b → a
d → c
Слайд 5Сортировка 4 5
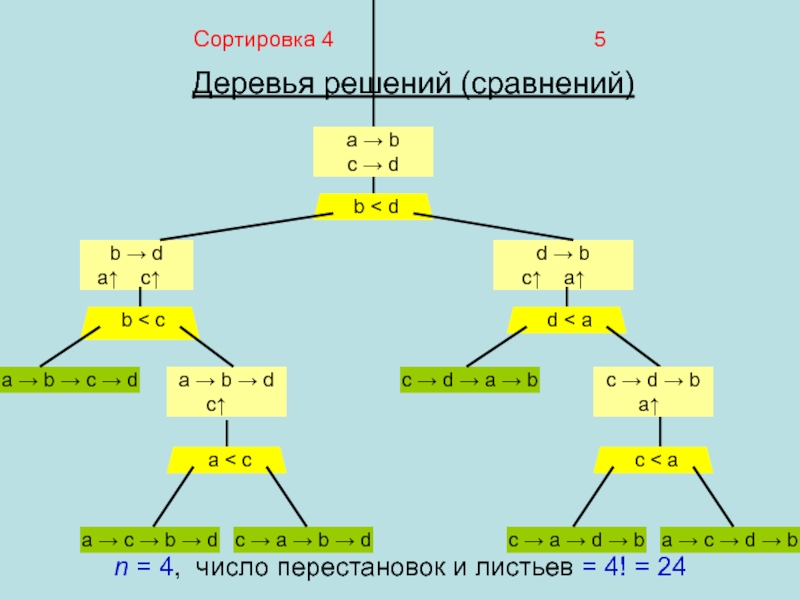
Деревья решений (сравнений)
b → d
a↑ c↑
d
→ b
c↑ a↑
a → c →
b → d a → b → c → d
c → d → a → b
a → b → d
c↑
c → a → b → d
c → a → d → b
a → c → d → b
n = 4, число перестановок и листьев = 4! = 24
c → d → b
a↑
a → b
c → d
Слайд 6Сортировка 4 6
Деревья решений (сравнений)
Пусть m высота дерева (максимальное число сравнений).
2m
≥ число листьев ≥ n!
(число листьев должно быть не
менее числа исходов)m ≥ ⎡log2 n!⎤
Итак, утверждение:
Для любого алгоритма сортировки, основанного на сравнениях, всегда можно подобрать такие исходные данные, что применение алгоритма потребует не менее ⎡log2 n!⎤ шагов.
Слайд 7Сортировка 4 7
Формула Стирлинга
⎡log2 n!⎤ ≤ log2 n! + 1
⎡log2 n!⎤
= n log2 n – n log2 e + (1/2)
log2 n + O(1)Итак, сложность задачи сортировки есть Ω (n log2 n),
а алгоритмы быстрой сортировки и пирамидальной сортировки решают задачу за время Θ (n log2 n)
Слайд 8Сортировка 4 8
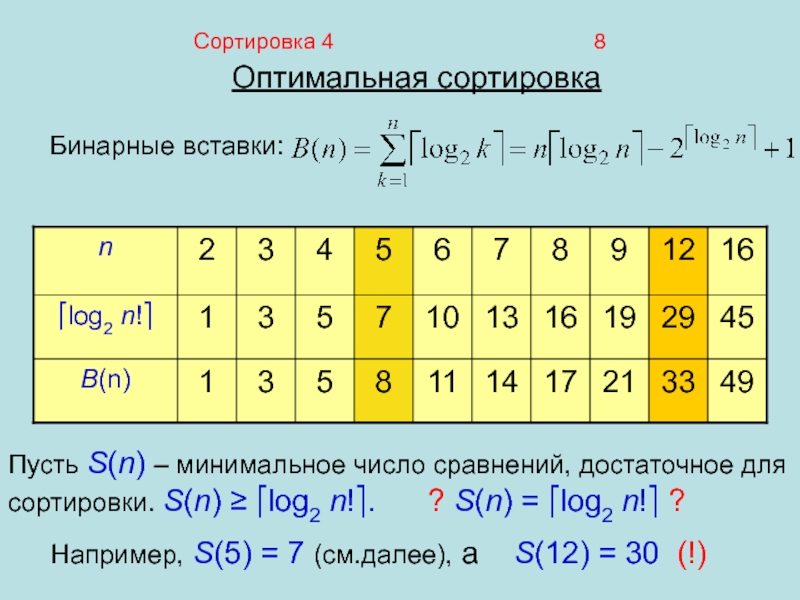
Оптимальная сортировка
Бинарные вставки:
Пусть S(n) – минимальное число сравнений,
достаточное для сортировки. S(n) ≥ ⎡log2 n!⎤. ?
S(n) = ⎡log2 n!⎤ ?Например, S(5) = 7 (см.далее), а S(12) = 30 (!)
Слайд 9Сортировка 4 9
Оптимальная сортировка
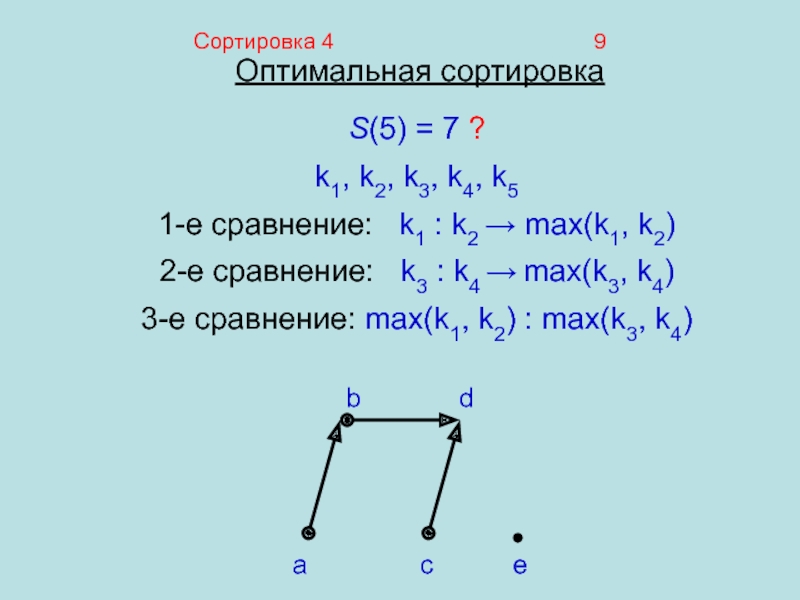
S(5) = 7 ?
k1, k2, k3, k4, k5
1-е сравнение: k1 : k2 → max(k1, k2)
2-е сравнение:
k3 : k4 → max(k3, k4)3-е сравнение: max(k1, k2) : max(k3, k4)
e
b
d
c
a
Слайд 10
Сортировка 4 10
Оптимальная сортировка
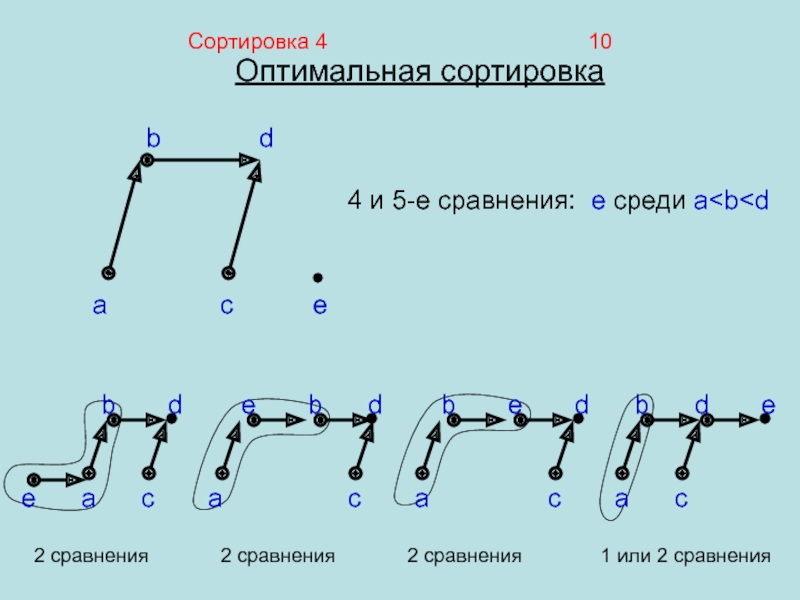
4 и 5-е сравнения: e среди a
сравнения
2 сравнения
1 или 2 сравнения
Слайд 11Сортировка 4 11
Поразрядная сортировка
(Распределяющая сортировка)
Пример 1 (с картами).
Карта = (масть,
достоинство)
Масть: ♣ ‑ трефа, ♦ ‑ бубна, ♥ ‑ черва,
♠ ‑ пикаДостоинство: 2, 3, 4, 5, 6, 7, 8, 9, 10, В, Д, К, Т
Порядок по масти: ♣ < ♦ < ♥ < ♠.
Порядок по достоинству: 2<3<4<5<6<7<8<9<10<В<Д<К<Т
Порядок карт лексикографический:
♣2<♣3<♣4<♣5<♣6<♣7<♣8<♣9<♣10<♣В<♣Д<♣К<♣Т<
♦2<♦3<♦4<♦5<♦6<♦7<♦8<♦9<♦10<♦В<♦Д<♦К<♦Т<
♥2<♥3<♥4<♥5<♥6<♥7<♥8<♥9<♥10<♥В<♥Д<♥К<♥Т<
♠2<♠3<♠4<♠5<♠6<♠7<♠8<♠9<♠10<♠В<♠Д<♠К<♠Т
Слайд 12Сортировка 4 12
Поразрядная сортировка
Сортировка колоды карт в лексикографическом порядке:
1 шаг
– распределяем по достоинству (раскладываем) на кучки («лицом» вверх)
2
В
3
Д
К
Т
4
5
6
7
8
9
10
Затем складываем
кучки друг на друга(последовательно кучки большего достоинства сверху).
2 шаг – держим колоду рубашкой вниз и распределяем
на кучки по масти (карты кладем лицом вверх).
При этом в каждой «кучке по масти» карты лягут в порядке возрастания достоинства вниз кучки.
Слайд 13Сортировка 4 13
Поразрядная сортировка
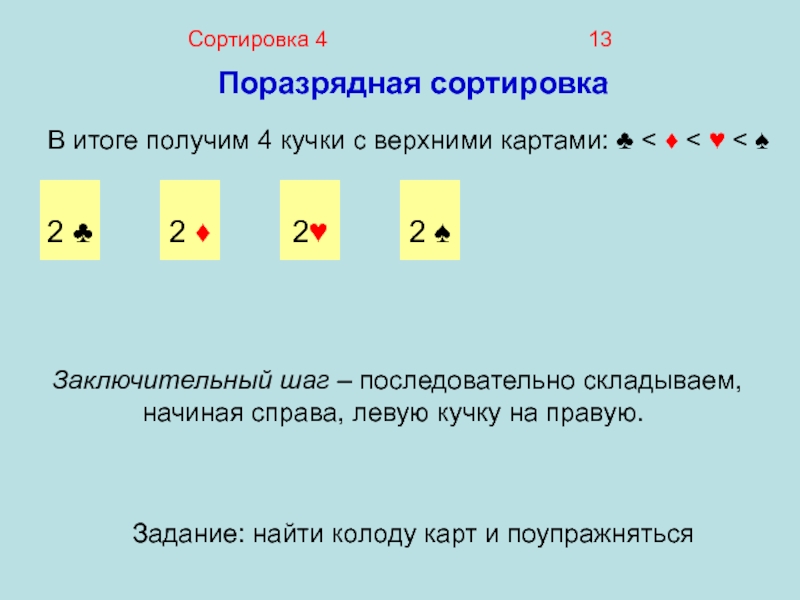
В итоге получим 4 кучки с верхними
картами: ♣ < ♦ < ♥ < ♠
2 ♣
2 ♦
2
♠
2♥
Заключительный шаг – последовательно складываем, начиная справа, левую кучку на правую.
Задание: найти колоду карт и поупражняться
Слайд 14Сортировка 4 14
Поразрядная сортировка
Пример 2 (с числами).
Рассмотрим целые (положительные) трехразрядные
числа
в позиционной шестиричной системе счисления,
т.е. каждый разряд содержит цифры
0, 1, 2, 3, 4, 5Например, пусть дана последовательность из 9 чисел
203, 045, 141, 405, 321, 522, 130, 054, 513
1 шаг – распределяем числа последовательности сначала по младшей цифре по ящикам с «именами»: «0», «1», «2», «3», «4», «5».
Ящики заполняются снизу вверх.
Слайд 15Сортировка 4 15
Поразрядная сортировка
203, 045, 141, 405, 321, 522, 130,
054, 513
Сцепляем последовательно слева направо содержимое ящиков в одну последовательность,
так, что нижнее число правого ящика следует за верхним числом левого соседнего ящика (внутри ящиков последовательность расположена снизу вверх). Таким образом, получим последовательность130, 141, 321, 522, 203, 513, 054, 045, 405.
Заметим, что младшие цифры этой последовательности упорядочены по неубыванию.
Слайд 16Сортировка 4 16
Поразрядная сортировка
130, 141, 321, 522, 203, 513, 054,
045, 405
2 шаг – аналогичным образом распределяем по ящикам числа
полученной последовательности по средней цифре.Повторяя сцепление содержимого ящиков, получим последовательность
203, 405, 513, 321, 522, 130, 141, 045, 054,
упорядоченную по двум младшим цифрам.
Слайд 17Сортировка 4 17
Поразрядная сортировка
203, 405, 513, 321, 522, 130, 141,
045, 054
3 шаг – аналогичным образом распределяем по ящикам числа
полученной последовательности по старшей цифре.Повторяя сцепление содержимого ящиков, получим упорядоченную последовательность
045, 054, 130, 141, 203, 321, 405, 513, 522.
Слайд 18Сортировка 4 18
Алгоритм поразрядной сортировки
В общем случае даны числа (ключи):
x1,
x2, x3,…, xn.
Каждый ключ состоит из p разрядов:
( ∀ i ∈1..n: xi = (xi(p), xi(p−1),…, xi(1))
), а каждый q-й разряд представлен цифрой xi(q) ∈0..r−1.
Тогда
(xi < xj) ↔
(∃ t ∈1..p: (∀ q ∈ t + 1..p: xi(q) = xj(q)) & (xi(t) < xj(t))).
Слайд 19Сортировка 4 19
Алгоритм поразрядной сортировки
Для представления «ящиков» и их сцепления в
новую последовательность используем очереди:
Q – общая очередь (исходная, промежуточные и
результирующая последовательности);q[0], q[1],…, q[r − 1] – очереди по каждой r-ичной цифре («ящики»).
Слайд 20Сортировка 4 20
Алгоритм поразрядной сортировки
Алгоритм:
Create(Q); Create(q[*]);
for j := 1 to p do
for k := 0 to r − 1 do
Empty(q[k]) od;
while not Null(Q) do
x ← Q;
Пусть x = (x(p), x(p−1),…, x(1)), тогда
q[x(j)] ← x
od {while};
Q ← сцепление(q[0], q[1],…, q[r − 1])
od {for
j}Слайд 21Сортировка 4 21
Алгоритм поразрядной сортировки
Подсчитаем количество операций.
Внешний цикл по разрядам
выполняется p раз.
Каждая итерация этого цикла для каждого из
n чисел выполняет извлечение и запись в очередь, т.е. всего 2n таких операций. Кроме того, на каждой итерации происходит r − 1 сцепление очередей.
Таким образом на одной итерации требуется 2n + r − 1 операций,
а всего по всем разрядам O (p n + p r ) операций.
Сравнение с O ( n log n ) !...












![Структуры и алгоритмы обработки данных Сортировка 4 20Алгоритм поразрядной сортировкиАлгоритм: Create(Q); Create(q[*]); for j := 1 to p do for k := 0 to r − 1 do Empty(q[k]) Сортировка 4 20Алгоритм поразрядной сортировкиАлгоритм: Create(Q); Create(q[*]); for j := 1 to p do for k := 0 to r − 1 do Empty(q[k]) od; while not Null(Q) do x ← Q; Пусть x = (x(p), x(p−1),…, x(1)), тогда q[x(j)] ← x od {while}; Q ← сцепление(q[0],](/img/thumbs/91b4a5fb89d67b7f9503a9249ba74abf-800x.jpg)





















