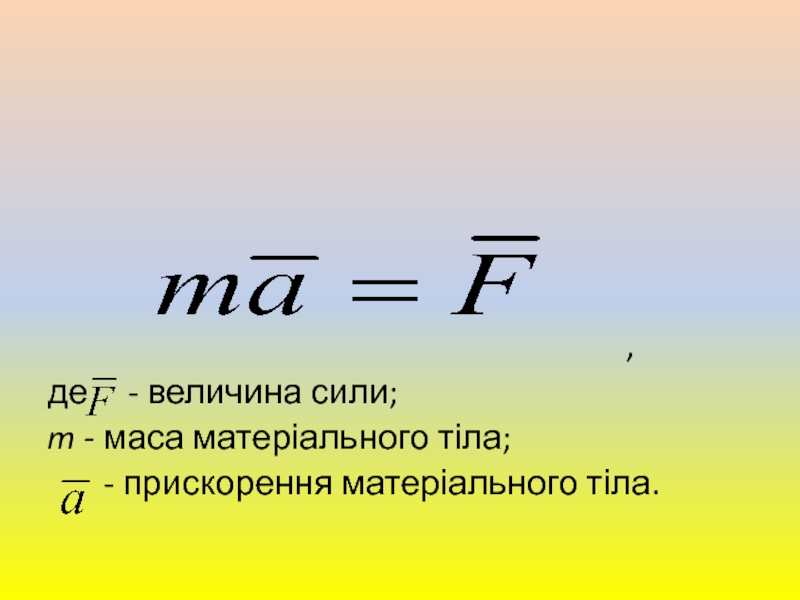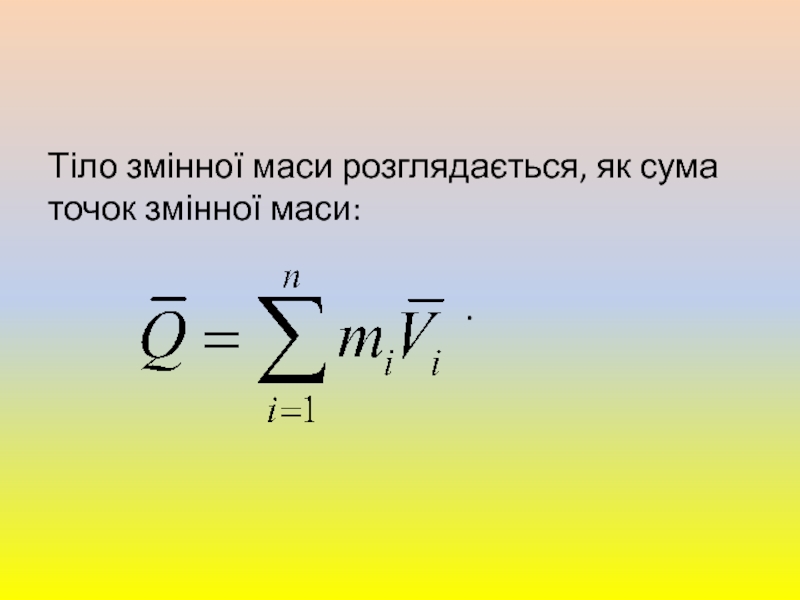Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сумський державний університет Кафедра військової підготовки
Содержание
- 1. Сумський державний університет Кафедра військової підготовки
- 2. Навчальні питанняРівняння поступального та обертального руху тіл змінної маси.Фізична сутність та формула сили тяги.
- 3. Перше питанняРівняння поступального та обертального руху тіл змінної маси.
- 4. Основні закони механіки польоту ЛА. Основні
- 5. Найпростішим тілом, що рухається, вважають матеріальну точку.
- 6. Механічний рух твердого тіла можна спостерігати та
- 7. При вивченні руху ЛА відносно Землі будемо
- 8. Центром мас (ЦМ) системи матеріальних точок називають
- 9. Просторова лінія, яку описує будь-яка точка тіла,
- 10. Рух вважається прямолінійним, якщо його траєкторія є
- 11. ьРух одного і того ж тіла відносно
- 12. Якщо рух тіла розглядається відносно нерухомих предметів
- 13. Тверде тіло може здійснювати простий рух чи
- 14. Поступальним називається такий рух тіла, коли всі
- 15. Обертальний рух відбувається навколо нерухомої осі і
- 16. Число незалежних параметрів, при завданні яких однозначно
- 17. Матеріальне тіло, на яке не накладені зв'язки
- 18. Як вже відмічалося, рух тіла відносно нерухомої
- 19. Рух рухомої системи відліку відносно нерухомої називають
- 20. Швидкість абсолютного руху є геометричною сумою швидкостей відносного і переносного рухів, тобто
- 21. Прийнято вважати рух тіла відомим чи заданим,
- 22. Основні закони класичної механіки Перший
- 23. Властивість матеріального тіла зберігати рівномірний і прямолінійний
- 24. Другий закон Ньютона (встановлює зв'язок між силою
- 25. Слайд 25
- 26. Третій закон Ньютона (закон рівності дії і
- 27. Рівняння руху тіл змінної масиРакету, за рахунок
- 28. Загальна теорія руху ракет використовує основні поняття
- 29. Кількістю руху матеріальної точки змінної маси називають
- 30. Тіло змінної маси розглядається, як сума точок
- 31. Моментом кількості руху чи кінетичним моментом називають
- 32. Кінетичний момент тіла змінної маси визначається відповідно:
- 33. Використовуючи поняття про зміну кількості руху тіла
- 34. Перейдемо до другого рівняння, яке характеризує обертовий
- 35. Умовно розділімо маховик на n елементарних матеріальних
- 36. Кінетичний момент для матеріальної частки масою
- 37. Для кінетичного моменту тіла відносно вісі обертання
- 38. Після математичних перетворень основним рівнянням обертального руху
- 39. Слайд 39
- 40. Скачать презентанцию
Навчальні питанняРівняння поступального та обертального руху тіл змінної маси.Фізична сутність та формула сили тяги.
Слайды и текст этой презентации
Слайд 1Сумський державний університет
Кафедра військової підготовки
Групове заняття з предмету
«Конструкція ракет»
Тема
1 - Загальна характеристика ракет
в загальному вигляді.
Слайд 2Навчальні питання
Рівняння поступального та обертального руху тіл змінної маси.
Фізична сутність
та формула сили тяги.
Слайд 4Основні закони механіки польоту ЛА. Основні відомості щодо руху твердого
тіла
Під механічним рухом розуміють зміну з часом положення матеріальних тіл
відносно один одного. Ця зміна характеризується зміною відстані між матеріальними тілами.
Слайд 5Найпростішим тілом, що рухається, вважають матеріальну точку. Тобто таке тіло,
розмірами якого при вивченні його руху можна знехтувати. Будь-яке тверде
тіло можна представити у вигляді системи, яка складається із жорстко зв'язаних матеріальних точок. У механіці, як правило, розглядають рух абсолютно твердого тіла, під яким розуміють тіло, відстань між частицями якого за всіх умов залишається незмінною.
Слайд 6Механічний рух твердого тіла можна спостерігати та вивчати тільки стосовно
будь-яких інших тіл.
Система координат, яка зв'язана з тілом, відносно якого
розглядається даний рух, називається системою відліку.
Слайд 7При вивченні руху ЛА відносно Землі будемо вважати ЛА матеріальною
точкою (виходячи з того, що розміри траєкторії польоту ЛА значно
більші за її розміри), як правило ця точка співпадає з центром мас ЛА.
Слайд 8Центром мас (ЦМ) системи матеріальних точок називають таку точку, в
якій зібралася б уся маса системи матеріальних точок, якби вони
взаємодіяли з нескінченно зростаючими силами притягання.
Слайд 9Просторова лінія, яку описує будь-яка точка тіла, наприклад, ЦМ під
час руху, називається траєкторією точки. За видом траєкторії відрізняють прямолінійний
і криволінійний рух.
Слайд 10Рух вважається прямолінійним, якщо його траєкторія є прямою лінією, і
криволінійним, коли траєкторія - крива лінія, що свідчить про непостійний
напрямок руху.
Слайд 11ь
Рух одного і того ж тіла відносно різних систем відліку
може бути різним. Поняття рух і спокій відносні і мають
сенс тільки при визначенні системи відліку, стосовно якої вони розглядаються. Наприклад, пасажир, який сидить у вагоні потягу, що рухається рівномірно і прямолінійно, відносно вагону знаходиться у стані спокою, тоді як стосовно Землі здійснює рух разом з вагоном.
Слайд 12Якщо рух тіла розглядається відносно нерухомих предметів і тіл (відносно
нерухомої системи відліку), він називається абсолютним. Рух тіла називають відносним,
якщо оточуючі його предмети рухаються.
Слайд 13Тверде тіло може здійснювати простий рух чи брати участь у
складному русі. Найпростішими видами руху твердого тіла вважають його поступальний
та обертальний рух.
Слайд 14Поступальним називається такий рух тіла, коли всі його точки рухаються
по однакових і паралельно розташованих траєкторіях, при цьому будь-яка пряма,
проведена між двома точками тіла, не змінює свого напрямку і залишається паралельною сама собі за весь час руху. Внаслідок того, що всі точки твердого тіла рухаються по однаковим траєкторіям, переміщення усіх точок тіла геометрично рівні між собою. Прикладом поступального руху є рух ЛА відносно Землі при незмінному її кутовому положенні.
Слайд 15Обертальний рух відбувається навколо нерухомої осі і є таким рухом,
при якому кожна точка тіла знаходиться на незмінній відстані від
осі обертання.Тверде тіло в загальному випадку може здійснювати складний рух, тобто одночасно брати участь у декількох поступальних і обертальних переміщеннях.
Слайд 16Число незалежних параметрів, при завданні яких однозначно визначається вид руху
і положення твердого тіла в просторі, називається числом ступенів свободи.
Слайд 17Матеріальне тіло, на яке не накладені зв'язки з боку інших
тіл, називають вільним. Вважають, що вільне тіло має шість ступенів
свободи. Це означає, що вільне тіло може здійснювати шість різних рухів: рухатись поступально відносно трьох взаємно перпендикулярних осей (три ступені поступального руху) і обертатися навколо кожної з цих осей (три ступені обертального руху). Прикладом вільного тіла є літак чи ракета в польоті.
Слайд 18Як вже відмічалося, рух тіла відносно нерухомої системи приймають за
абсолютний рух. Часто на практиці буває зручно абсолютний рух розглядати
як складний рух, який складається з двох одночасних рухів: рух тіла відносно деякої рухомої системи (наприклад, відносно зв'язаної системи координат) і руху тіла сумісно з рухомою системою відліку відносно нерухомої.Відносно рухомої системи координат рух тіла називають відносним рухом. Він характеризується швидкістю відносного руху .
Слайд 19Рух рухомої системи відліку відносно нерухомої називають переносним рухом і
характеризують його швидкістю переносного руху .
Слайд 20Швидкість абсолютного руху є геометричною сумою швидкостей відносного і переносного
рухів, тобто
Слайд 21Прийнято вважати рух тіла відомим чи заданим, якщо в будь-який
момент часу можна визначити напрям руху тіла та його положення
відносно вибраної системи координат.
Слайд 22
Основні закони класичної механіки
Перший закон Ньютона (закон інерції): будь-яке матеріальне
тіло зберігає стан спокою чи рівномірного прямолінійного руху до тих
пір, поки вплив з боку інших тіл не змінить його стану.
Слайд 23Властивість матеріального тіла зберігати рівномірний і прямолінійний рух, чи знаходитись
у стані спокою при відсутності дії на нього сил, називається
інерцією.
Слайд 24Другий закон Ньютона (встановлює зв'язок між силою і прискоренням): сила,
що діє на матеріальне тіло, надає йому прискорення, пропорційне величині
сили та направлене у той самий бік, що і ця сила.
Слайд 26Третій закон Ньютона (закон рівності дії і протидії): будь -
якої дії завжди відповідає рівна за величиною і протилежно направлена
протидія.
Слайд 27Рівняння руху тіл змінної маси
Ракету, за рахунок палива яке витрачається
під час польоту, приймають як тіло змінної маси. Вперше рівняння
руху тіл змінної маси було виведено у 1897 р. І.В.Мещерським і названо його іменем. Із теоретичної механіки відомо, що характеристики руху твердого тіла можуть бути визначені із розглядання поступального руху ЦМ тіла і обертового руху відносно ЦМ.
Слайд 28Загальна теорія руху ракет використовує основні поняття механіки точки змінної
маси: зміну кількості руху і зміну кінетичного моменту.
Слайд 29Кількістю руху матеріальної точки змінної маси називають вектор
,
де m – змінна маса точки;
- вектор швидкості точки.
Слайд 31Моментом кількості руху чи кінетичним моментом називають вектор:
де
- радіус-вектор точки змінної маси, проведений із початку деякої нерухомої
системи координат до точки, яка рухається.
Слайд 33Використовуючи поняття про зміну кількості руху тіла змінної маси, отримують
рівняння поступального руху ЦМ ракети.
Розуміння його складається у наступному:
для любого моменту часу при польоті ракети (тіла змінної маси) добуток маси ракети на її прискорення дорівнює геометричній сумі рівнодіючих всіх зовнішніх сил і додаткової сили тяги .
Слайд 34Перейдемо до другого рівняння, яке характеризує обертовий рух ракети відносно
ЦМ. Ми вже визначали, що обертовий рух відносно ЦМ ракети
характеризує кінетичний момент:
Слайд 35Умовно розділімо маховик на n елементарних матеріальних часток з масою
і розглянемо одну з часток
, яка знаходиться на відстані від вісі обертання. Так як обертання відбувається з кутовою швидкістю , то частка буде мати лінійну швидкість , яка має напрямок, що перпендикулярний радіусу .
Слайд 36Кінетичний момент для матеріальної частки масою
відносно вісі обертання розраховується по формулі:
Визначимо лінійну швидкість
через кутову швидкість :
Слайд 37Для кінетичного моменту тіла відносно вісі обертання маємо:
де
- момент
інерції тіла відносноосі
Слайд 38Після математичних перетворень основним рівнянням обертального руху є:
Якщо порівняти рівняння
з основним законом поступального руху , можливо зробити висновок, що при обертанні тіла навколо вісі момент сили грає таку ж роль, що і сила при поступальному руху, а момент інерції тіла І– як маса m , тобто визначає опір тіла при його обертанні впливу зовнішніх сил.
