Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Суждение
Содержание
- 1. Суждение
- 2. Что является суждением?Всякое суждение выражается с помощью
- 3. ИсключенияЕсть, однако, вопросительно-риторические предложения, их еще называют
- 4. Основные определенияСуждение – это мысль, в которой
- 5. Логика классическая и неклассическаяЕсли мы исходим из
- 6. Суждения простые и сложныеПростым суждением называется суждение,
- 7. Типичное простое суждениеСуждение, в котором выражена связь
- 8. Виды простых сужденийВ традиционной логике установилось деление
- 9. Атрибутивные сужденияЛогическая структура: S есть (не есть)
- 10. Суждения с отношениямиЛогическая структура: R
- 11. Суждения существованияЛогическая форма суждения существования может быть
- 12. Доказательство бытия БогаБог, по определению, является максимально
- 13. Категорические сужденияАтрибутивные суждения, определенные по количеству и
- 14. Объединенная классификацияОбщеутвердительные суждения. Стандартная форма: «Все S
- 15. Сокращенные наименованияНазвания суждений громоздкие, произносятся не без
- 16. Выделяющие сужденияОбщие, частные и единичные суждения могут
- 17. Исключающие сужденияПо количеству, суждения могут быть исключающими.
- 18. Распределенность терминов в категорических суждениях Термины
- 19. Суждения типа АВ общеутвердительном суждении S распределен
- 20. Схема распределенности терминов в суждениях типа А
- 21. Суждение I (Некоторые S есть Р).«Некоторые студенты
- 22. Круговая схема I
- 23. Суждение Е (Ни одно S не есть
- 24. Круговая схема Е
- 25. Суждение О (Некоторые S не есть Р)«Некоторые
- 26. Круговая схема О
- 27. Обобщенная таблица
- 28. Логический квадрат
- 29. Отношения по логическому квадратуОтношение между А и
- 30. Противоположность2. Суждения А и Е находятся в
- 31. Противность3. Суждения I и О находятся в
- 32. Противоречие4. Суждения А и О, а также
- 33. Скачать презентанцию
Что является суждением?Всякое суждение выражается с помощью грамматического предложения. Главной характеристикой суждения является его способность описывать ситуацию в действительности, соответствовать или не соответствовать этой ситуации, т.е. быть истинным или ложным.Не всякое
Слайды и текст этой презентации
Слайд 1Суждение
Суждение; суждение и предложение; принцип двузначности; простые суждения; отношения между
суждениями
Слайд 2Что является суждением?
Всякое суждение выражается с помощью грамматического предложения.
Главной
характеристикой суждения является его способность описывать ситуацию в действительности, соответствовать
или не соответствовать этой ситуации, т.е. быть истинным или ложным.Не всякое предложение является суждением.
Суждениями не являются вопросы, побудительные, восклицательные предложения. Почему?
Слайд 3Исключения
Есть, однако, вопросительно-риторические предложения, их еще называют «риторический вопрос». Они
выражают суждения, поскольку в них можно обнаружить истинность или ложность,
их также можно охарактеризовать как утвердительные или отрицательные. В риторическом вопросе «Кто же этого не знает?» утверждается, что «Это знают все».Слайд 4Основные определения
Суждение – это мысль, в которой утверждается или отрицается
наличие связей между предметами и их свойствами, а также отношений
между предметами.В классической логике каждое суждение рассматривается либо как истинное, либо как ложное. Это положение получило название принципа двузначности.
Слайд 5Логика классическая и неклассическая
Если мы исходим из двух значений истинности
– суждение истинное или ложное, то логика является двузначной.
Но
может быть и третье значение истинности – суждение неопределенное. В основном это относится к суждениям, в которых выражены сведения о будущих событиях или происходящих на далеких расстояниях. Например, «К концу года инфляция составит десять процентов». Или «На Марсе существует разумная жизнь». При трех значениях истинности – суждение истинное, или ложное, или неопределенное – логику называют трехзначной. Есть еще и многозначные логики. В традиционной логике, за небольшими исключениями, рассматриваются два значение истинности – истинное суждение или ложное.
Слайд 6Суждения простые и сложные
Простым суждением называется суждение, которое не содержит
в себе других суждений в качестве логической части.
Сложным суждением
называется суждение, содержащее в себе другие суждения в качестве логической частиСлайд 7Типичное простое суждение
Суждение, в котором выражена связь предмета и его
признака, включает два термина суждения (два понятия).
Субъект суждения –
это часть суждения, которая отображает предмет мысли, то, о чем говорится в суждении. Субъект (от латинского subjectum – лежащий в основе) обозначается большой буквой S. Второй термин предикат – то, что говориться о субъекте, признак предмета. Предикат (от латинского praedicatum – сказанное) обозначается большой буквой P.
Для соединения терминов, субъекта и предиката, имеется третий элемент суждения – логическая связка. С помощью связки обозначается утверждение или отрицание принадлежности предмету определенного признака.
Утвердительная связка выражается словом «есть», («является»), отрицательная – словом «не есть», («не является»).
Итак, S есть P – «студенты есть изучающие логику». Субъект – «студенты», предикат – «люди, изучающие логику».
Слайд 8Виды простых суждений
В традиционной логике установилось деление простых суждений по
характеру предиката. В соответствии с этим выделяются следующие виды простых
суждений:1) атрибутивные, т.е. суждения указывающие на свойство, присущее или неприсущее предмету (субъекту);
2) реляционные или с отношениями – суждения, указывающие на отношения между предметами;
3) существования (экзистенциальные суждения), отображающие факт существования или не существования того или иного предмета мысли.
Слайд 9Атрибутивные суждения
Логическая структура:
S есть (не есть) Р
«Есть» (суть) –
это логический термин, обозначающий логическую связь между S и Р,
т.е. принадлежность свойства предмету. В русском языке такая связка часто заменяется словом «является» или просто тире.Слайд 10Суждения с отношениями
Логическая структура: R (a,b)
где R
– отношение (например, «любить»),
a
- например, «Ромео»;b - например, «Джульетта».
В итоге получаем «Ромео любит Джульетту».
Отношение может быть многоместным:
R (a,b,c)
Слайд 11Суждения существования
Логическая форма суждения существования может быть записана так:
х
Р(х) – «существует такой х, который обладает свойством Р».
Слайд 12Доказательство бытия Бога
Бог, по определению, является максимально совершенным существом.
Предположим,
что ему не присущ признак существования.
Тогда мы можем представить
себе другое существо, в понятие которого входит этот признак. Значит, это существо будет более совершенным, чем Бог.
Но это противоречит нашей исходной посылке, что Бог - максимально совершенное существо.
Значит, наше предположение, что Бог не обладает признаком существования, неверно.
Следовательно, существование присуще Богу и суждение «Бог существует» является истинным. Следовательно, Бог существует.
Слайд 13Категорические суждения
Атрибутивные суждения, определенные по количеству и качеству, называются категорическими
Качество
суждения определяется его логической связкой: «есть» или «не есть».
Утвердительными
называются суждения, в которых говорится («утверждается») о принадлежности свойства предмету, т.е. «S есть Р» («Металлы – электропроводны»). Отрицательными называются суждения, в которых отрицается наличие свойство у предмета – «S не есть Р» («Золото не ржавеет»).
Количество суждения определяется объемом, в котором берется субъект, т.е. обо всех предметах идет речь или о некоторых. По количеству атрибутивные суждения делятся на общие («Все S есть Р») и частные («Некоторые S есть Р»).
Единичные суждения («Сократ – человек») приравниваются к общим, т.к. субъект в них берется в полном объеме.
Слайд 14Объединенная классификация
Общеутвердительные суждения. Стандартная форма: «Все S есть Р». Их
также принято сокращенно обозначать латинской буквой «А». Пример: «Все люди
есть существа, добрые по природе».Общеотрицательные суждения. Стандартная форма: «Ни один S не есть Р». Сокращенно обозначаются буквой «Е». Пример: «Ни один человек не есть совершенное существо».
Частноутвердительные суждения. Стандартная форма: «Некоторые S есть Р». Обозначаются буквой «I». Пример: «Некоторые люди есть существа, имеющие преступные наклонности».
Частноотрицательные суждения. Стандартная форма: «Некоторые S не есть Р». Обозначаются буквой «О». Пример: «Некоторые люди не есть существа, имеющие преступные наклонности».
Слайд 15Сокращенные наименования
Названия суждений громоздкие, произносятся не без труда. Для большего
удобства в логике применяются символические обозначения суждений большими буквами латинского
алфавита.А – общеутвердительное суждение;
I – частноутвердительное суждение;
Е – общеотрицательное суждение;
О – частноотрицательное суждение.
Из латинского слова affirmo – «утверждаю» первая гласная (A) обозначает общеутвердительное суждение, вторая гласная (I) частноутвердительное. Из латинского слова nego – «отрицаю» первая гласная (E) обозначает общеотрицательное суждение, вторая гласная (O) частноотрицательное.
Слайд 16Выделяющие суждения
Общие, частные и единичные суждения могут быть выделяющими.
Если
мы внимательно посмотрим на состав этих суждений, то заметим, что
в них четко установлен объем субъекта, а объем предиката неопределенный.В суждении «Все студенты нашей группы успешно сдали экзамен по логике» субъект – «студенты нашей группы» не содержит неопределенности, а вот в отношении предиката «успешно сдали экзамен по логике» этого сказать нельзя. Неясно, только ли студентами нашей группы успешно сдан экзамен, или студентами других групп тоже.
Эту неопределенность можно устранить, уточнив, что студенты нашей группы, и только они, успешно сдали экзамен по логике. Это и будет общее выделяющее суждение, в котором объем субъекта и предиката совпадают. Схема: Все S, и только S, есть P.
Такие суждения встречаются часто, они имеют большое значение и в теории, и в практике. «Суд, и только суд, решает вопрос о виновности обвиняемого». Этого не могут сделать ни следователь, ни прокурор, не говоря уж о журналистах. «Аренда, и только аренда, есть лучший способ использования земли», по крайней мере, так считают многие, учитывая исторический опыт России.
Слайд 17Исключающие суждения
По количеству, суждения могут быть исключающими.
В таких суждениях
выражается принадлежность некоторого признака всем предметам данного класса, за исключением
одного или нескольких из них. «Все студенты нашей группы (S), кроме Иванова (S1), сдали экзамен по логике» (P).Схема: «Все S, кроме S1, есть P». Или: «Все не S1 есть P».
Положения таких суждений усиливают точность и определенность в познании и практике. Приведем еще примеры двух исключающих суждений из правовой сферы. «Заочное разбирательство уголовных дел в судах не допускается, кроме случаев, предусмотренных федеральными законами» (Конституция Российской Федерации) и «Никто не имеет права войти в вашу квартиру без вашего согласия, кроме случаев, предусмотренных законом».
Слайд 18Распределенность терминов
в категорических суждениях
Термины суждения – субъект и предикат.
Термин,
объем которого полностью включен в объем другого термина или полностью
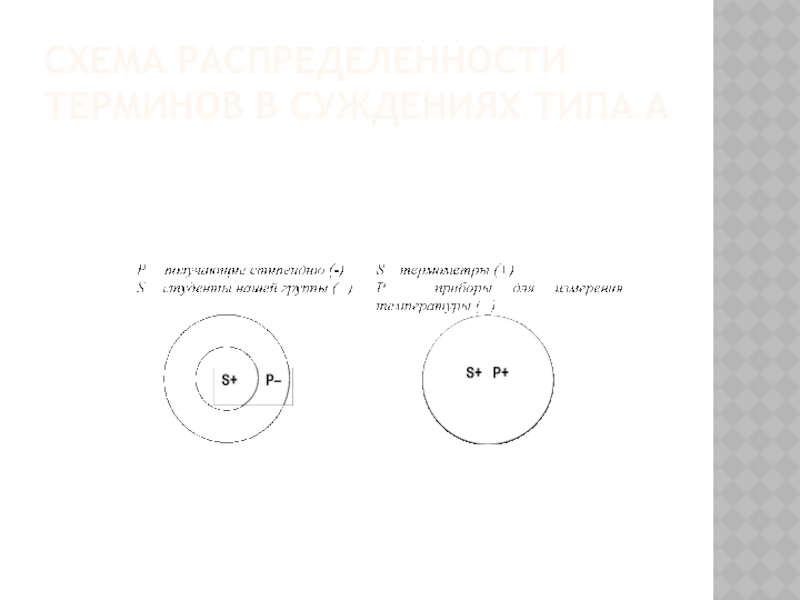
исключен из него, считается распределенным. Если же объем термина только частично включен в объем другого термина или частично исключен из него, то такой термин считается не распределенным.Слайд 19Суждения типа А
В общеутвердительном суждении S распределен (+), Р не
распределен (- ). Но если суждение выделяющее, или это части
определения, когда объемы понятий совпадают, то в таких суждениях оба термина распределены. «Все термометры (S+) есть приборы для измерения температуры (P+)».Слайд 21Суждение I (Некоторые S есть Р).
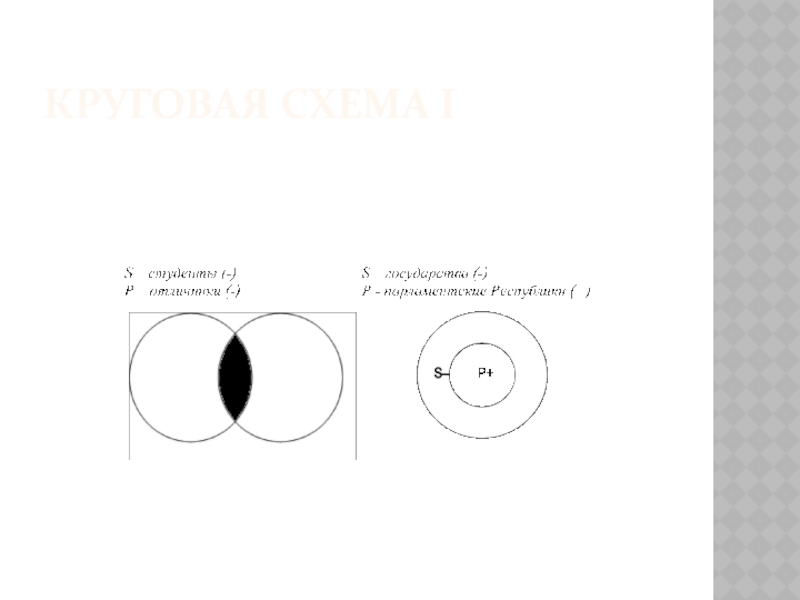
«Некоторые студенты (S) – отличники
(P)». И субъект «студенты», и предикат «отличники» частично входят в
объем друг друга. Часть студентов отличниками не являются, и часть отличников – не студенты (школьники, аспиранты). Значит, в частноутвердительном суждении субъект не распределен (-) и предикат не распределен (-).Но частноутвердительное суждение тоже может быть выделяющим. «Некоторые государства (S) есть парламентские республики (P)». Субъект «государства» не распределен, только часть из них относится к парламентским республикам, а предикат «парламентские республики» распределен, его объем полностью включается в объем понятия «государства». В выделяющем частноутвердительном суждении субъект не распределен (-), а предикат распределен (+).
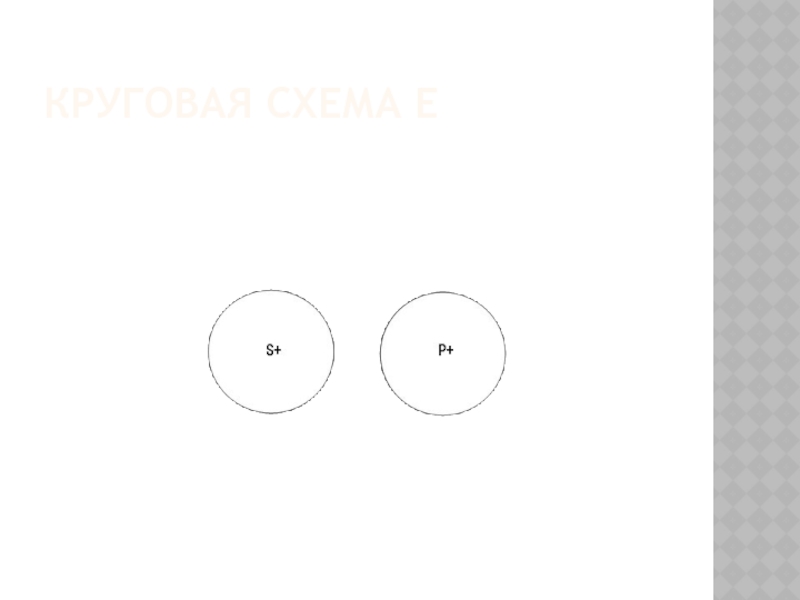
Слайд 23Суждение Е (Ни одно S не есть Р).
«Ни один студент
(S) не освобождается от экзамена по логике (P)».
И субъект
«студент», и предикат «освобожден от экзамена по логике» полностью исключаются из объема друг друга, значит, в общеотрицательном суждении субъект распределен (+) и предикат распределен (+).Слайд 25Суждение О (Некоторые S не есть Р)
«Некоторые студенты (S) не
являются отличниками (P)».
Субъект «студенты» не распределен, только часть студентов
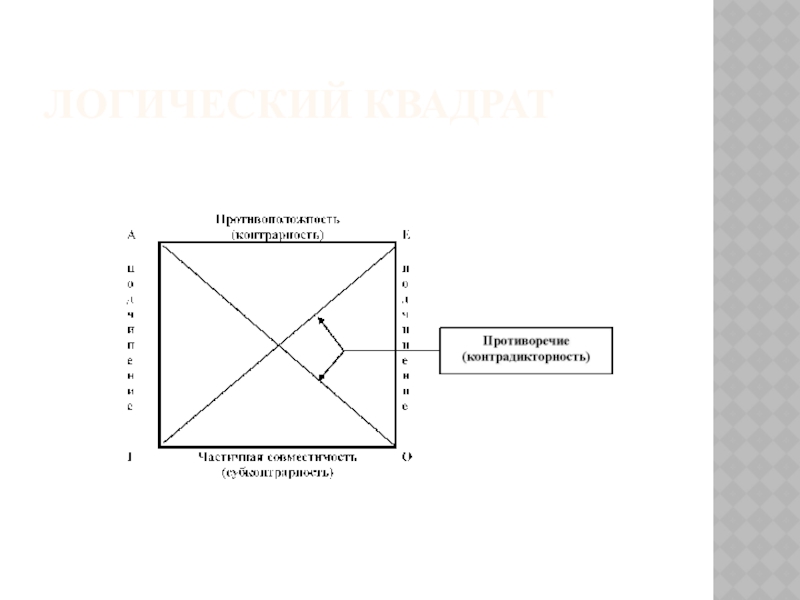
исключается из объема понятия «отличники». Предикат «отличники» распределен, его объем полностью исключается из той части студентов, которые отличниками не являются. Следовательно, в частноотрицательном суждении субъект не распределен (-), а предикат распределен (+).Слайд 29Отношения по логическому квадрату
Отношение между А и I, а также
между Е и О называется подчинением. Его основные свойства таковы:
если подчиняющее суждение (А или Е) истинно, то и подчиненное суждение (I или О) истинно, но не наоборот. Если подчиненное суждение ложно, то и подчиняющее суждение ложно, но не наоборот.На основании данного отношения можно строить элементарные умозаключения следующих видов:
Все S есть Р
Некоторые S есть Р
Ни один S не есть Р
Некоторые S не есть Р
¬(Некоторые S есть Р)
¬ (Все S есть Р)
¬ (Некоторые S не есть Р)
¬ (Ни один S не есть Р)
Слайд 30Противоположность
2. Суждения А и Е находятся в отношении противоположности (контрарности).
Это означает, что они не могут быть вместе истинными, но
могут быть вместе ложными, что позволяет обосновать и принять умозаключение вида:Все S есть Р
¬ (Ни один S не есть Р)
Слайд 31Противность
3. Суждения I и О находятся в отношении противности (субкотрарности),
т.е. они могут быть вместе истинными, но не могут быть
вместе ложными, что позволяет обосновать следующее непосредственное умозаключение по логическому квадрату:¬(Некоторые S есть Р)
Некоторые S не есть Р
Слайд 32Противоречие
4. Суждения А и О, а также Е и I
– расположенные на диагоналях квадрата - находятся в отношении противоречия
(контрадикторности). Это значит, что они не могут быть вместе ни истинными, ни ложными.Это обосновывает умозаключения следующих видов:
Все S есть Р
¬ (Некоторые S не есть Р)
Ни один S не есть Р
¬(Некоторые S есть Р)
¬(Все S есть Р)
Некоторые S не есть Р
¬(Ни один S не есть Р)
Некоторые S есть Р