TheSlide.ru

Свойства выборочных харрактеристик

Содержание

1. Свойства выборочных харрактеристик
2. Свойства среднего выборочногоПусть X – выборка объема
3. Свойства среднего выборочного2.
4. Свойства среднего выборочного3.4.
5. Свойства начальных моментов
6. Свойства выборочной дисперсии
7. Распределение χ2Распределением χ2 с k степенями свободы
8. Плотность распределения χ2 при k=7
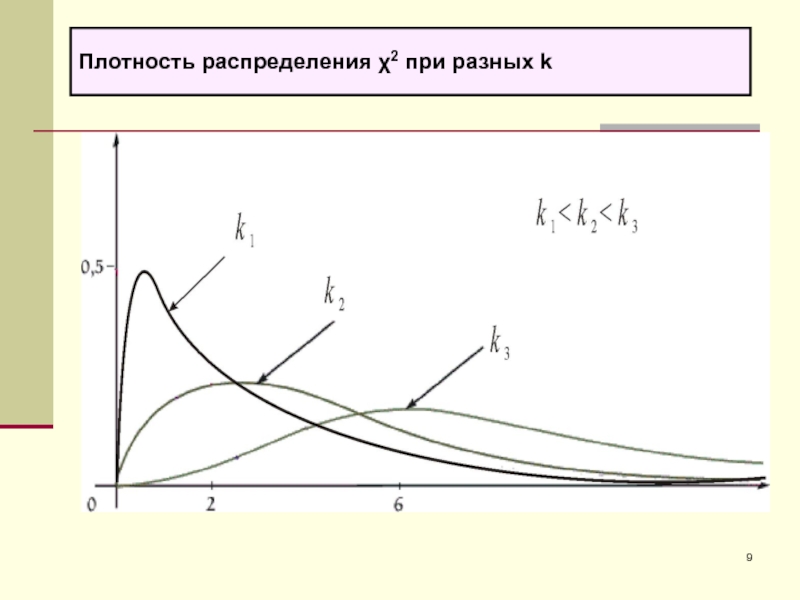
9. Плотность распределения χ2 при разных k
10. Плотность распределения χ2(k)
11. Замечание Если χ2(k1) и χ2(k2) независимые случайные величины,
12. Распределение Стьюдента Распределением Стьюдента с k степенями
13. Замечание Для приближенного выражения квантилей χ2p(k1) распределения χ2(k1)
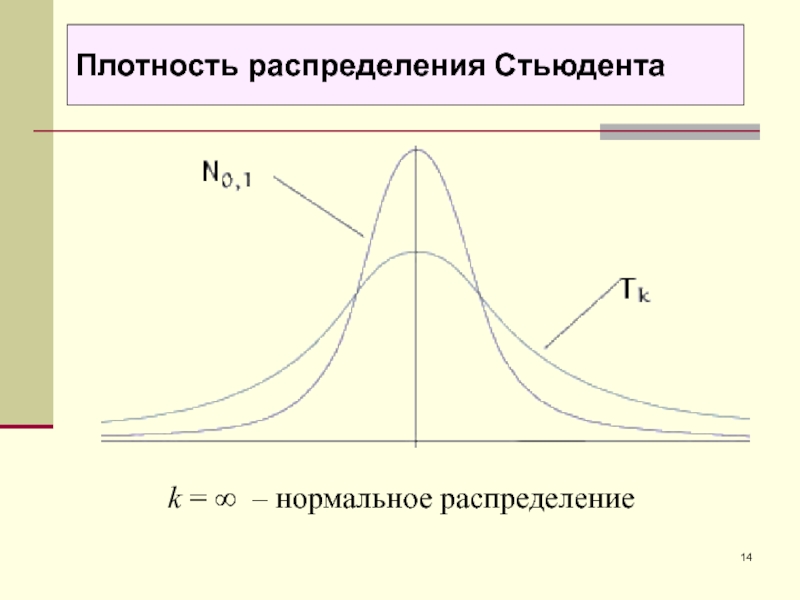
14. k = ∞ – нормальное распределениеПлотность распределения Стьюдента
15. Распределение Стьюдента с k степенями свободы имеет плотность Плотность распределения Стьюдента
16. Плотность распределения Стьюдента симметрична относительно оси ординат,
17. Распределение Фишера Распределением Фишера с k1 и k2
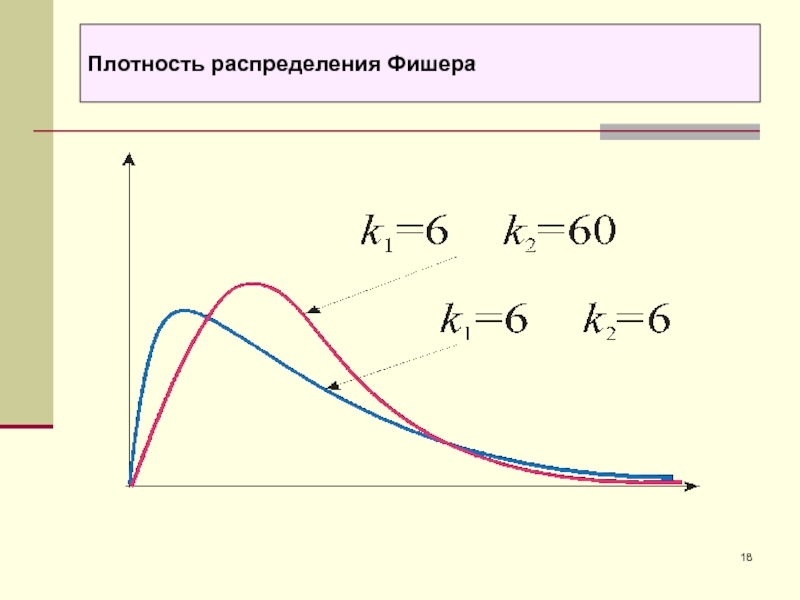
18. Плотность распределения Фишера
19. Распределение Фишера с k1 и k2 степенями свободы имеет плотность распределенияПлотность распределения Фишера
20. Матожидание распределения Фишера
21. Квантили распределения Фишера порядка p и 1 –p связаны соотношениемЗамечание
22. Между случайными величинами, имеющими нормальное распределение, распределение
23. Теорема Фишера Пусть (X1, X2,..., Xn) – выборка из N(a, σ). Тогда:
24. Теорема 1 Пусть (X1, X2,..., Xn) – выборка из N(a, σ). Тогда:
25. Скачать презентанцию

Свойства среднего выборочногоПусть X – выборка объема n значений случайной величины, имеющей матожидание a, дисперсию σ2. Тогда 1.

Главная
Разное
Свойства выборочных харрактеристик

Слайды и текст этой презентации

Слайд 1Теория вероятностей и математическая статистика
Свойства выборочных характеристик
ЛЕКЦИЯ 11

Теория вероятностей и математическая статистикаСвойства выборочных характеристикЛЕКЦИЯ 11

Слайд 2Свойства среднего выборочного
Пусть X – выборка объема n значений случайной

величины, имеющей матожидание a, дисперсию σ2. Тогда

1.

Свойства среднего выборочногоПусть X – выборка объема n значений случайной величины, имеющей матожидание a, дисперсию σ2. Тогда

Слайд 3Свойства среднего выборочного

2.

Свойства среднего выборочного2.

Слайд 4Свойства среднего выборочного

3.

4.

Свойства среднего выборочного3.4.

Слайд 5Свойства начальных моментов

Свойства начальных моментов

Слайд 6Свойства выборочной дисперсии

Свойства выборочной дисперсии

Слайд 7Распределение χ2
Распределением χ2 с k степенями свободы называется распределение случайной

величины χ2(k), равной сумме квадратов k независимых нормально распределенных по

закону N(0,1) случайных величин Ui i=1,2,…,k, т.е. распределение случайной величины

Распределение χ2Распределением χ2 с k степенями свободы называется распределение случайной величины χ2(k), равной сумме квадратов k независимых

Слайд 8Плотность распределения χ2 при k=7

Плотность распределения χ2 при k=7

Слайд 9Плотность распределения χ2 при разных k

Плотность распределения χ2 при разных k

Слайд 10Плотность распределения χ2(k)

Плотность распределения χ2(k)

Слайд 11Замечание
Если χ2(k1) и χ2(k2) независимые случайные величины, имеющие распределение χ2

с k1 и k2 степенями свободы соответственно, то сумма этих

случайных величин имеет распределение χ2 с k1+ k2 степенями свободы:
χ2(k1) + χ2(k2) = χ2(k1+k2)
Распределение χ2(k) при больших значениях k (k>30) с достаточной для практических расчетов точностью приближается нормальным распределением.

Замечание Если χ2(k1) и χ2(k2) независимые случайные величины, имеющие распределение χ2 с k1 и k2 степенями свободы соответственно,

Слайд 12Распределение Стьюдента
Распределением Стьюдента с k степенями свободы называется распределение

случайной величины Т(k), равной

где U имеет нормальное распределение N(0, 1).

Величина, имеющая распределение Стьюдента с k степенями свободы будет также обозначаться t(k).

Распределение Стьюдента Распределением Стьюдента с k степенями свободы называется распределение случайной величины Т(k), равной где U имеет нормальное

Слайд 13Замечание
Для приближенного выражения квантилей χ2p(k1) распределения χ2(k1) через квантили uр

нормального распределения N(0,1) используют следующие две формулы:

– формула

применяемая при k ≥ 30 и р ≥ 0.5

– формула применяется для вычисления квантилей малого порядка.

Замечание Для приближенного выражения квантилей χ2p(k1) распределения χ2(k1) через квантили uр нормального распределения N(0,1) используют следующие две формулы:

Слайд 14k = ∞ – нормальное распределение
Плотность распределения Стьюдента

k = ∞ – нормальное распределениеПлотность распределения Стьюдента

Слайд 15 Распределение Стьюдента с k степенями свободы имеет плотность

Плотность распределения

Стьюдента

Распределение Стьюдента с k степенями свободы имеет плотность Плотность распределения Стьюдента

Слайд 16 Плотность распределения Стьюдента симметрична относительно оси ординат, следовательно, для квантилей

tp(k) имеет место соотношение
tp(k)= – t1 –p(k).

При больших

k (k>30) для квантилей tp(k) распределения Стьюдента выполнено приближенное равенство
tp(k) ≈ up.

Замечание

Плотность распределения Стьюдента симметрична относительно оси ординат, следовательно, для квантилей tp(k) имеет место соотношение tp(k)= – t1

Слайд 17Распределение Фишера
Распределением Фишера с k1 и k2 степенями свободы называется

распределение случайной величины F(k1, k2), равной

Распределение Фишера Распределением Фишера с k1 и k2 степенями свободы называется распределение случайной величины F(k1, k2), равной

Слайд 18Плотность распределения Фишера

Плотность распределения Фишера

Слайд 19 Распределение Фишера с k1 и k2 степенями свободы имеет плотность

распределения
Плотность распределения Фишера

Распределение Фишера с k1 и k2 степенями свободы имеет плотность распределенияПлотность распределения Фишера

Слайд 20

Матожидание распределения Фишера

Матожидание распределения Фишера

Слайд 21 Квантили распределения Фишера порядка p и 1 –p связаны соотношением

Замечание

Квантили распределения Фишера порядка p и 1 –p связаны соотношениемЗамечание

Слайд 22 Между случайными величинами, имеющими нормальное распределение, распределение χ2, распределение Стьюдента

и распределением Фишера имеют место следующие соотношения
Замечание

Между случайными величинами, имеющими нормальное распределение, распределение χ2, распределение Стьюдента и распределением Фишера имеют место следующие соотношенияЗамечание

Слайд 23Теорема Фишера
Пусть (X1, X2,..., Xn) – выборка из N(a, σ).

Тогда:

Теорема Фишера Пусть (X1, X2,..., Xn) – выборка из N(a, σ). Тогда:

Слайд 24Теорема 1
Пусть (X1, X2,..., Xn) – выборка из N(a, σ).

Тогда:

Теорема 1 Пусть (X1, X2,..., Xn) – выборка из N(a, σ). Тогда:

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей