свойства гетерогенных систем. Эффективная диэлектрическая проницаемость

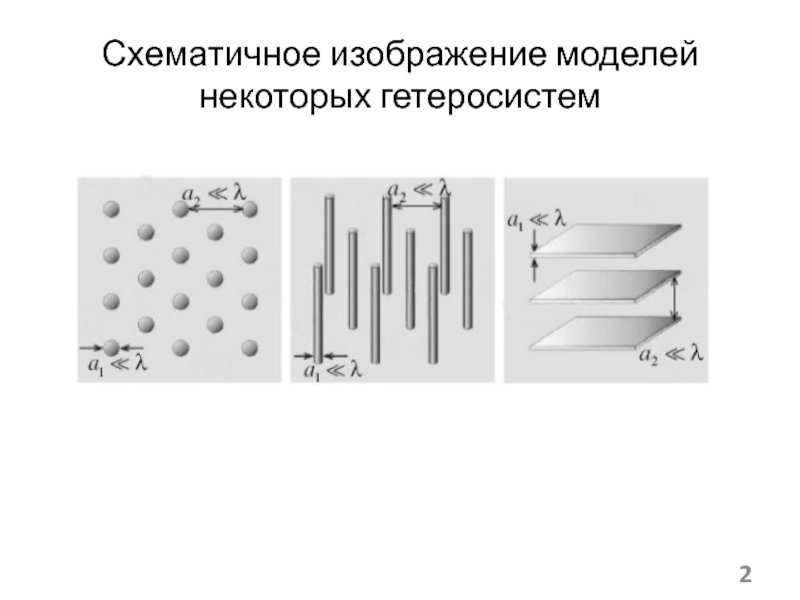
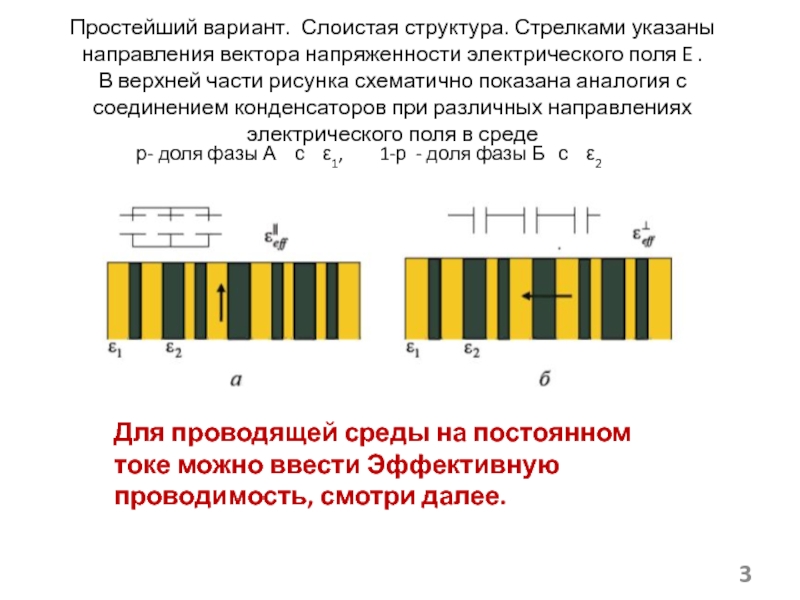
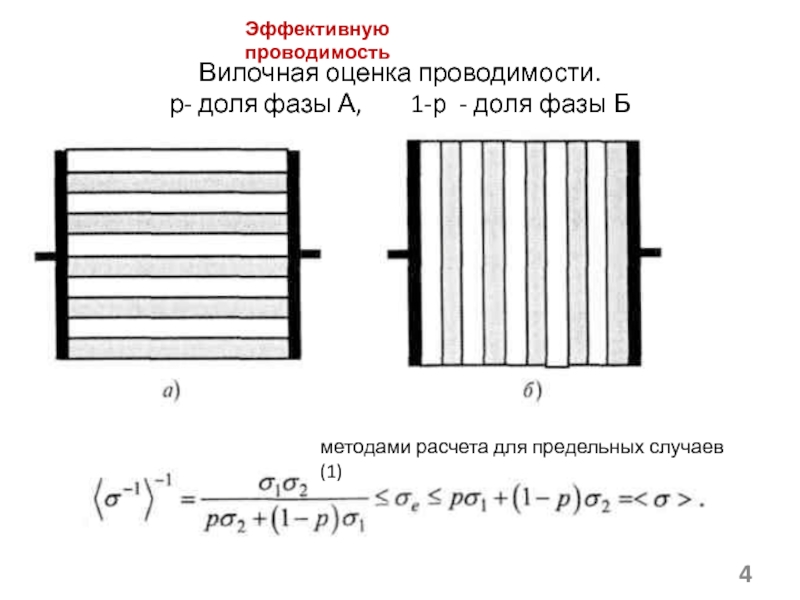
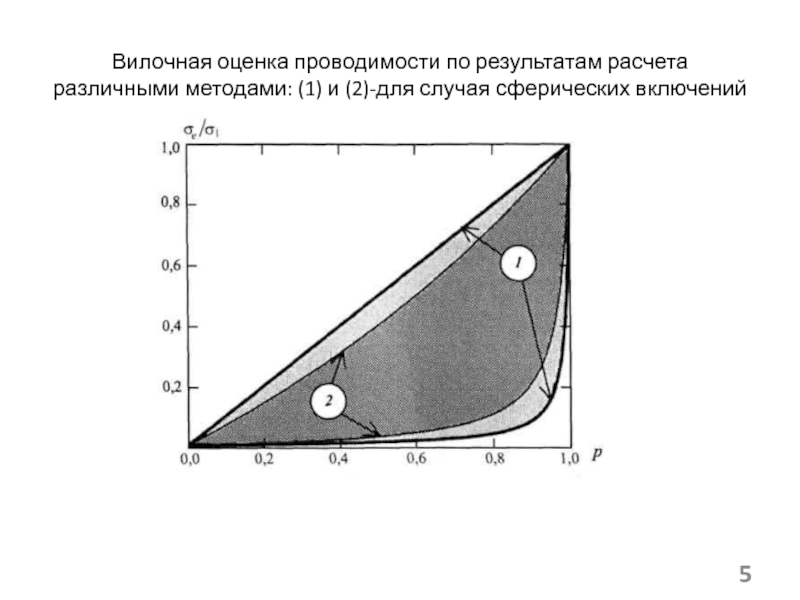
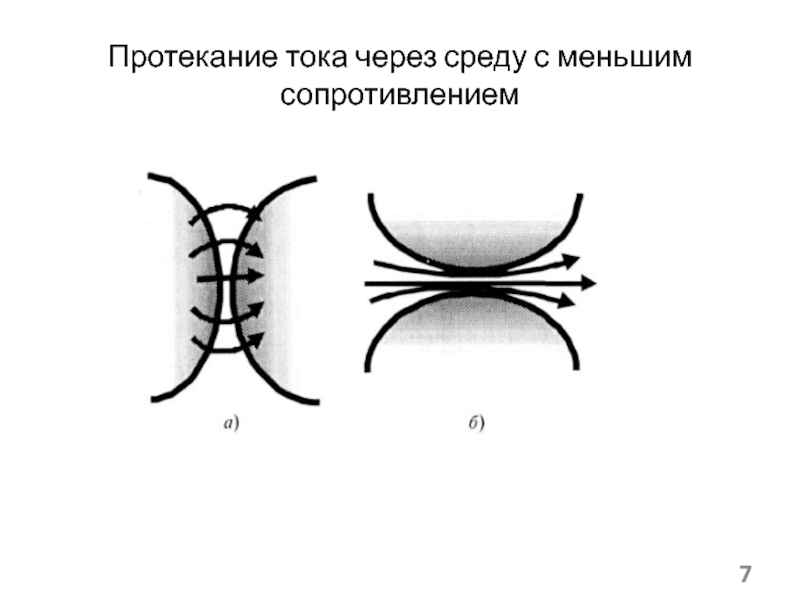
(а) и статистическая гетеросистема (б)
а

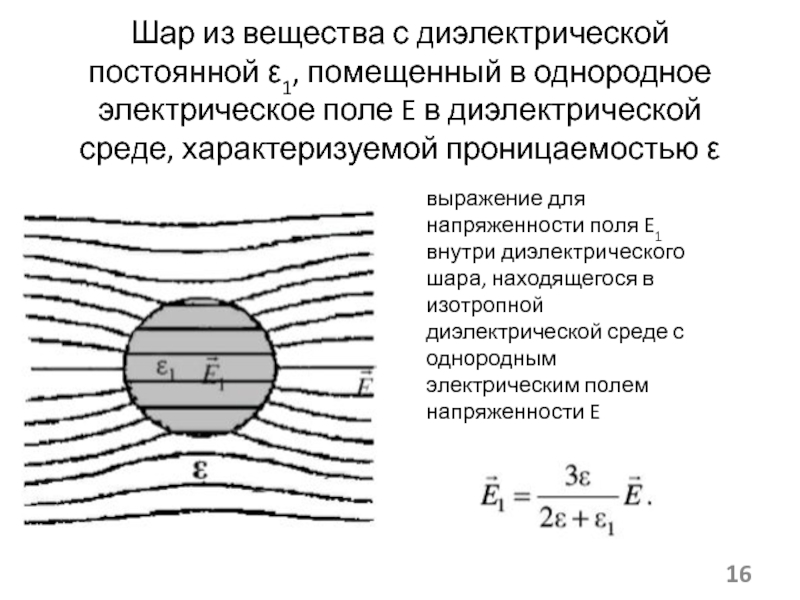
В этом случае эффективная диэлектрическая проницаемость εeff
композитной среды определяется уравнением

D= ε0εeff E

где D — средняя макроскопическая (усредненная по объему) вели-
чина вектора электрической индукции,
E — средний по объему вектор напряженности электрического поля в среде. Эффективная диэлектрическая проницаемость εeff может быть комплексной и, в случае анизотропных сред, тензорной величиной.

поля E . В верхней части рисунка схематично показана аналогия

с соединением конденсаторов при различных направлениях электрического поля в среде

Для проводящей среды на постоянном токе можно ввести Эффективную проводимость, смотри далее.

р- доля фазы А с ε1, 1-р - доля фазы Б с ε2

1-р - доля фазы Б
Эффективную проводимость
методами расчета для предельных случаев

(1)

(2)-для случая сферических включений

с диэлектрическими проницаемостями ε2 находится в некоторой эффективной среде. В

первом приближении форма включений считается сферической, а учет взаимодействия каждого шара со всеми окружающими его элементами гетеросистемы заменяется учетом взаимодействия со средой, характеризующейся эффективной диэлектрической проницаемостью εeff . При этом делается предположение, что на каждый шар действует поле, которое является усредненным по всему объему. В этом случае поля в каждом сферическом компоненте с диэлектрической проницаемостью εi , задаются выражением ниже, то есть однородны и имеют одинаковое направление: (здесь номер i=2)

E на большом расстоянии от него. Иначе говоря, это поле,

существующее «на бесконечности», то есть далеко от включения, в среде с диэлектрической проницаемостью ε1. Получим выражение для напряженности электрического поля внутри шара. Найдем вначале распределение потенциала в рассматриваемой системе. Выберем начало сферической системы координат в центре шара. Будем искать потенциал вне шара ϕ в виде суммы потенциала однородного приложенного поля и дополнительного вклада в потенциал, вызываемого шаром. Второе слагаемое должно обращаться в нуль на бесконечности, зависеть только от напряженности электрического поля E и являться решением уравнения Лапласа ∆φ = 0 . Можно показать, что данным условиям удовлетворяет единственная сумма, где А – некая константа: φ = −(E,r )+ A/r3 (1.58) Потенциал поля внутри шара ϕ1 будем искать в виде φ1 = -B(E,r ), (1.59)

электрическое поле E в диэлектрической среде, характеризуемой проницаемостью ε
выражение для

напряженности поля E1 внутри диэлектрического шара, находящегося в изотропной диэлектрической среде с однородным электрическим полем напряженности E

поле