Слайд 1U
A
B
Таблиці істинності, логіка, доведення.
Лекція 1
A
Слайд 2Література
Андерсон Дж. Дискретная математика и комбинаторика. – М. :
Изд. дом «Вильямс», 2003.
Новиков Ф.А. Дискретная математика для
программистов. – СПб: Питер, 2000.
Куликов Л. Я. Алгебра и теория чисел. - М.: Высшая школа, 1979.
Бардачов Ю.М. Дискретна математика: Підручник / за ред.
В.Є. Ходакова. – К.: Вища шк., 2002.
Яблонский С.В. Введение в дискретную математику. М.: Наука, 1981.
Слайд 3Висловлення і логічні зв’язки. Таблиці істинності
Умовні висловлення
Еквівалентні висловлення
Аксіоматичні
системи: умовиводу і доведення
Повнота в логіці висловлень
Карти Карно
Комутаційні
схеми
План
Слайд 4ВИСЛОВЛЕННЯ І ЛОГІЧНІ ЗВ'ЯЗКИ
Висловлення – це твердження або розповідне
речення, про зміст
якого можна сказати, істинне воно або хибне.
Значення
істинності висловлень - «Iстинно» і «Хибно»
позначають відповідно символами 1 і 0, T i F або I і Х.
Справедливі наступні закони.
Закон виключеного третього. Кожне висловлення є або
істинним, або хибним.
Закон виключення суперечності. Жодне висловлення не є
одночасно істинним і хибним.
Змінні висловлення позначають латинськими літерами (р, q, r,
r1, …). Після підстановки певного елементарного висловлення змінне висловлення набуває відповідного значення: 0 або 1.
Приклади. 1. p: «Херсон – це обласний центр».
2. q: «Земля обертається».
Слайд 5Приклади висловлень:
1. Число 5 є простим.
2. Усі натуральні числа парні.
3.
Херсон – це обласний центр.
4. Множина всіх непарних чисел є
скінченною.
Перше і третє висловлення - істинні, друге і четверте - хибні.
Приклади речень, що не є висловленнями:
1. Хто ви? (питання)
2. Прочитайте цей розділ до наступного заняття.
3. Хай живе математика!
4. Будьте обережні. (наказ або вигук)
5. Це твердження хибне. (внутрішньо суперечливе твердження)
Слайд 6
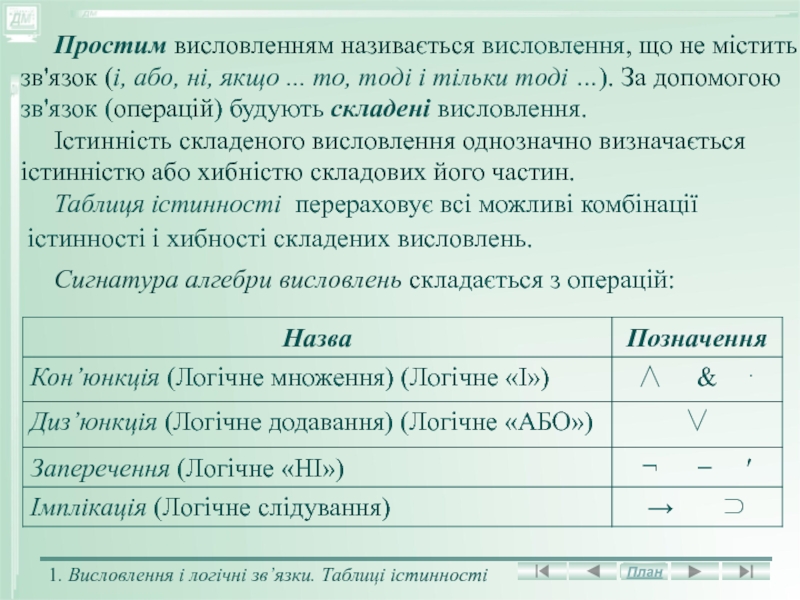
Простим висловленням називається висловлення,
що не містить зв'язок (і, або, ні, якщо ... то,
тоді і тільки тоді …). За допомогою зв'язок (операцій) будують складені висловлення.
Істинність складеного висловлення однозначно визначається істинністю або хибністю складових його частин.
Таблиця істинності перераховує всі можливі комбінації
істинності і хибності складених висловлень.
Сигнатура алгебри висловлень складається з операцій:
Слайд 7 Кон’юнкцією висловлень p і q називається складене
висловлення, яке істинне, коли істинні його обидві складові, та символічно
може бути записане у вигляді p q.
Таблиця істинності кон’юнкції
Приклад. Нехай р і q позначають висловлення р: Діна водить авто, q: У Бориса темне волосся. Складене висловлення Діна водить авто і у Бориса темне волосся складається з двох частин, об'єднаних зв'язкою і.
Слайд 8 Диз'юнкцією висловлень р і q називається
складене висловлення р q, яке істинне, коли істинна одна
із двох його складових.
Таблиця істинності диз'юнкції
Приклад. Висловлення Діна водить авто або у Бориса темне волосся є складеним і символічно може бути записане у вигляді
р q. Для того щоб це висловлення було істинним, достатньо, щоб була істинною одна з його складових.
Слайд 9 Заперечення висловлення р позначається через ~p. Значення
~р завжди протилежне значенню істинності р.
Таблиця істинності для заперечення
р
Приклад. Якщо р є висловлення Діна водить автомобіль, то ~р
є твердження Діна не водить автомобіль.
У таблицях істинності заперечення простого висловлення оцінюється першим. Тому ~p q означає (~р) q, заперечення всього висловлення p q записується як ~(p q).
Символи і називають бінарними зв’язками, оскільки вони
зв'язують два висловлення як, наприклад, у виразах р q і р q.
Символ ~ є унарною зв’язкою, тому що застосовується тільки
до одного висловлення.
Слайд 10 Виключаючим або висловлень р і q називається складене
висловлення
р q, яке істинне, коли істинне р або q,
але не обоє
одночасно.
Виключаюче або має таблицю істинності
Таблиця істинності дає можливість однозначно вказати ті ситуації, коли висловлення є істинним; при цьому враховуються всі випадки.
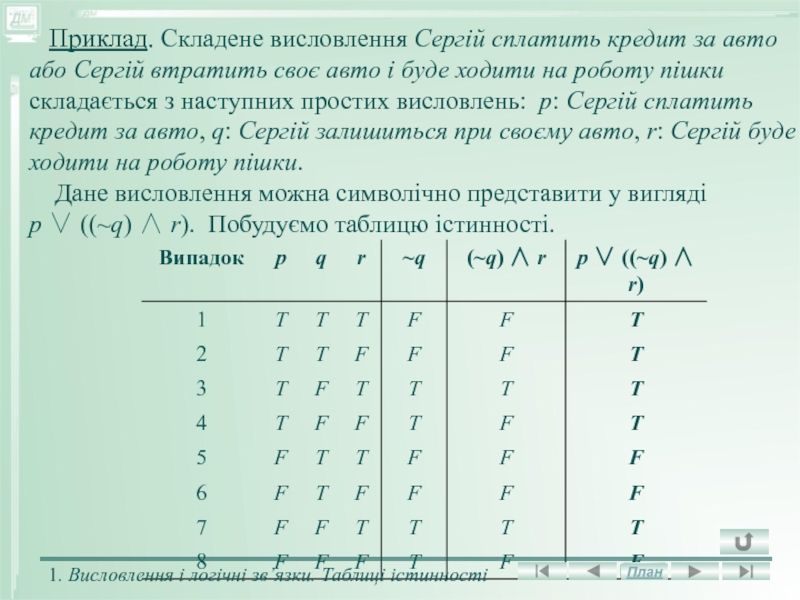
Слайд 11 Приклад. Складене висловлення Сергій сплатить кредит за авто
або Сергій втратить своє авто і буде ходити на роботу
пішки складається з наступних простих висловлень: р: Сергій сплатить кредит за авто, q: Сергій залишиться при своєму авто, r: Сергій буде ходити на роботу пішки.
Дане висловлення можна символічно представити у вигляді
p ((~q) r). Побудуємо таблицю істинності.
Слайд 12 УМОВНІ ВИСЛОВЛЕННЯ
Імплікацією, або умовною зв'язкою називається складене
висловлення p
→ q, яке хибне лише у випадку, коли p -
істинне, а
q – хибне. При цьому р називають припущенням, q – висновком.
Таблиця істинності для висловлення р → q
Приклад. Висловлення Якщо в цьому семестрі ти складеш всі
іспити на «відмінно», то отримаєш підвищену стипендію має
вигляд: якщо р, то q, де р - висловлення В цьому семестрі ти
складеш всі іспити на «відмінно», a q - висловлення Отримаєш
підвищену стипендію.
Слайд 13 Еквіваленцією називається висловлення р ↔ q, що
істинне тільки у випадку, коли р і q мають однакові
значення істинності. Висловлення р ↔ q позначає висловлення виду (р → q) (q → р).
Таблиця істинності для р ↔ q
визначається таблицею істинності для (р → q) (q → р).
Пріоритет виконання операцій.
Операції виконуються у наступній послідовності:
~, , , → і ↔.
Слайд 14 Логічно еквівалентними називаються складені висловлення,
що мають різну
будову, але є істинними в тих самих випадках.
Приклад. Нехай р і q є висловленнями р: Сьогодні йшов дощ,
q: Сьогодні йшов сніг. Розглянемо складені висловлення.
Невірно, що сьогодні йшов дощ або сніг: ~(p q)
Сьогодні не йшов дощ і сьогодні не йшов сніг: ~p ~q
Таблиці істинності для обох висловлень.
ЕКВІВАЛЕНТНІ ВИСЛОВЛЕННЯ
У таблиці істинності значення для ~(р q) і для ~р ~q збігаються, тобто розглянуті висловлення логічно еквівалентні:
~(р q) ≡ ~р ~q.
Слайд 15Конверсія, інверсія й контрапозиція
З умовним висловленням - імплікацією р
→ q - пов'язані три
типи висловлень: конверсія, інверсія й контрапозиція
висловлення
р → q. Вони означуються в такий спосіб:
р → q – імплікація
q → р – конверсія висловлення р → q
~р → ~q – інверсія висловлення р → q
~q → ~р – контрапозиція висловлення р → q
Приклад. Нехай дано висловлення-імплікація
Якщо він грає у футбол, то він популярний.
Для цієї імплікації маємо:
конверсія: Якщо він популярний, то він грає у футбол.
інверсія: Якщо він не грає у футбол, то він не популярний.
контрапозиція: Якщо він не популярний, то він не грає у футбол.
Слайд 16 Умовні висловлення можуть виражатися у вигляді різних мовних
конструкцій,
які символічно записуються як р → q.
якщо р, то
q. р, тільки якщо q (тільки якщо q, то р)
р достатньо для q. q необхідно для р.
р є достатньою умовою для q. q є необхідною умовою для р.
Еквіваленція р ↔ q означає р тоді й тільки тоді, коли q, або
р якщо й тільки якщо q.
Приклад. Для висловлень р: Денис буде грати у футбол, q: Діна організує підтримку глядачів висловлення р ↔ q може означати: Денис буде грати у футбол, якщо й тільки якщо Діна організує підтримку глядачів.
Наступні мовні конструкції, що виражають еквіваленцію висловлень р ↔ q, рівносильні:
р якщо й тільки якщо q. р необхідно й достатньо для q.
р є необхідна й достатня умова для q.
Слайд 17Закони ідемпотентності:
p p ≡ p;
p p ≡ p.
Закон
подвійного заперечення:
~ (~p)≡ p.
Закони де Моргана:
~ (p q) ≡
~p ~q;
~ (p q) ≡ ~p ~q.
Властивості комутативності:
p q ≡ q p;
p q ≡ q p.
Властивості асоціативності:
p (q r) ≡ (p q) r;
p (q r) ≡ (p q) r.
Властивості дистрибутивності:
p (q r) ≡ (p q) (p r);
p (q r) ≡ (p q) (p r).
Закон контрапозиції:
p → q ≡ ~q → ~р.
Інші корисні властивості:
p → q ≡ ~p q;
p ↔ q ≡ (р → q) (q → р).
Властивості логічних звязок
ТЕОРЕМА. Використовуючи таблиці істинності, можна довести наступні логічні еквівалентності:
Слайд 18Тавтологія та протиріччя
Тавтологією, або логічно істинним висловленням називається
висловлення, істинне у
всіх випадках; висловлення, хибне у
кожному випадку, називається логічно хибним
або протиріччям.
Висловленню (p (p → q)) → q відповідає таблиця істинності
Символ Т позначає висловлення, що є тавтологією, тому має таблицю істинності, що складається з одних Т. Символ F позначає протиріччя, тобто висловлення, таблиця істинності якого містить F у всіх рядках.
Слайд 19Співвідношення зі сталими
Закони одиниці і нуля:
p T ≡
p, p T ≡ T,
p F
≡ F, p F ≡ p;
закони протиріччя та виключеного третього:
p ~ p ≡ F, p ~ p ≡ T;
p → p ≡ T.
Правило заміни. Після заміни будь-якої компоненти висловлення
на логічно еквівалентне висловлення буде отримано висловлення,
логічно еквівалентне вихідному. Наприклад, (q r) (p ~r) ≡
≡ q (r (p ~r)) ≡ властивість асоціативності
≡ q ((r p) (r ~r)) ≡ властивість дистрибутивності
≡ q ((r p) T) ≡ еквівалентність
≡ q (r p) ≡ еквівалентність
≡ q (p r) ≡ властивість комутативності
≡ (q p) r ≡ властивість асоціативності
≡ (p q) r властивість комутативності
Слайд 20АКСІОМАТИЧНІ СИСТЕМИ:
УМОВИВОДУ І ДОВЕДЕННЯ
Аксіомами (постулатами) називають неозначуванні поняття
і
твердження, що використовують для утворення математичної
системи і які точно
описують фундаментальні характеристики
або істинні твердження щодо цих понять.
Теоремами називаються твердження, виведені (доведені) на
основі тільки фундаментальних властивостей (постулатів і аксіом)
і раніше доведених тверджень за допомогою логічних правил.
Правилами виведення називаються логічні правила, за
допомогою яких доводять нові теореми з аксіом, постулатів і
раніше доведених у даній системі теорем, і які не породжують у
якості "теорем" хибні висловлення.
Умовивід складається із сукупності тверджень, названих
гіпотезами, і твердження, названого висновком. Гіпотези – це
перелік одного або більше висловлень (посилок).
Слайд 21 Умовиводи представляють у вигляді
H1
H2 гіпотези (припущення, посилки)
H3
C висновок (наслідок)
Правильним умовиводом називається умовивід, висновок
якого істинний щораз, коли істинні його гіпотези (щораз, коли
(H1 H2 H3 - істинно) → (істинне і С).
Правила виведення обирають так, щоб вони були правильними
умовиводами.
Правильність умовиводу можна перевірити двома способами.
1 спосіб: побудувати таблицю істинності й показати, що щораз, коли гіпотези істинні, істинний і висновок.
2 спосіб: використати таблиці істинності для обґрунтування правил виведення, а потім використати правила виведення для доведення справедливості висновку.
Слайд 22 Приклад 1. Розглянемо умовивід
p
p →
q
q → r
р
q r
Таблиці істинності для посилок і висновку:
Коли істинні всі посилки (випадок 1), істинним є і висновок, а сам умовивід є правильним.
Слайд 23 Приклад 2. Розглянемо умовивід
p q
p
→ r
q → r
r
Таблиці істинності для посилок
і висновку:
Коли всі посилки істинні (випадки 1, 3 і 5), висновок істинний, і умовивід правильний.
Слайд 24 Приклад 3. Розглянемо умовивід
p → q
q
→ r
r
p
Таблиці істинності для посилок і висновку:
У випадку 1 істинні і посилки, і висновок, а у рядках 5 і 7 посилки істинні, а висновок хибний. Отже, умовивід не є правильним.
Слайд 25 Метод направлений на доведення неправильності висновку. У
разі успіху такого доведення
це буде свідоцтвом неправильності
умовиводу.
Якщо, припускаючи неправильність умовиводу, приходимо до
суперечності,
то умовивід є правильним.
Наприклад, розглянемо умовивід
p q
p → r
q → r
r
Якщо умовивід неправильний, існують значення істинності р, q
і r, для яких посилки істинні, а висновок хибний.
Якщо висновок хибний, то r хибне.
Якщо q → r істинне, а r хибне, то q хибне.
Якщо р → r істинне, тоді р хибне.
Але тоді р q хибне, що суперечить твердженню, що висновок
хибний, а посилки істинні. Отже, умовивід правильний.
Метод від супротивного (протилежного).
Слайд 26 Будь-який умовивід з посилками Н1, H2, H3, ..., Hn і
висновком C
є правильним тоді і тільки тоді, коли висловлення
(H1 Н2 H3 … Нn) → C
є тавтологія.
Порядок проходження посилок не є істотним, оскільки
Н1 Н2 Н2 Н1.
Приймемо у якості правила виведення наступний умовивід, в
правильності якого легко переконатися.
p
p → q
q
Цей правильний умовивід називається правилом висновку
(відокремлення) (modus ponens).
Слайд 27 Приклад. Розглянемо приклад використання правила
відокремлення. Нехай b -
ціле число, а р і q задані таким чином: р: b
парне; q: b ділиться на 2,
отже
p → q: якщо b парне, то b ділиться на 2
Правило відокремлення дає
р → q якщо b парне, то b ділиться на 2
p b парне
q b ділиться на 2
Припустимо, що висловлення якщо b парне, то b ділиться на 2
одержано як властивість цілих чисел і b = 12. Тоді обидві посилки
істинні, так що немає сумніву у тому, що 12 ділиться на 2.
З другого боку, якщо b = 13, тоді р хибне, і хоча умовивід
правильний, не можна стверджувати що-небудь про подільність
b = 13 на 2. Якщо одна з посилок хибна, то істинність висновку
жодним чином не залежить від правильності умовиводу.
Слайд 28Правила виведення
а) Modus Ponens
б) Силогізм
в) Modus
Tollens
г) Розширення
д) Спеціалізація
е) Кон'юнкція
ж) Вибір
з)
Виключаючий
вибір
и) Зведення до
абсурду
Правильність всіх перерахованих умовиводів можна показати за допомогою таблиць істинності.
Слайд 29 Зведення до абсурду використовується у методі доведення від
супротивного (протилежного).
Припускаємо, що істинним є
заперечення висловлення, яке необхідно довести, і намагаємося
дійти суперечності. Якщо це вдається, твердження доведено.
Розглянемо умовиводи:
Таблиця істинності даних умовиводів.
Таблиця істинності показує хибність обох умовиводів. 1-й з
них називають помилкова конверсія, а 2-й – помилкова інверсія.
Слайд 30 Приклад. Нехай дані висловлення
р: яблуко червоне,
q: яблуко стигле.
помилкова конверсія
приймає вигляд
помилкова інверсія
приймає вигляд
Слайд 31Процес доведення теорем
Доведення – це послідовність тверджень, кожне з яких
істинне
через одну з наступних причин: а) за припущенням;
б) за
аксіомою або означенням;
в) за раніше доведеною теоремою або лемою;
г) виведено з попередніх тверджень;
д) логічно еквівалентно попередньому твердженню.
Приклад. Довести правильність даного умовиводу:
Доведення.
Слайд 32ПОВНОТА В ЛОГІЦІ ВИСЛОВЛЕНЬ
Одне з застосувань таблиць істинності - конструювання
комутаційних схем.
Оскільки
р ↔ q еквівалентно (р → q)
(q → р),
р q еквівалентно (р ~q) (~р q),
р → q еквівалентне ~р q,
p q еквівалентно ~(~р ~q),
p q еквівалентно ~(~р ~q).
то використовувати зв'язки ↔, , →, , зручно, але не необхідно.
Отже, висловлення може бути виражене через пару зв'язок
~ і або ~ і .
Слайд 33Але існують дві зв'язки, такі що висловлення може бути
виражене з використанням тільки однієї з них:
- штрих
Шеффера, - стрілка Пірса.
Їх таблиці істинності:
Еквівалентність р | р і ~р встановлюється за допомогою таблиці істинності:
Слайд 34Для того, щоб показати, що будь-яку зв'язку можна
замінити зв'язкою |,
достатньо показати це для пар зв'язок
~ і або ~
і , оскільки можливість виразити будь-яку
зв'язку однією з цих пар вже показана. Еквівалентність р | р
і ~р встановлюється за допомогою наступної таблиці
істинності:
Слайд 35Так само таблиця
показує, що (р | р) | (q|
q) еквівалентне р q. Можна також
показати, що (р |
q) | (p | q) еквівалентно р q.
Таким чином, якщо показати, що ~ і або ~ і можна
виразити, використовуючи тільки , тоді і будь-яку зв'язку
можна виразити, використовуючи лише .
Слайд 36Наприклад, припустимо, що є таблиця істинності
Відомо, що p q
істинне у випадку 1 і хибне у всій решті
випадків. Аналогічно,
р ~q істинне тільки у випадку 2,
~p q істинне тільки у випадку 3, а ~р ~q істинне тільки у
випадку 4. Нехай висловлення повинно бути істинним точно
у вказаних нами випадках. Якщо для кожного такого
випадку (рядка таблиці) вибрати висловлення, яке істинне
тільки в цьому випадку, і зв'язати ці висловлення зв'язкою ,
то отримаємо висловлення, істинне тільки в необхідних
випадках (рядках).
Слайд 37У приведеному вище прикладі дана таблиця істинності
відповідає висловленню (р
q) (р ~q) (~р ~q) .
У
разі таблиць істинності з трьома змінними маємо
аналогічну ситуацію. Для кожного рядка наступної таблиці
наведене висловлення, істинне тільки для цього рядка.
Слайд 38(р q ~r) (р ~q
r) (р q ~r)
Така форма виразу висловлення
називається диз'юнктивною
нормальною формою. Вирази р q ~r, р ~q r і
~р q ~r називаються елементарними кон'юнкціями.
ОЗНАЧЕННЯ 1.5. Нехай p1, p2, р3,…, рn - прості висловлення. Вираз х1 х2 x3 … хn, в якому хi = рi або
xi =~pi, назвемо елементарною кон'юнкцією. Вираз, що є диз'юнкцією елементарних кон'юнкцій, називається диз'юнктивною нормальною формою, тобто якщо m1, m2, m3, ..., mn - елементарні кон'юнкції, тоді m1 m2 m3 … mn - диз'юнктивна нормальна форма.
Хоча будь-яке висловлення може бути виражене в
диз'юнктивній нормальній формі, ця форма не є простою.
Слайд 39кожен вираз хибний в рядку, де він розташований, і істинний
в будь-якому іншому рядку. Якщо треба знайти висловлення, що відповідає
даній таблиці істинності, то використовують висловлення, кожне з яких хибне тільки у відповідному рядку, і всі ці висловлення об'єднуються зв'язкою .
Слайд 40Наприклад, таблиці істинності вигляду
відповідає висловлення
(~р q
~ r) (~р q r)
(р ~q r) (р q ~r) .
Слайд 41Така форма виразу висловлення називається кон'юнктивною нормальною формою. Вирази ~р
q ~r, ~p q r, p
~q r і p q ~r носять назву елементарних диз'юнкцій. Тепер дамо формальніше означення
Слайд 42КАРТИ КАРНО
Для простих висловлень p1, p2, p3,…, pn існує
2n різних
елементарних кон'юнкцій.
Наприклад, для висловлень р і q елементарними
кон'юнкціями
будуть р q, p ~q, ~р q і ~р ~q.
Карта Карно – це таблиця, кожен елемент якої є
елементарною кон'юнкцією.
Наприклад, для висловлень р і q карта Карно повинна мати
вигляд, зображений на рис. 1.1, а на рис. 1.2 усередині
прямокутників представлені відповідні елементарні
кон'юнкції.
Слайд 43Для представлення картою Карно висловлення, записаного в диз'юнктивній нормальній формі,
необхідно помістити в прямокутниках, відповідних елементарним кон'юнкціям. Наприклад, висловленню
(р q) (~р ~q) відповідає карта Карно, зображена на рис. 1.3.
Помітимо, що якщо висловленню відповідає карта Карно з двома сусідніми в рядку або в стовпці , тоді вираз можна спростити, звівши дві елементарні кон'юнкції до однієї, що містить на одну компоненту менше (тобто або р, або q не присутні у виразі).
Слайд 44Наприклад, висловлення (р q) (р ~q), якому
відповідає карта Карно, зображена на рис. 1.4, еквівалентна висловленню p,
оскільки (p q) (p ~q) p (q ~q) р Т р.
q -q
r -r r Рис. 1.5
Карта Карно для р, q і r може мати вигляд, зображений на
рис. 1.5, а на рис. 1.6 в прямокутниках всередині представлені елементарні кон'юнкції.
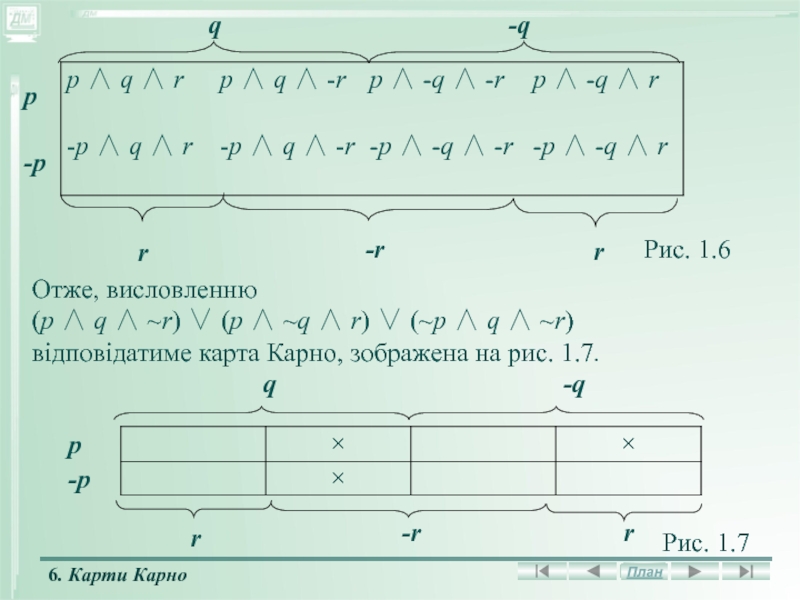
-q
r
-r
r
Рис. 1.6
Отже, висловленню
(р q ~r) (р ~q r) (~р q ~r)
відповідатиме карта Карно, зображена на рис. 1.7.
q -q
r
-r
r
Рис. 1.7
Слайд 46Перерахуємо чотири послідовні кроки при використанні карти Карно:
1. Для
кожної елементарної кон'юнкції позначте на карті відповідний прямокутник.
2. Покрийте
знаки, використовуючи, по можливості, декілька прямокутних блоків.
3. Використовуйте блоки, максимальні за величиною, не міняючи числа блоків.
4. Оцініть блоки з відповідними висловленнями, які описують їх, і об'єднайте ці висловлення символом .
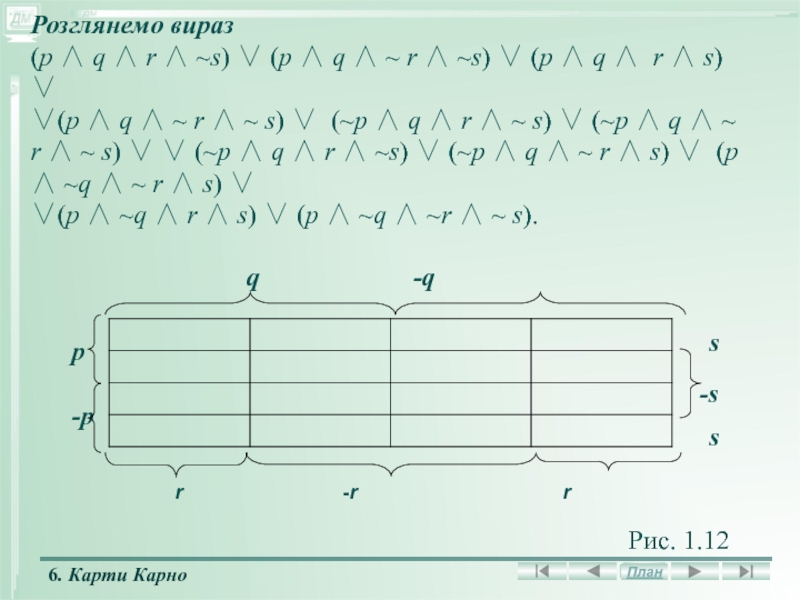
Слайд 47Розглянемо вираз
(р q r ~s)
(р q ~ r ~s) (р
q r s)
(р q ~ r ~ s) (~р q r ~ s) (~р q ~ r ~ s) (~р q r ~s) (~р q ~ r s) (р ~q ~ r s)
(р ~q r s) (р ~q ~r ~ s).
r -r r
q -q
s
s
-s
Рис. 1.12
Слайд 48Розміщуючи відповідні значки в карті Карно, отримуємо карту, зображену на
рис. 1.13, яку можна покрити восьмикратним, чотирикратним і двократним блоками.
Восьмикратний блок можна описати, використовуючи тільки одну з компонент р, q, r або s. В даному випадку восьмикратний блок описує q. Чотирикратний блок можна описати, використовуючи тільки два прості висловлення. В даному випадку цей блок можна описати, використовуючи р s. Двократний блок можна описати, використовуючи три прості висловлення. В даному випадку це р ~q r. Отже, початкове висловлення можна спростити і привести до вигляду q (p s) (р ~q r). Оскільки r знаходиться на обох кінцях рядка, а s знаходиться на обох кінцях стовпця, "скручування" карти Карно об'єднує ці
Слайд 49Рис. 1.13
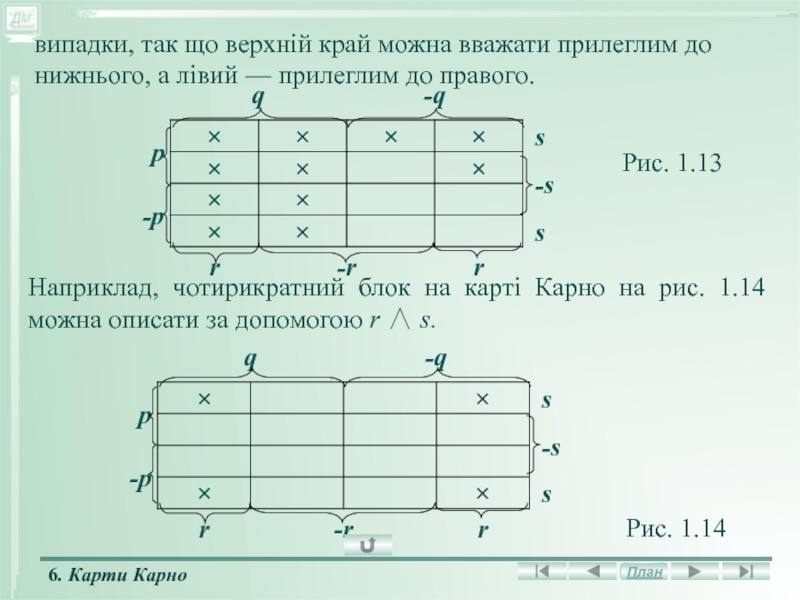
Наприклад, чотирикратний блок на карті Карно на рис. 1.14
можна описати за допомогою r s.
Рис. 1.14
випадки, так що
верхній край можна вважати прилеглим до нижнього, а лівий — прилеглим до правого.
Слайд 50КОМУТАЦІЙНІ СХЕМИ
Висловлення, відповідні комутаційним (релейно-контактним)
схемам, прийнято виражати у системі
позначень булевої алгебри. Тому, перш ніж перейти до вивчення комутаційних
схем, ми перейдемо від позначень, прийнятих в логіці, до булевого запису. Символи , і ~ замінюються, відповідно, на , + і '. Таким чином, (р q) ~r перетворюється в (р q) + r', а
(р q ~r) (р ~q r) (~р q ~r)
приймає вигляд
(р q r') + (р q' r) + (р' q r').
Як і в звичайній алгебрі, знак множення, як правило, опускається, і передбачається, що множення виконується перед додаванням, тому наведений вище вираз можна переписати у вигляді
pqr + pq'r + p'qr'.
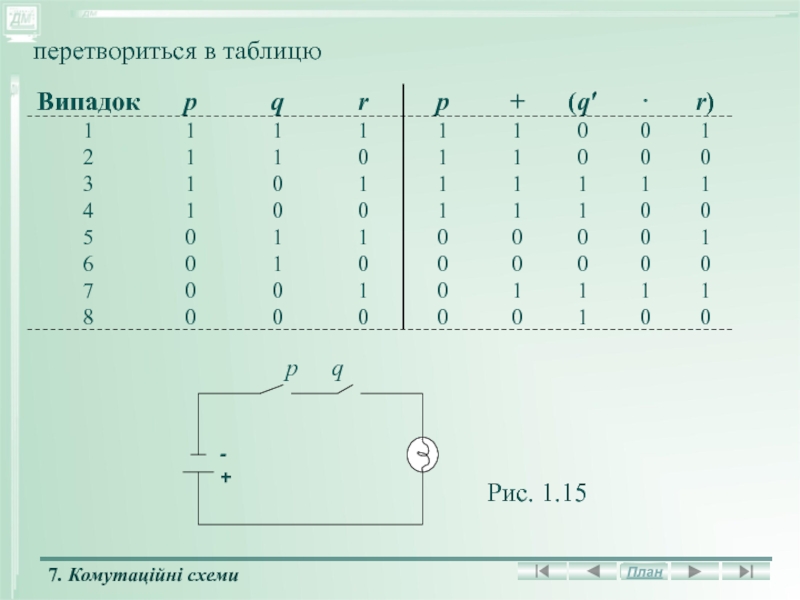
Слайд 51У таблицях істинності Т замінюється на 1, а F на
0, після чого таблиця істинності
Слайд 52перетвориться в таблицю
р q
-
+
Рис. 1.15
Слайд 53У 1938 р. Клод Шеннон помітив зв'язок між таблицями істинності
і електричними схемами. Розглянемо схему перемикання на рис. 1.15, яка
складається з джерела живлення (рис. 1.16) і електричної лампочки (рис. 1.17).
-
+
Привласнимо значення 1 перемикачам р і q, якщо вони замкнуті (тобто електричний струм проходить через них). У протилежній ситуації привласнимо їм значення 0. Привласнимо значення 1 схемі, коли лампочка світиться (тобто електричний струм через неї проходить). Помітимо, що при послідовному з'єднанні елементів ланцюга р і q, як це має місце на наведеній вище схемі, лампочка спалахує,
Рис. 1.16
Рис. 1.17
Слайд 54і значення схеми стає рівним 1 тільки у разі, коли
обидва перемикача замкнуті, тобто і р, і q мають значення
1. Таким чином, схема відповідає висловленню р q. Таке розташування перемикачів називається логічним елементом р і q, або схемою логічного множення. Цей логічний елемент позначається символом, зображеним на рис. 1.18.
р i q
q
Рис. 1.18
Тепер розглянемо схему перемикання, показану на рис. 1.19, де перемикачі р і q сполучені паралельно.
Слайд 55Рис. 1.19
Відзначимо, що тепер лампочка спалахує, і значення схеми стає
рівним 1, коли один з двох перемикачів р або q
замкнутий, тобто або значення р = 1, або q = 1 (або обидва вони рівні 1). Ця схема відповідає висловленню р + q. Таке розташування вимикачів називається логічним елементом
р або q, або схемою логічного додавання. Цей логічний елемент позначається символом, зображеним на рис. 1.20.
p або q
p
q
Рис.1.20
Слайд 56Припустимо, є схема, з одним перемикачем р, який має таку
властивість, що лампочка спалахує тоді і тільки тоді, коли р
розімкнений. Отже, схема має значення 1, коли р має значення 0, і має значення 0, коли р має значення 1. Ця схема відповідає р', а відповідний логічний елемент називається логічним елементом не, або інвертуванням. Логічний елемент не позначається символом, зображеним на рис. 1.21.
Рис. 1.21
p
не p
Слайд 57ПРИКЛАД 1.7. Схема на рис. 1.22 містить логічний елемент р
і q, за яким слідує інвертування, так що схема відповідає
виразу (р q)‘, тобто інвертування заперечує всю попередню йому схему.
ПРИКЛАД 1.8. Схема на рис. 1.23 містить з'єднання логічного елементу р або q з логічним елементом не r за допомогою логічної схеми множення.
Отже, вона відповідає виразу (p + q) r.
Слайд 58ПРИКЛАД 1.9. Булевий вираз, відповідний схемі на рис. 1.24, має
вигляд (p q) + (p r)
ПРИКЛАД 1.10. Комутаційна
схема, відповідна виразу
(р' q) + r, показана на рис. 1.25.