Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Таблицы сопряженности
Содержание
- 1. Таблицы сопряженности
- 2. Таким образом представленные данные не дают нам
- 3. Можно их сгруппировать в виде таблиц:по занятости:и по семейному положению:
- 4. А можно и по двум переменным сразу:Эта
- 5. Проценты в таблице сопряженности можно считать тремя способами: по столбцам, т.е. по независимой переменной
- 6. по строкам, т.е. по зависимой переменной
- 7. по всей таблице сразу:
- 8. ТАБЛИЦЫ СОПРЯЖЕННОСТИдля шкал наименованийдля шкал порядка
- 9. ТАБЛИЦЫ СОПРЯЖЕННОСТИдля шкал наименованийдля шкал порядка2 Пирсона,
- 10. ТАБЛИЦЫ СОПРЯЖЕННОСТИдля шкал наименованийдля шкал порядка
- 11. СТАТИСТИЧЕСКИЕ КРИТЕРИИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИПроверяют, есть ли
- 12. Слайд 12
- 13. 2 ПирсонаПример: мы хотим проверить, правда ли,
- 14. Было опрошено 550 человек.
- 15. Подсчет критерия 2 (Пирсона) -
- 16. Как определить теоретическую частоту?Для выделенной ячейки:Вероятность оказаться
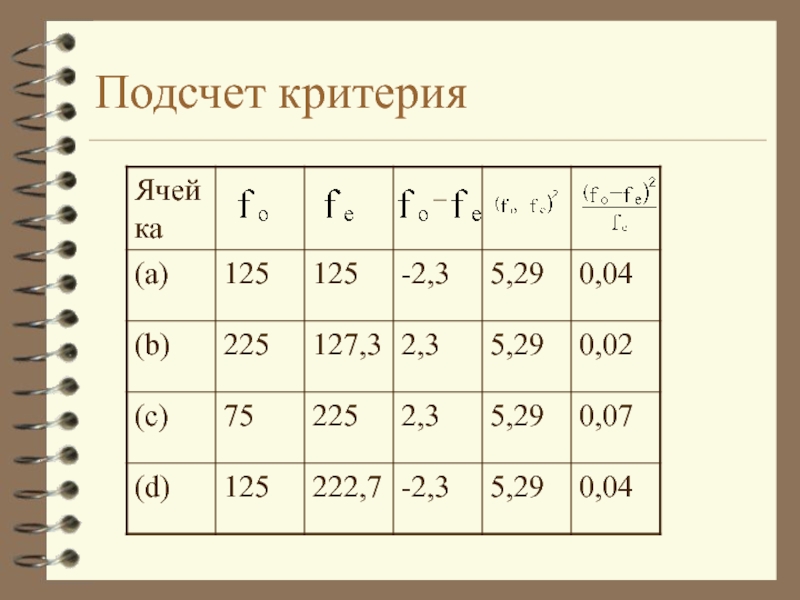
- 17. Подсчет критерия
- 18. Подсчитав таким образом теоретические частоты для всех
- 19. Ограничения критерия 2 Наблюдения должны быть
- 20. 2 МакНемараУвы! Только для таблиц 2*2.Тот критерий
- 21. Подсчет критерия 2 (МакНемара)Ограничения: A+D должно быть не меньше 10!
- 22. Пример: в телестудии проводятся дебаты, нужна ли
- 23. Что делать, если таблица большей размерности, а
- 24. Что делать, если таблица большей размерности, схема – интраиндивидуальная, а данные не дихотомические?Не проводить такие исследования!
- 25. МЕРЫ ЗАВИСИМОСТИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ
- 26. Меры зависимости для шкал наименованийВсе эти меры не имеют знака и не показывают направление отношений.
- 27. Коэффициент f употребляется в основном с
- 28. Коэффициент сопряженности С (или Ф) разработан для
- 29. V Крамера можно употреблять для любых
- 30. ТАБЛИЦЫ СОПРЯЖЕННОСТИдля шкал наименованийдля шкал порядка
- 31. В таблице сопряженности можно
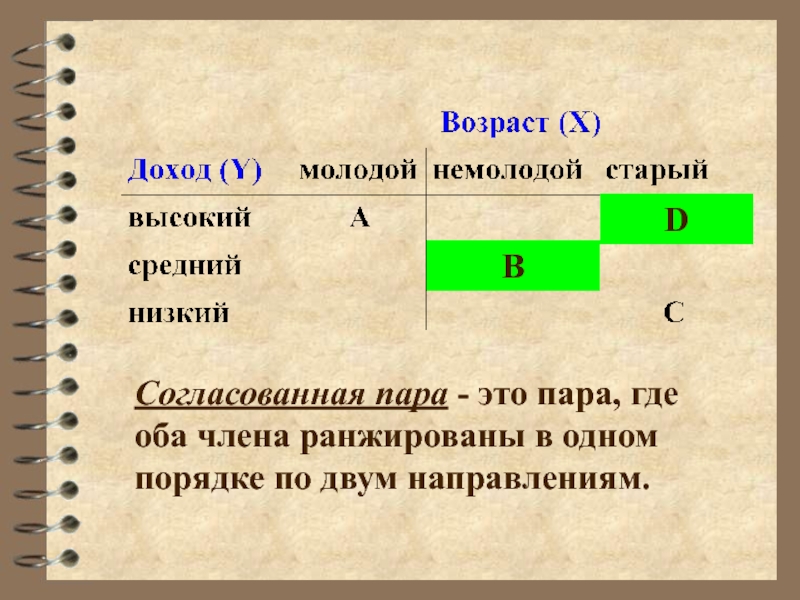
- 32. Согласованная пара - это пара, где оба члена ранжированы в одном порядке по двум направлениям.BD
- 33. Несогласованная пара - это пара, где оба члена ранжированы в противо-положном порядке по двум направлениям.BА
- 34. Связанная пара - это пара, где оба члена ранжированы одинаково по крайней мере по одному направлению.CD
- 35. Если в таблице преобладают несогласованные пары, то зависимость между переменными отрицательная.102030
- 36. Если в таблице преобладают согласованные пары, то зависимость между переменными положительная.102030
- 37. Меры зависимостиС- число согласованных пар,D - число
- 38. Меры зависимостидля шкал порядка имеют знак Кендалла всегда меньше 1, если таблица не квадратная
- 39. СПАСИБО ЗА ВНИМАНИЕ
- 40. Скачать презентанцию
Таким образом представленные данные не дают нам много информации.Проводим исследование: X – семейное положение – НП Y – занятость - ЗПСобранные данные выглядят примерно так:
Слайды и текст этой презентации
Слайд 2Таким образом представленные данные
не дают нам много информации.
Проводим исследование:
X
– семейное положение – НП Y – занятость - ЗП
выглядят примерно так:
Слайд 4А можно и по двум переменным сразу:
Эта замечательная таблица и
называется
таблицей сопряженности
По столбцам обычно приводится независимая переменная
По строкам обычно
идет зависимая переменная
Слайд 5Проценты в таблице сопряженности можно считать тремя способами:
по столбцам,
т.е. по независимой переменной
Слайд 9ТАБЛИЦЫ СОПРЯЖЕННОСТИ
для шкал наименований
для шкал порядка
2 Пирсона,
коэффициент сопряженности С,
V Крамера,
Ф
2 МакНемара,
для таблиц 2х2...
+
Кендалла,
Гамма (G),
Спирмена,
d Соммера
Слайд 11СТАТИСТИЧЕСКИЕ КРИТЕРИИ
ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ
Проверяют, есть ли зависимость в распределении
одной переменной от распределения по другой переменной.
Слайд 132 Пирсона
Пример: мы хотим проверить, правда ли,
что мужчины больше любят собак,
а женщины - кошек
Слайд 14 Было опрошено 550 человек. Результаты опроса
представлены в таблице:
Мы можем проверить, зависит ли предпочтение домашнего
животного (распределение по переменной Y) от пола
Слайд 15Подсчет критерия 2
(Пирсона)
- эмпирическая частота,
- теоретическая частота,
k=r*c,
r- число строк в таблице,
c –число столбцов
в таблице,df=(r-1)(c-1).
Слайд 16Как определить теоретическую частоту?
Для выделенной ячейки:
Вероятность оказаться мужчиной равна 200/550.
Вероятность
предпочитать собак равна 350/550.
Следовательно, вероятность быть мужчиной и предпочитать собак
равна(200/550 )*(350/550).
Умножив все это на количество испытуемых (550), получим теоретическую частоту для выделенной клетки:
(200/550 )*(350/550)*550=127,3.
Слайд 18Подсчитав таким образом теоретические частоты для всех клеток, находим
2=0,18
(это
эмпирическое значение)
Следовательно, предпочтение домашнего животного не зависит от пола:
мужчины и женщины одинаково любят собак.
Слайд 19Ограничения критерия 2
Наблюдения должны быть
независимы. Поэтому нельзя
использовать одного и того
же испытуемого несколькораз.
2 пропорционален размеру
выборки. Если увеличить
размер выборки в 2 раза, то и
значение 2 возрастет в 2 раза.
Поэтому не рекомендуется
применять 2 для больших
выборок.
Если теоретическая частота
клеток маленькая, то
вычисления могут быть не
точны. Сейчас общепринятым
является правило, что когда
df>1 теоретическая частота
должна быть равна или больше
5 по крайней мере в 80%
клеток.
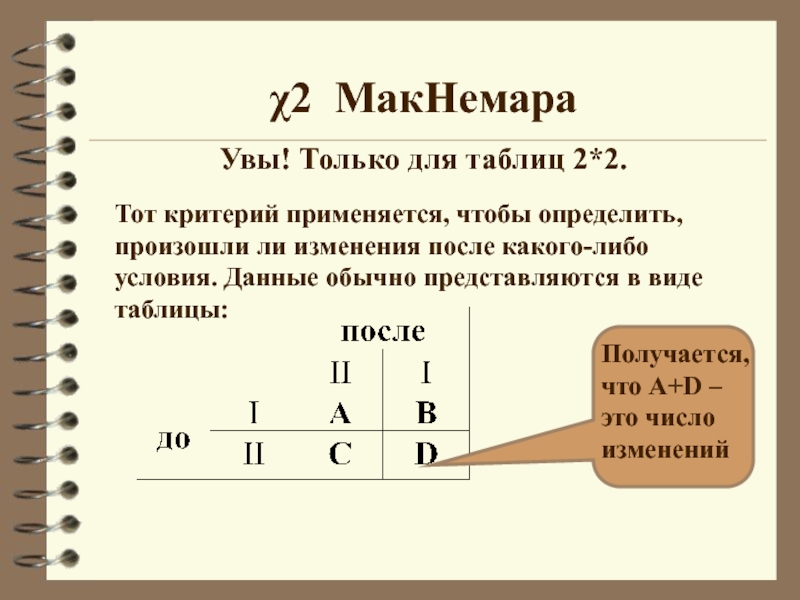
Слайд 202 МакНемара
Увы! Только для таблиц 2*2.
Тот критерий применяется, чтобы определить,
произошли ли изменения после какого-либо условия. Данные обычно представляются в
виде таблицы:Получается, что A+D – это число изменений
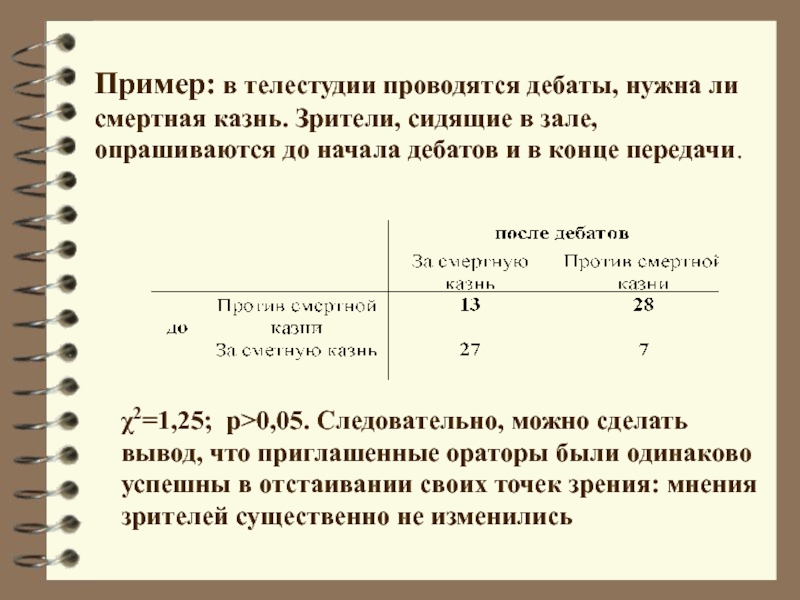
Слайд 22Пример: в телестудии проводятся дебаты, нужна ли смертная казнь. Зрители,
сидящие в зале, опрашиваются до начала дебатов и в конце
передачи.2=1,25; p>0,05. Следовательно, можно сделать вывод, что приглашенные ораторы были одинаково успешны в отстаивании своих точек зрения: мнения зрителей существенно не изменились
Слайд 23Что делать, если таблица большей размерности, а схема – интраиндивидуальная?
Для
случая, когда условий больше (до дебатов, после дебатов, через год
после дебатов…), можно использоватьQ-критерий Кочрена (Кохрена),
но только если данные представлены как дихотомические переменные
(да/нет, за/против,…)
Слайд 24Что делать, если таблица большей размерности, схема – интраиндивидуальная, а
данные не дихотомические?
Не проводить такие исследования!
Слайд 26Меры зависимости
для шкал наименований
Все эти меры не имеют знака
и не показывают направление отношений.
Слайд 27Коэффициент f
употребляется в основном с
таблицами 2х2
меняется от 0 (когда переменные
независимы) до 1 (когда они абсолютно зависимы)
Слайд 28Коэффициент сопряженности С (или Ф)
разработан для использования с квадратными
таблицами размера больше, чем 2х2
меняется
от 0 (когда переменные независимы) до , где k - число строк (столбцов)
Слайд 29V Крамера
можно употреблять для любых таблиц -
квадратных и прямоугольных
меняется от 0
(когда переменные независимы) до 1 (когда они абсолютно
зависимы)
где c – число строк,
r – число столбцов таблицы.
Слайд 31 В таблице сопряженности можно
представлять
и порядковые данные.
Обычно они перечисляются слева направо
(от меньшего к большему) и сверху вниз (от большего к меньшему):
Слайд 32Согласованная пара - это пара, где оба члена ранжированы в
одном порядке по двум направлениям.
B
D
Слайд 33Несогласованная пара - это пара, где оба члена ранжированы в
противо-положном порядке по двум направлениям.
B
А
Слайд 34Связанная пара - это пара, где оба члена ранжированы одинаково
по крайней мере по одному направлению.
C
D
Слайд 35Если в таблице преобладают несогласованные пары, то зависимость между переменными
отрицательная.
10
20
30
Слайд 36Если в таблице преобладают согласованные пары, то зависимость между переменными
положительная.
10
20
30
Слайд 37Меры зависимости
С- число согласованных пар,
D - число несогласованных пар,
Tx -
число пар, связанных по Х
Ty = число пар, связанных по
У
Слайд 38 Меры зависимости
для шкал порядка имеют знак
Кендалла всегда
меньше 1, если таблица не квадратная
