Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 12. Уравнения и неравенства
Содержание
- 1. Тема 12. Уравнения и неравенства
- 2. Тема 12. Уравнения и неравенства 12.1. Равносильность уравненийhttps://youtu.be/V9UOk7LWXAM
- 3. Два уравнения с одной переменной f(х) =
- 4. Пример 1. Выяснить, являются ли уравнения х2
- 5. Пример 2. Выяснить, являются ли уравнения х2
- 6. Решение. х2 + 3 = 0 –
- 7. Вывод:если два уравнения имеют одинаковые корни или не имеют корней, то такие уравнения – равносильные.
- 8. Если каждый корень уравнения f(x) = g(х)
- 9. Пример 4. Выяснить, какое из уравнений х
- 10. Пример 5. Выяснить, какое из уравнений х2
- 11. Запомните: если каждое из двух уравнений является следствием другого, то такие два уравнения равносильны.
- 12. Первый этап – технический. С помощью цепочки
- 13. Обычно при решении уравнений используются шесть теорем
- 14. Если какой-либо член уравнения перенести из одной
- 15. Если обе части уравнения возвести в одну
- 16. Показательное уравнение аf(x) = аg(x), где а
- 17. Следующие три теоремы называются «беспокойными». Их применение
- 18. Областью определения уравнения f(х) = g(х) или
- 19. Если обе части уравнения f(x) = g(х)
- 20. Решение. ОДЗ 2х – 1 ≥
- 21. Если обе части уравнения f(x) = g(х)
- 22. Решение. 6х – 11=(х – 1)2 ; х1
- 23. Пусть а > 0, a ≠ 1
- 24. Пример 8. Решить уравнение log7 (3х2+2) =
- 25. Тема 12. Уравнения и неравенства 12.2. Равносильность уравнений. Уравнение – следствиеhttps://youtu.be/5tNAKQ3KtZM
- 26. 1. Избавление от знаменателей, содержащих переменную величину.2.
- 27. Запомните: если в процессе решения уравнения произошло
- 28. Решение. Ответ: –2.Первый этап – технический. х2
- 29. Решение. Ответ: уравнение корней не имеет.Первый этап
- 30. Пример 6. Решить уравнение ln(х2 + 2х
- 31. Тема 12. Уравнения и неравенства 12.3. Равносильность уравнений Проверка корней. Потеря корней при решении уравненияhttps://youtu.be/zmh3ro09Amc
- 32. Второй этап – анализ решения. С помощью
- 33. ОДЗ: x = 4, x = 1; Ответ: 4.
- 34. Если при решении уравнения использовались равносильные преобразования,
- 35. Решение. ⇒ ⇒ Решением являетсяВозведем обе части уравнения в
- 36. Решение. Ответ: корней нет. ⇒ Решая ее, получаем, что
- 37. Решение. Ответ: 1. РешениеНайти ОДЗ в этом уравнении
- 38. РешениеНайдем ОДЗ уравнения. Для этого решим неравенство
- 39. Решение. Ответ: –6, 1. ++–
- 40. Алгоритм решения уравнения, записанного в виде f(х)h(х)
- 41. Пример 1. Решить уравнение x3 = х.Решение.
- 42. Сокращение обеих частей уравнения на множитель, содержащий неизвестное, может привести к потере корней.
- 43. Пример 2. Решить уравнение lg х2 =
- 44. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Пример 1. Выяснить, являются ли уравнения х2 – 1 =
0 и х –1 = 0 равносильными?
Решение.
х2 – 1
= 0;х1 = 1, х2 = –1;
х – 1 = 0;
х = 1;
Ответ: уравнения х2 – 1 = 0 и х – 1 = 0 не являются равносильными.
Вычислим корни уравнения х – 1 = 0.
Это уравнение имеет один корень — х = 1.
Решение
Вычислим корни уравнения х2 – 1 = 0.
Оно имеет два корня х1 = 1, х2 = –1
Данные уравнения не являются равносильными,
т.к. х2 – 1 = 0 имеет два корня, а уравнение х – 1 = 0 имеет один корень — х = 1
Слайд 5Пример 2. Выяснить, являются ли уравнения х2 – 9 =
0 и (х + 3)(2х – 8) = 0 равносильными?
Решение.
Ответ: уравнения х2 – 9 = 0 и (х + 3)(2х – 8) = 0 являются равносильными.
х2 – 9 = 0;
х1= 3, х2= –3;
(х + 3)(2х – 8) = 0;
х1= 3, х2= –3;
Данные уравнения являются равносильными,
так как каждое из них имеет по два корня: х1= 3, х2= –3
Слайд 6
Решение.
х2 + 3 = 0 – не имеет корней;
Данные уравнения являются равносильными, так как каждое из них не
имеет корней. Слайд 7Вывод:
если два уравнения
имеют одинаковые корни
или не имеют корней,
то такие уравнения – равносильные.
Слайд 8Если каждый корень уравнения f(x) = g(х) (1)
является в то
же время корнем уравнения р(х) = h(х) (2)
то уравнение (2)
называют следствием уравнения (1).Слайд 9Пример 4. Выяснить, какое из уравнений х – 2 =
0 и х2 – 5х + 6 = 0
является
следствием другого?Решение.
Ответ: уравнение х2 – 5х + 6 = 0 является следствием
уравнения х – 2 = 0.
х – 2 = 0;
х = 2;
х2 – 5х + 6 = 0;
х1 = 2; х2 = 3;
Решение
Обозначим уравнение х – 2 = 0 № 1, а уравнение х2 – 5х + 6 = 0 № 2.
Уравнение 1 имеет единственный корень, равный двум.
Уравнение 2 имеет два корня: х1 = 2; х2 = 3;
Единственный корень 1 уравнения — х = 2 — является также корнем второго.
Поэтому второе является следствием первого уравнения.
Слайд 10Пример 5. Выяснить, какое из уравнений х2 – 4х +
3 = 0 и х2 – 5х + 6 =
0является следствием другого?
Решение.
Ответ: ни одно из уравнений не является следствием другого.
х2 – 4х + 3 = 0;
х1=1; х2= 3;
х2 – 5х + 6 = 0;
х1 = 2; х2 = 3;
Решение
Обозначим уравнение х2 – 4х + 3 = 0 номером 1, а уравнение х2 – 5х + 6 = 0 — номером 2
Уравнение первое имеет два корня: х1=1; х2= 3,
Уравнение второе имеет два корня: х1 = 2; х2 = 3;
Оба уравнения имеют только по одному общему корню.
Согласно определению, ни одно из них не является следствием другого.
Слайд 11Запомните:
если каждое из двух уравнений является следствием другого, то
такие два уравнения равносильны.
Слайд 12Первый этап – технический.
С помощью цепочки преобразований
от исходного
уравнения
мы приходим к достаточно простому уравнению,
которое решаем и
находим корниАнализируем преобразования,
которые выполнили,
и выясняем, равносильны ли они.
Проверка всех найденных корней
их подстановкой в исходное уравнение обязательна при выполнении преобразований, которые могут привести к уравнению-следствию.
Этапы решения уравнения
Второй этап – анализ решения.
Третий этап – проверка.
Слайд 13Обычно при решении уравнений используются шесть теорем равносильности.
Первые три теоремы
называются «спокойными».
Их применение гарантирует равносильность преобразований без дополнительных условий.
Обычно их использование происходит автоматически, без особых размышлений.
Слайд 14Если какой-либо член уравнения перенести из одной части уравнения в
другую с противоположным знаком, то получится уравнение, равносильное данному уравнению.
Теорема
1. х5 + 3х2 – 7 = 4х + 10;
х5 + 3х2 – 4х = 17.
получаем уравнение, равносильное данному уравнению.
х5 + 3х2 - 4х = 10 + 7
переносим слагаемые 4х и – 7 из одной части в другую
Слайд 15Если обе части уравнения возвести в одну и ту же
нечетную степень, то получится уравнение, равносильное данному уравнению.
Теорема 2.
если
обе части уравнения возвести в пятую степень, то в силу теоремы второй, уравнения равносильны.
Слайд 16Показательное уравнение аf(x) = аg(x), где а > 0, a≠1,
равносильно уравнению f(x) = g(х).
Теорема 3.
Например, показательные уравнения
равносильны, т.к. основания равны,
следовательно уравнения равносильны
Слайд 17Следующие три теоремы называются «беспокойными». Их применение возможно при выполнении
определенных условий.
При их применении требуются внимание и аккуратность.
Слайд 18Областью определения уравнения f(х) = g(х) или областью допустимых значений
переменной (ОДЗ) называют множество тех значений переменной х, при которых
одновременно имеют смысл выражения f(х) и g(х).Слайд 19Если обе части уравнения f(x) = g(х) умножить на одно
и то же выражение h(х), которое:
1. имеет смысл всюду
в области определения (в области допустимых значений) уравнения f(x) = g(х); 2. нигде в этой области не обращается в 0;
то получится уравнение f(x)h(x) = g(x)h(x), равносильное данному в его ОДЗ.
Теорема 4.
Следствием теоремы четыре является еще одно «спокойное» утверждение: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Слайд 20
Решение.
ОДЗ 2х – 1 ≥ 0;
х + 3 ≠ 0;
х ≥
0,5;
Следствием теоремы четыре является еще одно «спокойное» утверждение: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
- умножим обе части уравнения на (х + 3)
Слайд 21Если обе части уравнения f(x) = g(х) неотрицательны в ОДЗ
уравнения, то после возведения обеих его частей в одну и
ту же четную степень n получится уравнение (f(x))n=(g(x))n равносильное данному в его ОДЗ.Теорема 5.
Слайд 22
Решение.
6х – 11=(х – 1)2 ;
х1 = 6, х2
= 2.
ОДЗ
Возведем в квадрат обе части уравнения и получим,
согласно теореме пятой, равносильное квадратное уравнение: ноль равен икс в квадрате минус восемь икс плюс двенадцать.
Корни х1 = 6, х2 = 2 также будут корнями исходного уравнения.
Решение
ОДЗ иррационального уравнения задается неравенством 6х – 11 ≥ 0,
решение которого х ≥ одной целой пяти шестым.
В этой ОДЗ обе части уравнения неотрицательны.
Слайд 23Пусть а > 0, a ≠ 1 и f(х) >
0, g(х) > 0,, то логарифмическое уравнение loga f(x) =
loga g(x) равносильно уравнениюf(x) = g(х).
Теорема 6.
Слайд 24Пример 8. Решить уравнение log7 (3х2+2) = log7 (4|х|+1).
Решение.
f(х)
= 3х2+2;
g(х)= 4|х|+1;
3х2 + 2 = 4|х| + 1;
В данном
логарифмическом уравнении функции f(х) = 3х2+2 и g(х)= 4|х|+1 принимают положительные значения при всех значениях переменной икс.
По теореме шесть, данное уравнение равносильно уравнению 3х2 + 2 = 4|х| + 1
Корни являются корнями исходного уравнения
Слайд 25Тема 12. Уравнения и неравенства
12.2. Равносильность уравнений. Уравнение –
следствие
https://youtu.be/5tNAKQ3KtZM
Слайд 261. Избавление от знаменателей, содержащих переменную величину.
2. Возведение обеих частей
уравнения в одну и ту же чётную степень.
3. Освобождение от
знаков логарифмов.Уравнение-следствие получается из данного уравнения путем расширения области определения уравнения.
Это возможно при выполнении таких преобразований, как
Слайд 27Запомните:
если в процессе решения уравнения произошло расширение области определения
уравнения, то обязательна проверка всех найденных корней.
Слайд 28
Решение.
Ответ: –2.
Первый этап – технический.
х2 – 3х –
10 = 0;
х1 = 5; х2 = –2.
Второй этап –
анализ решения. Проверка корней обязательна.
Третий этап – проверка.
Выполним цепочку преобразований, получим наиболее простое уравнение и решим его. Для этого умножим обе части уравнения на общий знаменатель дробей, то есть на выражение икс умноженное на икс минус пять.
Проверим выполненные преобразования на равносильность.
При решении уравнения, мы его обе части умножили на выражение, содержащее переменную. Значит, область определения уравнения расширилась. Поэтому проверка корней обязательна.
Подставим найденные корни в исходное уравнение.
При икс равном минус два общий знаменатель не обращается в нуль. Значит, икс равно минус два является корнем данного уравнения.
При икс равном пяти общий знаменатель обращается в нуль. Поэтому икс равно пяти – посторонний корень.
Слайд 29
Решение.
Ответ: уравнение корней не имеет.
Первый этап – технический.
х
– 6 = 4 – х;
2х = 10;
х = 5.
Второй
этап – анализ решения. Проверка корней обязательна.
Третий этап – проверка.
Первый этап — технический.
Для того чтобы получить простое уравнение и решить его, выполним цепочку преобразований.
Возведем в квадрат (четная степень) обе части этого уравнения, перенесем иксы в левую часть , а числа в правую часть уравнения, приведем подобные слагаемые, получим: 2х = 10. х = 5.
Второй этап – анализ решения.
Проверим выполненные преобразования на равносильность.
При решении уравнения, мы его обе части возвели в квадрат. Значит, область определения уравнения расширилась. Поэтому проверка корней обязательна.
Третий этап – проверка.
Подставим найденные корни в исходное уравнение.
Если икс равен пяти, выражение квадратный корень из четырех минус икс не определено, поэтому икс, равный пяти – посторонний корень. Значит, данное уравнение не имеет корней
Слайд 30Пример 6. Решить уравнение ln(х2 + 2х – 7) =
ln(х – 1).
Решение.
Ответ: 2.
Первый этап – технический.
х2 +
2х – 7= х – 1;х2 + х – 6 = 0;
х1 = 2, х2 = –3.
Второй этап – анализ решения.
Проверка корней обязательна.
Третий этап – проверка.
х = 2: ln1= ln1;
х = –3: ln(х2 + 2х – 7),
ln(х – 1) – не определены;
Первый этап — технический.
Выполним цепочку преобразований, получим наиболее простое уравнение и решим его. Для этого потенцируем
уравнение, перенесем все слагаемые в левую часть уравнения, приведем подобные члены, получим квадратное уравнение икс квадрат плюс икс минус шесть равно нулю.
Вычислим корни: х1 = 2, х2 = –3.
Второй этап – анализ решения.
Проверим выполненные преобразования на равносильность.
В процессе решения данного уравнения мы освободились от знаков логарифмов. Значит, область определения уравнения расширилась. Поэтому проверка корней обязательна.
Третий этап – проверка.
Подставим найденные корни в исходное уравнение.
Если икс равен двум, то получаем натуральный логарифм единицы равен натуральному логарифму единицы —
верное равенство.
Значит, икс равный двум – корень данного уравнения.
Если икс равен минус трем, то натуральный логарифм выражения икс квадрат плюс два икс минус семь и натуральный логарифм выражения икс минус один не определены. Значит, икс равный минус трем — посторонний корень.
Слайд 31Тема 12. Уравнения и неравенства
12.3. Равносильность уравнений
Проверка корней.
Потеря корней при решении уравнения
https://youtu.be/zmh3ro09Amc
Слайд 32Второй этап – анализ решения.
С помощью цепочки преобразований от
исходного уравнения мы приходим к достаточно простому, которое решаем и
находим корни.Анализируем преобразования, которые выполнили, и выясняем, равносильны ли они
Проверка всех найденных корней их подстановкой в исходное уравнение обязательна при выполнении преобразований, которые могут привести к уравнению-следствию
Вопрос - Всегда ли нужно выделять три этапа при решении уравнения?
Ответ - Конечно, нет. Обязательно проводить анализ на равносильность преобразований
Первый этап – технический.
Третий этап – проверка.
Слайд 34Если при решении уравнения использовались равносильные преобразования, то проверка не
требуется.
При проверке корней уравнения очень часто используют ОДЗ.
Если
по ОДЗ проверку сделать трудно, то выполняют ее подстановкой в исходное уравнение.Слайд 35
Решение.
⇒
⇒
Решением является
Возведем обе части уравнения в квадрат,
перенесем слагаемые
из одной части уравнения в другую,
приведем подобные слагаемые, получим
квадратное уравнениеПроверка
Значение х1=√2 является корнем уравнения, так как оно входит в ОДЗ.
Значение х2= -√2 не является корнем уравнения, т.к. оно не входит в ОДЗ.
Проверим х=√2 , подставив его в исходное равенство, получим верное равенство,
значит, х=√2 является корнем уравнения.
ОДЗ уравнения определяется системой двух неравенств:
Корни квадратного уравнения
Слайд 36
Решение.
Ответ: корней нет.
⇒
Решая ее, получаем, что эта система не
имеет решений.
Корнем уравнения не может быть ни одно из
значений переменной икс. ОДЗ иррационального уравнения переделяется системой двух неравенств:
Слайд 37
Решение.
Ответ: 1.
Решение
Найти ОДЗ в этом уравнении довольно трудно.
Выполним преобразования:
возведем обе части этого уравнения в квадрат,
перенесем все слагаемые
в левую часть уравнения и приведем подобные слагаемые, два корня запишем под один, получим подобные радикалы, приводим подобные, делим на коэффициент минус 12, и раскладываем подкоренное выражение на множители, получим уравнение в виде произведения двух множителей, равное нулю. Решив его, найдем корни: икс первое равно единице, икс второе равно нулю.
Так как мы обе части уравнения возводили в четную степень, то проверка корней обязательна.
Проверка
Если икс равен единице, то получим верное равенство, значит, икс равный единице – корень уравнения.
Если икс равен нулю, то квадратный корень из минус единицы не определен.
Значит, икс равный нулю – посторонний корень.
Слайд 38
Решение
Найдем ОДЗ уравнения.
Для этого решим неравенство икс квадрат плюс
пять икс плюс два больше нуля.
Решаем неравенство методом интервалов. Для
этого разложим его левую часть на множители, предварительно решив квадратное уравнение, и учитывая знак неравенства, определяем ОДЗ. ОДЗ равно объединению открытых лучей от минус бесконечности до минус дроби пять плюс квадратный корень из семнадцати, деленное на два, и от минус дроби пять минус квадратный корень из семнадцати, деленное на два, до плюс бесконечности. Теперь приступим к поиску корней уравнения.
Учитывая, что три равно логарифму восьми по основанию два, запишем уравнение в следующем виде: логарифм выражения икс квадрат плюс пять икс плюс два по основанию два равно логарифму восьми по основанию два. Потенцируем уравнение, получим и решим квадратное уравнение.
Дискриминант равен сорока девяти.
Вычисляем корни:
икс первое равно минус шести; икс второе равно единице.
Проверка
Минус шесть принадлежит ОДЗ, единица принадлежит ОДЗ, значит, оба числа являются корнями уравнения.
Слайд 40Алгоритм решения уравнения, записанного в виде f(х)h(х) = g(х) h(х):
разложить
на множители g(х)[f(х) – g(х)] = 0;
получить два уравнения h(х)=0;
f(х) – g(х) = 0;вычислить корни.
Слайд 41Пример 1. Решить уравнение x3 = х.
Решение.
1 способ.
х2 =
1;
х1 = 1, х2 = –1.
2 способ.
х3 – х =
0;х(х2 – 1) = 0;
х1=0, х2=1, х3= –1.
При решении 1 способом мы потеряли один корень, х = 0.
Слайд 42Сокращение обеих частей уравнения на множитель, содержащий неизвестное, может привести
к потере корней.
Слайд 43Пример 2. Решить уравнение lg х2 = 2.
Решение.
1 способ.
х2
= 100;
х1 = 10, х2= –10.
2 способ.
2 lg х =
2;lg х = 1;
х = 10.
lg х2 = 2 lg |х|
































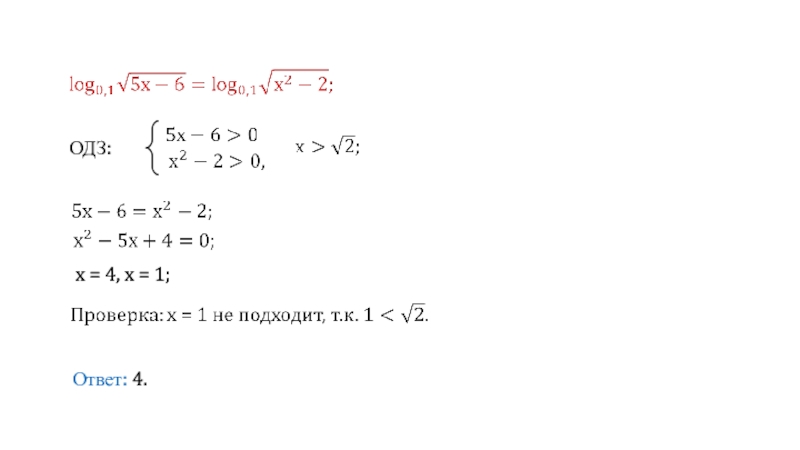






![Тема 12. Уравнения и неравенства Алгоритм решения уравнения, записанного в виде f(х)h(х) = g(х) h(х):разложить на Алгоритм решения уравнения, записанного в виде f(х)h(х) = g(х) h(х):разложить на множители g(х)[f(х) – g(х)] = 0;получить](/img/tmb/7/619927/e479fded429d1325e16796ecca797892-800x.jpg)






















