Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 2. Обработка результатов измерений
Содержание
- 1. Тема 2. Обработка результатов измерений
- 2. 2.1. Погрешность – характеристика результатов измеренийПонятия:«Точность
- 3. Результат измерений – это значение физической величины,
- 4. Погрешность измерения
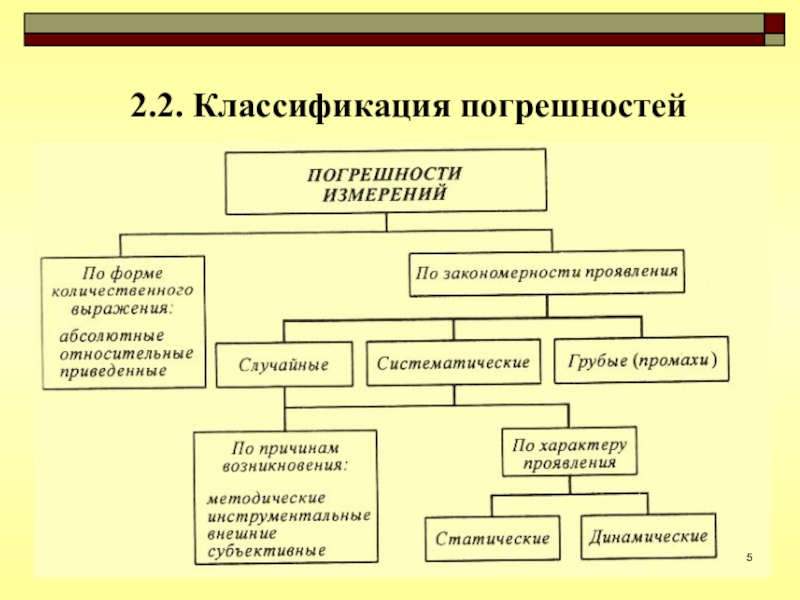
- 5. 2.2. Классификация погрешностей
- 6. 2.3. Анализ случайных погрешностейСлучайные погрешности – составляющие
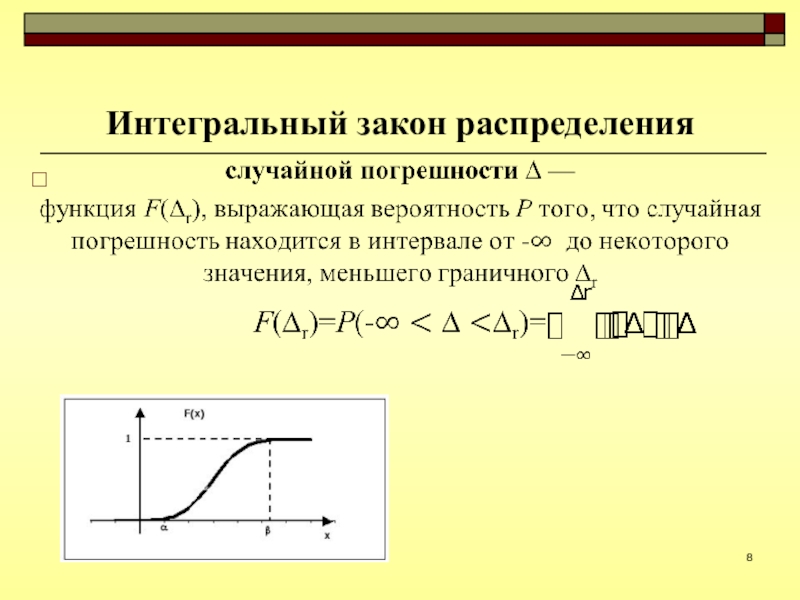
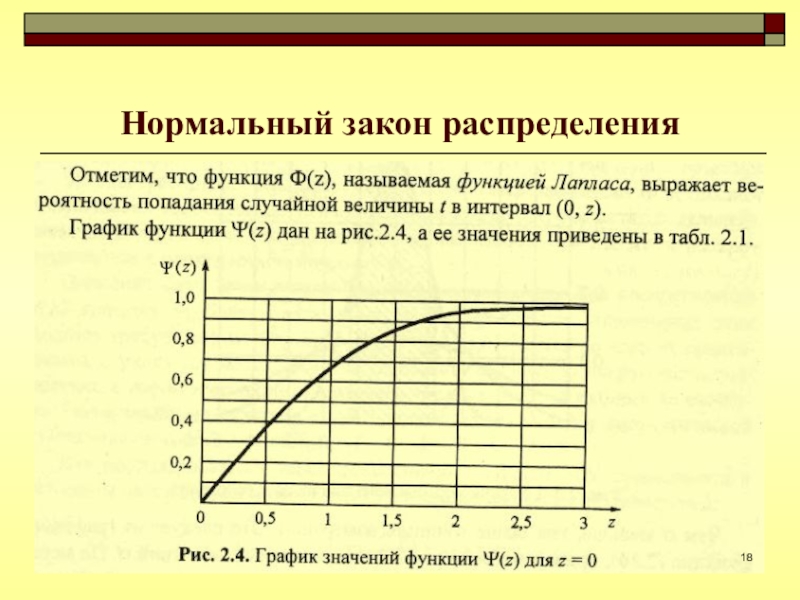
- 7. Закон распределения -наиболее общая характеристика случайной величиныИспользуют две формы описания этого закона:интегральная, дифференциальная
- 8. Интегральный закон распределения
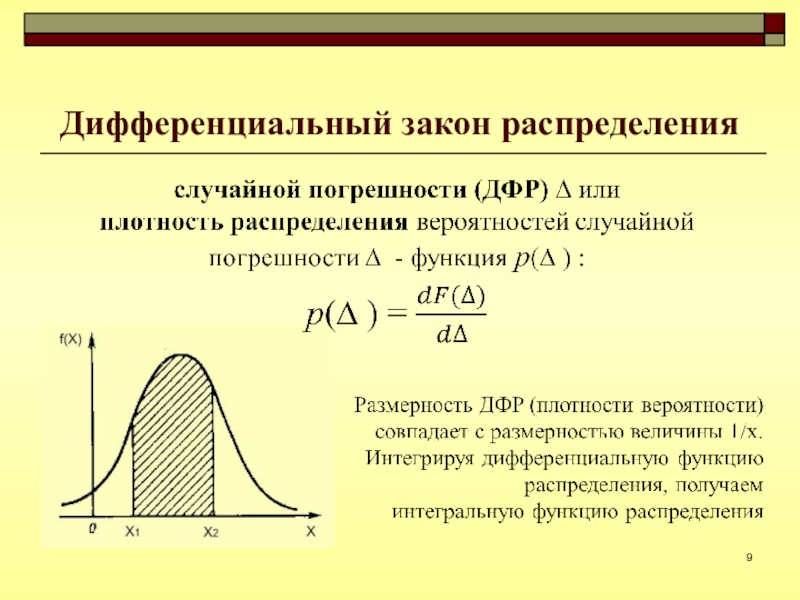
- 9. Дифференциальный закон распределения
- 10. Практический интерес – поиск вероятности, с
- 11. Числовые характеристики законов распределения – начальные и
- 12. Математическое ожиданиеНаиболее важным является начальный момент первого
- 13. Дисперсия и среднеквадратическое отклонение
- 14. 2.3. Законы распределения случайных величиннормальный (Гаусса)равномерныйтрапецеидальныйтреугольный (Симпсона)Стьюдента
- 15. Нормальный закон распределения
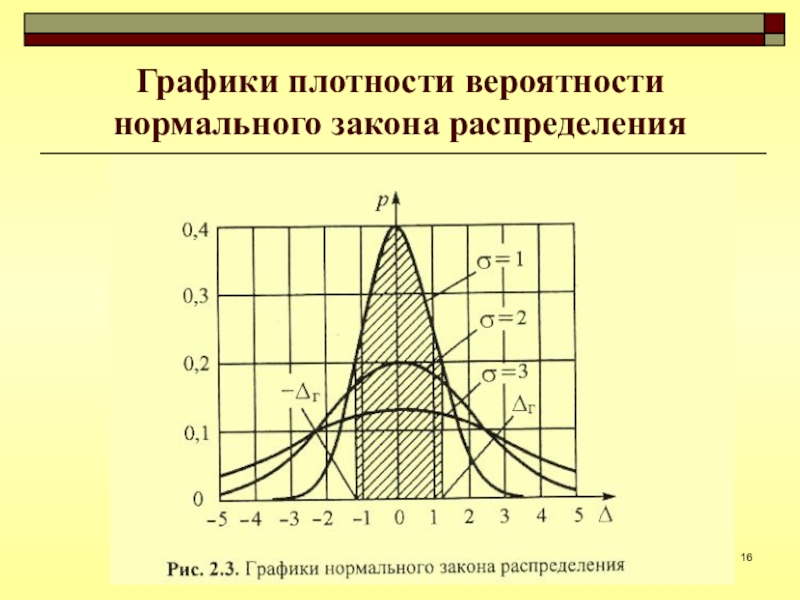
- 16. Графики плотности вероятности нормального закона распределения
- 17. Нормальный закон распределения
- 18. Нормальный закон распределения
- 19. Нормальный закон распределения погрешностей
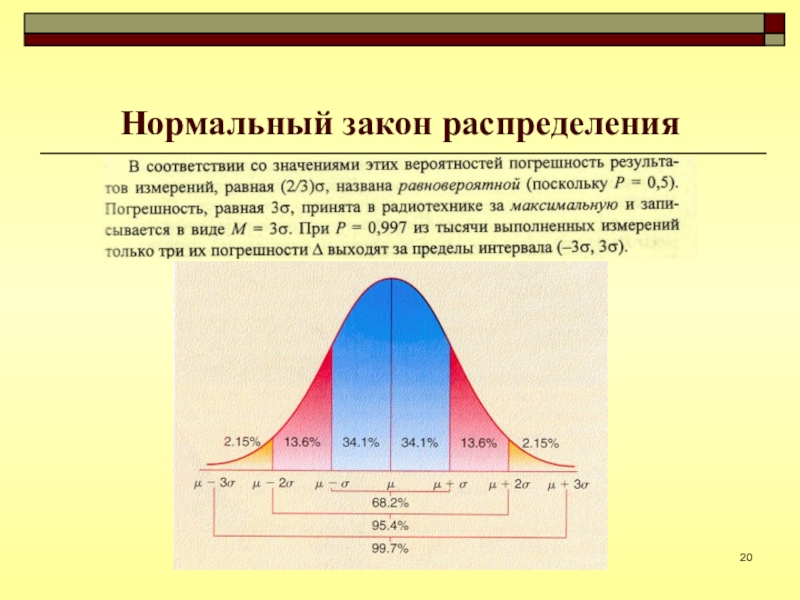
- 20. Нормальный закон распределения
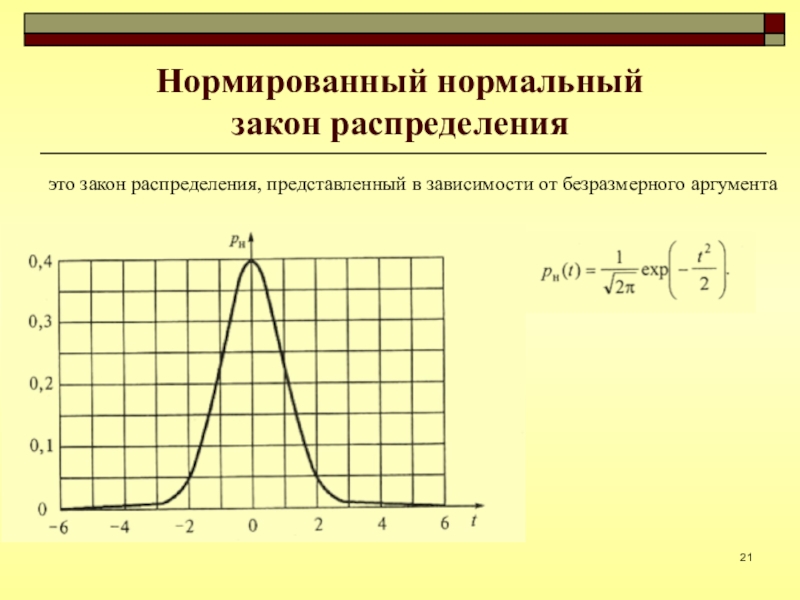
- 21. Нормированный нормальный закон распределенияэто закон распределения, представленный в зависимости от безразмерного аргумента
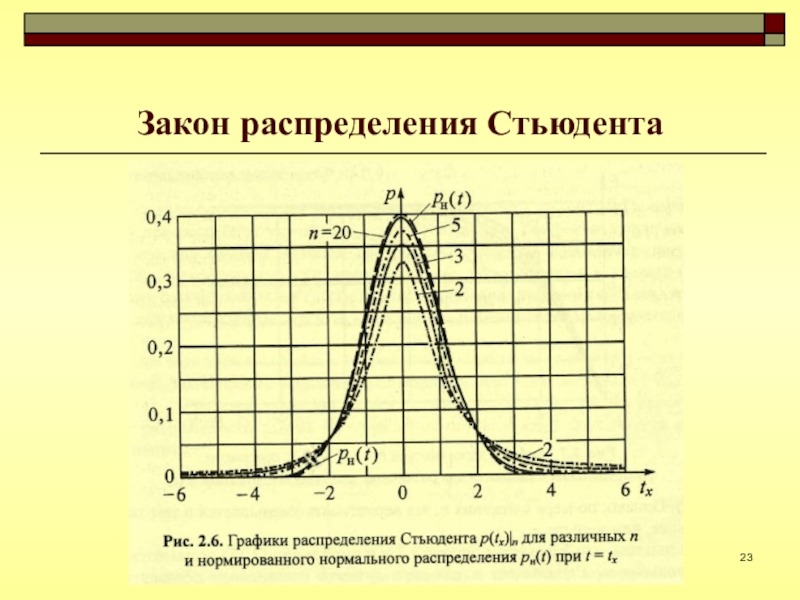
- 22. Закон распределения СтьюдентаПрименяется в процессе обработки результатов
- 23. Закон распределения Стьюдента
- 24. Закон распределения СтьюдентаПараметр tr - коэффициент
- 25. Равномерный закон распределения
- 26. Треугольный закон распределения
- 27. Доверительная вероятность и доверительный интервал
- 28. Скачать презентанцию
2.1. Погрешность – характеристика результатов измеренийПонятия:«Точность измерения» и «Погрешность измерения»Точность измерения - качество измерения, отражающее близость результата измерения к истинному значению измеряемой величиныПогрешность измерения – мера близости измеренного значения к
Слайды и текст этой презентации
Слайд 1Тема 2.
Обработка результатов измерений
2.1. Погрешность — характеристика результата измерений
2.2. Классификация
погрешностей
Слайд 22.1. Погрешность –
характеристика результатов измерений
Понятия:
«Точность измерения» и «Погрешность измерения»
Точность
измерения - качество измерения, отражающее близость результата измерения к истинному
значению измеряемой величиныПогрешность измерения – мера близости измеренного значения к истинному
Слайд 3Результат измерений – это значение физической величины, полученное в результате
измерений.
Проведение многократных измерений в одинаковых условиях приводит к результатам, отличающимся
друг от друга.Измерение можно считать законченным, если найден не только результат измерения, но и проведена оценка его погрешности.
Результат измерения и его погрешность рассматриваются как случайные величины
Слайд 62.3. Анализ случайных погрешностей
Случайные погрешности –
составляющие погрешности измерений, изменяющиеся
случайным образом
по значению и знаку
при повторных измерениях
в
одних и тех же условияхКоличественная характеристика случайного события –
его вероятность Р –
отношение числа положительных исходов события
к общему числу событий.
Слайд 7Закон распределения -
наиболее общая характеристика
случайной величины
Используют две формы описания
этого закона:
интегральная,
дифференциальная
Слайд 10Практический интерес – поиск вероятности, с которой погрешность находится в
заданном интервале
На интервале всех возможных значений погрешностей
Слайд 11Числовые характеристики законов распределения – начальные и центральные моменты
Для описания
отдельных свойств случайной величины х
используются числовые характеристики законов распределения
p(x) - начальные и центральные моменты k-го порядка, представляющие собой некоторые средние значения.
Моменты
называются начальными,
если с их помощью усредняются величины, отсчитываемые от начала координат,
называются центральными,
если усредняются величины,
отсчитываемые от центра распределения.