Слайд 1Тема 2
Элементы математической логики
Слайд 2Высказывания
Предложение, о котором имеет смысл говорить, что оно является истинным
или ложным, называют высказыванием.
Являются ли высказываниями предложения?
Волга впадает в Черное
море.
2+2=4
Который час?
Мойте руки перед едой!
Земля – единственная обитаемая планета во Вселенной.
Слайд 3Значение истинности высказывания
Слайд 4Элементарные и сложные высказывания
Если никакая часть высказывания сама по себе
не является высказыванием, то высказывание называют элементарным или исходным.
Сложным называют
высказывание, допускающее разделение его на другие высказывания.
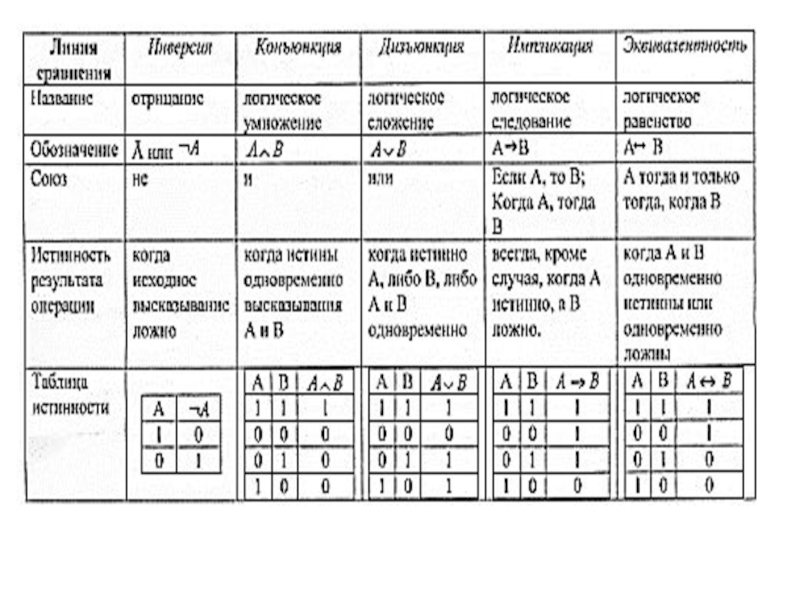
Слайд 5Операции над высказываниями
1. Инверсия ( логическое отрицание)
2. Дизъюнкция (логическое
сложение)
3. Конъюнкция (логическое умножение)
4. Импликация (логическое следствие)
5. Эквивалентность (логическое равенство)
Слайд 8Основные законы логики
1. Закон тождества
2. Закон непротиворечия
3. Закон исключения третьего
4.
Закон отрицания отрицания
Слайд 9Закон тождества
Всякое высказывание тождественно самому себе:
А = А
Слайд 13Пример задачи
Трое подозреваемых в преступлении Иванов, Петров и Сидоров дали
следующие показания:
Иванов сказал: «Если виновен Сидоров, то и Петров
тоже виновен».
Петров сказал: «Виновен либо Иванов, либо Сидоров, но не оба».
Сидоров сказал: «Я не виновен, а виновен Петров».
Слайд 14Построить таблицу истинности каждого высказывания и по ней определить:
а)
Кто виновен, если все говорят правду?
б) Кто виновен, если
все лгут? в) Кто лжет, если все виновны?
г) Кто лжет, если все невиновны?
д) Кто виновен, если виновные лгут, а невиновные говорят правду?
Слайд 15Введем простые высказывания: А={виновен Иванов};
В={виновен Петров};
С={виновен Сидоров}.
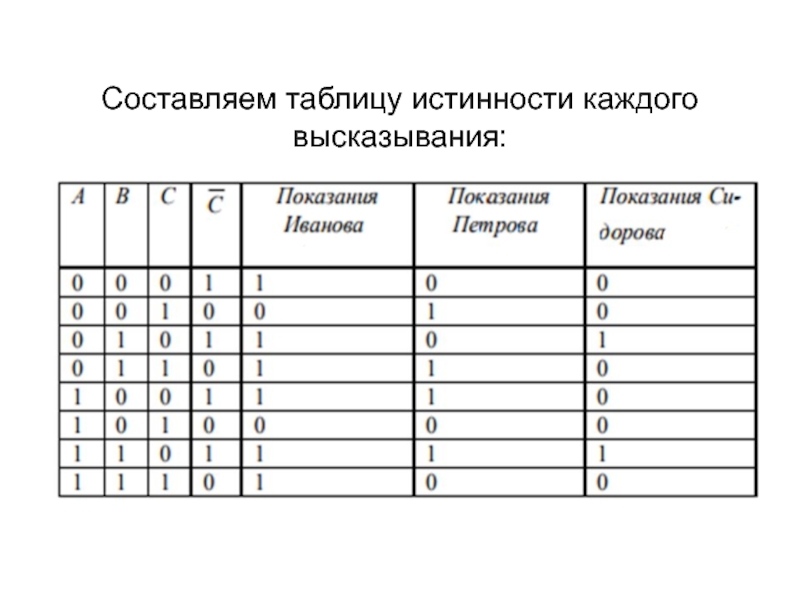
Слайд 17Составляем таблицу истинности каждого высказывания:
Слайд 18а) Если все говорят правду, то в показаниях (последние три
столбца) должны быть три единицы. Такому условию соответствует предпоследняя строка,
из которой по значениям в первых трех столбцах (1,1,0) делаем вывод, что Иванов и Петров виновны, а Сидоров нет.
Слайд 19б) Если все лгут, то в показаниях должны быть три
нуля. Такому условию соответствует шестая строка, из которой по значениям
в первых трех столбцах делаем вывод, что Иванов и Сидоров виновны, а Петров нет.
Слайд 20в) Условию того, что все виновны, соответствует последняя строка, у
которой в первых трех столбцах все единицы. По значениям показаний
(последние три столбца) видно, что Иванов говорит правду, а Петров и Сидоров лгут
Слайд 21г) Условию того, что все невиновны, соответствует первая строка, у
которой в первых трех столбцах все нули. По значениям показаний
видно, что Иванов говорит правду, а Петров и Сидоров лгут.
Слайд 22д) Если виновные лгут, а невиновные говорят правду, то в
каждой паре значений столбцов виновности (первые три) и показаний (последние
три) для каждого подозреваемого должны стоять разные значения. Этому условию соответствует третья строка у которой значения первых трех столбцов (0,1,0), а последних трех (1,0,1). Это означает, что Иванов невиновен и говорит правду, Петров виновен и лжет, а Сидоров невиновен и говорит правду.