Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 3 Теорема Остроградского – Гаусса дискретного и непрерывного распределения
Содержание
- 1. Тема 3 Теорема Остроградского – Гаусса дискретного и непрерывного распределения
- 2. 3.1. Основные определения.3.2. Теорема Остроградского – Гаусса
- 3. если 3.1. Основные определения1. Линейная плотность заряда
- 4. .2. Поверхностная плотность заряда – это физическая
- 5. 3. Объемная плотность заряда ρ –
- 6. — стационарное поле поток через замкнутую поверхность К оглавлениюгде — единичная нормаль к поверхности S. Рис.3.4.(3.7)(3.8)(3.9)-
- 7. 3.2. Теорема Остроградского-Гаусса Пусть имеется уединенный точечный
- 8. . Поток вектора напряженности равен величине
- 9. Поэтому можно сказать, что поток вектора напряженности
- 10. .В случаях, если имеется непрерывное распределение зарядов
- 11. 3.3. Применение теоремы Остроградского – Гаусса3.3.1. Поле
- 12. т.к. проекция вектора на нормаль к боковой поверхности равна нулю, тоК оглавлению(3.14)
- 13. 3.3.2. Поле разноименных плоскостей Применим принцип суперпозиции:К оглавлениюРис.3.9. Поле разноименных плоскостей Рис.3.10.(3.15)
- 14. 3.3.3. Поле заряженной нити. К оглавлениюРис.3.11. Поле заряженной нити(3.16)
- 15. 3.3.4. Поле заряженной сферы. Поле внутри сферы. Рис.3.12. Поле внутри сферы. (3.17)
- 16. Поле вне сферыТ. к. , то Если К оглавлениюРис.3.13. Поле вне сферы(3.18)(3.19)(3.20)
- 17. 3.3.5. Поле заряженного шараПоле внутри шара.Рис.3.14. Поле внутри шара.(3.21)
- 18. Поле вне шара.- обратно квадратичная зависимость.К оглавлениюРис.3.15. Поле вне шара(3.22)
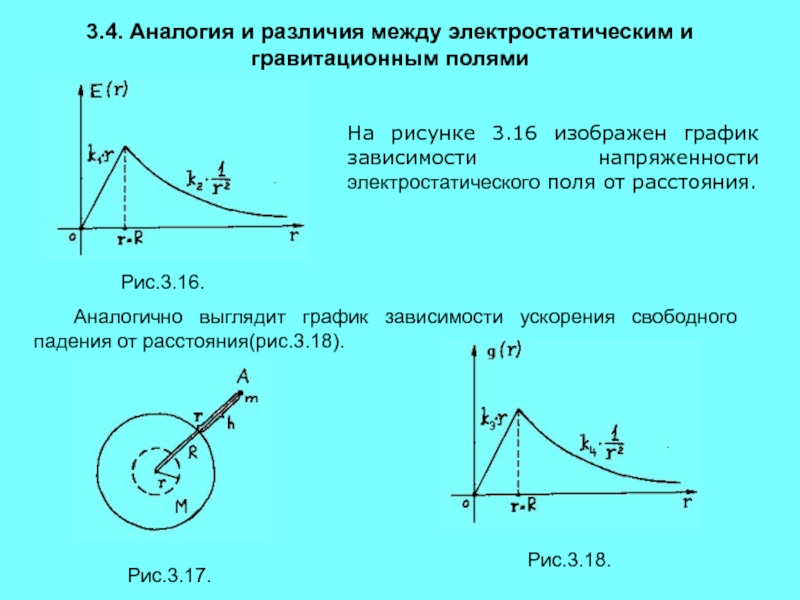
- 19. 3.4. Аналогия и различия между электростатическим и
- 20. Как вы считаете: случайно ли это совпадение?К оглавлению(3.23)(3.24)
- 21. Скачать презентанцию
3.1. Основные определения.3.2. Теорема Остроградского – Гаусса для дискретного и непрерывного распределения зарядов.3.3. Применение теоремы Остроградского – Гаусса для случаев:3.3.1. Заряженная плоскость.3.3.2. Две разноименно заряженные плоскости.3.3.3. Заряженная нить.3.3.4. Заряженная сфера.3.3.5. Заряженный
Слайды и текст этой презентации
Слайд 1Тема 3
Теорема Остроградского – Гаусса дискретного и непрерывного распределения зарядов
и ее применение
Слайд 23.1. Основные определения.
3.2. Теорема Остроградского – Гаусса для дискретного и
непрерывного распределения зарядов.
3.3. Применение теоремы Остроградского – Гаусса для случаев:
3.3.1.
Заряженная плоскость.3.3.2. Две разноименно заряженные плоскости.
3.3.3. Заряженная нить.
3.3.4. Заряженная сфера.
3.3.5. Заряженный шар.
3.4. Аналогия между электростатическим и гравитационным полями.
оглавление
Слайд 3если
3.1. Основные определения
1. Линейная плотность заряда
— это физическая
величина,
численно равная заряду, приходящемуся на единицу длины.
Рис.3.1. Линейная
плотность заряда (3.1)
(3.2)
то
Слайд 4.
2. Поверхностная плотность заряда
– это физическая величина,
численно равная
заряду, приходящемуся на единицу площади.
Рис.3.2. Поверхностная плотность заряда
(3.3)
(3.4)
,
если
Слайд 5
3. Объемная плотность заряда ρ – это физическая величина,
численно равная заряду, заключенному в единице объема
Рис.3.3. Объемная плотность заряда
(3.5)
(3.6)
,
если
Слайд 6— стационарное поле
поток через замкнутую поверхность
К оглавлению
где
— единичная нормаль к поверхности S.
Рис.3.4.
(3.7)
(3.8)
(3.9)
-
Слайд 73.2. Теорема Остроградского-Гаусса
Пусть имеется уединенный точечный заряд. Рассчитаем поток
вектора этого заряда через замкнутую поверхность, окружающую этот заряд.
Сфера.
Рис.3.5.Сфера
(3.10)
Слайд 8
.
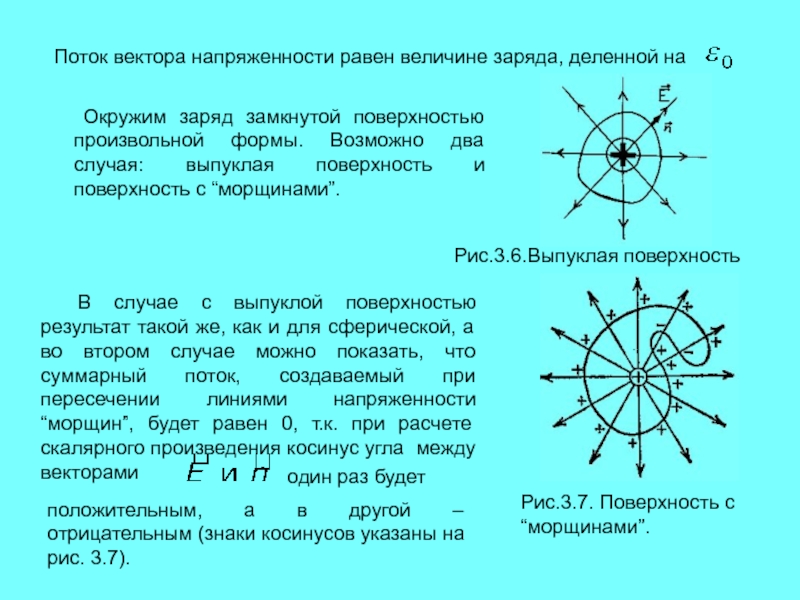
Поток вектора напряженности равен величине заряда, деленной на
Окружим заряд замкнутой поверхностью произвольной формы. Возможно два случая:
выпуклая поверхность и поверхность с “морщинами”.Рис.3.6.Выпуклая поверхность
В случае с выпуклой поверхностью результат такой же, как и для сферической, а во втором случае можно показать, что суммарный поток, создаваемый при пересечении линиями напряженности “морщин”, будет равен 0, т.к. при расчете скалярного произведения косинус угла между векторами
один раз будет
положительным, а в другой – отрицательным (знаки косинусов указаны на рис. 3.7).
Рис.3.7. Поверхность с “морщинами”.
Слайд 9Поэтому можно сказать, что поток вектора напряженности поля точечного заряда
через произвольно замкнутую поверхность, окружающую этот заряд, равен величине этого
заряда, деленной наПусть имеется система k точечных уединенных зарядов
Воспользуемся принципом суперпозиции.
(3.11)
Слайд 10.
В случаях, если имеется непрерывное распределение зарядов в некоторых телах,
необходимо от операции суммирования перейти к операции интегрирования. Тогда получим:
заряженная
линиязаряженная плоскость
Заряженное тело
К оглавлению
Поток вектора напряженности системы k точечных неподвижных зарядов в вакууме равен алгебраической сумме этих зарядов деленной на
(3.12.)
Теорема Остроградского-Гаусса в интегральной форме
(3.13)
Слайд 113.3. Применение теоремы Остроградского – Гаусса
3.3.1. Поле заряженной плоскости
1.
Линии напряженности перпендикулярны плоскости.
2. Их густота одинакова
в каждой точке
одинаково. Так как плоскость бесконечна, то исходя из соображений симметрии значение модуля
Рис.3.8. Поле заряженной плоскости
Слайд 133.3.2. Поле разноименных плоскостей
Применим принцип суперпозиции:
К оглавлению
Рис.3.9. Поле разноименных
плоскостей
Рис.3.10.
(3.15)
Слайд 193.4. Аналогия и различия между электростатическим и гравитационным полями
Аналогично выглядит
график зависимости ускорения свободного падения от расстояния(рис.3.18).
Рис.3.16.
Рис.3.17.
Рис.3.18.
На рисунке 3.16 изображен
график зависимости напряженности электростатического поля от расстояния.
