Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема №2 Задача 1 Задача 4 Задача 2 Задача 3 Задача 5 Задача 6 Задача 7 Задача
Содержание
- 1. Тема №2 Задача 1 Задача 4 Задача 2 Задача 3 Задача 5 Задача 6 Задача 7 Задача
- 2. ПотенциалРазность потенциалов между двумя точками электрического поля
- 3. 3) Цилиндрический конденсаторРазность потенциалов между внутренним цилиндром
- 4. Шарик массой m=40 мг, заряженный положительным зарядом
- 5. Дано:r – ? Решение:W2=0выразим r где 1
- 6. На какое расстояние могут сблизиться два электрона,
- 7. Ответ: два электрона, летящие с относительной скоростью
- 8. Два шарика с зарядами q1=6,6нКл и q2=13,3
- 9. Дано:Решение:А – ? ПолучимВторой способПервый способ
- 10. Какая работа А совершается при перенесении точечного
- 11. Дано:Решение:А – ? где S – площадь
- 12. На расстоянии r1=4см от бесконечно длинной заряженной
- 13. Дано:Решение: – ? q = 0,6610-9
- 14. Разность потенциалов между пластинами плоского конденсатора U=90В.
- 15. U = 90 ВS = 6010-4 м2Q
- 16. В плоском горизонтально расположенном конденсаторе, расстояние между
- 17. d = 0,01 мm = 510-14 кгU
- 18. Между двумя вертикальными пластинами на одинаковом расстоянии
- 19. yДано:t – ?l – ? Fсопр=mg. (1)
- 20. Между двумя вертикальными пластинами, находящимися на расстоянии
- 21. Дано:Решение:q – ? Найдем проекции векторов на
- 22. Электрон с некоторой начальной скоростью v0 влетает
- 23. Ответ: чтобы электрон и альфа-частица не вылетели
- 24. Протон и альфа-частица с одинаковой скоростью влетают
- 25. Дано: вследствие того что Решение:dly-q+qyU F=eE,ускорение по
- 26. Пучок электронов, ускоренных разностью потенциалов U=300В при
- 27. Дано:Решение:U1 – ? A=qU Найдем v0. Если
- 28. Скачать презентанцию
ПотенциалРазность потенциалов между двумя точками электрического поля определяется работой, которую надо совершить, чтобы единицу заряда перенести из одной точки в другуюПотенциал точечного зарядагде r – расстояние от заряда.Напряженность электрического поля и
Слайды и текст этой презентации
Слайд 2Потенциал
Разность потенциалов между двумя точками электрического поля определяется
работой, которую
надо совершить, чтобы единицу заряда перенести из одной
точки в
другуюПотенциал точечного заряда
где r – расстояние от заряда.
Напряженность электрического поля и потенциал связаны соотношением
где U – разность потенциалов между пластинами конденсатора,
d – расстояние между ними.
1) Шаровой конденсатор
Разность потенциалов между внутренней сферой и какой-либо точкой внутри
конденсатора, удаленной на расстояние r от центра конденсатора, равна
где а – радиус внутренней сферы.
2) Плоский конденсатор
Разность потенциалов между положительно заряженной пластиной и произвольной
точкой, удаленной на расстояние х от нее, равна
Слайд 33) Цилиндрический конденсатор
Разность потенциалов между внутренним цилиндром и произвольной точкой
между
электродами равна
где а – радиус внутреннего цилиндра,
q1 –
заряд внутреннего цилиндра на единицу длины.
Слайд 4Шарик массой m=40 мг, заряженный положительным зарядом q1=1нКл, движется со
скоростью v=10см/с На какое расстояния r может приблизиться шарик к
положительному заряду q2=1,3 нКл?
Условие задачи
Задача №1
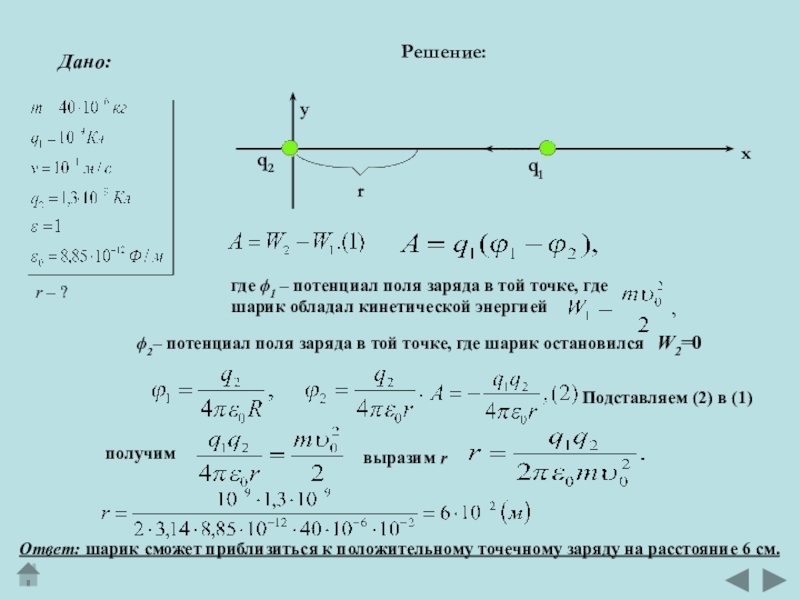
Слайд 5Дано:
r – ?
Решение:
W2=0
выразим r
где 1 – потенциал поля
заряда в той точке, где
шарик обладал кинетической энергией
2–
потенциал поля заряда в той точке, где шарик остановился Подставляем (2) в (1)
получим
Ответ: шарик сможет приблизиться к положительному точечному заряду на расстояние 6 см.
q2
y
x
q1
r
Слайд 6На какое расстояние могут сблизиться два электрона, если они движутся
навстречу
друг другу с относительной скоростью 108 см/с?
Условие задачи
Задача №2
Слайд 7Ответ: два электрона, летящие с относительной скоростью =106 м/с могут
сблизиться до
расстояния
Дано:
r – ?
Решение:
где 1 – потенциал
поля электрона в той точке, где другой электрон обладал кинетической энергией
выразим r
Подставим (2) в (1), получаем
с учетом того, что 2=0:
r
y
x
Слайд 8Два шарика с зарядами q1=6,6нКл и q2=13,3 нКл находятся на
расстоянии r1=40см.
Какую работу нужно совершить, чтобы сблизить их до
расстояния r2=25см?Условие задачи
Задача №3
Слайд 9Дано:
Решение:
А – ?
Получим
Второй способ
Первый способ
потенциальная энергия
заряда
q2 в точках 1 и 2 соответственно.где 2, и 1 – потенциалы электростатического
поля заряда в точках 2 и 1 соответственно
Ответ: чтобы шарики сблизить до расстояния r2=25 см,
надо совершить работу А=
Слайд 10Какая работа А совершается при перенесении точечного заряда q=20нКл из
бесконечности в точку, находящуюся на расстоянии 1см от поверхности шара
радиусом 1см с поверхностной плотностью заряда =10-5 Кл/м2? =10-5 Кл/м2?
Условие задачи
Задача №4
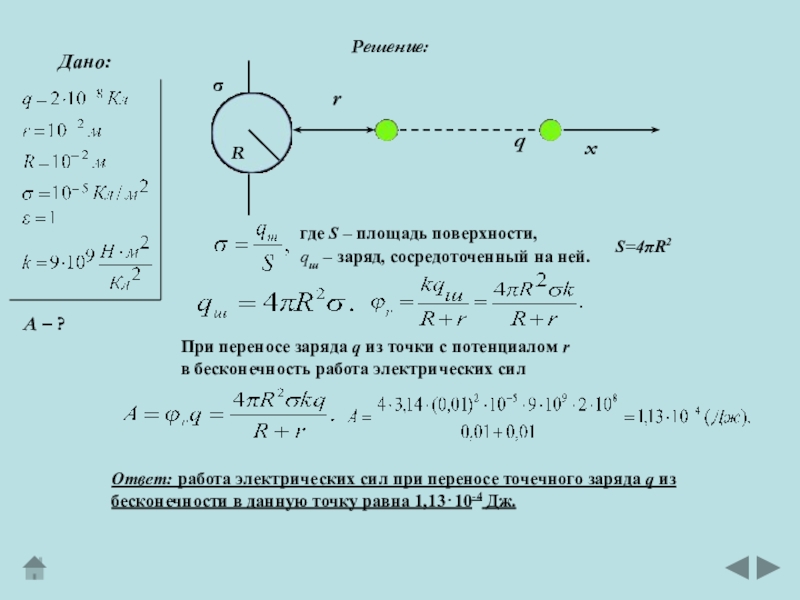
Слайд 11Дано:
Решение:
А – ?
где S – площадь поверхности,
qш –
заряд, сосредоточенный на ней.
S=4R2
При переносе заряда q из
точки с потенциалом r в бесконечность работа электрических сил
Ответ: работа электрических сил при переносе точечного заряда q из
бесконечности в данную точку равна 1,1310-4 Дж.
x
q
r
σ
R
Слайд 12На расстоянии r1=4см от бесконечно длинной заряженной нити находится точечный
заряд q=0,66 нКл. Под действием поля заряд приближается к нити
на расстояние r2=2см, при этом совершается работа А=50эрг. Найти линейную плотность заряда на нити.
Условие задачи
Задача №5
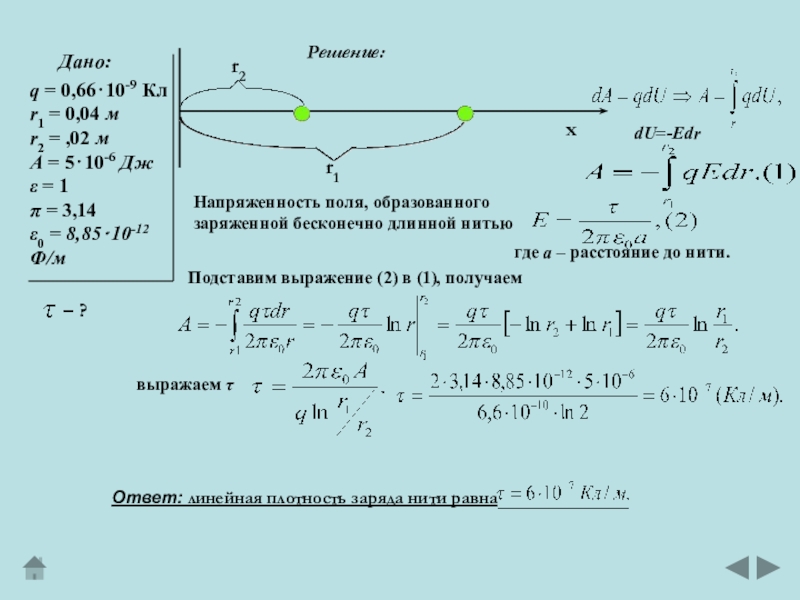
Слайд 13Дано:
Решение:
– ?
q = 0,6610-9 Кл
r1 = 0,04
м
r2 = ,02 м
А = 510-6 Дж
= 1
=
3,140 = 8,8510-12 Ф/м
dU=-Edr
Подставим выражение (2) в (1), получаем
Напряженность поля, образованного
заряженной бесконечно длинной нитью
где а – расстояние до нити.
выражаем
Ответ: линейная плотность заряда нити равна
r2
r1
x
Слайд 14Разность потенциалов между пластинами плоского конденсатора U=90В.
Площадь каждой пластины
S=60см2 и заряд q=1нКл. На каком расстоянии
друг от друга
находятся пластины?Условие задачи
Задача №6
Слайд 15U = 90 В
S = 6010-4 м2
Q = 10-9 Кл
= 1
0 = 8,8510-12 Ф/м
Дано:
Решение:
d – ?
при =const.
(2) Используем то, что напряженность поля, образованного разноименно заряженными
параллельными бесконечными плоскостями (поле плоского конденсатора)
Подставим (3) в (2), получаем
Так как формулы (1) и (4) являются двумя способами выражения одной и
той же величины, то можно приравнять их
Ответ: расстояние между пластинами конденсатора d=4,8 мм.
-q
+q
S
U
Слайд 16В плоском горизонтально расположенном конденсаторе, расстояние между пластинами
которого d=1
см, находится заряженная капелька массой m=510-11 г. При отсутствии
электрического
поля капелька вследствие сопротивления воздуха падает с некоторойпостоянной скоростью. Если к пластинам конденсатора приложить разность
потенциалов U=600 В, то капелька падает вдвое медленнее. Найти заряд капельки.
Условие задачи
Задача №7
Слайд 17d = 0,01 м
m = 510-14 кг
U = 600 В
1
= 22
g = 9,8 м/с
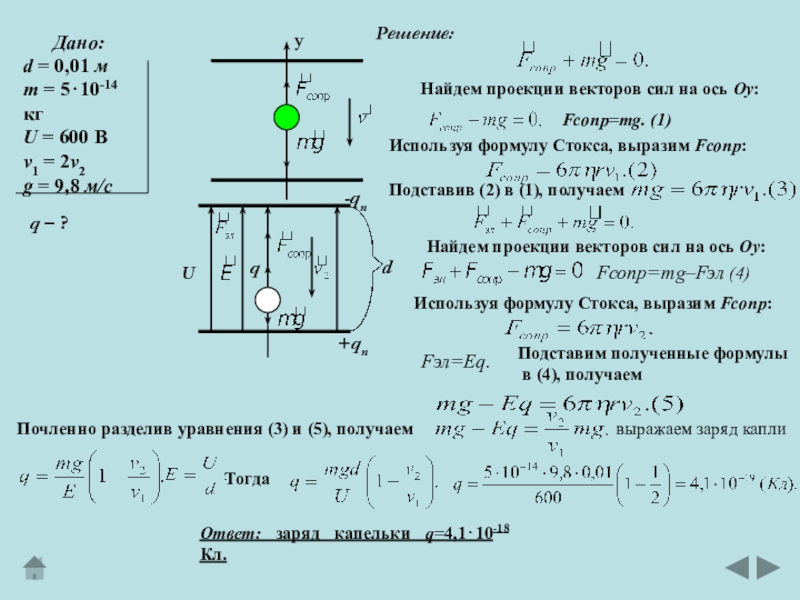
Дано:
Решение:
q – ?
Fсопр=mg. (1)
Fсопр=mg–Fэл (4)
Fэл=Eq.
Найдем проекции векторов сил на ось Оу:
Используя формулу Стокса, выразим Fсопр:
Подставив (2) в (1), получаем
Найдем проекции векторов сил на ось Оу:
Используя формулу Стокса, выразим Fсопр:
Подставим полученные формулы
в (4), получаем
Почленно разделив уравнения (3) и (5), получаем
выражаем заряд капли
Тогда
Ответ: заряд капельки q=4,110-18 Кл.
y
-qn
+qn
d
U
q
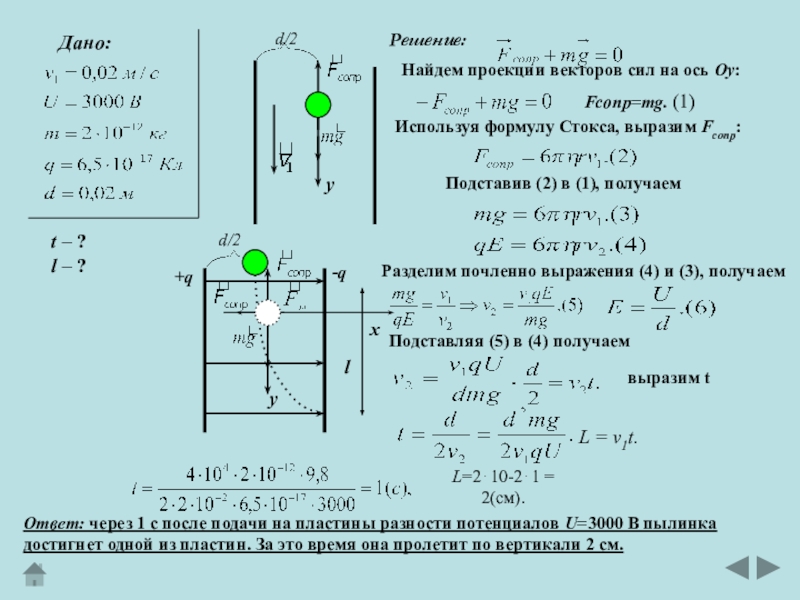
Слайд 18Между двумя вертикальными пластинами на одинаковом расстоянии от них падает
пылинка. Вследствие сопротивления воздуха скорость падения пылинки постоянна
и равна
v=2 см/с. Через какое время после подачи на пластины разности потенциалов U=3 кВ пылинка достигнет одной из пластин? Какое расстояние l по вертикали пылинка
пролетит до попадания на пластину? Расстояние между пластинами d=2 см, масса
пылинки m=210-9 г, ее заряд q=6,510-17 Кл.
Условие задачи
Задача №8
Слайд 19y
Дано:
t – ?
l – ?
Fсопр=mg. (1)
Решение:
Найдем проекции векторов
сил на ось Оу:
Используя формулу Стокса, выразим Fсопр:
Подставив (2) в
(1), получаем Разделим почленно выражения (4) и (3), получаем
Подставляя (5) в (4) получаем
выразим t
L = v1t.
L=210-21 = 2(см).
Ответ: через 1 с после подачи на пластины разности потенциалов U=3000 В пылинка
достигнет одной из пластин. За это время она пролетит по вертикали 2 см.
d/2
d/2
+q
-q
l
x
y
Слайд 20Между двумя вертикальными пластинами, находящимися на расстоянии 1 см друг
от друга, на нити висит заряженный шарик массой 0,1 г.
После того, как на пластины была подана разность потенциалов 1000 В, нить с шариком отклонилась на угол 10.
Найти заряд шарика.
Условие задачи
Задача №9
Слайд 21Дано:
Решение:
q – ?
Найдем проекции векторов на оси Ox и
Оу
Разделим почленно уравнение
(1) на (2), получаем
По определению
И, учитывая
то, что внутри конденсатора имеется однородное электрическое поле с напряженностью
получим из (3)
Ответ: заряд шарика равен
+q
-q
y
a
x
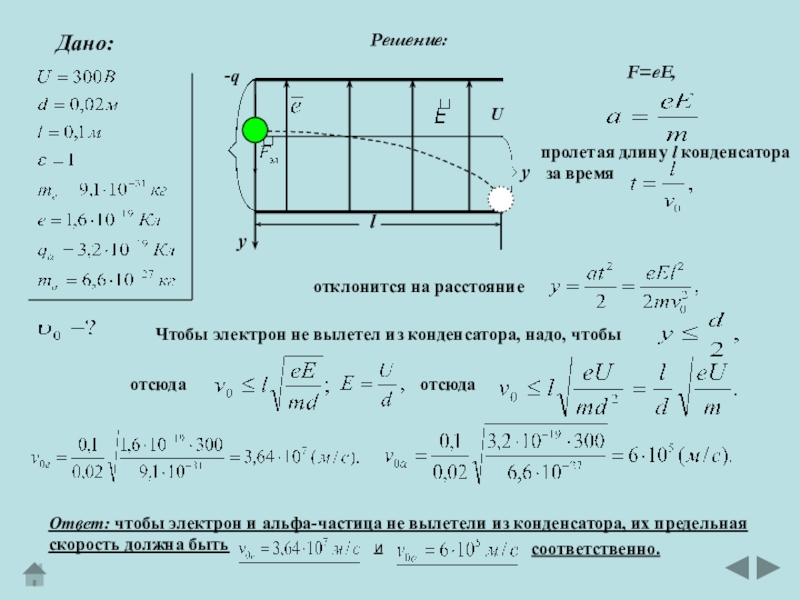
Слайд 22Электрон с некоторой начальной скоростью v0 влетает в плоский, горизонтально
расположенный конденсатор параллельно пластинам на равном расстоянии от них.
К
пластинам конденсатора приложена разность потенциалов U=300 В, расстояние между пластинами d=2 см, длина конденсатора l=10 см. Какова должна быть
предельная начальная скорость электрона v0, чтобы электрон не вылетел из
конденсатора. Решить эту же задачу для альфа-частицы.
Условие задачи
Задача №10
Слайд 23Ответ: чтобы электрон и альфа-частица не вылетели из конденсатора, их
предельная
скорость должна быть
Дано:
Решение:
F=eE,
отклонится на расстояние
Чтобы электрон не
вылетел из конденсатора, надо, чтобыотсюда
отсюда
и
соответственно.
пролетая длину l конденсатора
за время
-q
l
y
y
U
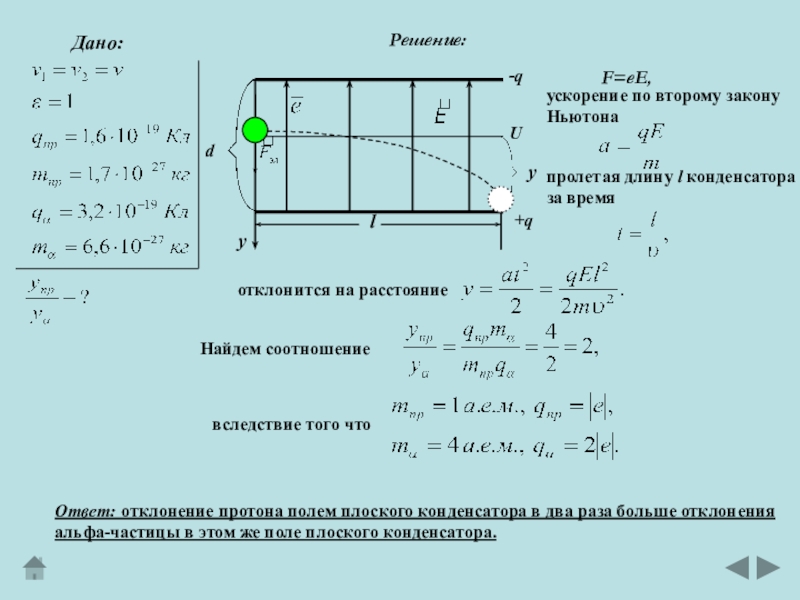
Слайд 24Протон и альфа-частица с одинаковой скоростью влетают в плоский конденсатор
параллельно пластинам. Во сколько раз отклонение протона полем конденсатора
будет
больше отклонения альфа-частицы?Условие задачи
Задача №11
Слайд 25Дано:
вследствие того что
Решение:
d
l
y
-q
+q
y
U
F=eE,
ускорение по второму закону
Ньютона
пролетая
длину l конденсатора
за время
отклонится на расстояние
Найдем соотношение
Ответ: отклонение протона полем плоского конденсатора в два раза больше отклонения
альфа-частицы в этом же поле плоского конденсатора.
Слайд 26Пучок электронов, ускоренных разностью потенциалов U=300В при прохождении через
незаряженный
плоский горизонтально расположенный конденсатор дает светящееся
пятно на флуоресцирующем экране,
расположенном на расстоянии l1=12 см от конца конденсатора. При зарядке конденсатора пятно на экране смещается на
расстояние у=3 см. Расстояние между пластинами конденсатора d=1,4 см, длина
конденсатора l=6 см. Найти разность потенциалов U1, приложенную к пластинам
конденсатора.
Условие задачи
Задача №12
Слайд 27Дано:
Решение:
U1 – ?
A=qU
Найдем v0. Если ускоряющее поле совершает
над частицей массой m и зарядом q работу
где Е –
напряженность поля между пластинами конденсатора, тоПодставим (3) и
(2) в (1), получаем
по оси Ox смещение: x=vxt2,
по оси Оу смещение: y=vy1t2,
Подставим в (5) выражение
(4), (*), (3), (2), получаем
Ответ: разность потенциалов, приложенная к пластинам конденсатора равна U=28 В.
+q
-q
d/2
+q
y1
