Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема №8. Введение в теорию графов
Содержание
- 1. Тема №8. Введение в теорию графов
- 2. 1. Введение2) Термин «граф» впервые ввел в
- 3. 3. Помогают в решении математических и экономических
- 4. Слайд 4
- 5. 1) Граф - совокупность конечного числа точек
- 6. Def.Граф G= - совокупность вершин V и
- 7. 2.Вершины графа, которые не принадлежат ни одному
- 8. 6.Путем от A до X называется последовательность
- 9. 11.Граф называется связным, если каждые две его
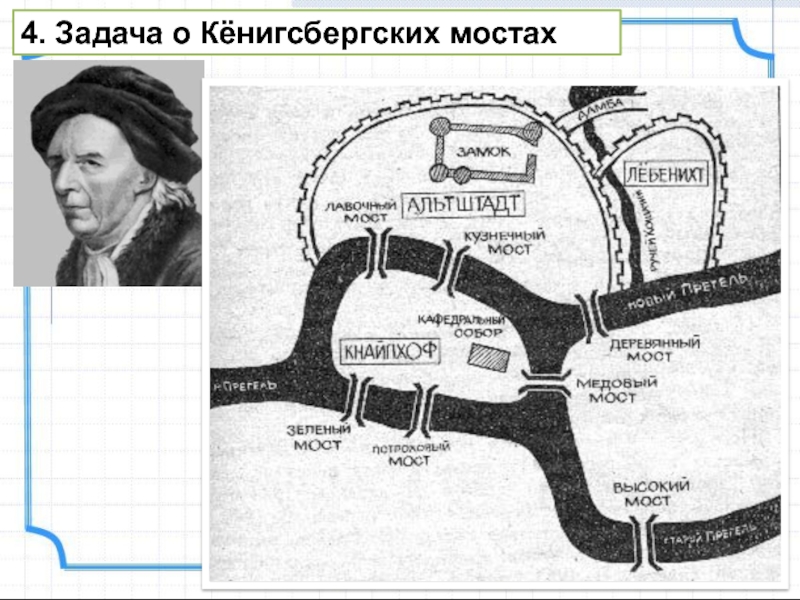
- 10. 4. Задача о Кёнигсбергских мостах
- 11. Кенигсбергские мостыМожно ли обойти все Кенигсбергские мосты, проходя только один раз через каждый из этих мостов?
- 12. Важно, является ли число мостов, ведущих к
- 13. Степень вершиныЗакономерность 1: Если все вершины графа четные, то его можно изобразить «одним росчерком пера».
- 14. Закономерность 2: Граф, имеющий всего две нечетные
- 15. Закономерность 3: Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
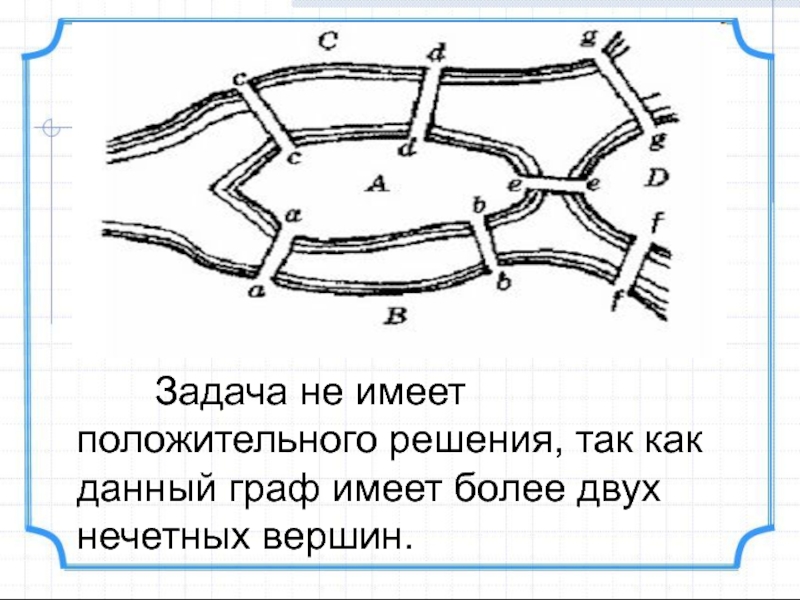
- 16. Какие вершины четные, а какие нечетные? Подпишем степени вершин в кружочках.Нечетные вершины: А, B, C, D.3335
- 17. Задача не имеет
- 18. Граф имеет цикл, содержащий все ребра графа
- 19. Алгоритм решения задач1. Нарисовать граф, где вершины
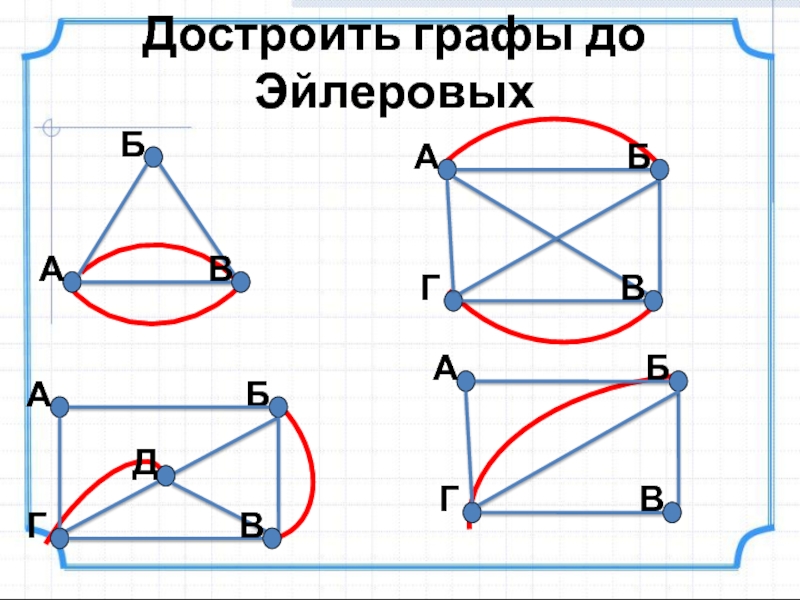
- 20. Достроить графы до Эйлеровых
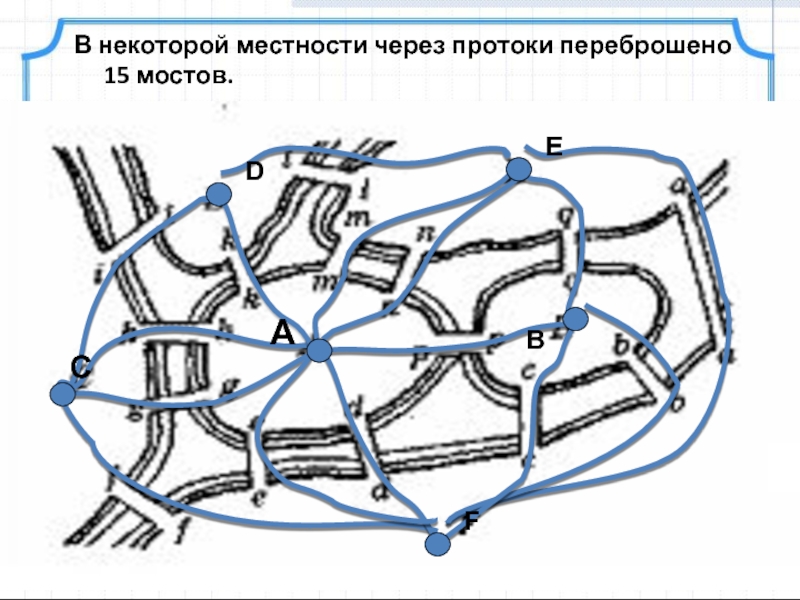
- 21. В некоторой местности через протоки переброшено 15 мостов.
- 22. Построим граф, где вершины – острова и
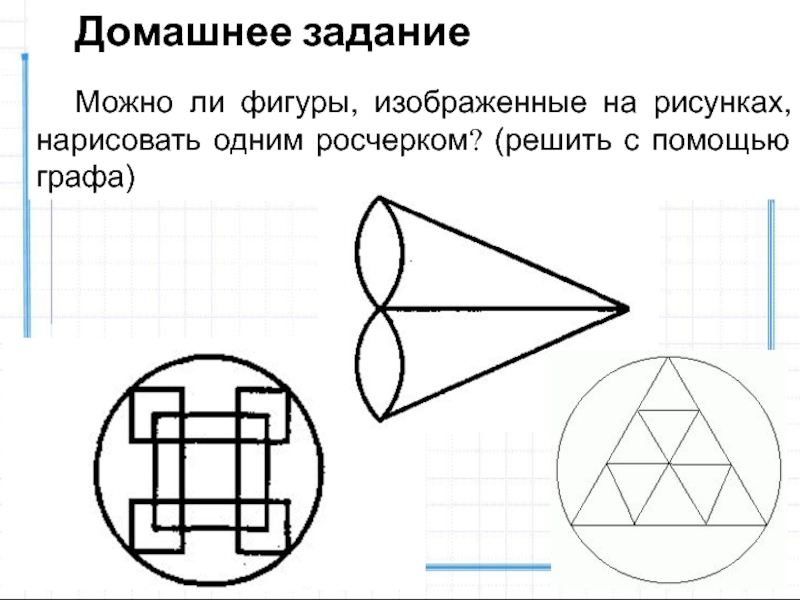
- 23. Домашнее задание Можно ли фигуры, изображенные на рисунках, нарисовать одним росчерком? (решить с помощью графа)
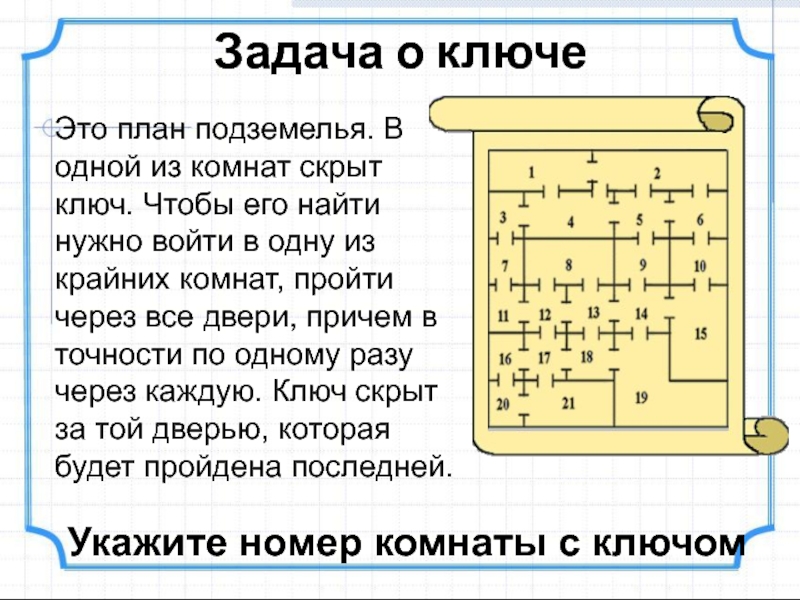
- 24. Задача о ключеЭто план подземелья. В одной
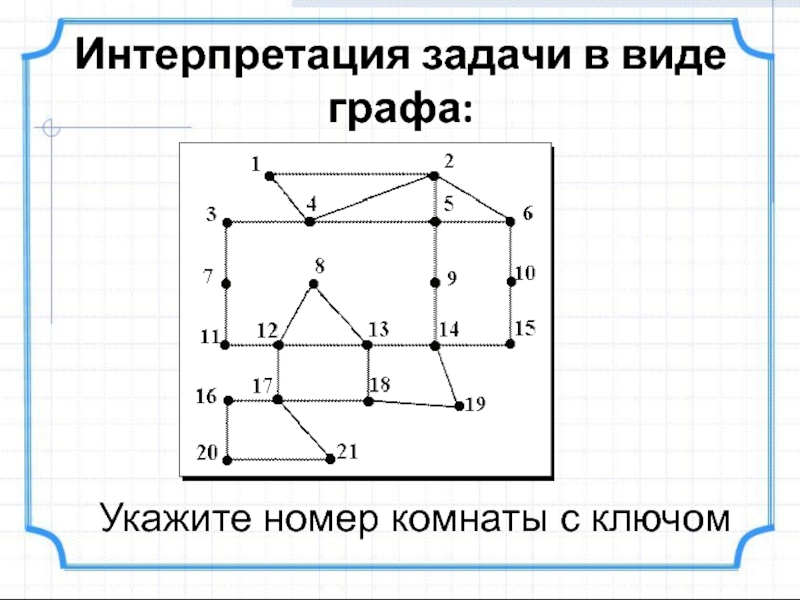
- 25. Интерпретация задачи в виде графа:Укажите номер комнаты с ключом
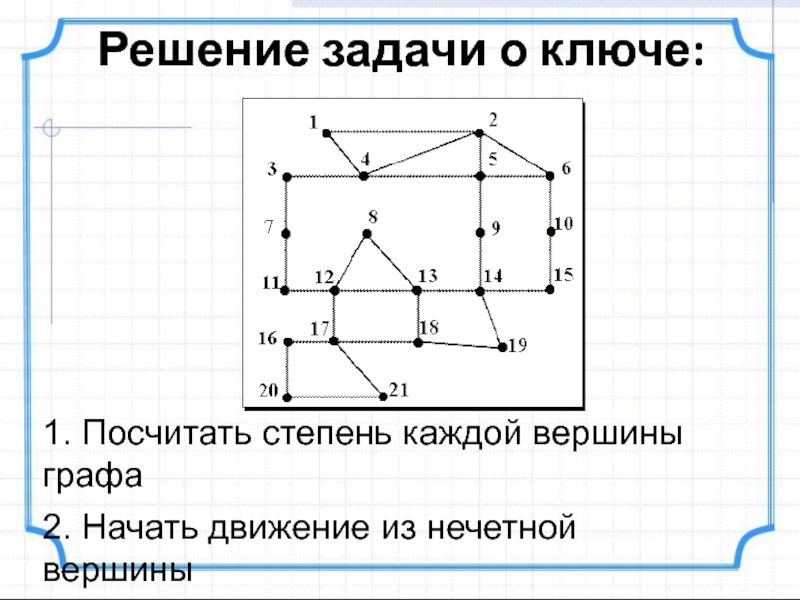
- 26. Решение задачи о ключе:1. Посчитать степень каждой вершины графа2. Начать движение из нечетной вершины
- 27. Домашнее задание
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1МБОУ г. Иркутска лицей ИГУ,
ligu.edu38.ru
Раздел II.
Элементы математической логики
Дискретная математика, 10
класс
Слайд 21. Введение
2) Термин «граф» впервые ввел в 1936 году венгерский
математик Денеш Кёниг («Теория конечных и бесконечных графов»).
1) Основоположник
теории графов - Леонард Эйлер (1736 год, задача о Кёнигсбергских мостах)Денеш Кёниг (1884-1944)
Леонард Эйлер (1707-1783)
Популяризация ТГ - книга французского математика Клода Бержа: «Теория графов и ее применения», 1960 г.
Клод Берж (1926-2002)
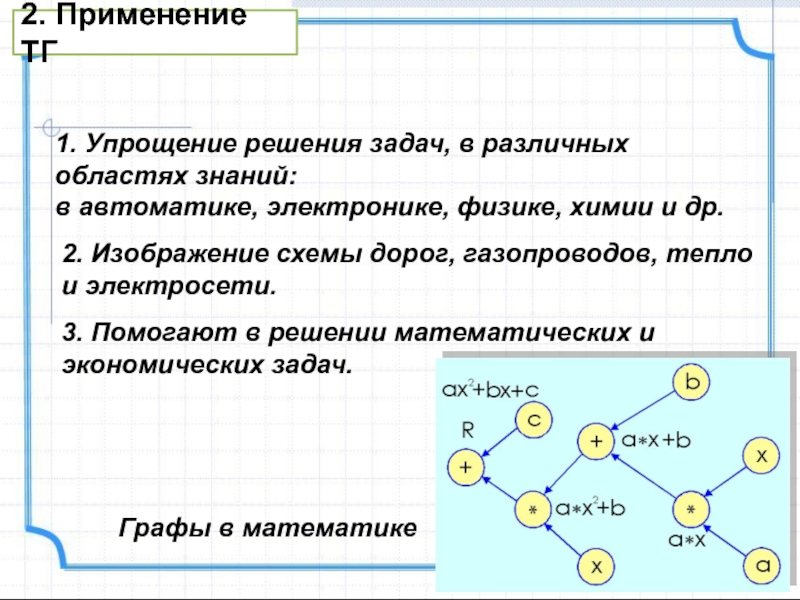
Слайд 33. Помогают в решении математических и экономических задач.
Графы в математике
2.
Применение ТГ
1. Упрощение решения задач, в различных областях знаний:
в
автоматике, электронике, физике, химии и др. 2. Изображение схемы дорог, газопроводов, тепло и электросети.
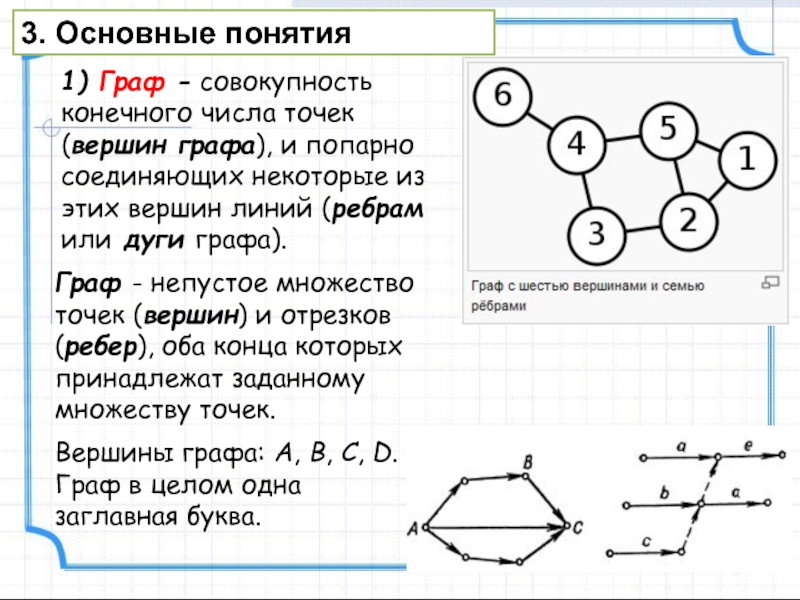
Слайд 51) Граф - совокупность конечного числа точек (вершин графа), и
попарно соединяющих некоторые из этих вершин линий (ребрам или дуги
графа).Вершины графа: A, B, C, D.
Граф в целом одна заглавная буква.
3. Основные понятия
Граф - непустое множество точек (вершин) и отрезков (ребер), оба конца которых принадлежат заданному множеству точек.
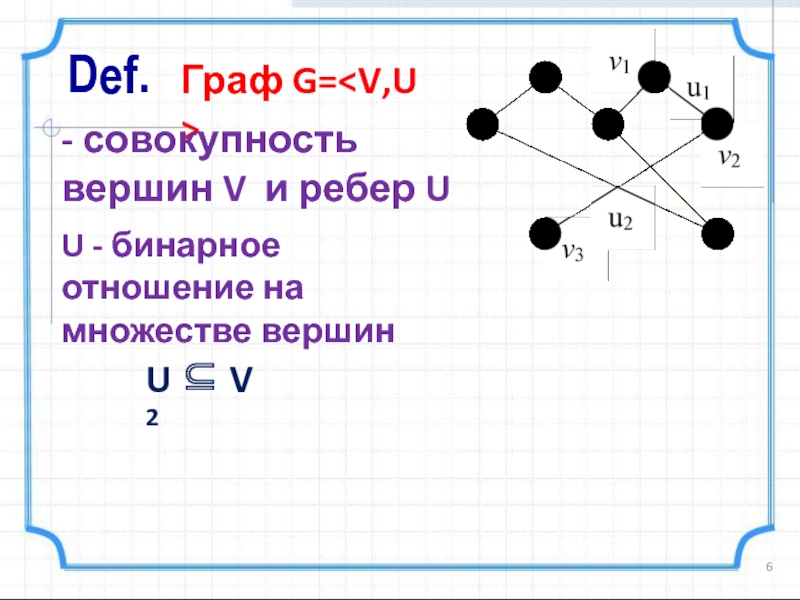
Слайд 6Def.
Граф G=
- совокупность вершин V и ребер U
U - бинарное отношение на множестве вершин
U V 2
Слайд 72.Вершины графа, которые не принадлежат ни одному ребру, называются изолированными.
3.Граф,
состоящий только из изолированных вершин, называется нуль-графом.
Обозначение: O' – граф
с вершинами, не имеющий ребер.4.Граф, в котором каждая пара вершин соединена ребром, называется полным.
Обозначение: U' – граф, состоящий из n вершин и ребер, соединяющих всевозможные пары этих вершин. Такой граф можно представить как n–угольник, в котором проведены все диагонали.
5.Степенью вершины называется число ребер, которым принадлежит вершина.
Обозначение: p (A) – степень вершины A.
Слайд 86.Путем от A до X называется последовательность ребер, ведущая от
A к X, такая, что каждые два соседних ребра имеют
общую вершину, и никакое ребро не встречается более одного раза.7.Циклом называется путь, в котором совпадают начальная и конечная точка.
8.Простым циклом называется цикл, не проходящий ни через одну из вершин графа более одного раза.
9. Длиной пути, проложенного на цикле, называется число ребер этого пути.
Слайд 911.Граф называется связным, если каждые две его вершины связны; если
же в графе найдется хотя бы одна пара несвязных вершин,
то граф называется несвязным.12.Деревом называется связный граф, не содержащий циклов.
13.Несвязный граф, состоящий исключительно из деревьев, называется лесом.
10.Две вершины A и B в графе называются связными (несвязными), если в нем существует (не существует) путь, ведущий из A в B.
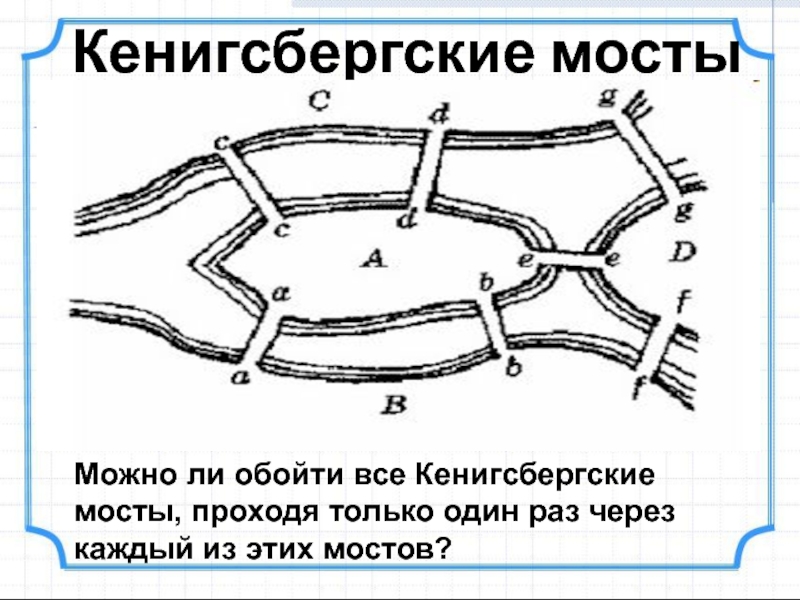
Слайд 11Кенигсбергские мосты
Можно ли обойти все Кенигсбергские мосты, проходя только один
раз через каждый из этих мостов?
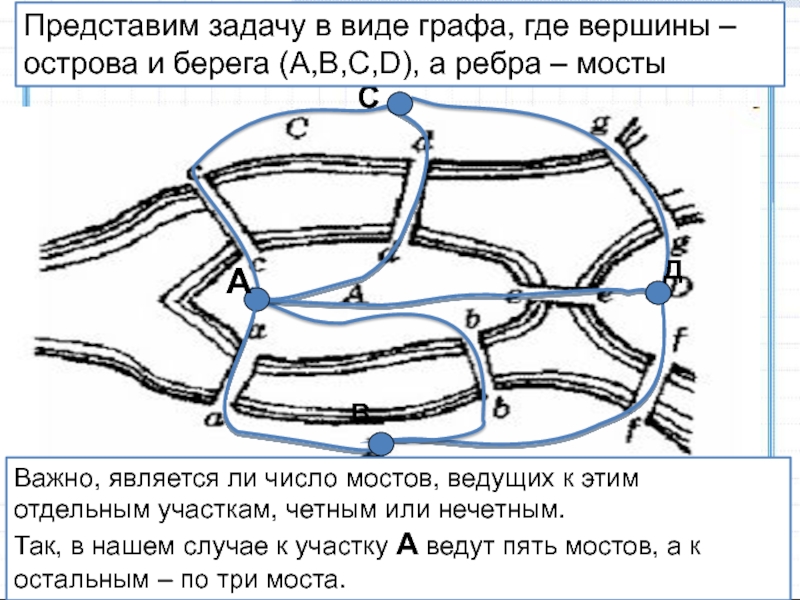
Слайд 12Важно, является ли число мостов, ведущих к этим отдельным участкам,
четным или нечетным.
Так, в нашем случае к участку A
ведут пять мостов, а к остальным – по три моста.Представим задачу в виде графа, где вершины – острова и берега (A,B,C,D), а ребра – мосты
Слайд 13Степень вершины
Закономерность 1: Если все вершины графа четные, то его
можно изобразить «одним росчерком пера».
Слайд 14Закономерность 2: Граф, имеющий всего две нечетные вершины, можно начертить,
не отрывая карандаш от бумаги, при этом движение нужно начать
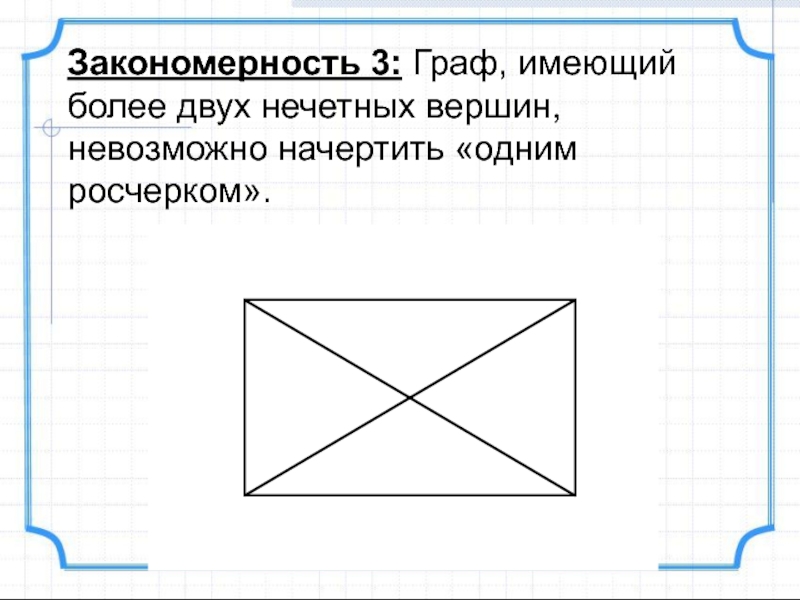
с одной из этих нечетных вершин и закончить во второй из них.Слайд 15Закономерность 3: Граф, имеющий более двух нечетных вершин, невозможно начертить
«одним росчерком».
Слайд 16Какие вершины четные, а какие нечетные? Подпишем степени вершин в
кружочках.
Нечетные вершины: А, B, C, D.
3
3
3
5
Слайд 17 Задача не имеет положительного решения, так
как данный граф имеет более двух нечетных вершин.
Слайд 18Граф имеет цикл, содержащий все ребра графа по одному разу
(Эйлерова линия)
Условия существования Эйлеровой линии:
-граф связный
-все вершины четные
Другими словами,
эйлеров граф – это граф, который можно нарисовать одним росчеркомЭйлеров граф
Слайд 19Алгоритм решения задач
1. Нарисовать граф, где вершины – острова и
берега, а ребра – мосты.
2. Определить степень каждой вершины
и подписать возле нее.3. Посчитать количество нечетных вершин.
4. Обход возможен:
a. ЕСЛИ все вершины – четные, и его можно начать с любого участка.
b. ЕСЛИ 2 вершины – нечетные, но его нужно начать с одной из нечетных местностей.
5. Обход невозможен, если нечетных вершин больше 2.
6. Сделать ВЫВОД.
7. Указать Начало и Конец пути.
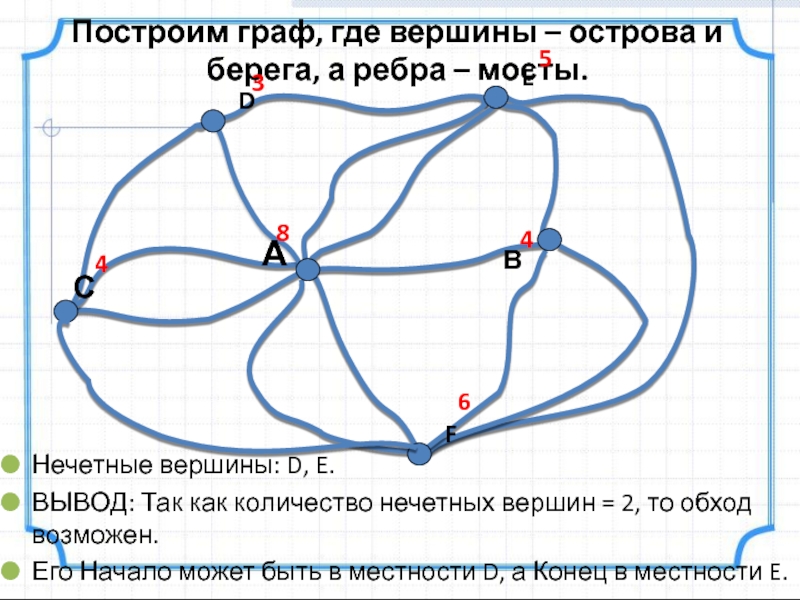
Слайд 22Построим граф, где вершины – острова и берега, а ребра
– мосты.
Нечетные вершины: D, E.
ВЫВОД: Так как количество нечетных вершин
= 2, то обход возможен.Его Начало может быть в местности D, а Конец в местности E.
4
4
6
3
5
8
Слайд 23Домашнее задание
Можно ли фигуры, изображенные на рисунках, нарисовать одним росчерком?
(решить с помощью графа)
Слайд 24Задача о ключе
Это план подземелья. В одной из комнат скрыт
ключ. Чтобы его найти нужно войти в одну из крайних
комнат, пройти через все двери, причем в точности по одному разу через каждую. Ключ скрыт за той дверью, которая будет пройдена последней.Укажите номер комнаты с ключом