ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС

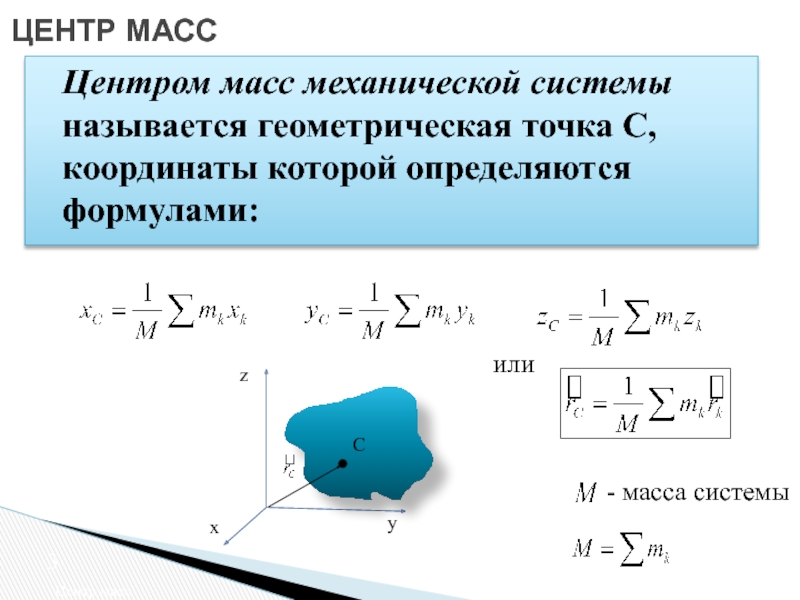
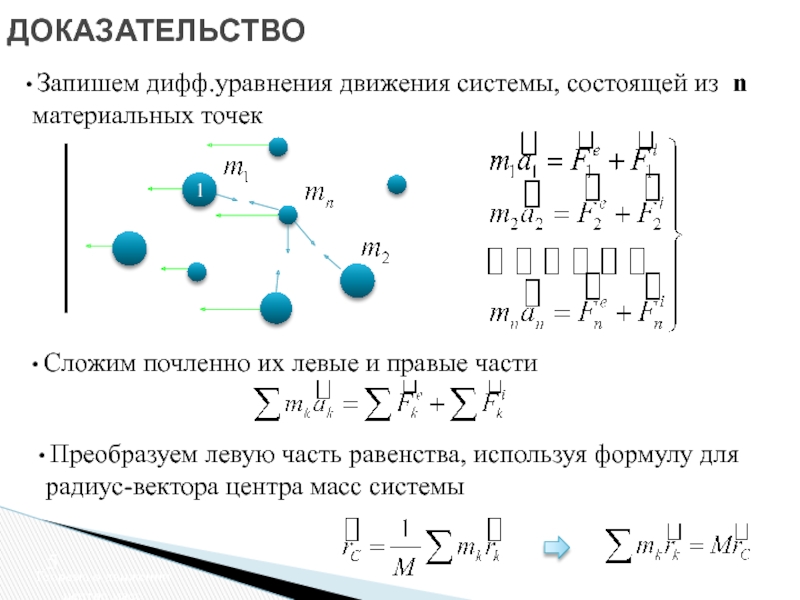
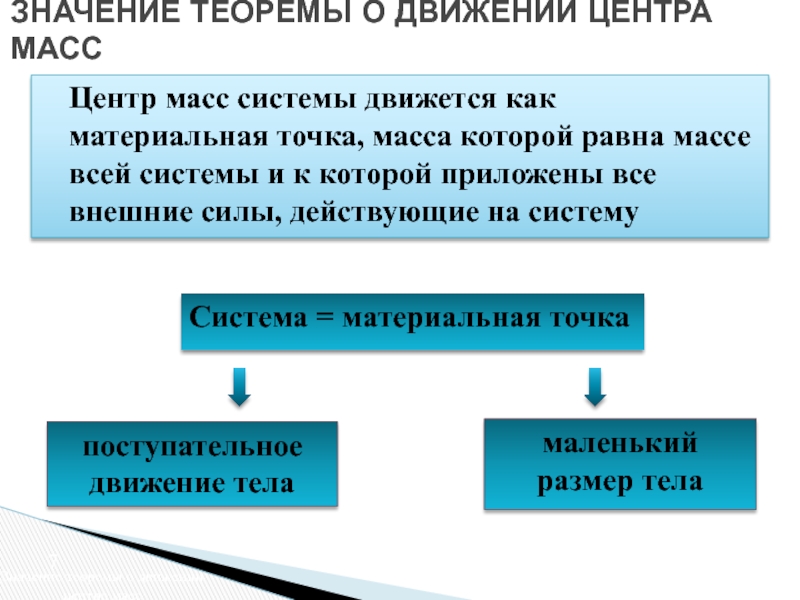
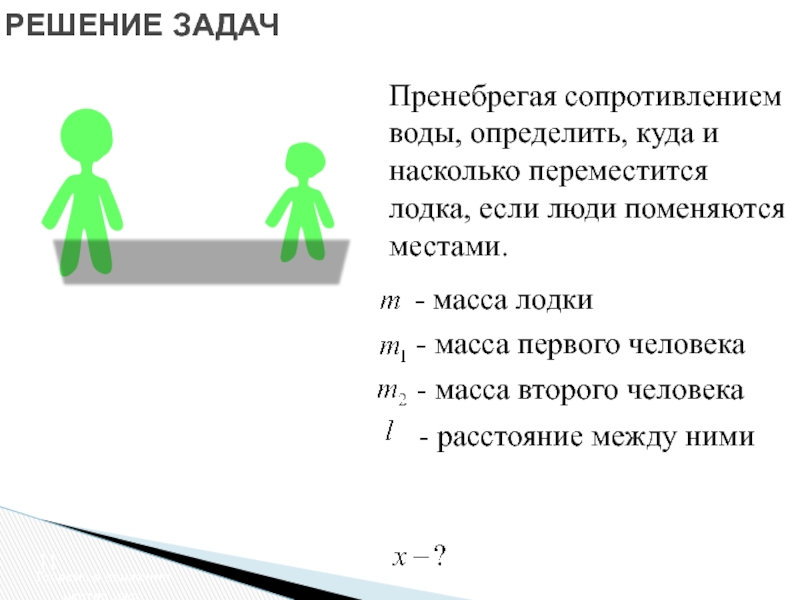
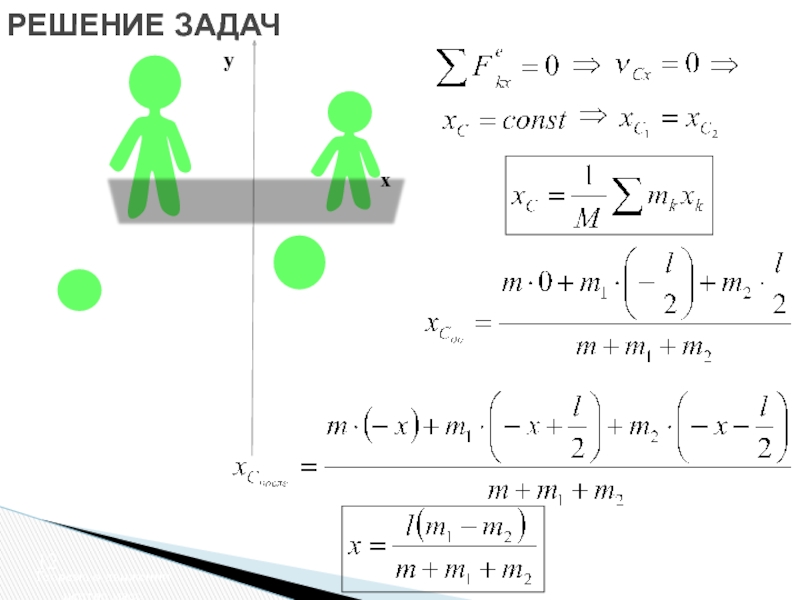
о движении центра масс
Следствия из теоремы
Закон сохранения движения центра масс

Цель

Ознакомиться с теоремой о движении центра масс и примерами ее практического применения.

координаты которой определяются формулами:
или
- масса системы
С
z
x
y

системы на ускорение ее центра масс равно геометрической сумме всех

из n материальных точек
Сложим почленно их левые и правые

Преобразуем левую часть равенства, используя формулу для радиус-вектора центра масс системы

системы
Получим уравнение, выражающее теорему о движении масс системы
Проектируя обе

Теорема доказана

Возьмем вторую производную по времени от обеих частей этого равенства

или

- ускорение масс системы

масс
Центр масс системы движется как материальная точка, масса которой равна

Система = материальная точка

поступательное движение тела

маленький
размер тела

из теоремы
Пара сил, приложенная к твердому телу, не может изменить

СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ

сумма всех внешних сил, действующих на систему, равна нулю, то

или

сумма проекций всех действующих внешних сил на какую-нибудь ось равна

или

и насколько переместится лодка, если люди поменяются местами.
- расстояние между

- масса лодки

- масса второго человека

- масса первого человека

- расстояние от человека до центра лодки