Теоретическая механика

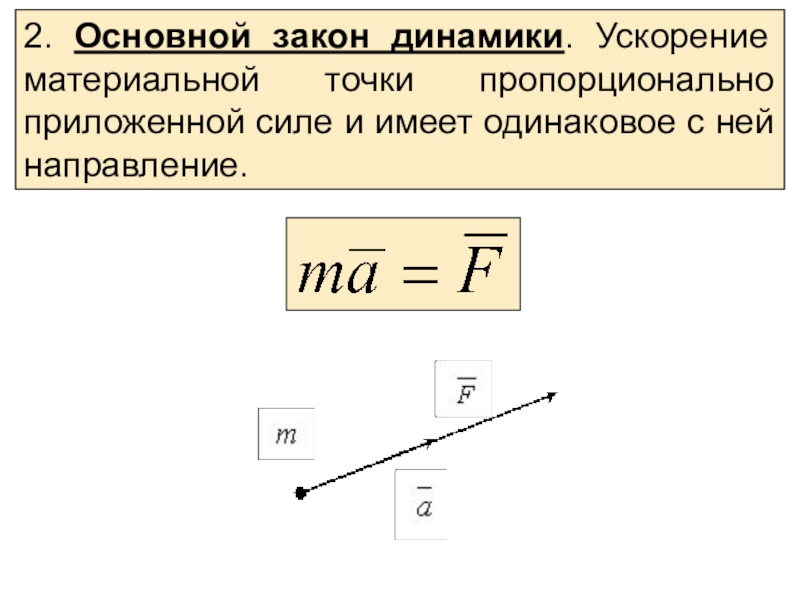
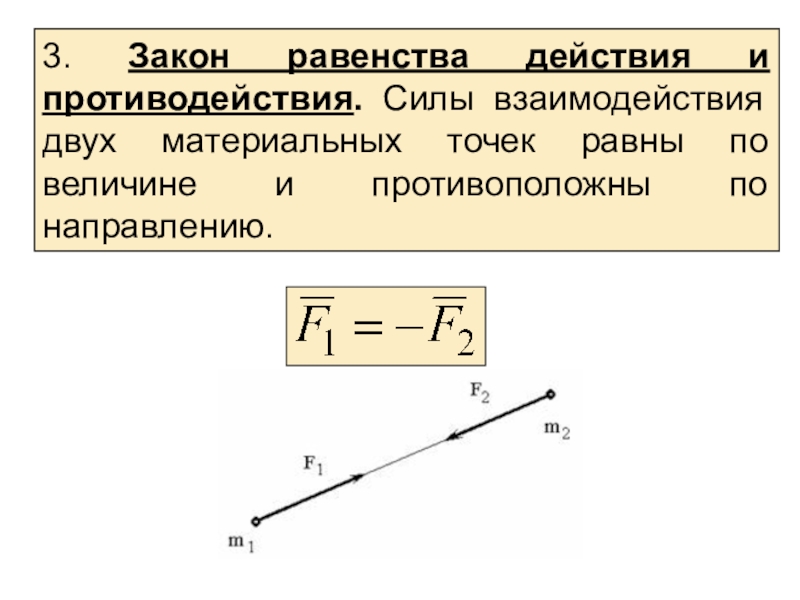
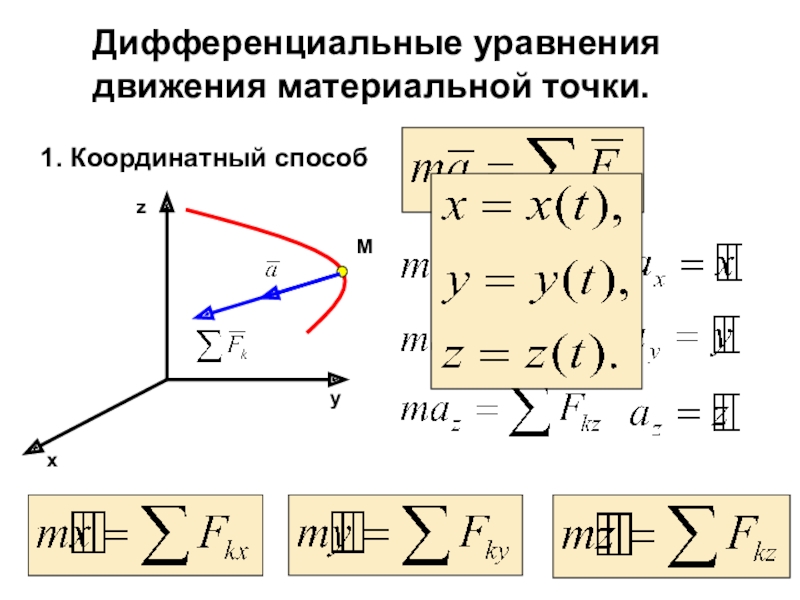
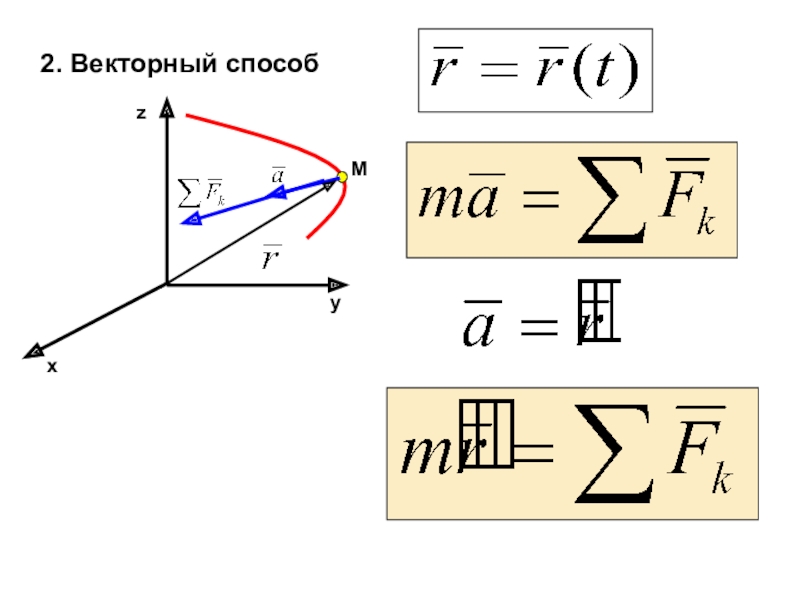
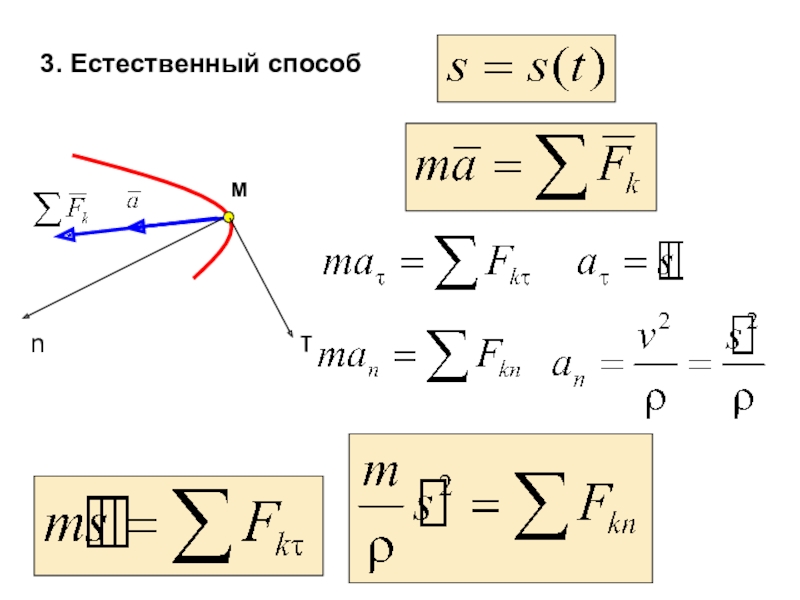
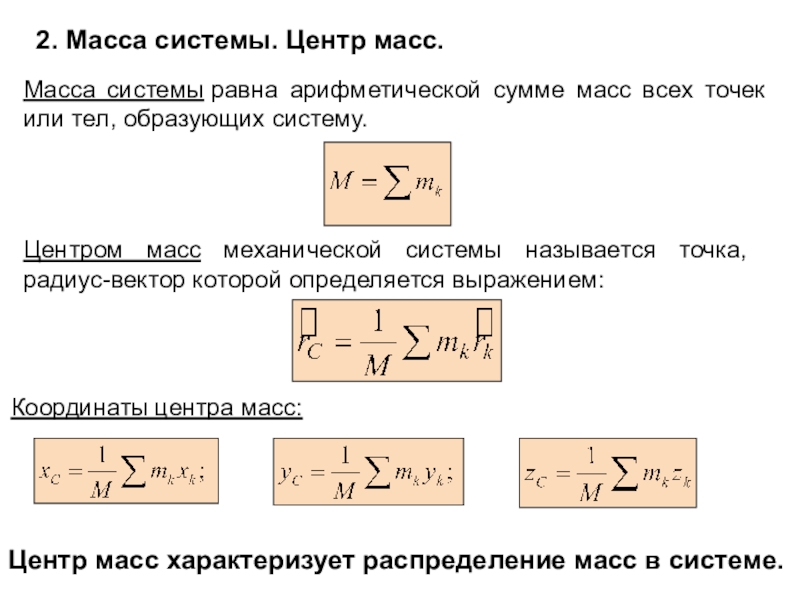
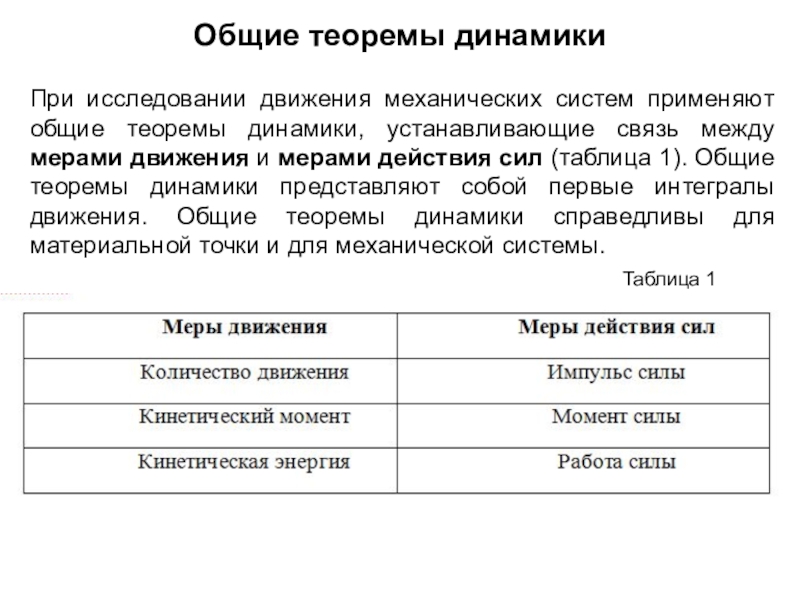
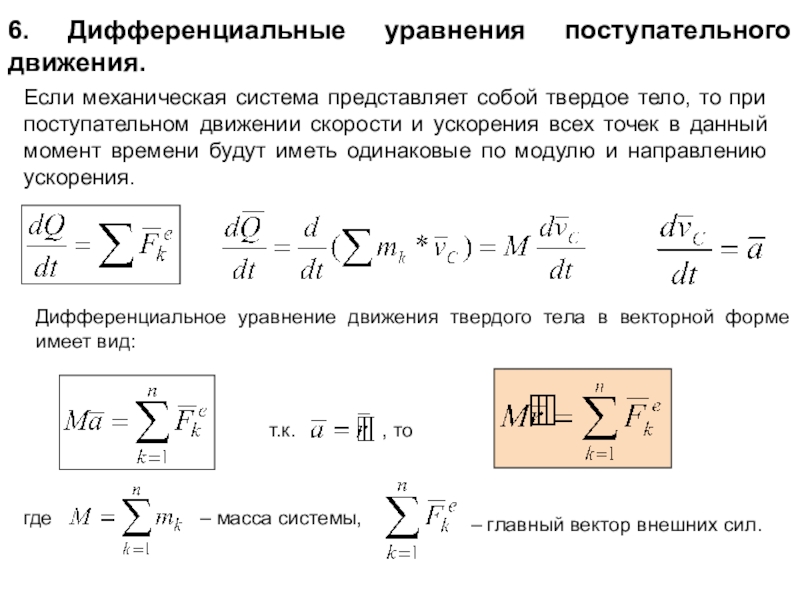
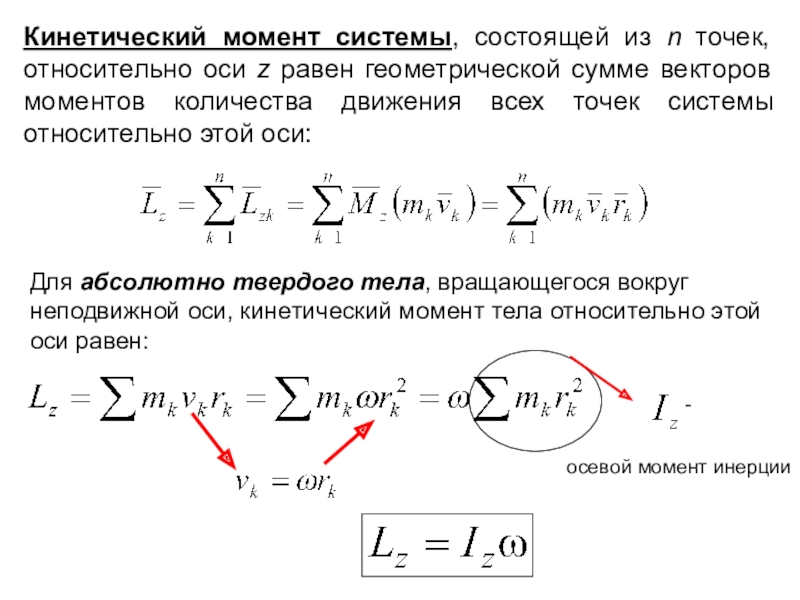
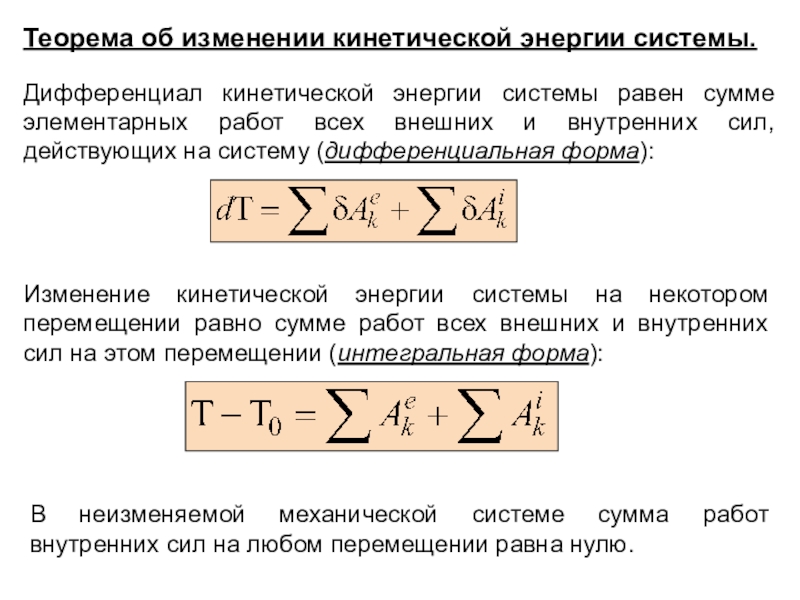
материальных тел под действием сил.
Сила – векторная мера взаимодействия тел.

В динамике силы – переменные.

Силы могут зависеть от:
времени
положения тела
скорости

скорость своего движения под действием приложенных сил.
Масса – мера

покоя или равномерного прямолинейного движения, пока действие других тел не

Точка, на которую не действуют никакие силы со стороны других тел, называется изолированной.

Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета.

и имеет одинаковое с ней направление.

точек равны по величине и противоположны по направлению.

точку сил сообщают точке такое ускорение, какое сообщила бы их

заданному закону движения определить силы, действующие на точку.
Первая задача

на точку, определить закон ее движения.
В обратной задаче динамики решение

Первый интеграл дает закон изменения скорости.
Второй интеграл – закон движения.

При решении второй задачи динамики надо задавать так называемые начальные условия

твердых тел или абсолютно твердых тел и материальных точек, движения

Классификация сил, действующих на мех-ую систему:

силы активные и реакции связей;

силы внешние и внутренние.

входящих в эту систему.
Внутренние силы
силы взаимодействия между точками одной

сил в системе равен нулю. Т.к. внутренние силы – это

2) Главный момент внутренних сил равен нулю относительно любого центра и любой оси

перемещении.
Неизменяемая механическая система – это механическая система, в которой расстояние

точек или тел, образующих систему.
Центром масс механической системы называется точка,

Координаты центра масс:

Центр масс характеризует распределение масс в системе.

относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная

Радиусом инерции тела относительно оси Оz называется линейная величина i определяемая равенством  

Радиус инерции геометрически равен расстоянию от оси Оz до той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.

Следовательно, для всей системы будет:
Для решения многих задач динамики вместо

связь между мерами движения и мерами действия сил (таблица 1).

Таблица 1

Общие теоремы динамики

точки – вектор, численно равный произведению массы точки на ее

Количество движения является мерой механического движения.
Вектор количества движения имеет направление скорости и приложен к точке.

Количество движения механической системы – вектор, численно равный главному вектору количеств движения всех точек системы

времени.
Элементарный импульс силы:
Направлен элементарный импульс по линии действия силы.
Полный

.

Импульс силы за любой промежуток времени τ равен определенному интегралу от элементарного импульса, взятому в пределах от 0 до τ.

движения механической системы по времени равна главному вектору всех внешних

Главный вектор внутренних сил равен нулю по свойству внутренних сил.

2. Интегральная форма. Изменение количества движения системы за некоторый промежуток времени равно векторной сумме всех импульсов внешних сил, действующих на систему

Векторная сумма всех импульсов внутренних сил равна нулю, так как главный вектор внутренних сил равен нулю по свойству внутренних сил.

изменении количества движения.
1. Если главный вектор внешних сил равен нулю,

2. Если проекция главного вектора внешних сил на какую-либо ось (например, на ось x) равна нулю, то проекция вектора количества движения системы на эту же ось постоянна:

Внутренние силы изменить суммарное количество движения системы не могут.

а при сложном движении – как характеристику поступательной части движения

тело, то при поступательном движении скорости и ускорения всех точек

Дифференциальное уравнение движения твердого тела в векторной форме имеет вид:

т.к.

, то

где

– масса системы,

– главный вектор внешних сил.

движения материальной точки массой m, движущейся со скоростью v, относительно

Модуль вектора

:

где h – плечо

Момент количества движения материальной точки относительно оси является скалярной величиной.

равен геометрической сумме векторов моментов количества движения всех точек системы

Для абсолютно твердого тела, вращающегося вокруг неподвижной оси, кинетический момент тела относительно этой оси равен:

-

осевой момент инерции

момента механической системы относительно некоторого центра (оси) равна главному моменту

изменении кинетического момента:
1. Если главный момент всех внешних сил системы

2. Если главный момент всех внешних сил системы относительно некоторой оси равен нулю, то кинетический момент системы относительно этой оси постоянен:

из теоремы об изменении кинетического момента:
, где
Тогда это

При вращательном движении осевой момент инерции является мерой инертности (при поступательном движении мерой инертности является масса).

произведения массы точки на квадрат ее скорости:
Кинетическая энергия механической системы

9. Теорема об изменении кинетической энергии механической системы

–
3) Плоское движение –
Кинетическая энергия тела равна нулю,

ее положения (материальной точки или точки твердого тела).
Работа постоянной

А>0, если

(острый угол)

А=0, если

(прямой угол)

А<0, если

(тупой угол)

Работа отрицательна, когда сила замедляет движение

–
где H – величина вертикального перемещения.
Работа силы тяжести

Работа силы упругости –

– начальная деформация пружины,

– конечная деформация пружины.

Работа силы упругости отрицательна в том случае, когда деформация увеличивается, т.е. когда сила упругости направлена противоположно перемещению ее точки приложения, и положительна, когда деформация уменьшается.

с моментом
–
Работа пары сил с моментом, зависящим от

равен сумме элементарных работ всех внешних и внутренних сил, действующих

Изменение кинетической энергии системы на некотором перемещении равно сумме работ всех внешних и внутренних сил на этом перемещении (интегральная форма):

В неизменяемой механической системе сумма работ внутренних сил на любом перемещении равна нулю.