Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория нормализации
Содержание
- 1. Теория нормализации
- 2. Monday, August 12, 2019СОДЕРЖАНИЕВ чем суть теории
- 3. Monday, August 12, 2019В чем суть теории
- 4. Monday, August 12, 2019Плохие проекты БД (1)Сведения
- 5. Monday, August 12, 2019Плохие проекты БД (2)Аномалии
- 6. Monday, August 12, 2019НормализацияНормализация – это пошаговый
- 7. Monday, August 12, 2019Сложные домены и
- 8. Monday, August 12, 2019Функциональная зависимостьПусть задано отношение
- 9. Monday, August 12, 2019КлючиНабор К атрибутов отношения
- 10. Monday, August 12, 2019Свойства функциональных зависимостейСвойства 1), 2), 3) составляют систему аксиом Армстронга
- 11. Monday, August 12, 2019Логические следствия зависимостейПусть в
- 12. Monday, August 12, 2019Замыкание, полнота, эквивалентность и
- 13. Monday, August 12, 2019FD и сущности предметной
- 14. Monday, August 12, 2019Неполная (частичная) функциональная
- 15. Monday, August 12, 2019Аномалии вставки, удаления, замены
- 16. Monday, August 12, 2019Вторая нормальная форма (2NF)
- 17. Monday, August 12, 2019Пример приведения в 2NFПОКУПАТЕЛИ-ПОКУПКИПОКУПАТЕЛИПОКУПКИ
- 18. Monday, August 12, 2019Пример приведения в 2NF
- 19. Monday, August 12, 2019Транзитивная зависимость и 3NF1)
- 20. Monday, August 12, 2019Аномалии вставки, удаления, замены
- 21. Monday, August 12, 2019Третья нормальная форма (3NF)Отношение
- 22. Monday, August 12, 2019Пример приведения в 3NF КАФЕДРЫФАКУЛЬТЕТЫ
- 23. Monday, August 12, 2019Пример приведения в 3NF
- 24. Monday, August 12, 2019Усиленная 3NF (S3NF) 3NF
- 25. Monday, August 12, 2019Приведение в S3NF Алгоритм
- 26. Monday, August 12, 2019Нормальная форма Бойса-Кодда (BCNF)Отношение
- 27. Monday, August 12, 2019Многозначная зависимость и 4NF
- 28. Monday, August 12, 2019Определение многозначной зависимости
- 29. Monday, August 12, 2019Аксиомы MVDПусть R состоит
- 30. Monday, August 12, 2019Аксиомы связи FD и
- 31. Monday, August 12, 2019Дополнительные свойства MVD1) ОбъединениеЕсли
- 32. Monday, August 12, 2019Четвертая нормальная форма (4NF)Отношение
- 33. Monday, August 12, 2019Приведение в 4NF и
- 34. Monday, August 12, 2019Зависимость по соединению (JD)
- 35. Monday, August 12, 2019Связь зависимостей по соединению
- 36. Monday, August 12, 2019Пятая нормальная форма -
- 37. Monday, August 12, 2019Пример отношения в 5NFПусть
- 38. Monday, August 12, 2019Пример отношения, нарушающего 5NF,
- 39. Monday, August 12, 2019Пример отношения, нарушающего 4NF,
- 40. Monday, August 12, 2019Проектирование схемы реляционной
- 41. Monday, August 12, 2019Формальная постановка задачи
- 42. Monday, August 12, 2019Декомпозиция схемы реляционного
- 43. Monday, August 12, 2019Эквивалентность схем отношений
- 44. Monday, August 12, 2019Эквивалентность отношений по даннымЭквивалентность
- 45. Monday, August 12, 2019Эквивалентность нормальных формСвойство соединения
- 46. Monday, August 12, 2019Критерий качества реляционной схемыРассмотрим
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 8. Теория нормализации отношений реляционной модели
Национальный авиационный университет
Факультет компьютерных
наук
Слайд 2Monday, August 12, 2019
СОДЕРЖАНИЕ
В чем суть теории нормализации РМ
Плохие проекты
БД
Функциональные зависимости
Многозначные зависимости
Зависимости по соединению
Нормальные формы
Проектирование схемы реляционной модели данных
Слайд 3Monday, August 12, 2019
В чем суть теории нормализации
Теория нормализации схем
отношений реляционной модели
данных – это теория, устанавливающая:
каким образом
исходная схема отношений может быть
преобразована в другую результирующую схему, которая эквивалентна в некотором смысле исходной и
в каком-то смысле лучше ее.
Таким образом эта теория должна ответить на следующие вопросы:
какие существуют критерии эквивалентности схем отношений;
какие существуют критерии оценки качества схем отношений;
какие существуют механизмы эквивалентных преобразо- ваний схем отношений, дающие более качественные схемы.
Слайд 4Monday, August 12, 2019
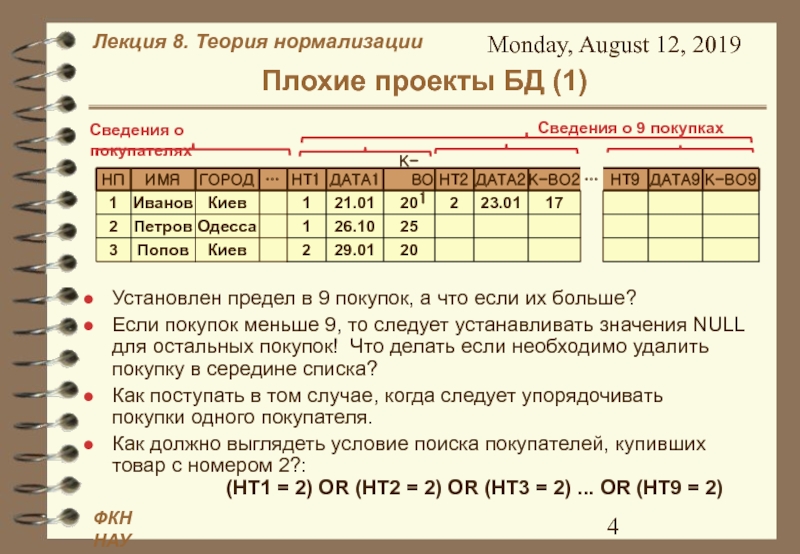
Плохие проекты БД (1)
Сведения о покупателях
Установлен предел
в 9 покупок, а что если их больше?
Если покупок
меньше 9, то следует устанавливать значения NULL
для остальных покупок! Что делать если необходимо удалить
покупку в середине списка? Как поступать в том случае, когда следует упорядочивать покупки одного покупателя.
Как должно выглядеть условие поиска покупателей, купивших товар с номером 2?: (НТ1 = 2) OR (НТ2 = 2) OR (НТ3 = 2) ... OR (НТ9 = 2)
Сведения о 9 покупках
Слайд 5Monday, August 12, 2019
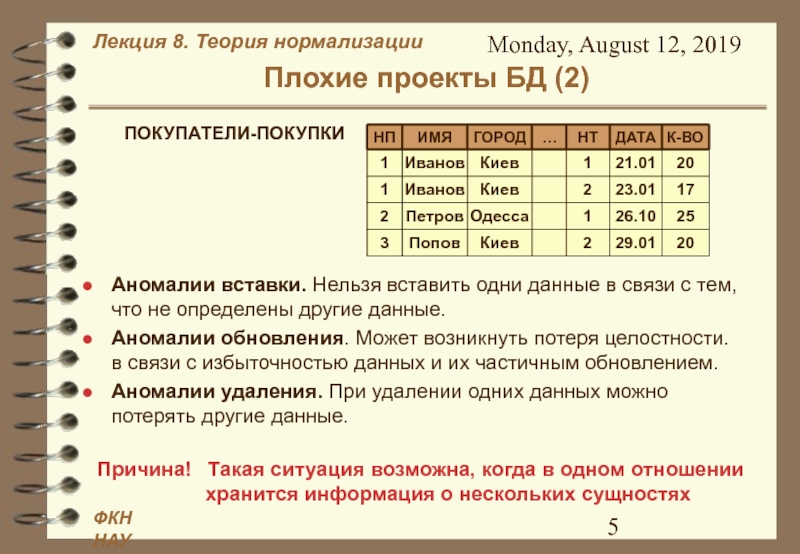
Плохие проекты БД (2)
Аномалии вставки. Нельзя вставить
одни данные в связи с тем, что не определены другие
данные.Аномалии обновления. Может возникнуть потеря целостности. в связи с избыточностью данных и их частичным обновлением.
Аномалии удаления. При удалении одних данных можно потерять другие данные.
Причина! Такая ситуация возможна, когда в одном отношении хранится информация о нескольких сущностях
ПОКУПАТЕЛИ-ПОКУПКИ
Слайд 6Monday, August 12, 2019
Нормализация
Нормализация – это пошаговый обратимый процесс эквивалентного
преобразования одной схемы отношений в другую, которая обладает улучшенными характеристиками
по сравнению с предыдущей. Каждый из таких этапов преобразования называется нормальной формой.Составные (неатомарные) данные - 1NF
Неполная (частичная) функциональная зависимость - 2NF
Транзитивная функциональная зависимость - 3NF
Многозначная зависимость - 4NF
Зависимость по соединению - 5NF
Виды нежелательных свойств отношений и нормальные формы,
которые их устраняют:
Слайд 7Monday, August 12, 2019
Сложные домены и
первая нормальная форма (1NF)
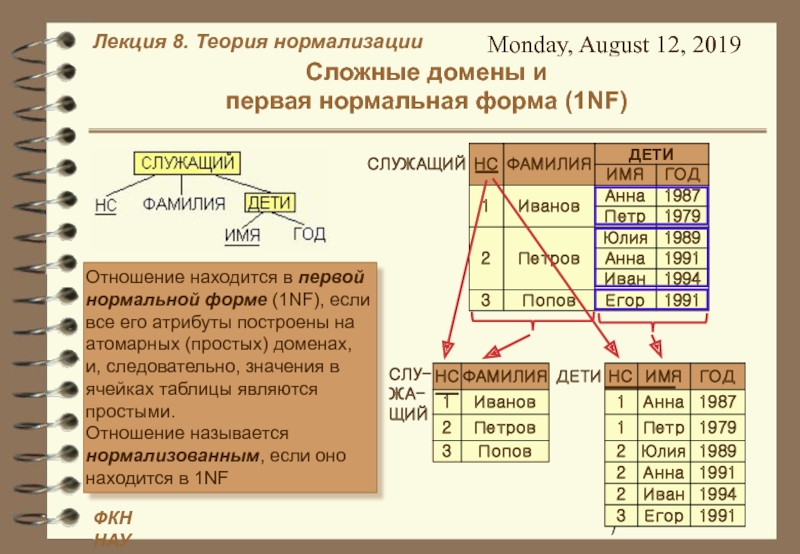
Отношение находится в первой нормальной форме (1NF), если все его
атрибуты построены на атомарных (простых) доменах, и, следовательно, значения в ячейках таблицы являются простыми. Отношение называется нормализованным, если оно находится в 1NF
Слайд 8Monday, August 12, 2019
Функциональная зависимость
Пусть задано отношение R, которое содержит
наборы атрибутов A и B. В отношении R B функционально
зависит от A и А функционально определяет В, тогда и только тогда, когда каждое значение проекции R[А] в любой момент времени связано точно с одним значением проекции R[В]. Эта ФЗ обозначается следующим образом: R.А → R.В. (или .А → В). Набор атрибутов А называют детерминантом для набора атрибутов В.Формальное определение функциональной зависимости (FD):
Наличие функциональной зависимости является свойством схемы, а не того или иного экземпляра отношения, и отражает семантику моделируемой предметной области.
Слайд 9Monday, August 12, 2019
Ключи
Набор К атрибутов отношения R называется возможным
ключом отношения R, если верно, что:
все атрибуты отношения R функционально
зависит от К;ни один атрибут из набора К не может быть удален без нарушения свойства (а).
Утверждение: Любое отношение имеет возможный ключ.
Набор К атрибутов отношения R называется суперключом отношения R, если все атрибуты R функционально зависит от К.
Слайд 10Monday, August 12, 2019
Свойства функциональных зависимостей
Свойства
1), 2), 3) составляют
систему
аксиом Армстронга
Слайд 11Monday, August 12, 2019
Логические следствия зависимостей
Пусть в отношении R имеется
множество функциональных зависимостей F и конкретная зависимость А → С,
которая не входит в F. Зависимость А → С логически следует из зависимостей F, если она может быть выведена из F с помощью аксиом функциональных зависимостей. Также говорят, что зависимость А → С выводима из F.Например, если в R(A, B, C) и множество F состоит из А → В, то из нее логически следуют (выводимы) следующие зависимости:
(А, С) → В - применяется свойство продолжения;
(А, С) → (В, С) - применяется свойство пополнения.
Слайд 12Monday, August 12, 2019
Замыкание, полнота, эквивалентность и минимальное покрытие FD
Пусть
в отношении R имеется множество FD F. Множество всех FD,
являющихся следствием (выводимыми) из F, называется (логическим) замыканием F, которое обозначается через F+. Очевидно, что F ⊆ F+ и F+ = F++.Множество FD F образует полное семейство зависимостей, если F = F+.
Множества FD F и G (логически) эквивалентны, если F+ = G+.
Пусть задано множество FD F. Говорят, что множество FD G образует базис зависимостей F или, то же самое, образует минимальное покрытие F, если G является таким минимальным подмножеством F, что G+ =F+.
Слайд 13Monday, August 12, 2019
FD и сущности предметной области
Тезис. Если в
ПО существует FD А → В, то в этой ПО
имеется класс сущностей, определенных на атрибутах (А,В) , причем А является ключом сущностей этого класса, а В – обычный их атрибут.Если А → В1, А → В2, …, А → Вn, то существует класс сущностей с атрибутами (А, В1,…,Вn), где А – ключ, а В1,…, Вn – обычные атрибуты.
Этот тезис дает формальную основу выявления сущностей предметной области.
Слайд 14Monday, August 12, 2019
Неполная (частичная) функциональная
зависимость и вторая нормальная
форма (2NF)
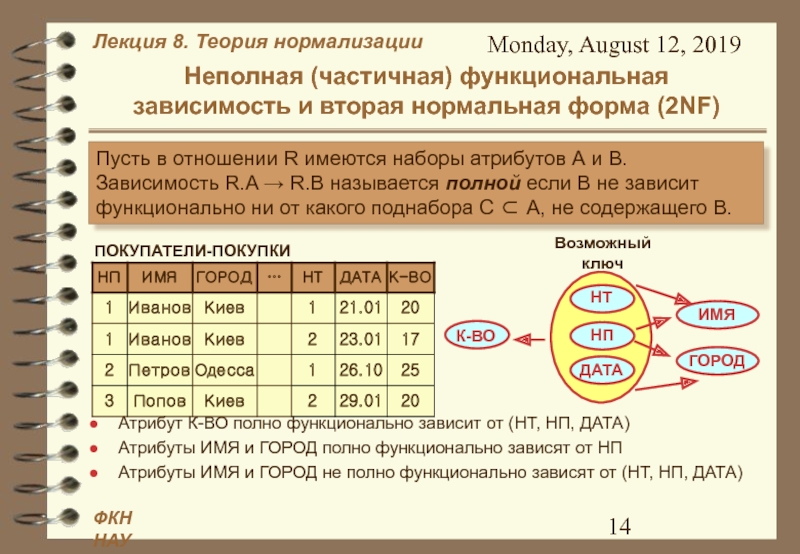
Пусть в отношении R имеются наборы атрибутов А и
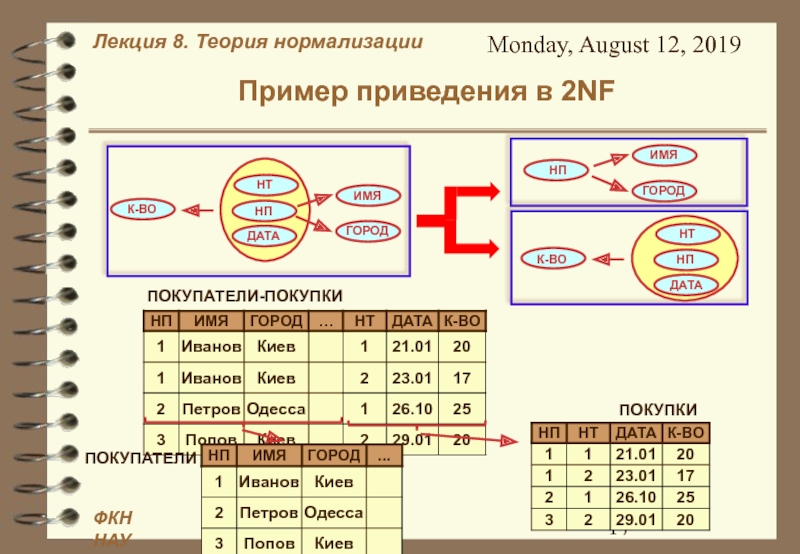
В. Зависимость R.A → R.B называется полной если В не зависит функционально ни от какого поднабора С ⊂ А, не содержащего В.ПОКУПАТЕЛИ-ПОКУПКИ
Атрибут К-ВО полно функционально зависит от (НТ, НП, ДАТА)
Атрибуты ИМЯ и ГОРОД полно функционально зависят от НП
Атрибуты ИМЯ и ГОРОД не полно функционально зависят от (НТ, НП, ДАТА)
Слайд 15Monday, August 12, 2019
Аномалии вставки, удаления, замены
при наличии неполной
FD
ПОКУПАТЕЛИ-ПОКУПКИ
Аномалия обновления. При необходимости изменения города покупа-
теля следует помнить,
что сведения о покупателе могут повторяться.Аномалия вставки. При необходимости включения сведений о новом покупателе (Игнатов) это можно будет сделать только тогда, когда он сделает первую покупку.
Аномалия удаления. При удалении сведений о покупке (Петрова) удаляются сведения и о его покупателе. Если же эти сведения о покупателе в единственном числе, то они теряются в базе данных
Слайд 16Monday, August 12, 2019
Вторая нормальная форма (2NF)
Отношение находится во
второй нормальной форме, если оно находится в первой нормальной форме
и все его неключевые атрибуты функционально полно зависят от возможного ключа.Теорема (Хита). Отношение R с наборами атрибутов А, В, С ,
где R.A → R.B, является естественным соединением проекций
R[A, B] и R[A, C].
Алгоритм приведения к 2NF. Пусть R имеет множество атрибутов M. Если в R имеется неполная FD R.A → R.B неключевого атрибута
B от возможного ключа А, то R разбивается на два отношения:
R1[A, B] и R2[M - B]. Если результирующие отношения все еще не находятся в 2NF, то к ним опять применяется этот алгоритм.
Такое разбиение называется бинарной декомпозицией.
Слайд 18Monday, August 12, 2019
Пример приведения в 2NF - итоги
Исходное отношение
содержит информацию о двух сущностях, результирующие – каждое по одной
сущности.Результирующие отношения не содержат аномалий вставки, удаления, замены.
Исходное отношение можно восстановить из результирующих с помощью операции естественного соединения.
При таком разбиении не теряются функциональные зависимости (то есть зависимости исходного и результирующих отношений эквивалентны)
Слайд 19Monday, August 12, 2019
Транзитивная зависимость и 3NF
1) Условие В →
А необходимо, чтобы исключить тривиальную транзитивную зависимость типа следующей:
2) Условия С
⊄ В, В ⊄ А необходимы, чтобы исключить следующие тривиальные транзитивные зависимости:А
С
В
В
А
С
Слайд 20Monday, August 12, 2019
Аномалии вставки, удаления, замены
при наличии транзитивной
зависимости
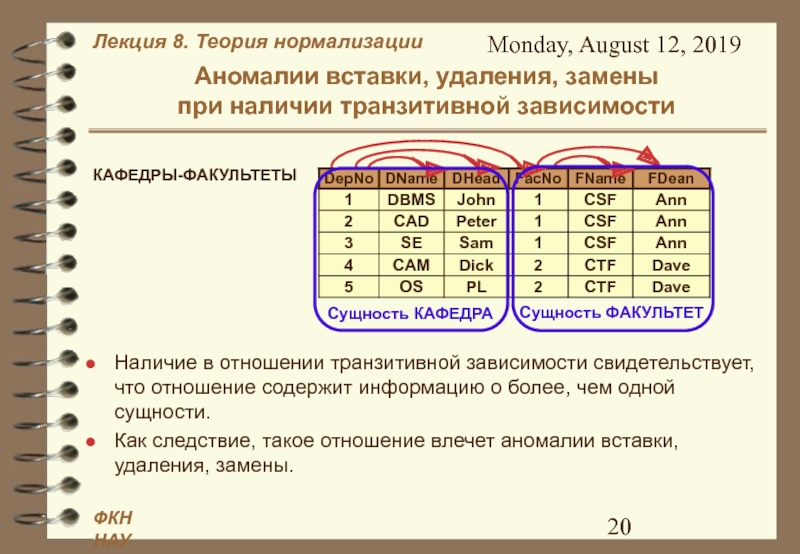
КАФЕДРЫ-ФАКУЛЬТЕТЫ
Сущность КАФЕДРА
Сущность ФАКУЛЬТЕТ
Наличие в отношении транзитивной зависимости свидетельствует, что отношение
содержит информацию о более, чем одной
сущности.Как следствие, такое отношение влечет аномалии вставки, удаления, замены.
Слайд 21Monday, August 12, 2019
Третья нормальная форма (3NF)
Отношение находится в третьей
нормальной форме, если оно находится во второй нормальной форме и
не содержит транзитивных зависимостей непервичных атрибутов от возможных ключей.Другими словами все непервичные атрибуты должны функционально зависеть только от возможных ключей.
Алгоритм приведения к 3NF. Пусть задано отношение R со множеством атрибутов M. Если в R имеется транзитивная функциональная зависимость R.A → R.B и R.В → R.С неключевого атрибута С от возможного ключа А, то отношение R разбивается на следующие два отношения: R[В, С] и R[M - С]. Если результирующие отношения все еще не находятся в третьей нормальной форме, то к ним опять применяется этот алгоритм.
Слайд 23Monday, August 12, 2019
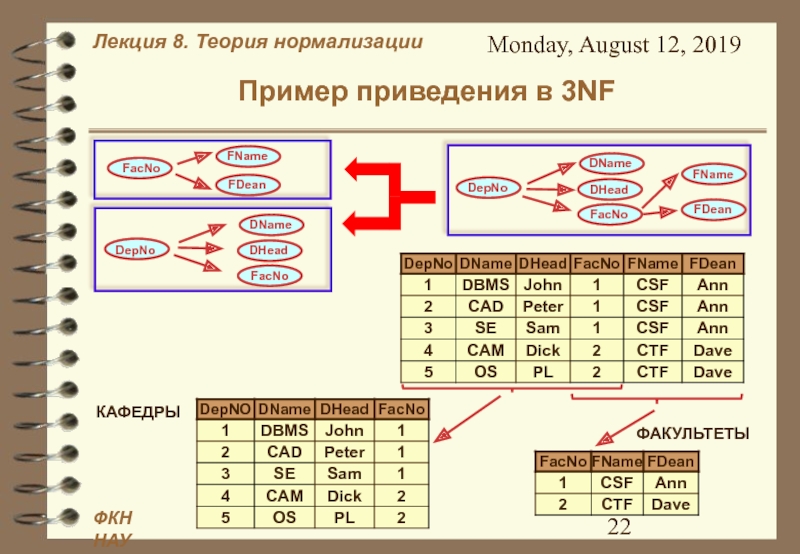
Пример приведения в 3NF - итоги
Результаты те
же, что и при приведении в 2NF:
Исходное отношение содержит информацию
о двух
сущностях, результирующие – каждое по одной
сущности.
Результирующие отношения не содержат аномалий вставки, удаления, замены.
Исходное отношение можно восстановить из результирующих с помощью операции естественного соединения.
При таком разбиении не теряются функциональные зависимости (то есть зависимости исходного и результирующих отношений эквивалентны)
Слайд 24Monday, August 12, 2019
Усиленная 3NF (S3NF)
3NF требует отсутствия транзитивной
зависимости именно непервичных атрибутов, а не всех атрибутов отношения. Усиленная
3NF требует отсутствия транзитивной зависимости для ВСЕХ атрибутов отношения.Отношение находится в усиленной третьей нормальной форме, если оно находится во второй нормальной форме и не содержит транзитивных зависимостей ВСЕХ атрибутов от возможных ключей.
Это отношение находится в 3NF, но содержит информацию о двух сущностях и поэтому обладает аномалиями
Слайд 25Monday, August 12, 2019
Приведение в S3NF
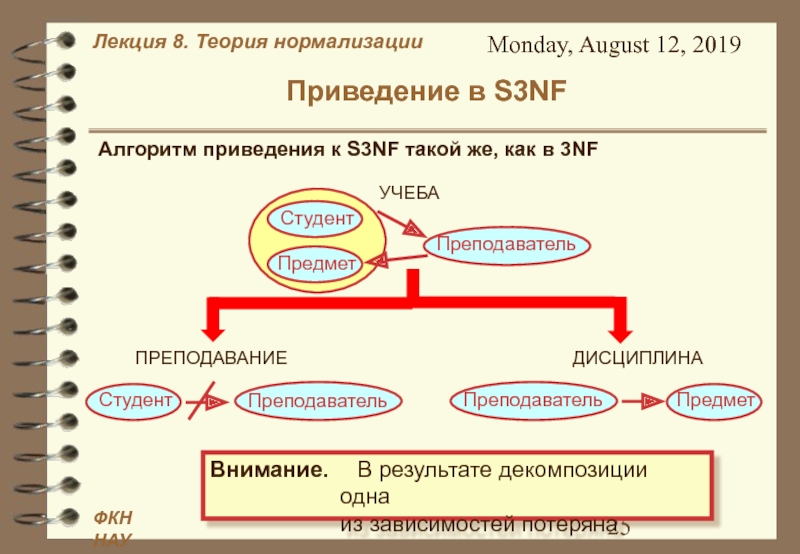
Алгоритм приведения к S3NF
такой же, как в 3NF
Студент
Предмет
Преподаватель
УЧЕБА
Студент
Преподаватель
Преподаватель
Предмет
ПРЕПОДАВАНИЕ
ДИСЦИПЛИНА
Внимание. В результате декомпозиции одна
из зависимостей
потеряна Слайд 26Monday, August 12, 2019
Нормальная форма Бойса-Кодда (BCNF)
Отношение R находится в
нормальной форме Бойса-Кодда, если любой детерминант является суперключом.
Утверждение. Усиленная третья нормальная
форма и нормальная форма Бойса-Кодда эквивалентны Слайд 27Monday, August 12, 2019
Многозначная зависимость и 4NF
Тезис: Если в
предметной области отсутствует какая-либо непос- редственная связь между атрибутами А
и В, а нам по тем или иным причинам необходимо зафиксировать такую связь в отношении, то единственным корректным решени-ем является установление, что все значения атрибута А связаны со всеми значениями атрибута В, и наоборот.УЧЕБА
Слайд 28Monday, August 12, 2019
Определение многозначной зависимости
(MVD)
Пусть задано отношение R
с атрибутами (или наборами атрибутов) А, В, С. Говорят, что
существует многозначная зависимость В от А (или А многозначно определяет В), и это обозначается как А →→ В, если при заданных значениях атрибутов из А существует множество связанных значений атрибутов из В и это множество В-значений не зависит от значений атрибутов из С .Пример: В отношении УЧЕБА имеются следующие MVD:
Пусть задано отношение R(A,B). MVD А →→ ∅ и А →→ В называются тривиальными так как они присутствуют во любых отношениях .
Предмет →→ Преподаватель
Предмет →→ Учебник
Слайд 29Monday, August 12, 2019
Аксиомы MVD
Пусть R состоит из атрибутов (или
набора атрибутов) А, В, С.
MVD обладают следующими аксиомами:
1) Аксиома дополнения
Если А
→→ В, то А →→ С2) Аксиома пополнения
Если А →→ В и V ⊆ W, то (А, W) →→ (В, V)
3) Аксиома транзитивности
Если А →→ В и В →→ С, то А →→ С – В
Слайд 30Monday, August 12, 2019
Аксиомы связи FD и MVD
1) Аксиома репликации
Существуют
следующие две аксиомы, которые связывают
многозначные и функциональные зависимости.
Если А
→ В, то А →→ В2) Аксиома соединения
Если А →→ В и Z ⊆ B, и для некоторого W,
непересекающегося с B имеем W → Z, то
A → Z
Слайд 31Monday, August 12, 2019
Дополнительные свойства MVD
1) Объединение
Если А →→ В
и А →→ С, то А →→ (В, С)
Если А
→→ В и (W, В) →→ Z , то (W, А) →→ Z – (W, В)
2) Псевдотранзитивность
3) Смешанная псевдотранзитивность
Если А →→ В и (А,В) →→ С, то А →→ (С - В)
4) Пересечение и разность
Если А →→ В и А →→ С,
то А →→ В ∩ С, А →→ В – С, А →→ С – В
Слайд 32Monday, August 12, 2019
Четвертая нормальная форма (4NF)
Отношение R находится в
четвертой нормальной форме (4NF), если из существования в нем нетривиальной
MVD X →→ Y (где Y ⊄ Х) следует, что Х является суперключом отношения R.Утверждение. Пусть отношение R состоит из атрибутов (или множеств атрибутов) А, В, С. Зависимость А →→ В имеет место в R тогда и только тогда, когда R = R[A, B] * R[A, C].
Слайд 33Monday, August 12, 2019
Приведение в 4NF и встроенные MVD
Алгоритм приведения
к 4NF. Пусть задано отношение R с атрибутами А, В,
С, и имеется многозначная зависимость R.A →→ R.B Тогда отношение R декомпозируются на следующие два отношения: R[A, B] и R[B, С].Если результирующие отношения все еще не находятся в 4NF, то к ним опять применяется этот алгоритм.
Многозначная зависимость называется встроенной, если она отсутствует в самом отношении, но существует в его проекциях по некоторым атрибутам.
Слайд 34Monday, August 12, 2019
Зависимость по соединению (JD) и
пятая нормальная
форма
Пусть R является отношением с атрибутами (множествами атрибутов) А1, А2,
…, Аn. Отношение R обладает зависимостью по соединению (JD) относительно А1, А2, …, Аn, что обозначается как *(А1, А2,…, Аn), если отношение R равно естественному соединению его проекций на А1, А2, …, Аn, то есть:R = πA1(R)*πA2(R)*... * πAn(R) ⇔ R = R[A1] * R[A2]*…*R[An])
JD является тривиальной, если один из наборов атрибутов Ai совпадает со множеством всех атрибутов отношения R.
JD является следствием возможных ключей отношения R, если все Ai (1 ≤ i ≤ n) являются суперключами R.
Слайд 35Monday, August 12, 2019
Связь зависимостей по соединению (JD) и
многозначных
зависимостей (MVD)
Каждая JD вида *(A, B) в отношении со схемой
R(A,B), где А и В -
множества атрибутов, является эквивалентной MVD А ∩ В →→ А и
А ∩ В →→ В. (Любая MVD является JD, но не наоборот!!!)Однако, существуют JD, которые не эквивалентны никакой MVD. Так, например, если в отношении R = (A, B, C) имеется JD *((A,B), (B, C), (A,C)), то она не эквивалентна никакой MVD. Пример:
На приведенном примере отношение содержит JD *((A,B), (B, C), (A,C)), что можно проверить, вычислив: πA1(R) * πA2(R) *... * πAn(R) .
Однако никакой нетривиальной MVD в нем нет.
В этом можно убедиться, проверив, что ни одна из следующих зависимостей не удовлетворяется:
A →→B, A →→C, B →→A, B →→C, C →→A,C →→B.
Слайд 36Monday, August 12, 2019
Пятая нормальная форма - 5NF
Отношение R находится
в пятой нормальной форме (5NF) тогда и только тогда, когда
для каждой его нетривиальной JD *(А1, А2,…, Аn) все множества атрибутов Ai являются суперключами R.Эта нормальная форма также получила название:
проекционно-соединительной нормальной формы (PJNF).
Утверждение. Так как любая многозначная зависимость является также и зависимостью по соединению, то любое отношение, находящееся в 5NF (PJNF), также находится и в 4NF.
Введение 5NF аргументируется тем, что никакая n-арная
декомпозиция отношения не может быть представлена в виде
последовательности бинарных декомпозиций.
Слайд 37Monday, August 12, 2019
Пример отношения в 5NF
Пусть задано отношение TBS(TCH,
BOK, SBJ), которое предназначено для хранения следующей информации:
какие книги
какими преподавателями используются; какие книги в каких дисциплинах используются;
какие дисциплины какими преподавателями читаются.
Тот факт, что в отношении занесена следующая информация:
Резниченко использует в своих лекциях книгу «Язык SQL»,
Книга «Язык SQL» используется в предмете ОБДиБЗ» и
Резниченко читает лекции по предмету ОБДиБЗ
еще не свидетельствует, что «Резниченко использует книгу Язык SQL для чтения лекций по предмету ОБДиБЗ»
Отношение TBS находится в 5NF хотя бы потому, что в ней нет JD.
Слайд 38Monday, August 12, 2019
Пример отношения, нарушающего 5NF,
и приведения в
5NF
Если же в отношении TBS действует дополнительное правило
(в качестве
бизнес-правила целостности): то в TBS имеется JD *((TCH, BOK), (BOK, SBJ), (TCH, SBJ)) и это отношение не находится в 5NF, так как в нем единственным ключом является весь набор атрибутов, то есть (TCH, BOK, SUBJ).
В этом случае TBS приводится в 5NF следующим образом:
«Из фактов:
- преподаватель t использует в лекциях книгу b,
- книга b используется в дисциплине s и
- преподаватель t читает лекции по дисциплине s
следует, что преподаватель t использует книгу b для чтения лекций по дисциплине s»,
TBS(TCH, BOK, SBJ) ⇒TB(TCH,BOK), BS(BOK, SBJ), TS(TCH, SBJ)
Слайд 39Monday, August 12, 2019
Пример отношения, нарушающего 4NF,
и приведения в
4NF
Если же в отношении TBS действует дополнительное правило
(в качестве
бизнес-правила целостности): то в TBS имеется JD *((TCH, BOK), (TCH, SBJ)) или, что то же самое, имеются MVD TCH →→ BOK, TCH →→ SBJ, и это отношение не находится не только в 5NF, но и в 4NF.
В этом случае TBS приводится в 4NF (и, более того, в 5NF) следующим образом:
«Из фактов:
- преподаватель t использует в лекциях книгу b,
- преподаватель t читает лекции по дисциплине s
следует, что преподаватель t использует книгу b для чтения лекций по дисциплине s»,
TBS(TCH, BOK, SBJ) ⇒TB(TCH,BOK), TS(TCH, SBJ)
Слайд 40Monday, August 12, 2019
Проектирование схемы
реляционной модели данных
Формальная постановка задачи
проектирования реляционной схемы
Декомпозиция схемы реляционного отношения
Эквивалентность отношений
Декомпозиция без потери
(с сохранением) данныхДекомпозиция без потери (с сохранением) зависимостей
Эквивалентность нормальных форм
Критерий качества реляционной схемы
Слайд 41Monday, August 12, 2019
Формальная постановка задачи
проектирования реляционной схемы
В этом
определении следует уточнить:
процедуру представления отношений в виде совокупности других;
понятие эквивалентности
схем отношений;критерий качества схемы отношений.
Тезис об универсальном отношении. Вся ПО может быть представле-на в виде универсального отношения, содержащего все атрибуты ПО.
Задача проектирования. Реляционную схему S0, содержащую схему универсального отношения R:
S0 = {R =
где U – множество атрибутов, а G – множество зависимостей,
необходимо эквивалентно преобразовать в схему SD,
представленную в виде совокупности отношений R1,…, Rn:
SD = {Ri =
которая была бы в некотором смысле лучше схемы S0.
Слайд 42Monday, August 12, 2019
Декомпозиция схемы
реляционного отношения
Декомпозицией отношения R со
схемой R(M) называется процедура разбиения R на множество отношений R1,
R2,…, Rn со схемами R1(M1),…, Rn(Mn), которая удовлетворяет следующим требованиям:М1 ∪ М2 ∪ … ∪ Мn = М. Другими словами, любой атрибут из R должен содержаться в по крайней мере одном из отношений Ri и все Ri должны быть определены на атрибутах R.
Все отношения Ri (1 ≤ i ≤ n), являются проекциями исходного отношения R по атрибутам, содержащимся в Ri, то есть Ri(Mi) = πMi(R)
Декомпозиция обладает свойством соединения без потерь, если R является естественным соединением R1, R2,…, Rn , то есть
R= R1 * R2 *…* Rn
Итак, декомпозиция – единственная операция,
используемая при разбиении схем отношений
Слайд 43Monday, August 12, 2019
Эквивалентность схем отношений
по зависимостям
Эквивалентность по зависимостям.
Две совокупности отношений эквивалентны по зависимостям, если они определены на
одних и тех же атрибутах, и в них сохранены все зависимости данных (функциональные и многозначные).Если исходной и результирующей схемами являются S0 и SD, то эквивалентность по зависимостям означает следующее:
Где U, Ui – атрибуты S0 и SD, а G, Gi – зависимости S0 и SD.
Слайд 44Monday, August 12, 2019
Эквивалентность отношений по данным
Эквивалентность по данным. Две
совокупности отношений эквивалентны по данным, если естественные соединения отношений каждой
из совокупностей дают идентичные отношения.Если исходной и результирующей схемами являются S0 и SD, то экви-валентность по данным означает, что такое разбиение производится декомпозицией, обладающей свойством соединения без потерь.
Как добиться, чтобы декомпозиция обладала этим свойством?
Утверждение. Если R1(U1) R2(U2) являются декомпозицией R(U)
с сохранением функциональных и/или многозначных зависимостей, то эта декомпозиция обеспечивает соединение без потерь тогда и только тогда, когда:
U1 ∩ U2 → (или →→) U1 – U2
либо
U1 ∩ U2 → (или →→) U2 – U1
Слайд 45Monday, August 12, 2019
Эквивалентность нормальных форм
Свойство соединения без потерь не
всегда гарантирует сохранение зависимостей.
Аналогично, не каждое разложение, сохраняющее зависимости,
обладает свойством соединения без потерь.Эквивалентность нормальных форм.
Декомпозиция универсального отношения вплоть до 3NF сохраняет эквивалентность по данным и по зависимостям.
При приведении универсального отношения к BCNF сохраняется эквивалентность по данным, но теряется эквивалентность по зависимостям.
Слайд 46Monday, August 12, 2019
Критерий качества реляционной схемы
Рассмотрим теперь вопрос, что
значит одна схема
отношений лучше другой.
Здесь можно говорить о
критериях независимости представ-
ления связей и степени неизбыточности данных и, как след-
ствие, об отсутствии возможных аномалий манипулирования
данными. Фактически эти качества можно оценить характеристиками нормальных форм отношений. Чем в более высокой" нормальной форме находится совокупность отношений, тем более независимо представлены в них функциональные и многозначные зависимости.