Слайд 1Теория вероятностей
Лекции по математике
Слайд 2И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Рекомендуемая литература
Кремер
Н.Ш. Теория вероятностей и математическая статистика. - М.: Банки и
биржи, ЮНИТИ, 2001 .
Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: В.Ш., 2002 .
Тимошина И.Р. Электронный конспект лекций по теории вероятностей. ВФ СПбГУСЭ, 2008.
Слайд 3И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Содержание
Зависимые и
независимые случайные величины
Условные законы распределения составляющих системы дискретных случайных величин
Условные
законы распределения составляющих системы непрерывных случайных величин
Слайд 4И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Зависимые и
независимые случайные величины
Будем называть две случайные величины X и Y
независимыми, если закон распределения одной случайной величины не зависит от того, какое значение приняла другая случайная величина.
Сформулируем необходимые и достаточные условия независимости случайных величин.
Слайд 5И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Теорема
Для того
чтобы случайные величины X и Y были независимы, необходимо и
достаточно, чтобы функция распределения системы F(x,y) была равна произведению функций распределения составляющих:
Слайд 6И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Следствия
Следствие 1.
Для того чтобы дискретные случайные величины X и Y были
независимы, необходимо и достаточно, чтобы выполнялось условие:
Слайд 7И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Следствия
Следствие 2.
Для того чтобы непрерывные случайные величины X и Y были
независимы, необходимо и достаточно, чтобы плотность совместного распределения системы была равна произведению плотностей распределения составляющих:
Слайд 8И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Пример 1.
Закон распределения системы
дискретных случайных величин задан таблицей:
Исследовать, являются
ли величины X и Y
независимыми.
Слайд 9И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Решение. Закон
распределения величины X
имеет вид:
Закон распределения величины Y имеет вид:
Слайд 10И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Если бы
величины X и Y были независимыми,
то закон распределения системы
таких величин
имел бы следующий вид:
Ответ. Величины X и Y являются зависимыми.
Слайд 11И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Пример 2.
Двумерная непрерывная случайная
величина задана плотностью совместного
распределения
в квадрате
Вне квадрата
f(x,y)=0.
Доказать, что величины X и Y независимы.
Слайд 12И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Решение. Найдём
плотности распределения
составляющих, воспользовавшись формулами:
Аналогично получим
Слайд 13И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Так как
,
то величины X и Y независимы.
Слайд 14И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Условные законы
распределения
Известно, что если события А и В зависимы, то условная
вероятность события В отличается от его безусловной вероятности. Формула для вычисления условной вероятности:
Слайд 15И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Условные законы
распределения системы дискретных величин
Рассмотрим систему дискретных случайных величин (X,Y).
Если зафиксировать
значение одной из величин, например, Y=yj, то полученное распределение случайной величины X называется условным распределением при условии, что Y=yj.
Слайд 16И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Условные законы
распределения системы дискретных величин
Вероятности
будут условными вероятностями событий
Из формулы
для вычисления условной вероятности следует, что
Слайд 17И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Условные законы
распределения системы дискретных величин
Аналогично условное распределение величины Y задаётся с
помощью условных вероятностей
Слайд 18И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
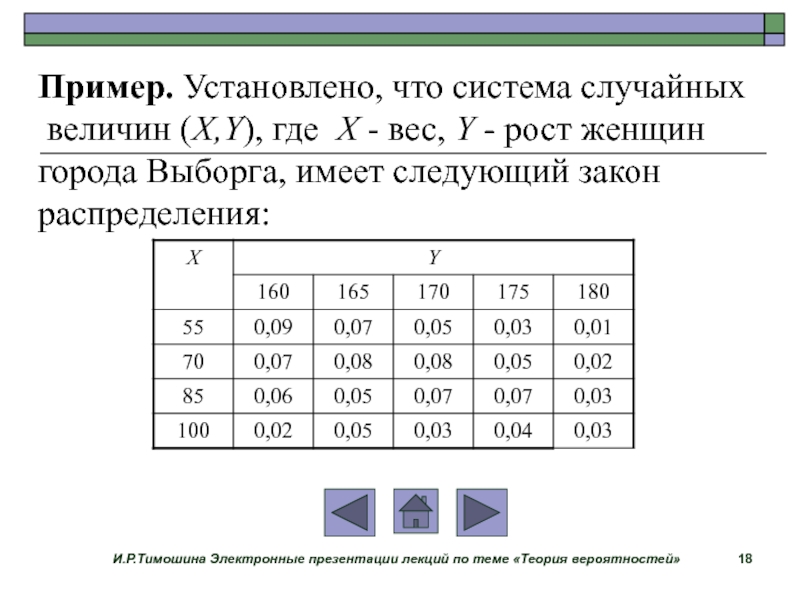
Пример. Установлено,
что система случайных
величин (X,Y), где X - вес, Y
- рост женщин
города Выборга, имеет следующий закон
распределения:
Слайд 19И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Найти условный
закон распределения роста
женщин Y, имеющих вес X=70 кг.
Решение.
P(X=70)=0,07+0,08+0,08+0,05+0,02=0,3
Слайд 20И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Условный закон
распределения роста женщин:
Безусловный закон распределения роста женщин:
Слайд 21И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Сравнение условного
и безусловного закона
распределения случайной величины Y говорит
о том,
что рост и вес женщин являются
зависимыми случайными величинами.
Слайд 22И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Условные законы
распределения системы непрерывных величин
Пусть (X,Y)- непрерывная двумерная случайная величина, f(x,y)
– плотность совместного распределения величин, f1(x) и f2(y) – плотности распределения X и Y соответственно.
Слайд 23И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Условные законы
распределения системы непрерывных величин
Условная плотность распределения
величины X при условии, что
величина Y=y, вычисляется по формуле:
Условная плотность распределения
величины Y при условии, что величина X=x, вычисляется по формуле:
Слайд 24И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Условные законы
распределения системы непрерывных величин
Если известна плотность совместного распределения f(x,y), то
Слайд 25И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Пример. Система
случайных величин (X,Y)
распределена по закону:
.
Найти коэффициент а. Исследовать систему на
зависимость-независимость. Найти f1(x) и f2(y).
Решение.
1. Найдём коэффициент а из условия:
Слайд 26И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
Следовательно,
2.
Функции распределения:
Слайд 27И.Р.Тимошина Электронные презентации лекций по теме «Теория вероятностей»
3.
,
т.е. величины X и Y являются независимыми.