Слайд 1Термодинамика и статистическая физика
Слайд 2 Лекция № 5
Фазовые переходы.
1. Понятие о
фазах вещества. Условия рав- новесия фаз.
2. Фазовые переходы первого
рода (плавле- ние, кристаллизация, испарение, конден- сация, возгонка, сублимация).
3. Уравнение Клапейрона-Клаузиуса. Фазо- вые диаграммы. Тройная точка. Понятие о фазовых переходах второго рода.
Слайд 3 Фазой называется термодинамически равновесное состояние
вещества, отличающееся по физическим свойствам от других возможных равновесных состояний
того же вещества, т.е. совокупность однородных, одинаковых по своим свойствам частей системы.
Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза - вода; газообразная фаза - смесь воздуха с водяными парами.
Если в воду бросить кусочки льда, то эта система станет трехфазной, в которой лед является твердой фазой.
Слайд 4Переход вещества из одной фазы в другую - фазовый переход
- всегда связан с качественными изменениями свойств вещества. Примером фазового
перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую). Различают фазовые переходы двух родов.
Часто понятие "фаза" употребляется в смысле агрегатного состояния, однако надо учитывать, что оно шире, чем понятие "агрегатное состояние". В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по своим свойствам, составу и строению (лед, например, встречается в пяти различных модификациях – фазах).
Слайд 5 Фазовый переход I рода (например, плавление, кристаллизация, испарение, конденсация,
возгонка, сублимация) сопровождается поглощением или выделением теплоты, называемой теплотой
фазового перехода.
Фазовые переходы I рода характеризуются постоянством температуры, но изменениями энтропии и объема (скачком изменяется внутренняя энергия и плотность).
Слайд 6 Примером процесса образования кристал-лов из паров (субли-мация) является образование
инея и снежинок из водяных паров воздуха.
Кипение – это
парообразование, которое происходит в объеме всей жидкости и при постоянной температуре.
Слайд 7 На рисунке представлен график зависимости температуры льда от
полученной теплоты. Q1 – теплота, полученная льдом при
нагревании;
Q2 – теплота, полученная льдом при плавлении;
Q3 – теплота, полученная растаявшим льдом при нагревании;
тангенс углов наклона φ1 и φ2 пропорционален величинам теплоемкости льда и воды.
Слайд 8 При плавлении телу нужно сообщить некоторое количество
теплоты, чтобы вызывать разрушение кристаллической решетки. Подводимая при плавлении теплота
идет не нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. При таких переходах - из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние - степень беспорядка увеличивается, т.е. согласно второму началу термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет.
Слайд 9 Фазовые переходы, не связанные с
поглощением или выделением теплоты и изменением объема, называются фазовыми переходами
II рода.
Эти переходы характеризуются постоянством объема и энтропии, но скачкообразным изменением теплоемкости.
Общая трактовка фазовых переходов II рода предложена Л.Д. Ландау. Согласно Ландау, фазовые переходы II рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода.
Слайд 10Ландау Лев Давидович
( 1908 – 1968
) –
выдающийся советский физик-
теоретик, академик, лауреат
Нобелевской премии ( 1962
г.)
Он был избран членом Королев-
ской датской академии наук
(1951), Нидерландской академии (1956), Британское физическое общество (1959) и Королевского общества Лондона (1960). Также в 1960 он был избран в США Национальной академии наук и Американской академии искусств и наук. Он получил премию Фрица Лондона в 1960 и в том же году Макса Планка.
Слайд 11 Примерами фазовых переходов II рода являются:
1)
переход ферромагнитных веществ (железа, кобальта, никеля) при определенных давлении и
температуре в парамагнитное состояние;
2) переход металлов и некоторых сплавов при температуре, близкой к 0 К, в сверхпроводящее состояние, характеризуемое скачкообразным уменьшением электричес-кого сопротивления до нуля;
3) превращение обыкновенного жидкого гелия (гелий I) при Т=2,9 К в другую жидкую модификацию (гелий II), обладающую свойствами сверхтекучести.
Слайд 12Для анализа устойчивости фазы при фиксированных величинах давления и температуры
вводится новая термодинамическая функция равновесного состояния:
- Термодинамический
потенциал Гиббса
Т.к. - I начало ТД
Слайд 13 Рассмотрим систему, состоящую из 2-х фаз 1 и 2,
которые могут превращаться друг в друга. Пусть m1 – масса
первой, а m2 - масса второй фазы. Обозначим φ1 и φ2 - удельные термодинамичес- кие потенциалы вещества в этих фазах ( ).
Термодинамический потенциал всей системы будет:
Пусть давление и температура системы поддер- живаются постоянными. Тогда при фазовых пре- вращениях величины φ1 и φ2 не будут изменяться:
- условие равнове-
сия фаз
Слайд 14В случае фазового перехода первого рода из фазы 1 в
фазу 2 в точке перехода, определяемой температурой перехода
,
и давлением
первые производные
где s – удельная энтропия,
- удельный объем (объём единицы массы вещества) и
- плотность вещества, испытывают скачок:
,
В процессе всего фазового перехода температура и давление вещества сохраняются постоянными.
Слайд 15В соответствии с первым началом термодинамики скачок удельной энтропии означает,
что фазовые переходы первого рода сопровождаются поглощением или выделением удельной
теплоты
Удельные теплоты прямого и
обратного
фазовых переходов связаны соотношением:
Слайд 16 Рассмотрим следствия условия равновесия фаз и процессы испарения и
конденсации. Каждая точка на плоскости РТ соответствует однородно- му (однофазному)
состоянию вещества- либо жид- кости, либо её пару. Линия ДК представляет урав-
нение , где удельные термодина-мические потенциалы жидкости и пара одинаковы.
Кривая ДК называется
кривой равновесия
жидкости и её насы-
щенного пара или
кривой испарения.
Слайд 17Найдём наклон кривой испарения. Т.е. вычис- лим производную давления насыщенного
пара по температуре dP/dT. При смещении вдоль кривой испарения
. Т.к. , то
, где s1 , υ1 ; s2, υ2 – удельные эн-
тропии и удельные объёмы
1-ой и 2-ой фазы.
то: -уравнение
Клапейрона-
- Клаузиуса
Слайд 18 Это уравнение связывает производную от равновесного давления по
температуре с
удельной теплотой перехода q12 , температурой перехода Т
при давлении Р , разностью удельных объёмов фаз, находящихся в равно-
весии.
-уравнение Клапейрона- Клаузиуса
Слайд 19Уравнение Клапейрона–Клаузиуса позволяет оценить изменение температуры dT фазового перехода, если
давление в системе получило приращение dP:
В общем случае зависимости Т(Р)
дают кривые равновесия фазовой диаграммы. Интересно отметить, что при внешнем давлении >1010 Па вода замерзает при температуре t=100 oC.
Слайд 20Если система является однокомпонентной, т.е. состоящей из химически однородного вещества
или его соединения, то понятие фазы совпадает с понятием агрегатного
состояния.
Одно и то же вещество в зависимости от соотношения между удвоенной средней энергией, приходящейся на одну степень свободы хаотического (теплового) движения молекул, и наименьшей потенциальной энергией взаимодействия молекул может находиться в одном из трех агрегатных состояний: твердом, жидком или газообразном.
Это соотношение, в свою очередь, определяется внешними условиями – температурой и давлением. Следовательно, фазовые превращения также определяются изменениями температуры и давления.
Диаграмма состояния. Тройная точка.
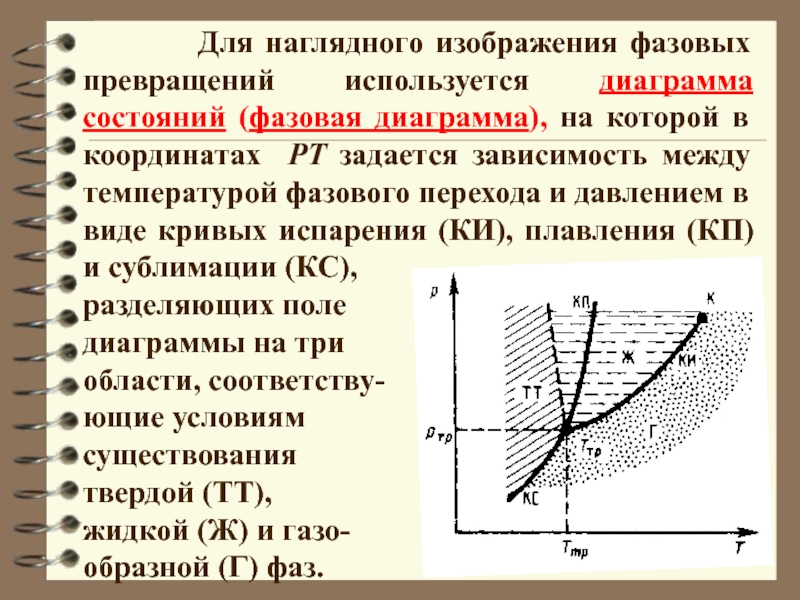
Слайд 21 Для наглядного изображения фазовых превращений
используется диаграмма состояний (фазовая диаграмма), на которой в координатах РТ
задается зависимость между температурой фазового перехода и давлением в виде кривых испарения (КИ), плавления (КП) и сублимации (КС),
разделяющих поле
диаграммы на три
области, соответству-
ющие условиям
существования
твердой (ТТ),
жидкой (Ж) и газо-
образной (Г) фаз.
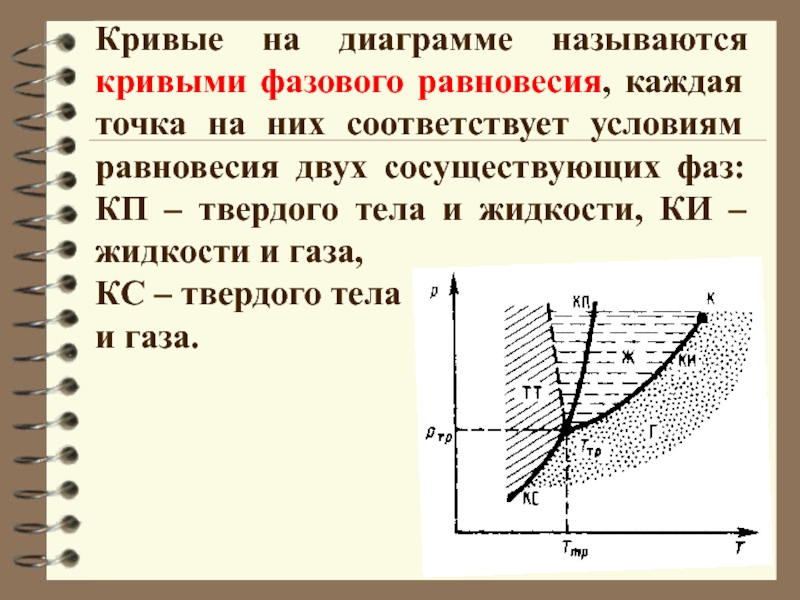
Слайд 22Кривые на диаграмме называются кривыми фазового равновесия, каждая точка на
них соответствует условиям равновесия двух сосуществующих фаз: КП – твердого
тела и жидкости, КИ – жидкости и газа,
КС – твердого тела
и газа.
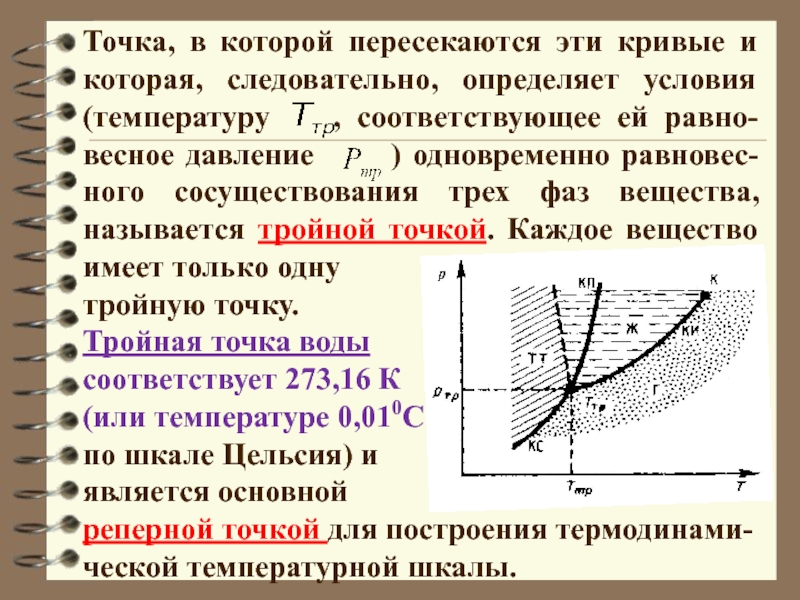
Слайд 23Точка, в которой пересекаются эти кривые и которая, следовательно, определяет
условия (температуру , соответствующее ей равно-весное давление
) одновременно равновес-ного сосуществования трех фаз вещества, называется тройной точкой. Каждое вещество имеет только одну
тройную точку.
Тройная точка воды
соответствует 273,16 К
(или температуре 0,010С
по шкале Цельсия) и
является основной
реперной точкой для построения термодинами-
ческой температурной шкалы.
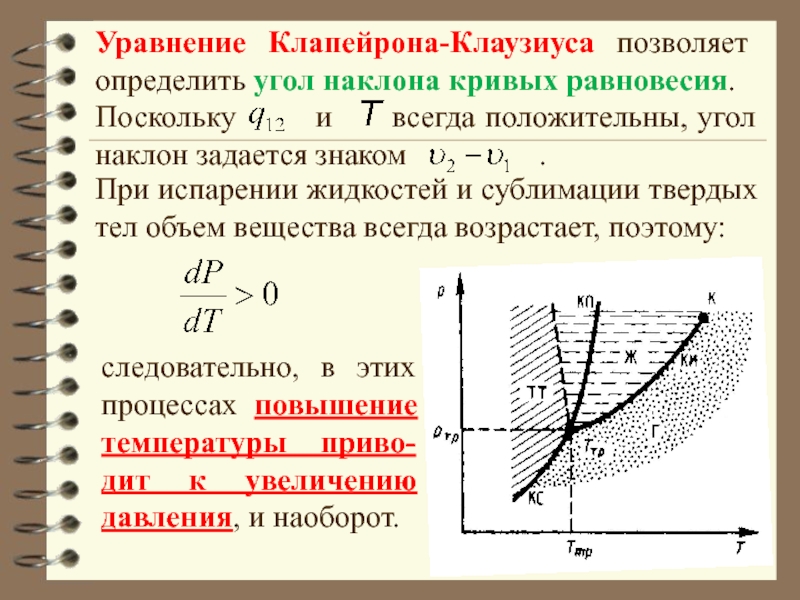
Слайд 24Уравнение Клапейрона-Клаузиуса позволяет определить угол наклона кривых равновесия.
Поскольку
и всегда положительны, угол наклон задается знаком
.
следовательно, в этих процессах повышение температуры приво-дит к увеличению давления, и наоборот.
При испарении жидкостей и сублимации твердых тел объем вещества всегда возрастает, поэтому:
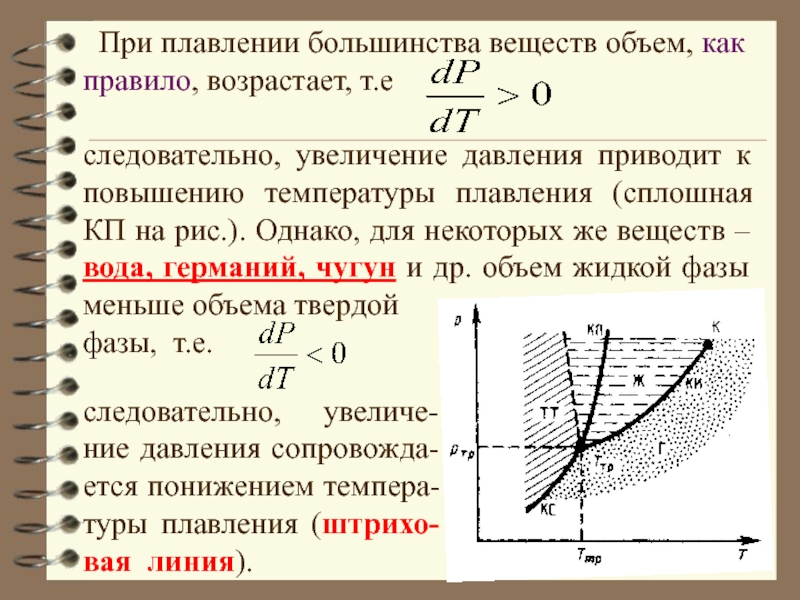
Слайд 25следовательно, увеличение давления приводит к повышению температуры плавления (сплошная КП
на рис.). Однако, для некоторых же веществ – вода, германий,
чугун и др. объем жидкой фазы меньше объема твердой
фазы, т.е.
При плавлении большинства веществ объем, как правило, возрастает, т.е
следовательно, увеличе-ние давления сопровожда-ется понижением темпера-туры плавления (штрихо-вая линия).
Слайд 26Одновременное равновесие сразу трех разных фаз одного вещества требует выполнения
трех равенств:
которые на диаграмме ТР задают три кривых равновесия фаз:
Точка пересечения кривых называется тройной точкой. В тройной точке все три фазы находятся в динамическом равновесии, когда между всеми фазами происходят прямые и обратные переходы, но массы фаз не меняются. Анализ показывает, что равновесие четырех различных фаз невозможно.
Слайд 27Для воды тройная точка характеризуется следующими параметрами:
К и
В случае углекислоты CO2
tтр.т. = -57ºС и Па,
поэтому при атмосферном давлении твердая углекислота (сухой лед) находится в равновесии со своим паром (при температуре t = - 80 ºС). Вследствие этого при комнатной температуре и атмосферном давлении сухой лед лишь испаряется, но не плавится.
Па
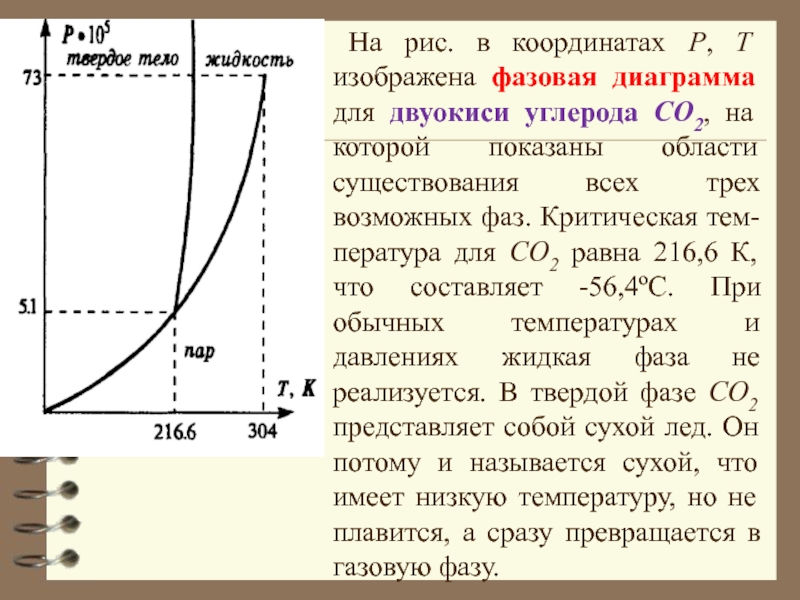
Слайд 28На рис. в координатах P, Т изображена фазовая диаграмма для
двуокиси углерода CO2, на которой показаны области существования всех трех
возможных фаз. Критическая тем-пература для CO2 равна 216,6 К, что составляет -56,4ºС. При обычных температурах и давлениях жидкая фаза не реализуется. В твердой фазе CO2 представляет собой сухой лед. Он потому и называется сухой, что имеет низкую температуру, но не плавится, а сразу превращается в газовую фазу.
Слайд 29Фазовая диаграмма
Кривая OT, соответствующая равновесию
между твердой и газообразной фазами, называется кривой сублимации. Кривая TK
равновесия между жидкостью и паром называется кривой испарения, она обрывается в критической точке K. Кривая TM равновесия между твердым телом и жидкостью называется кривой плавления.
Кривые равновесия сходятся в точке T, в которой могут сосуществовать в равновесии все три фазы. Эта точка называется тройной точкой.
Типичная фазовая диаграмма вещества.
K – критическая точка, T – тройная точка.
Область I – твердое тело, область II – жидкость, область III – газообразное вещество.
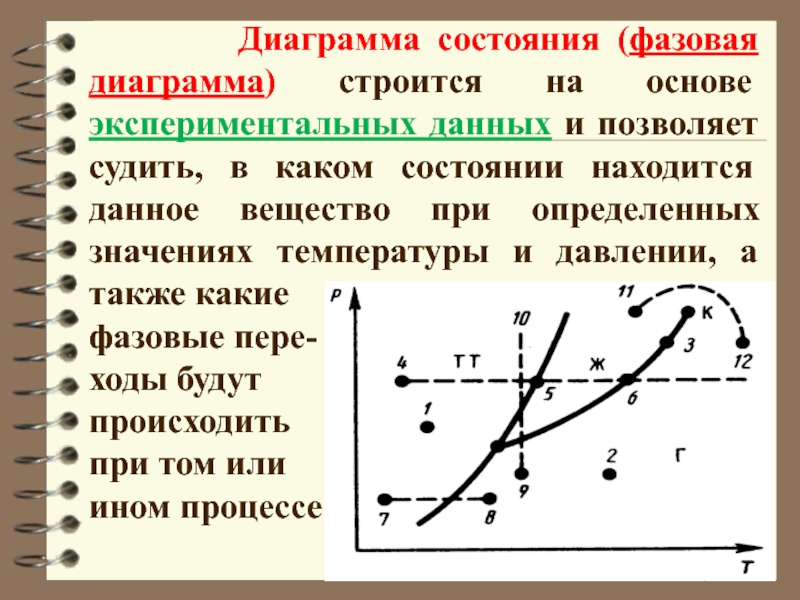
Слайд 30 Диаграмма состояния (фазовая диаграмма) строится
на основе экспериментальных данных и позволяет судить, в каком состоянии
находится данное вещество при определенных значениях температуры и давлении, а также какие
фазовые пере-
ходы будут
происходить
при том или
ином процессе.
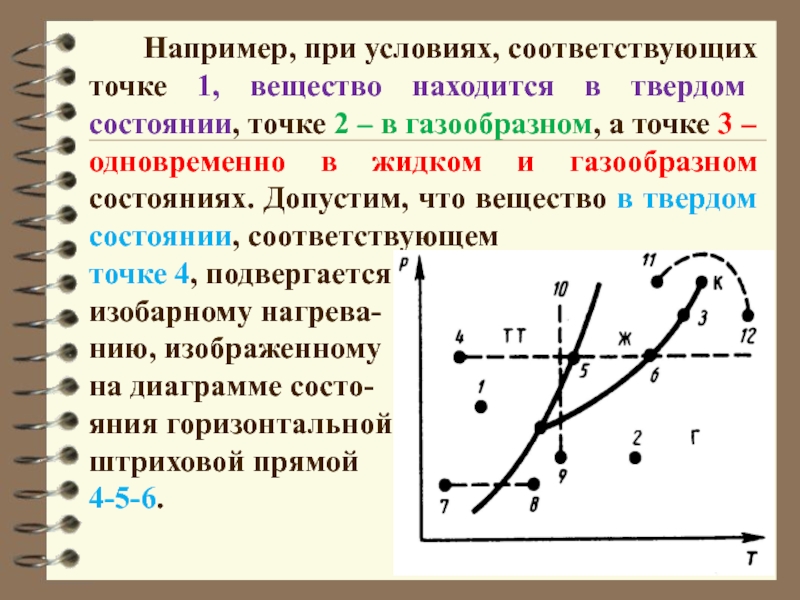
Слайд 31 Например, при условиях, соответствующих точке 1,
вещество находится в твердом состоянии, точке 2 – в газообразном,
а точке 3 – одновременно в жидком и газообразном состояниях. Допустим, что вещество в твердом состоянии, соответствующем
точке 4, подвергается
изобарному нагрева-
нию, изображенному
на диаграмме состо-
яния горизонтальной
штриховой прямой
4-5-6.
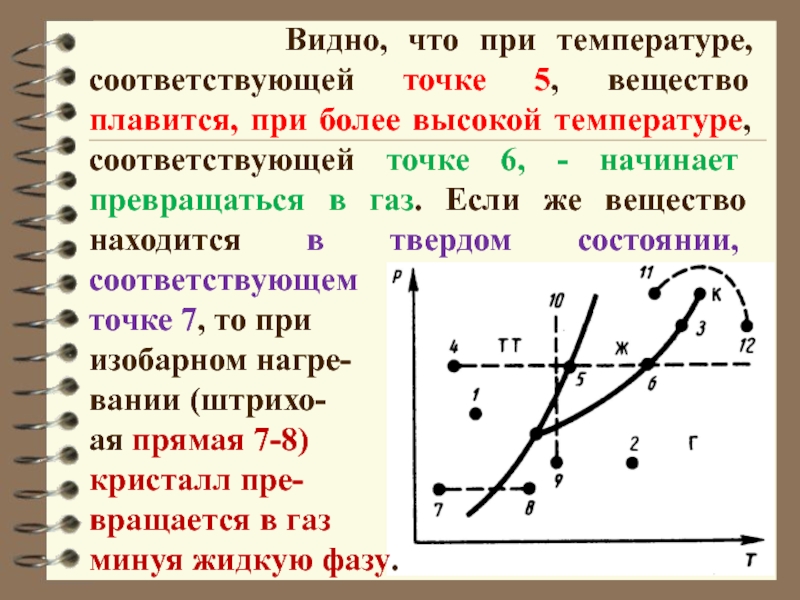
Слайд 32 Видно, что при температуре, соответствующей
точке 5, вещество плавится, при более высокой температуре, соответствующей точке
6, - начинает превращаться в газ. Если же вещество находится в твердом состоянии, соответствующем
точке 7, то при
изобарном нагре-
вании (штрихо-
ая прямая 7-8)
кристалл пре-
вращается в газ
минуя жидкую фазу.
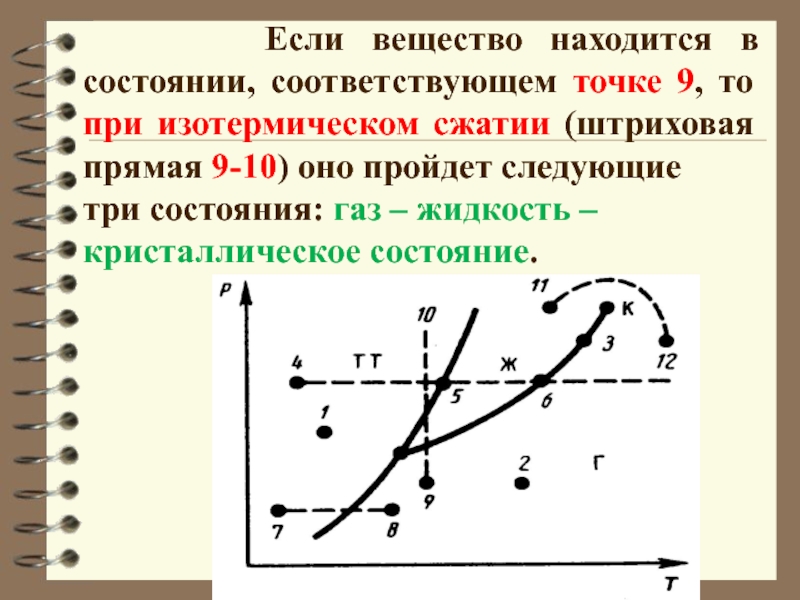
Слайд 33 Если вещество находится в состоянии, соответствующем
точке 9, то при изотермическом сжатии (штриховая прямая 9-10) оно
пройдет следующие
три состояния: газ – жидкость –
кристаллическое состояние.
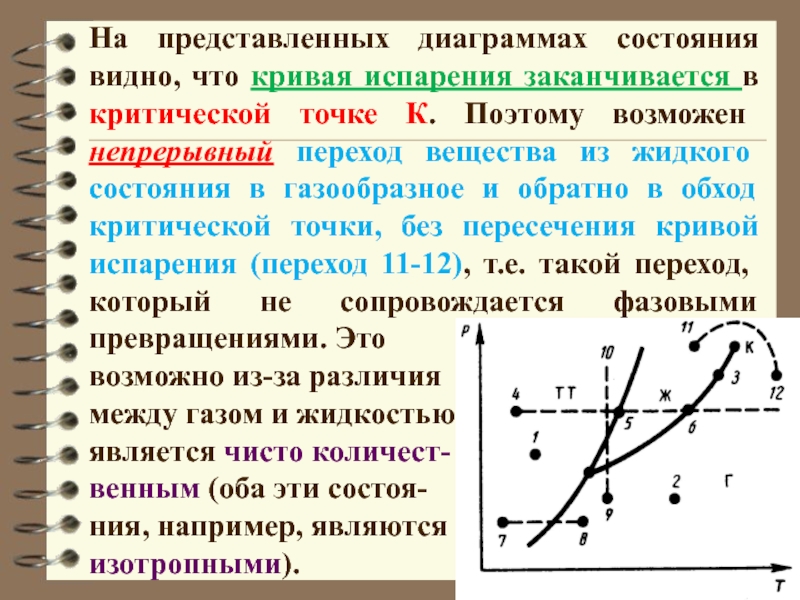
Слайд 34На представленных диаграммах состояния видно, что кривая испарения заканчивается в
критической точке К. Поэтому возможен непрерывный переход вещества из жидкого
состояния в газообразное и обратно в обход критической точки, без пересечения кривой испарения (переход 11-12), т.е. такой переход, который не сопровождается фазовыми превращениями. Это
возможно из-за различия
между газом и жидкостью
является чисто количест-
венным (оба эти состоя-
ния, например, являются
изотропными).
Слайд 35 В критическом состоянии вещества, которое определяется точкой К, исчезают
различия между жидкостью и газом. В области температур
нельзя путем повышения давления превратить газ в жидкость. Если совершить термодинамический процесс, которому на фазовой диаграмме соответствует кривая, обходящая критическую точку К справа при
и соединяющая области газа и жидкости, то в этом случае газ непрерывным образом переходит в жидкость или наоборот без каких-либо скачков физических характеристик. Д.И.Менделеев определял критическую температуру как температуру абсолютного кипения жидкости без подвода какого-либо тепла извне.
Слайд 36В критическом состоянии наблюдаются очень большие флуктуации плотности вещества, которые
вызывают интенсивное рассеяние проходящего света и делают среду непрозрачной. Кроме
того, в критической точке очень медленно устанавливается термодинамическое равновесие.
В случае воды характеристики критической точки имеют следующие значения:
,
,
. Вода в таком состоянии обнаружена в земной коре на глубине несколько километров.
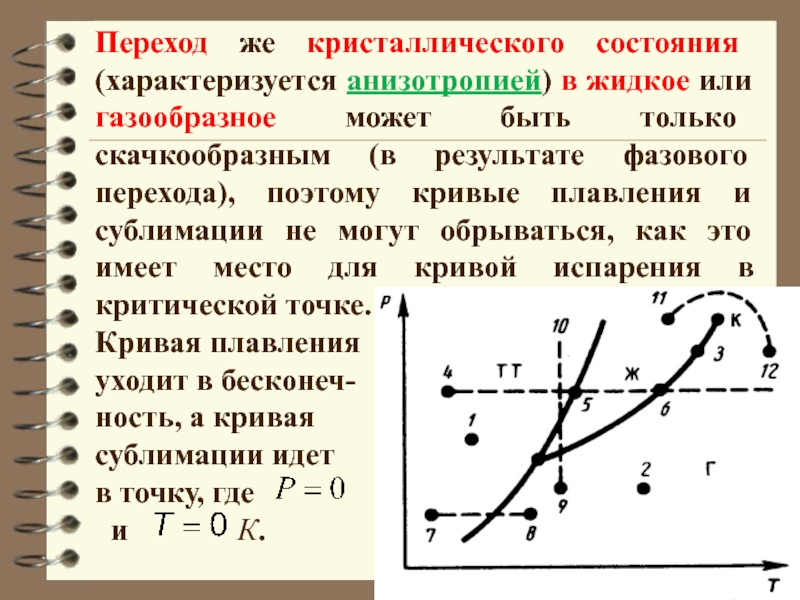
Слайд 37Переход же кристаллического состояния (характеризуется анизотропией) в жидкое или газообразное
может быть только скачкообразным (в результате фазового перехода), поэтому кривые
плавления и сублимации не могут обрываться, как это имеет место для кривой испарения в критической точке.
Кривая плавления
уходит в бесконеч-
ность, а кривая
сублимации идет
в точку, где
и К.