Слайд 1Термодинамика и статистическая физика
Слайд 2 Лекция № 2
Первое начало термодинамики
1. Внутренняя энергия.
Макроскопическая
работа. Количество теплоты.
2. Первое начало термодинамики.
3. Теплоёмкость.
Молярная теплоёмкость
идеального одноатомного газа при посто-
янном объёме и постоянном давлении.
4. Адиабатический процесс. Уравнение
адиабаты идеального газа.
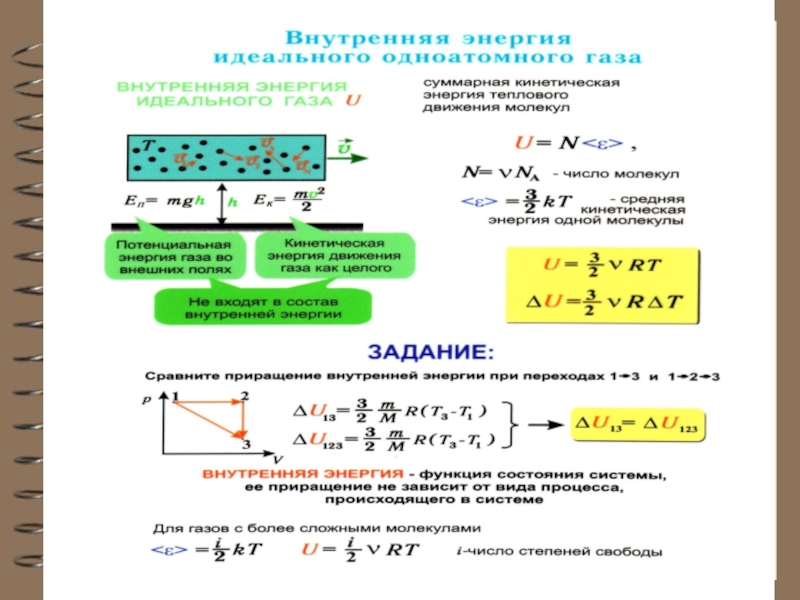
Слайд 3 Внутренняя энергия
Наряду с механической энергией любое тело (или система) обладает внутренней
энергией. Внутренняя энергия – энергия покоя (без движения сосуда).
Она складывается из:
- теплового хаотического движения молекул,
- потенциальной энергии их взаимодей-
ствия (для реального газа),
- кинетической и потенциальной энергии электронов в атомах, нуклонов в ядрах и так далее.
Слайд 4 В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой
энергии недостаточно, чтобы изменить строение атома, а тем более ядра).
Следовательно, фактически под внутренней энергией в термодинамике подразумевают энергию теплового хаотического движения молекул.
В термодинамике важно знать не абсолютное значение внутренней энергии,
а её изменение.
Слайд 5
Внутренняя энергия U одного моля идеального одноатомного газа
равна:
или
Таким образом, внутренняя энергия зави-сит только от температуры.
Внутренняя энергия U является функ-цией состояния системы и
не зависит от предыстории:
Слайд 6 В каждом состоянии система обладает определенным и
только таким значением внутренней энергии, поэтому можно записать
Так как U
– функция состояния, то
Этот справедливо для любой функции состояния.
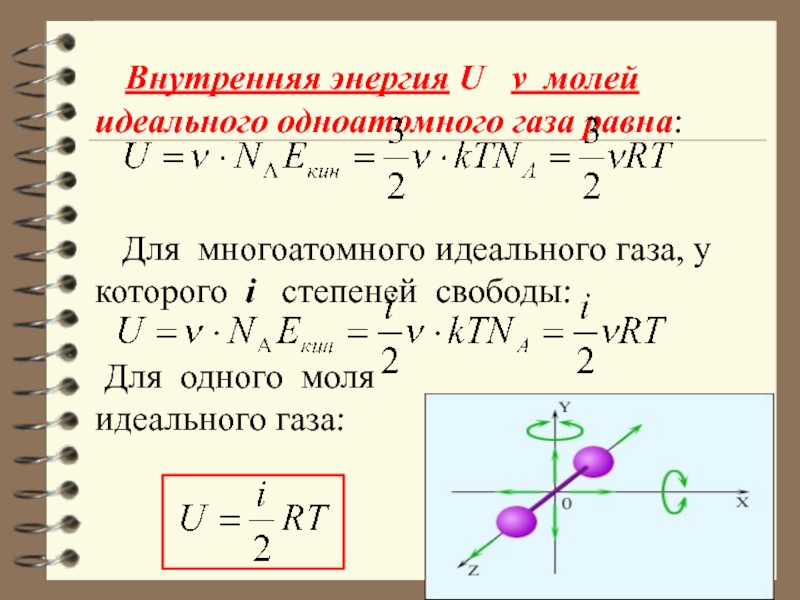
Слайд 7 Внутренняя энергия U ν молей идеального одноатомного
газа равна:
Для многоатомного идеального газа, у которого i степеней свободы:
Для одного моля
идеального газа:
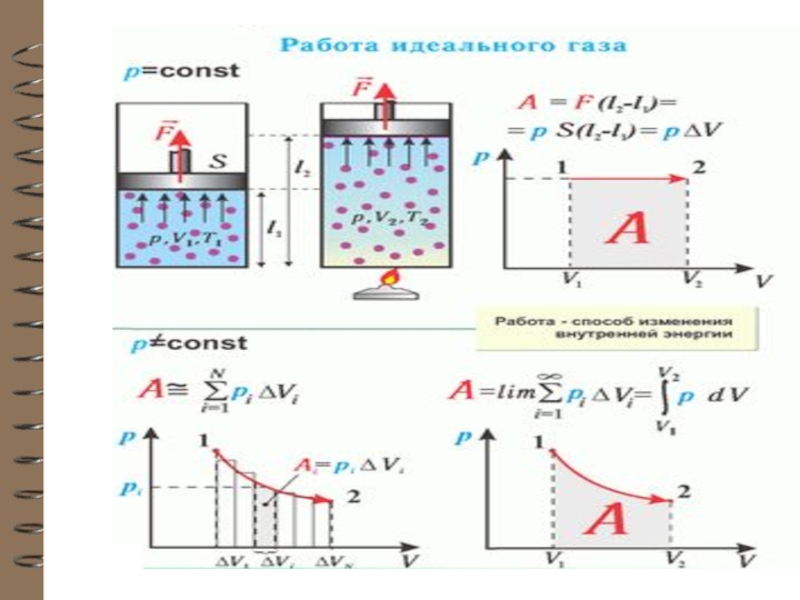
Слайд 10 Работа и теплота
Термодинамическая
система может обладать как внутренней, так и механичес-кой энергией и
разные системы могут обмениваться этими видами энергии.
Обмен механической энергией характеризуется совершённой работой А, а обмен внутренней энергией – количеством переданного тепла Q.
Механическая энергия может перехо-дить в тепловую энергию и обратно.
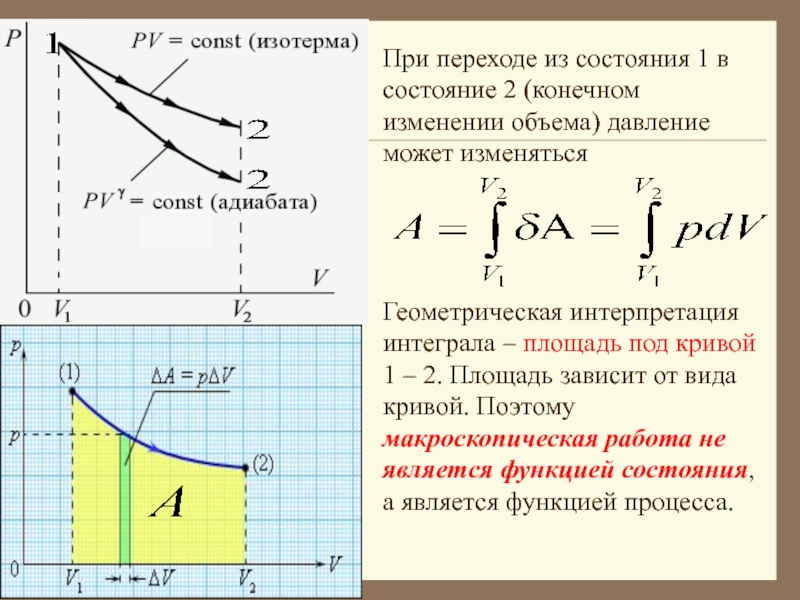
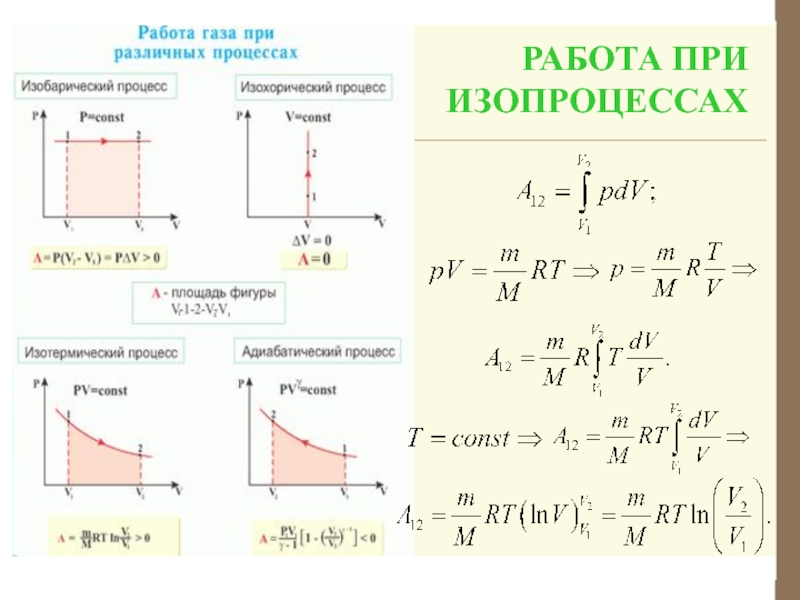
Слайд 13При переходе из состояния 1 в состояние 2 (конечном изменении
объема) давление может изменяться
Геометрическая интерпретация интеграла – площадь под
кривой 1 – 2. Площадь зависит от вида кривой. Поэтому макроскопическая работа не является функцией состояния, а является функцией процесса.
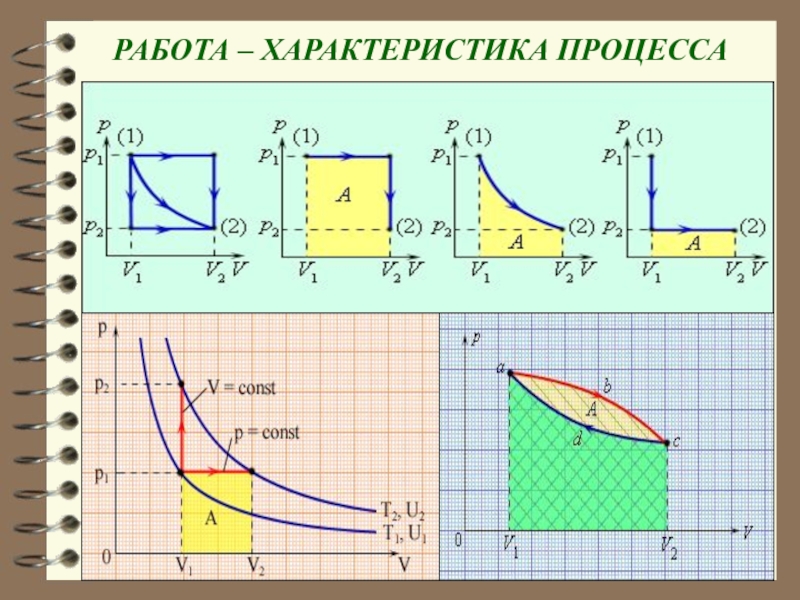
Слайд 15 РАБОТА – ХАРАКТЕРИСТИКА ПРОЦЕССА
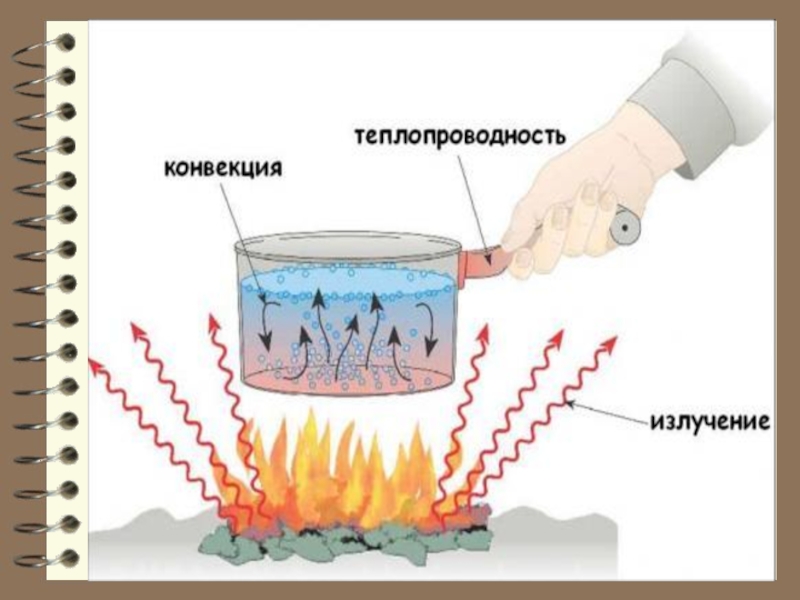
Слайд 16 Количество теплоты Q , представляет собой энергию, которая
передаётся от одного тела к другому при их контакте (непосредственно
или через 3-е тело) или
путём излучения.
Количество тепла (теплота) – мера изменения внутренней энергии системы в процессе теплопередачи: теплопроводность, тепловое излучение, конвекция (перенос теплоты, обусловленный различием температур в разных местах жидкости или газа).
Слайд 18 Первое начало термодинамики
(закон сохранения энергии при тепловых
процессах)
Количество теплоты, сообщаемой телу, идёт на увеличение внутренней энергии и
на совершение телом работы:
– это и есть первое начало термодинамики или закон сохранения энергии в термодинамике.
– изменение внутренней энергии тела равно разности сообщаемой телу теплоты и произведённой телом работы.
Слайд 19 Закон сохранения энергии для малого изменения состояния системы будет иметь
вид:
U – функция состояния системы;
dU – её полный дифференциал, а
δQ и δА таковыми не являются и их
приращения не являются полными
дифференциалами.
Слайд 20 Теплота Q и работа А зависят от того, каким образом
совершен переход из состояния 1 в состояние 2 (изохорически, адиабатически),
а внутренняя энергия U не зависит.
При этом нельзя сказать, что система, обладает определенным для данного состояния значением теплоты и работы.
Количество теплоты Q выражается в тех же единицах, что работа и энергия, т.е. в джоулях [Q] = Дж.
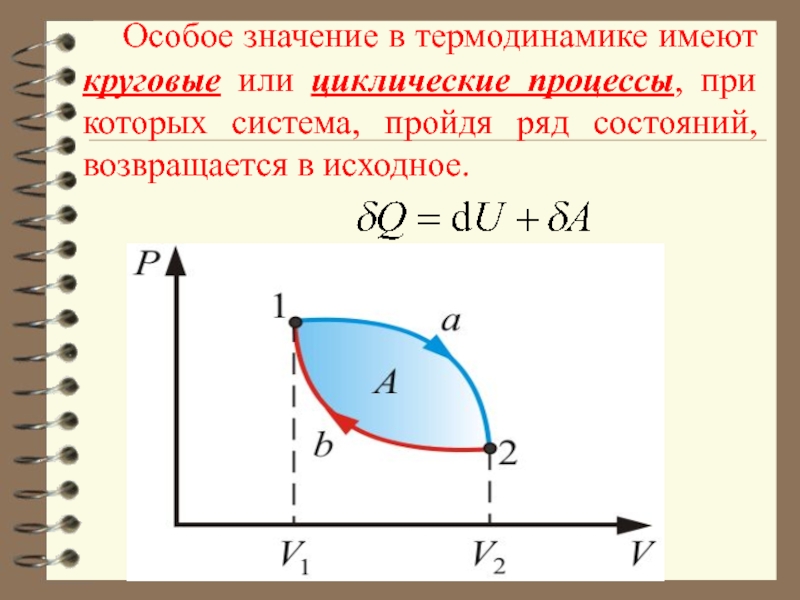
Слайд 21 Особое значение в термодинамике имеют круговые или циклические процессы, при
которых система, пройдя ряд состояний, возвращается в исходное.
то согласно первому началу термодинамики
т.е.
нельзя построить периодически действующий двигатель, который совершал бы бóльшую работу, чем количество сообщенной ему извне энергии. Иными словами, вечный двигатель первого рода невозможен.
Это одна из формулировок первого начала термодинамики.
Слайд 23 Теплоёмкость идеального газа
Теплоёмкость тела характеризуется
количеством теплоты, необходимой для нагревания этого тела на один градус
Размерность теплоемкости: [C] = Дж/К.
Теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.
Слайд 24 Удельная теплоёмкость Суд – есть количество теплоты, необходимое для
нагревания единицы массы вещества на
1 градус
[Cуд] = Дж/(кг∙К).
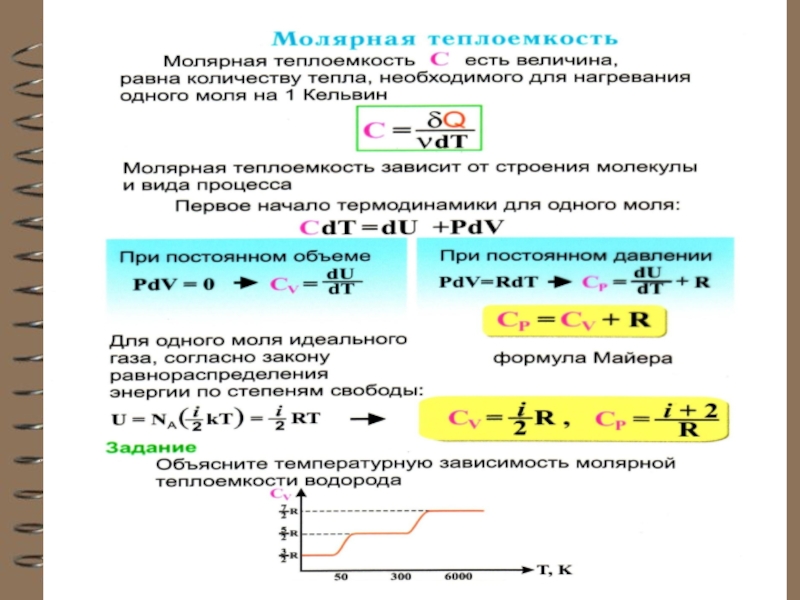
Для газов удобно пользоваться молярной теплоемкостью Сμ количество теплоты, необходимое для нагревания
1 моля газа на 1 градус
[Cμ] = Дж/(мольК).
Слайд 25 Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы
при нагревании.
Если газ нагревать при постоянном объёме, то всё подводимое
тепло идёт на нагревание
газа, то есть изменение его
внутренней энергии.
Теплоёмкость при
постоянном объёме СV
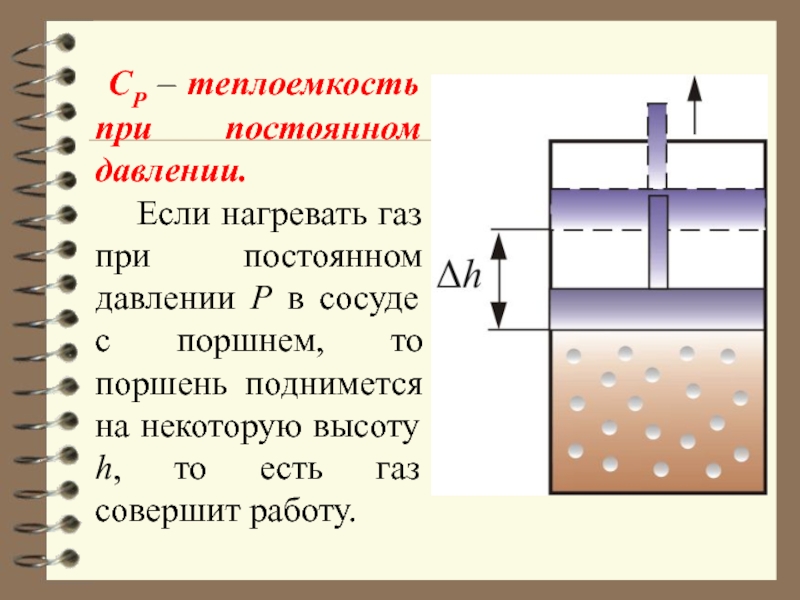
Слайд 26 СР – теплоемкость при постоянном давлении.
Если нагревать
газ при постоянном давлении Р в сосуде с поршнем, то
поршень поднимется на некоторую высоту h, то есть газ совершит работу.
Слайд 27 Следовательно, проводимое тепло затрачивается и на нагревание и на совершение
работы. Отсюда ясно, что
Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляет-ся передача тепла.
Следовательно Q и С не являются функциями состояния. Величины СР и СV оказываются связанными простыми соотношениями. Найдём их.
Слайд 28
При изобарическом процессе кроме увеличения внутренней энергии
происходит совершение работы газом (из I начала ТД):
Из основного уравнения молекулярно-кинетической теории для 1моля:
При изобарическом процессе Р = const.
Тогда получим:
Слайд 29Это уравнение Роберта Майера для одного моля газа. Из него
следует, что физический смысл универсальной газовой постоянной в том, что
R – численно равна работе, совершаемой одним молем газа при нагревании на один градус при изобаричес-ком процессе.
Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.
Для ν молей:
Слайд 30 В общем случае
так как внутреняя энергия U
может зависеть не только от температуры.
В случае 1 моля идеального газа спра-ведлива формула изм. внутренней энергии:
Из этого следует, что для 1 моля:
Слайд 31 Внутренняя энергия идеального газа является только функцией температуры (и не
зависит от V, Р и тому подобным), поэтому формула
справедлива для любого процесса ( для 1 моля).
Для произвольной массы идеального газа:
Слайд 32 Внутренняя энергия одного моля идеального одноатомного газа равна:
теплоемкость при постоянном объеме СV – величина постоянная, от темпера-туры не зависит.
Слайд 33 Внутренняя энергия одного моля идеального газа c i степенями свободы
равна:
теплоемкость при постоянном объеме СV – величина постоянная, от темпера-туры не зависит.
Слайд 34 Учитывая физический смысл R для изобарических процессов
можно записать:
(для одного моля). Отсюда для одноатомного:
Тогда,
теплоемкость при постоянном давлении для одноатомных газов:
Слайд 35
Для одного моля одноатомного
идеального газа:
Постоянная адиабаты (коэффициент Пуассона) для идеального
газа:
Для одноатомного идеаль-
ного газа (i = 3):
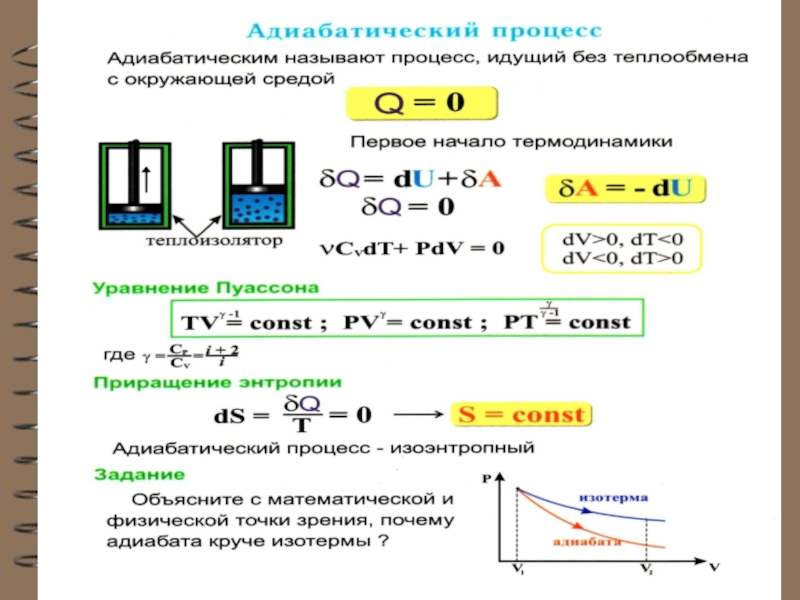
Слайд 37 Адиабатный (адиабатический) процесс
Это процесс, происходящий без теплообмена с окружающей
средой, т.е.
При адиабатном процессе работа
системы (или над системой) совершается за счет изме-нения внутренней энергии газа:
(из I начала ТД: при ).
Вывод уравнения адиабаты.
и A = PdV :
Для 1 моля идеального газа:
Слайд 38 Подставляя dT в уравнение:
Группируя PdV:
Делим на
где
Т.к. γ = const ( для одноатомного газа γ = 5/3 ), то
Слайд 39уравнение Пуассона или уравнение адиабаты для идеального газа
Или в переменных Т и V уравнение адиабаты
для идеального газа:
Слайд 41 Здесь уместно рассмотреть еще и политропный процесс – такой процесс,
при котором изменяются все основные параметры системы, кроме теплоемкости, т.е.
С = const.
Уравнение политропы
или
Здесь n – показатель
политропы:
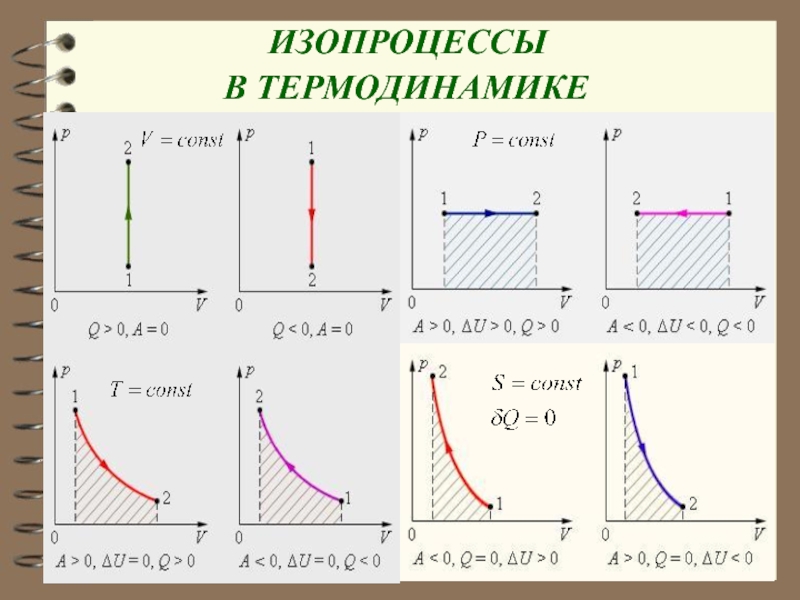
Слайд 42 С помощью показателя n можно легко описать любой
изопроцесс:
1. Изобарный процесс Р = const, n = 0
2. Изотермический процесс Т = const, n = 1,
3. Изохорный процесс V = const,
Слайд 434. Адиабатический процесс Q = 0,
n
= γ, Сад = 0.
Во всех этих процессах работу можно
вычислить по одной формуле: