Слайд 1Термодинамика и статистическая физика
Слайд 2 Лекция № 12
Элементы физической кине-тики. Процессы переноса.
1. Процессы релаксации в газах. Роль стол-кновения частиц. Эффективное сечение.
Средняя длина свободного пробега.
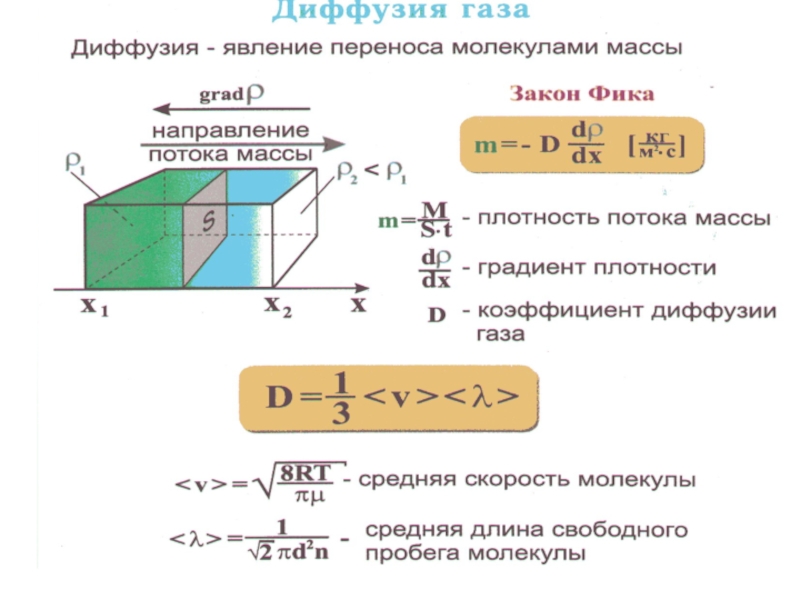
2. Диффузия. Закон Фика. Коэффициент диффузии.
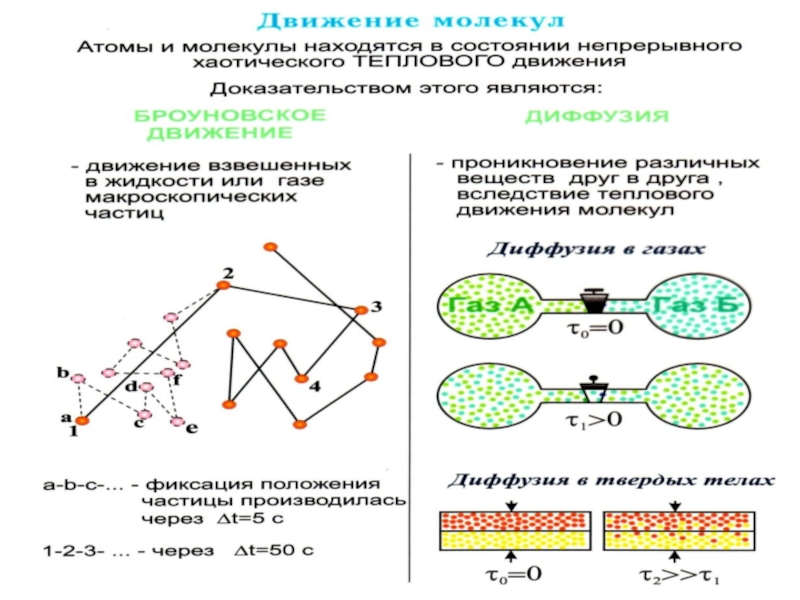
3. Броуновское движение.
Слайд 3 Далеко не всегда система находится в сос-тоянии термодинамического равновесия.
Если температура системы в разных точка неодинакова, то нельзя приписать
системе определённое значение температуры. В этом случае состояние называется неравновес-ным. Процесс перехода системы из нерав-новесного состояния в равновесное назы-вается процессом релаксации. За время релаксации принимают время, за которое первоначальное отклонение какой-либо величины от равновесного значения уменьшается в е раз.
Слайд 4 Явления переноса в газах
Молекулы в газе движутся со скоростью звука, с такой же
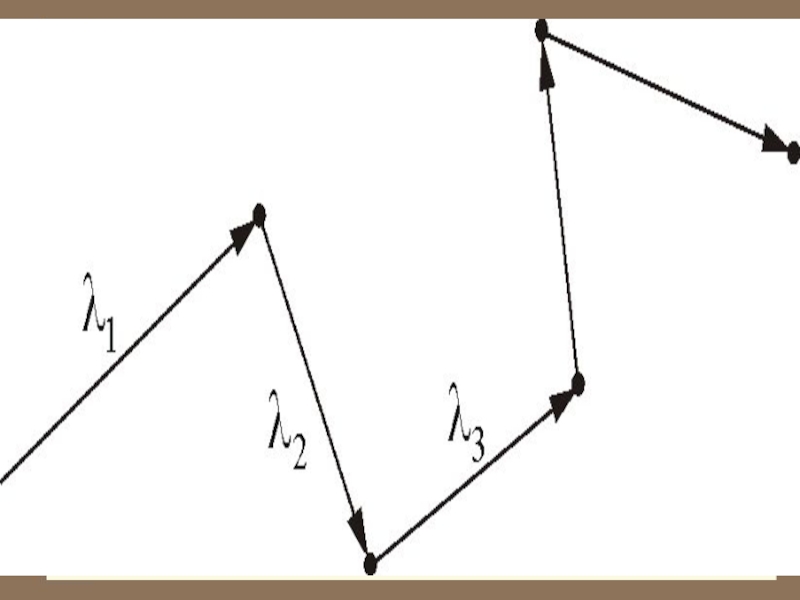
скоростью движется пуля. Однако, находясь в противоположном конце комнаты, запах разлитой пахучей жидкости мы почувствуем через сравнительно большой промежуток времени. Это происходит потому, что молекулы движутся хаотически, сталкиваются друг с другом, траектория движения у них ломанная.
Слайд 6 Число столкновений и средняя длина свободного пробега молекул в
газах
Обозначим – длина свободного пробега молекулы.
Медленность явлений переноса, например диффузии ароматических веществ – «распространение запаха», при относительно высокой скорости теплового движения молекул
( ) объясняется столкновениями молекул.
Слайд 7 Расстояние, проходимое молекулой в среднем без столкнове-ний, называется средней длиной
свободного пробега:
– средняя скорость теплового движения,
– среднее время между двумя столкновениями.
средняя длина свободного пробега.
Слайд 8 Модель идеального газа – твёрдые шарики одного диаметра, взаимодействующие между
собой только при столкновении.
Обозначим σ – эффективное сечение молекулы –
полное поперечное сечение рассеяния, характеризующее столкновение между двумя молекулами .
Слайд 9– эффективное
сечение молекулы
– площадь в которую
не может
проникнуть центр любой другой молекулы.
d
d
Слайд 10 За одну секунду молекула проходит путь, равный средней арифметической скорости
За ту
же секунду молекула претерпевает ν столкновений.
Слайд 11Подсчитаем число столкновений ν.
Вероятность столкновения
трех и более молекул бесконечно мала.
Предположим, что все молекулы застыли,
кроме одной. Её траектория будет представлять собой ломаную линию. Столкновения будут только с теми молекулами, центры которых лежат внутри цилиндра радиусом d.
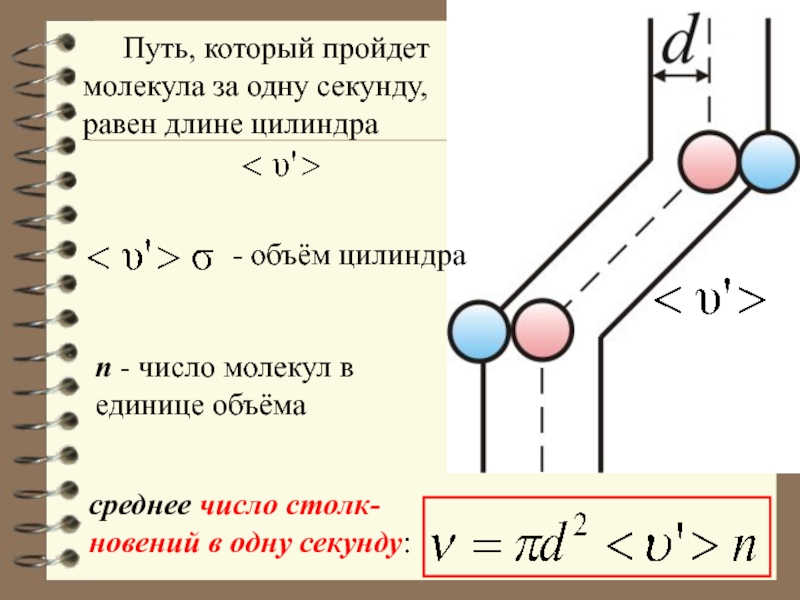
Слайд 12 Путь, который пройдет молекула за одну секунду, равен длине цилиндра
- объём цилиндра
n - число молекул в единице объёма
среднее число
столк-новений в одну секунду:
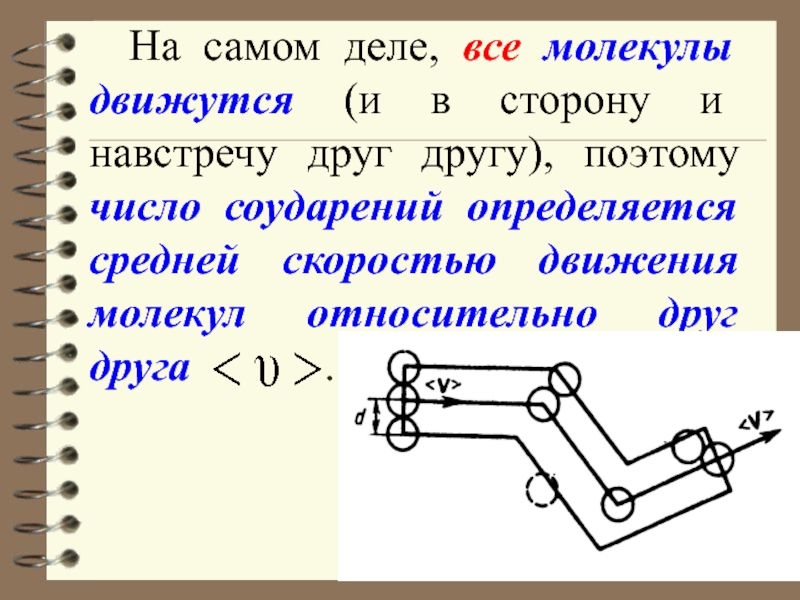
Слайд 13 На самом деле, все молекулы движутся (и в сторону и
навстречу друг другу), поэтому число соударений определяется средней скоростью движения
молекул относительно друг друга .
Слайд 14 По закону сложения случайных величин:
Так как
- средняя длина
свободного пробега
Тогда:
Слайд 15 Из уравнения состояния идеального газа выразим
n через давление P и температуру Т
Так как ,
то есть тогда
Слайд 16 Таким образом, при заданной температуре, средняя длина свободного
пробега обратно пропорциональна давлению Р:
Например: d
= 3 Å = 31010 м,
Р = 1 атм., Т = 300 К,
а, т.к.
Число столкновений:
Диффузия от латинского diffusio – распространение, растекание
взаимное проникновение соприкасающихся веществ друг в друга, вследствие теплового движения частиц вещества.
Диффузия происходит в направлении уменьшения концентрации вещества и ведет к его равномерному распределению по занимаемому объему.
Слайд 19 Диффузия имеет место в газах, жидкостях и
твердых телах.
Наиболее быстро диффузия происходит в газах, медленнее в
жидкостях, еще медленнее в твердых телах, что обусловлено характером движения частиц в этих средах.
Для газа диффузия – это распределение молекул примеси
от источника (или взаимная диффузия газа).
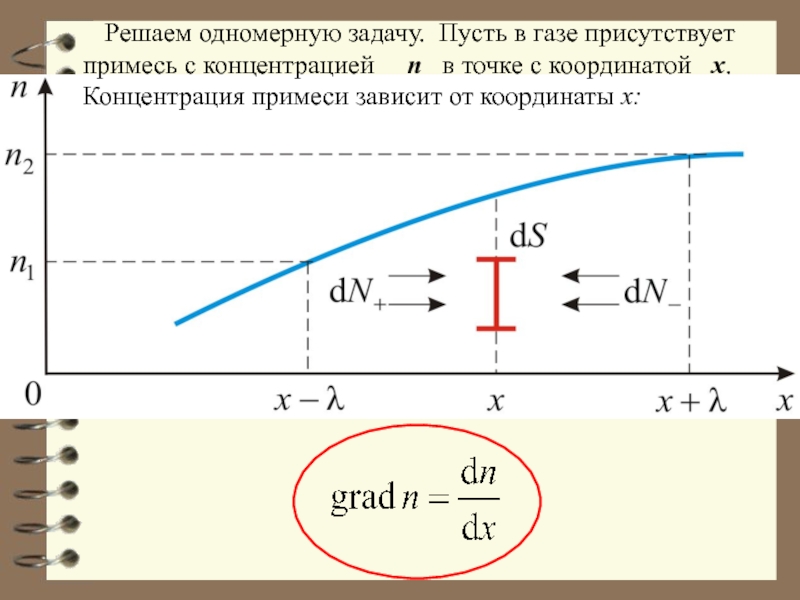
Слайд 20 Решаем одномерную задачу. Пусть в газе присутствует примесь
с концентрацией n в точке с координатой
х. Концентрация примеси зависит от координаты х:
Слайд 21 Градиент концентрации, в общем случае равен:
Так как у нас одномер-
ная задача, то:
При наличии grad n, хаотическое движение будет более направленным и возникнет поток молекул примеси, направленный от мест с большей концентрацией к местам с меньшей концентрацией. Найдём этот поток.
Слайд 22где n1 концентрация молекул слева от площадки dS,
а
n2 концентрация справа.
Подсчитаем число молекул,
проходящих через единичную площадку dS в направлении слева на право и справа налево , за время dt.
Слайд 23 Результирующий диффузионный поток через единицу площади в единицу времени:
но
тогда
– коэффици-
ент диффузии.
Тогда диффузионный поток будет равен:
или в общем случае (в трёхмерной системе):
- закон Фика
Слайд 25 Из закона Фика видно, что диффузионный поток, направлен в сторону
уменьшения концентрации.
При этом коэффициент диффузии D численно равен диффузионному
потоку через единицу площади в единицу времени при
Измеряется коэффициент диффузии D в м/с2.
Слайд 29 Броуновское движение
Броуновское движение
в жидкости тем оживлённее, чем меньше вязкость жидко-сти. Его едва
удаётся подметить в глицери-не, а в газах, оно чрезвычайно интенсивно. Броуновское движение вызывается толчка-ми, испытываемыми взвешенными части-цами со стороны окружающих молекул, совершающих тепловое движение. Под вли-янием ударов молекул окружающей среды скорость броуновской частицы меняется.
Слайд 30 Пусть броуновская частица имеет форму шарика радиуса r
. Если небольшой шарик равномерно движется в жидкости со скоро-стью
υ , то, как показывает опыт и теория, на него действует сила сопротивления F, пропорциональная скорости υ. Коэффици-ент пропорциональности в формуле
называется подвижностью частицы – В.
Подвижность частицы B связана с коэф-фициентом диффузии соотношеним Эйн-штейна: