Слайд 1Термодинамика и статистическая физика
Слайд 2 Лекция № 4
Статистический метод описания.
1. Основная задача статистической
физики. Микросостояние системы частиц.
2. Элементарные сведения из теории вероятностей.
3.Функция распределения. Среднее значение.Дисперсия
Закон распределения Максвелла.
1. Пространство скоростей. Принцип детального равновесия.
2. Распределение молекул газа по скоростям
в условиях термодинамического равновесия.
3. Закон распределения скоростей Максвелла. Характерные скорости молекул.
Слайд 3 Состояние системы детально охарактери-зованное на уровне каждой частицы называется
микросостоянием.
Микросостояния системы описываются
заданием в каждый момент времени коорди-нат
и скоростей всех молекул, атомов, а так-же электронов, атомных ядер и прочих час-тиц, из которых построены тела системы.
Состояние системы описанное с помощью макроскопических параметров, характеризу-
ющих систему в целом (P ,V ,T, n, m) называется макросостоянием.
Слайд 4Детальное описание состояний макроскопи-ческих систем, ввиду колоссальности числа частиц в
них, не только невозможно осуще-ствить фактически, но оно не представляет
никакого интереса. В термодинамике имеют смысл средние значения, которые прини-мают при определённых условиях какие-то функции микросостояния системы. Про величины такого рода говорят, что они име-ют статистический характер или являются статистическими. Например, давление, плотность, температура, средний квадрат смещения частицы.
Слайд 5Основная задача статистической физики: найти наиболее вероятные распределения молекул по
скоростям, энергиям, импульсам и т.д. И средние значения соответствующих параметров.
Слайд 6 Элементарные сведения из теории
вероятностей.
С точки зрения атомно-молекулярного строения
вещества величины, встречающиеся в макроскопической физике, имеют смысл средних значений, которые принимают некоторые функции от микроскопических переменных системы. Величины такого рода называются статистическими. Примерами таких величин являются давление, температура, плотность и др.
Слайд 7 Статистические закономерности изучаются теорией вероятностей.
Событиями или
случаями в теории вероятностей называют всякие явления, относительно которых имеет
смысл ставить вопрос, могут они происходить или нет. Опыт в теории вероятностей называется испытанием.
Если при данных условиях событие обязательно произойдёт, то оно назы-вается достоверным событием.
Слайд 8 Если событие произойти не может, то его называют невозможным.
Событие называют случайным, если в результате испытания оно может
как произойти, так и не произойти. Например, при игре в орлянку, может выпасть либо орёл, либо решка. Это- случайное событие. Но бросая много раз монету приблизительно в половине случаев будет герб. В этом случае вероятность выпадения герба равна ½.
Слайд 9 Математическое определение вероятности: вероятность какого-либо события – это
предел, к которому стремится отношение числа случаев, приводящих к осуществлению
события,
к общему числу случаев, при бесконечном увеличении последних:
Здесь n число раз, когда событие произошло, а n общее число опытов. Отсюда следует, что Р может принимать значения от нуля до единицы.
Слайд 10 По определению Лапласа, вероятность - отношение числа благоприятных случаев
к числу возможных случаев.
Если событие достоверно, то P =
1. Если со-бытие не может произойти вообще, то P = 0.
Слайд 11 События несовместимы, если появление одного из них исключает
появление любого из остальных.
Теорема сложения вероятностей.
Вероятность
суммы несовместных собы-тий равна сумме вероятностей этих событий
Событие, состоящее в появлении либо события А , либо события В. Например, в ящике красные, зелёные и белые шары. Вероятность вынуть цветной шар:
Слайд 12 Сумма вероятностей всех единственно возможных и несовместимых событий равна
единице:
- это утверж-
дение является следствием теоремы сложе-ния вероятностей. Т.к. события единствен-но возможны, то появление одного из них (безразлично какого) есть событие досто-верное. Вероятность такого события равна единице. Но по теореме о сложении вероят-ностей вероятность этого события может быть представлена суммой
Слайд 13 Это соотношение часто называют условием нормировки вероятностей.
Теорема
умножения вероятностей.
Вероятность произведения двух событий А и В равна произведению
вероятности одного из них Р(А) на вероятность другого, вычисленную в предположении, что первое событие произошло Р(В/А) – это условная вероятность события В, при условии, что событие А произошло.
Слайд 14 Если события А и В независимы (их вероятности не
зависят от того, произош-ло второе событие или нет), то
вероятность произведения
2-х независи-мых событий равна произведению их вероятностей. Например, есть три шара: красный, зелёный и белый. Какова веро-ятность того, что при последовательном вынимании 2-х шаров они окажутся зе-лёным и красным? Если вынуть один шар, то вероятность, что он окажется
Слайд 15либо зелёным, либо красным (событие А), равна по теореме сложения
вероятностей:
Если событие А произошло, то осталось два шара один
из которых будет либо зе-лёный, либо красный. Вероятность вы-нуть такой шар (событие В) равна:
. Искомая вероятность по теореме умножения равна:
Слайд 16 Существует ещё одна интерпретация вероятности, применяющаяся в физике. Пусть
в закрытом сосуде имеется одна моле-кула. Сталкиваясь со стенками, молекула
беспорядочно отражается от них и побывает в различных местах сосуда. Если наблюдать за молекулой в течение длительного времени Т и при этом часть времени t она провела в объёме V. Отношение t / T называется от-носительным временем пребывания молеку-лы в объёме V. Предел этого отношения
- вероятность нахождения
молекулы в объёме V.
Слайд 17 Важным понятием в теории вероятностей и её приложениях является
понятие среднего значения. Пусть произведено N однотип-ных измерений одной и
той же величины x при неизменных условиях. Пусть в n1 случа-ях измеренное значение величины x оказа-лось равным x1 , в n2 случаях – x2,…, в nm случаях – xm , ( n1 + n2 + n3 + …+ nm = N ).
Среднее значение измеряемой величины определяется выражением:
Слайд 18 Отношение , т.е. отношение числа наб-людений
при которых величина x имеет значение
, к общему числу наблюдений N, есть вероятность появления при измерениях значений , т.е. ( подразумевается,
что - вероятность события) и
т.д. для упрощения вместо lim пишут
и получаем среднее значение:
Слайд 19 Введём понятие отклонения результатов отдельных измерений от среднего значения
< x > , т.е.
, где i = 1,2,…,N
Дисперсия есть среднее арифметическое квадратов отклонений наблюдаемых значений (x1, x2,...,xm) случайной величины
от их среднего значения:
Среднее квадратичное отклонение:
Слайд 20 Распространим полученные результаты на случай когда характеризующая систему
ве-личина x может принимать непрерывный ряд значений от
0 до ∞ . В этом случае го-ворят, что величина x имеет сплошной (или непрерывный) спектр значений (в предыду-щем случае спектр значений был дискретным).
Возьмём очень малую величину а ( скажем,
а = 10‾¹º ) и получим ∆no измерений, при которых 0< x < a , ∆n1, при которых а< x < 2a,
…, ∆nx , при которых результат измерений находится в интервале от x до x + а и т.д.
Слайд 21 Вероятность того, что результат измерений окажется в интервале
от нуля до а , равна:
,
в интервале от а до 2а: ,…,
в интервале от x до x + а :
.
Начертим ось x и отложим вверх от неё полоски шириной а и высотой .
Получим столбчатую диаграмму,
которая называется гистограмма.
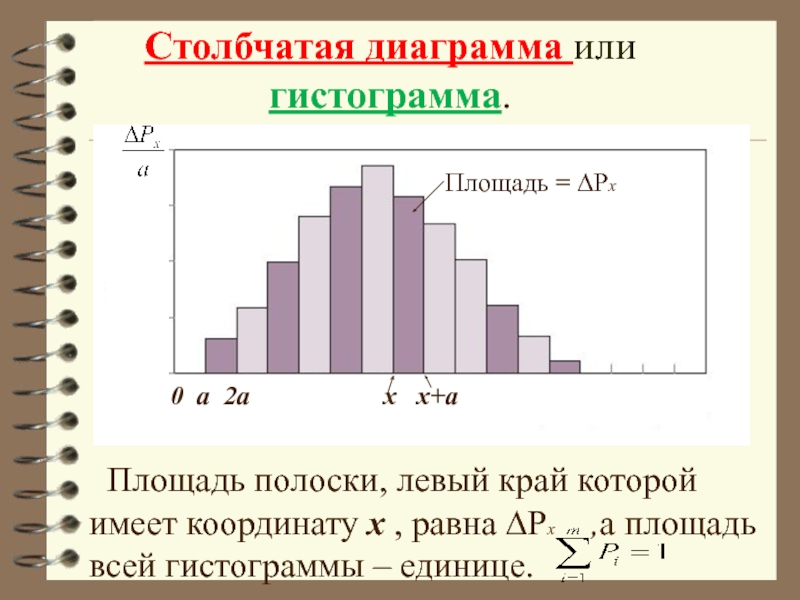
Слайд 22 Столбчатая диаграмма или
гистограмма.
Площадь полоски, левый край которой
имеет координату x , равна ∆Рx ,а площадь всей гистограммы – единице.
0 а 2а x x+a
Площадь = ∆Рx
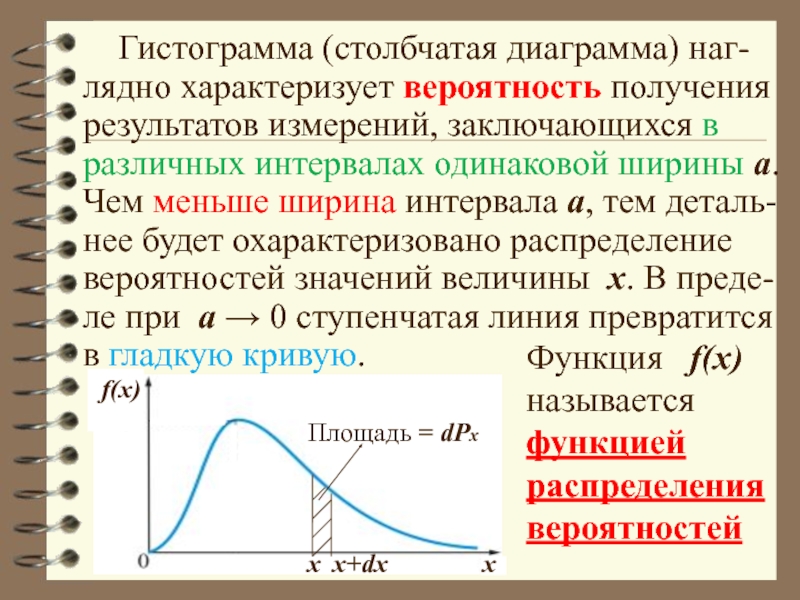
Слайд 23 Гистограмма (столбчатая диаграмма) наг-лядно характеризует вероятность получения результатов
измерений, заключающихся в различных интервалах одинаковой ширины а. Чем меньше
ширина интервала а, тем деталь-нее будет охарактеризовано распределение вероятностей значений величины x. В преде-ле при а → 0 ступенчатая линия превратится в гладкую кривую.
x
x
x+dx
Площадь = dРx
f(x)
Функция f(x) называется функцией
распределения
вероятностей
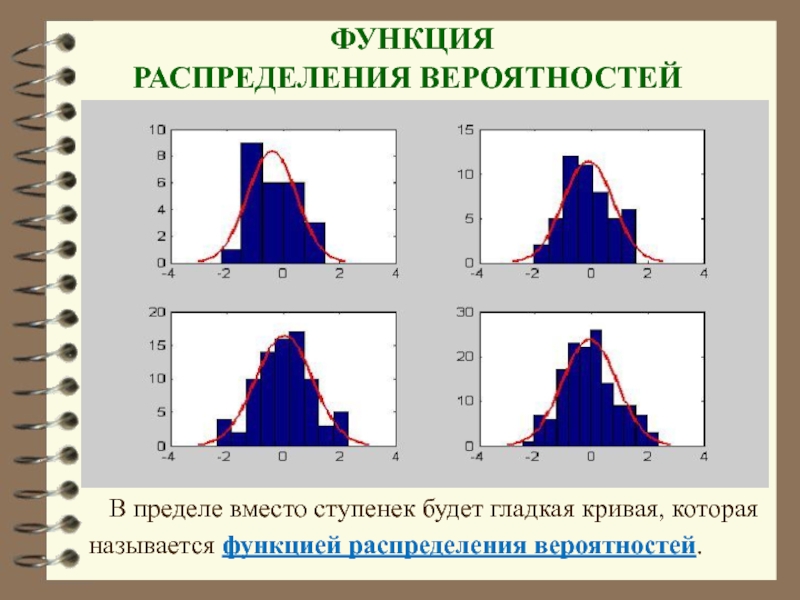
Слайд 24 ФУНКЦИЯ
РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
В пределе вместо ступенек будет гладкая
кривая, которая
называется функцией распределения вероятностей.
Слайд 25 Площадь столбика ширины dx равна ве-роятности того, что
результат измерения окажется в пределах от x до x+dx.
Обозна-чив эту вероятность через dPx , получим:
Индекс “x” при dP указывают на то, что имеется в виду вероятность для интервала, левый край которого лежит в точке с коорди-натой x . Площадь, ограниченная кривой распределения, так же как и площадь гисто-граммы, равна единице. Это означает:
- условие нормировки
dPx = f(x)∙dx
Слайд 26 Зная функцию распределения f(x) , можно найти среднее
значение результатов измере-ния величины x . В
случаях получается результат, равный x. Сумма таких результатов определяется выражением:
. Сумма всех возможных результатов равна:
Разделив это на число измерений N, полу-чим среднее значение величины x.
Слайд 27 Аналогичные рассуждения дают, что сред-нее значение некоторой функции φ(x)
можно вычислить по формуле:
Например:
Слайд 28 Закон распределения Гаусса.
Нормальное
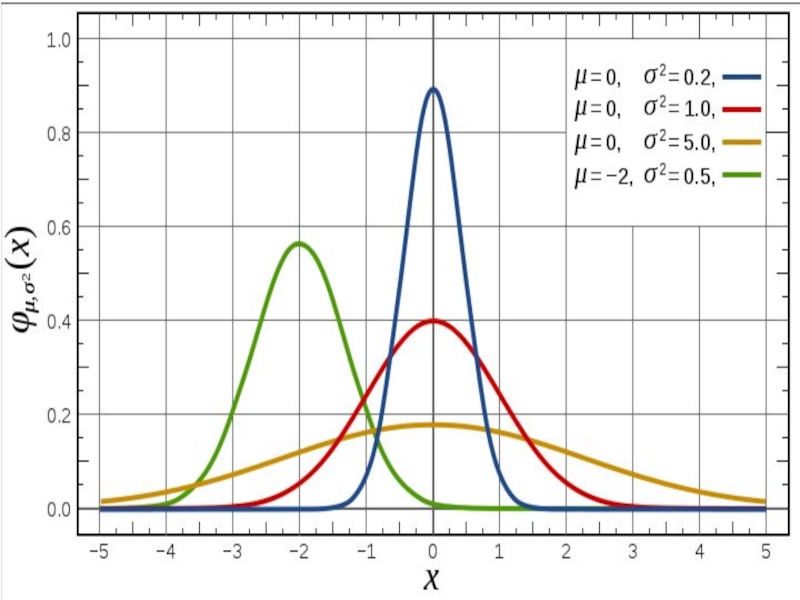
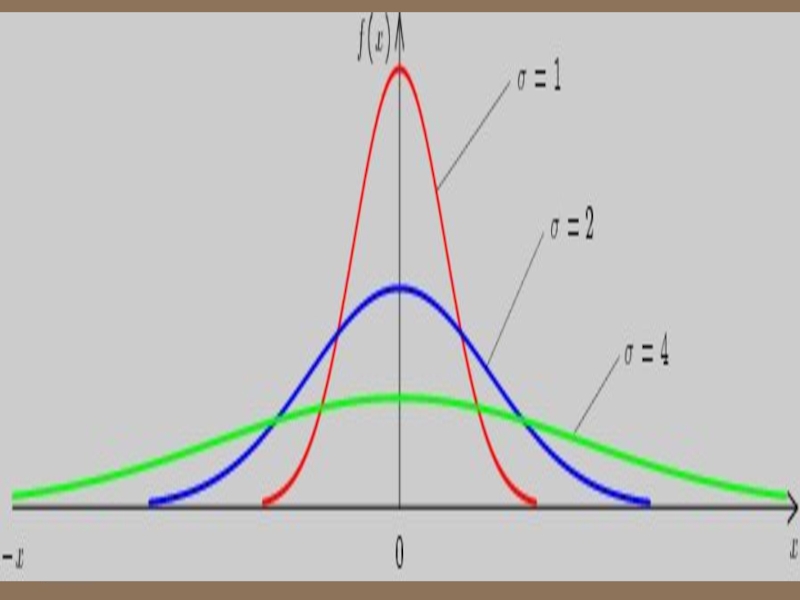
распределение, также называ-емое гауссовским распределением или распре-делением Гаусса — распределение
вероятнос-тей, которое задается функцией плотности распределения:
где параметр μ — среднее значение (математи-ческое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
Слайд 31Гаусс (Gauss) Карл Фридрих (30.4.1777, Брауншвейг, - 23.2.1855, Гёттинген), немецкий
математик, внёсший фундаментальный вклад также в астрономию и геодезию.
Слайд 33
Закон распределения скоростей молекул при тепловом
равновесии
Возьмём газ, состоящий из очень большого числа
N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при определённой температуре Т ( т.е. в условиях термодинамического равновесия ). Предполагается, что силовые поля, действующие на газ, отсутствуют.
В газе в состоянии хаотического движения должны компенсировать
Слайд 34друг друга всякие два противоположно направленные процесса. Скорости таких противоположно
направленных процессов должны быть одинаковыми. Это положение называется принципом детального
равновесия. Если бы оно не выполнялось, то тепловое движение молекул в какой-то мере устранило бы беспорядочный характер и приобрело бы черты, свойственные упорядоченному. Принцип детального равновесия справед-лив для любых систем в состоянии хаоса.
Слайд 35 Закон распределения скоростей
Максвелла.
Возьмём в воображаемом пространстве, которое назовём
υ – пространством (пространством скоростей), прямоуго-льные координатные оси, по которым будем откладывать значения отдельных молекул (имеются в виду компоненты скорости по осям x, y, z, взятым в обычном пространстве).
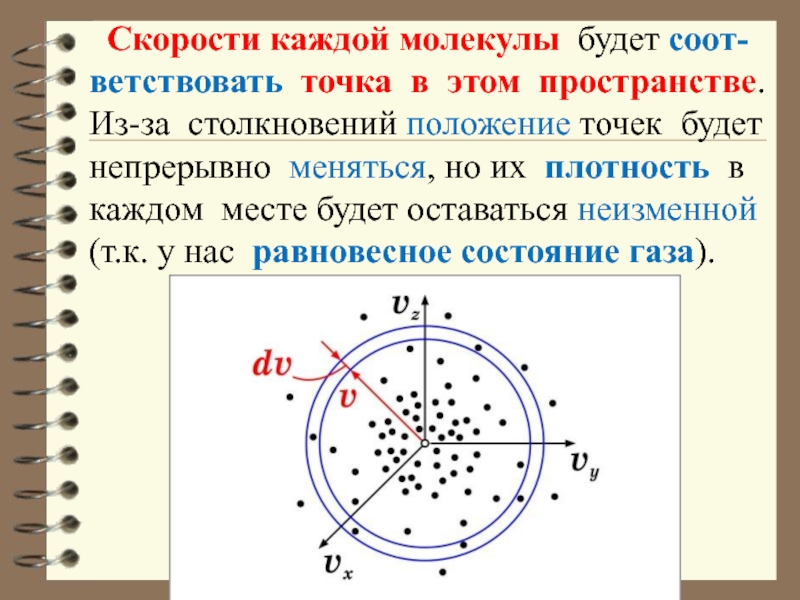
Слайд 36 Скорости каждой молекулы будет соот-ветствовать точка в этом пространстве.
Из-за столкновений положение точек будет непрерывно меняться, но их плотность
в каждом месте будет оставаться неизменной (т.к. у нас равновесное состояние газа).
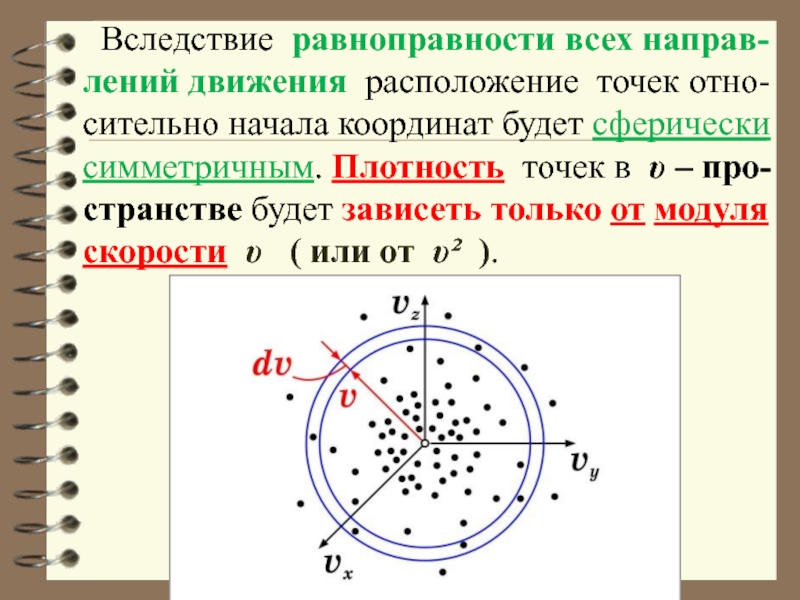
Слайд 37 Вследствие равноправности всех направ-лений движения расположение точек отно-сительно начала
координат будет сферически симметричным. Плотность точек в υ – про-странстве
будет зависеть только от модуля скорости υ ( или от υ² ).
Слайд 38 Молекулы движутся хаотически. Среди них есть и очень быстрые,
и очень медленные. Благодаря беспорядочному движению и случайному характеру их
взаимных столкновений, молекулы определённым образом распределяются по скоростям. Это распределение оказывается однозначным и единственно возможным, и не только не противоречит хаотическому движению, но именно им и обусловлено.
Слайд 39 Мы будем искать число частиц (n) скорости
которых лежат в определён-ном интервале значения скорости υ ( т.е.
от υ до ).
Здесь n – число благоприятных частиц, попавших в этот интервал.
Очевидно, что в единице объёма число таких благоприятных частиц тем больше, чем больше υ.
Слайд 40 Ясно так же, что n должно быть пропорционально концентрации молекул
n . Число n зависит и от самой скорости, так
как в одинаковых по величине интервалах, но при разных абсолютных значениях скорости, число молекул будет различным.
Смысл сказанного легко понять из простого примера: неодинаково, число людей в возрасте от 20 до 21 года и от 90 до 91 года.
И так:
Здесь f (υ) – функция распределения молекул по скоростям, n – концентрация молекул и υ - интервал значений скоростей.
В пределе, получим:
Физический смысл f(υ) в том, что это отношение числа молекул, скорости которых лежат в определенном интерва-ле скоростей, к общему числу молекул в единичном интервале
скоростей:
Слайд 42 Таким образом, f(υ) – имеет смысл
вероятности, то есть показывает, какова вероятность любой молекулы газа в
единице объёма иметь скорость, заключён-ную в единичном интервале, вклю-чающем заданную скорость υ.
В данном случае f(υ) называют плотностью вероятности.
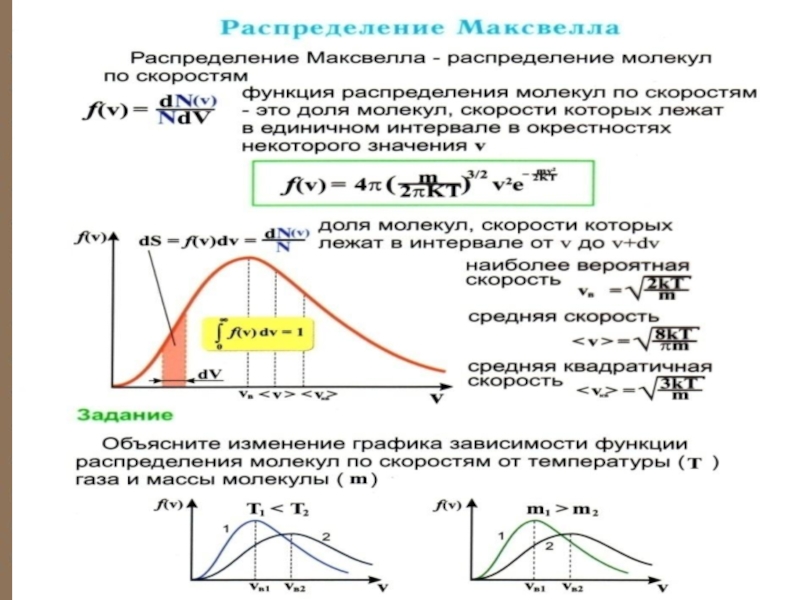
Слайд 43Функция распределения Максвелла
Пусть имеется n тождественных молекул, находящихся в
состоянии беспорядочного теплового движения при определенной температуре. После каждого акта
столкновения между молекулами, их скорости меняются случайным образом.
В результате невообразимо большого числа столкновений устанавливается стационарное равновесное состояние, когда число молекул в заданном интервале скоростей сохраняется постоянным.
Слайд 44 В результате каждого столкно-вения проекции скорости молекулы
испытывают случайное изменение на υx, υy, υz, причем изменения каждой
проекции скорости незави-симы друг от друга.
Найдем в этих условиях, каково число частиц dn из общего числа n имеет скорость в интервале
от до .
Слайд 45 При этом, мы не можем ничего определенного сказать о точном
значении скорости той или иной частицы υi, поскольку за столкновениями
и движениями каждой из молекул невозможно проследить ни в опыте, ни в теории. Такая детальная информация вряд ли имела бы практическую ценность.
Распределение молекул идеального газа по скоростям впервые было получено знаменитым английским ученым
Дж. Максвеллом в 1860 году с помощью методов теории вероятностей.
Максвелл Джеймс Клерк
(1831 – 1879) –
английский физик.
Работы посвящены
электродинамике,
молекулярной физике,
общей статике, оптике,
механике, теории упругос-
ти. Установил статистический закон,
описывающий распределение молекул
газа по скоростям.
Слайд 47 Скорость – векторная величина. Для проекции скорости на ось х
(x-ой составляющей скорости ), имеем:
или
где А1 из условия нормировки.
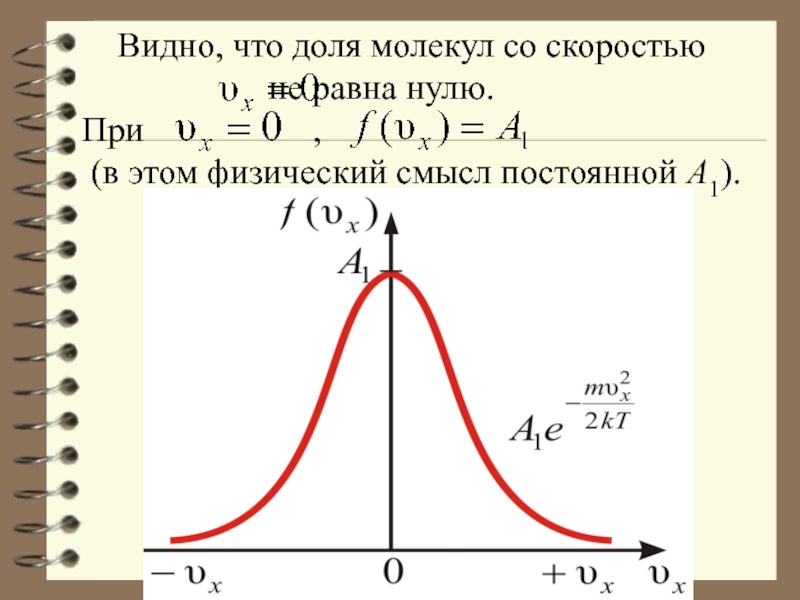
Слайд 48 Видно, что доля молекул со скоростью
не равна нулю.
При ,
(в этом физический смысл постоянной А1).
Слайд 49 Приведённое выражение и график справедливы для распределения молекул газа по
x-ым компонентам скорости. Очевидно, что и по y–ым и z–ым
компонентам скорости также можно получить:
Слайд 50 Вероятность того, что скорость молекулы одновременно удовлетворяет трём
условиям: x – компонента скорости лежит в интервале от υх
до ; y – компонента, в интервале от υy до ; z – компонента, в интервале от υz до будет равна произведению вероятностей каждого из условий в отдельности:
где ,
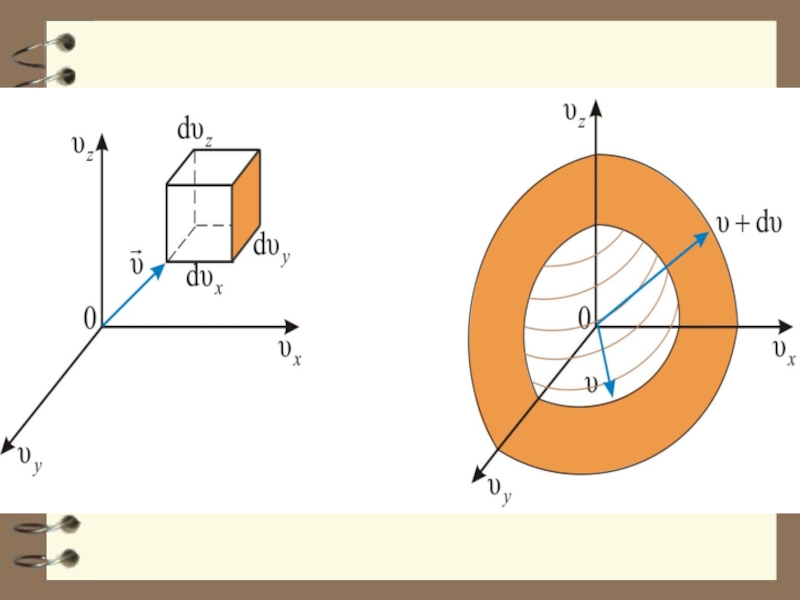
Этой формуле можно дать геометричес-кое истолкование: dnxyz – это число моле-кул в параллелепипеде со сторонами dυx, dυy, dυz, то есть в объёме , находящемся на
расстоянии от
начала координат
в пространстве
скоростей.
Слайд 52 Величина dnxyz не может зависеть от направления вектора
скорости. Поэтому надо получить функцию распределения молекул по скоростям независимо
от их направления, то есть по абсолютному значению скорости.
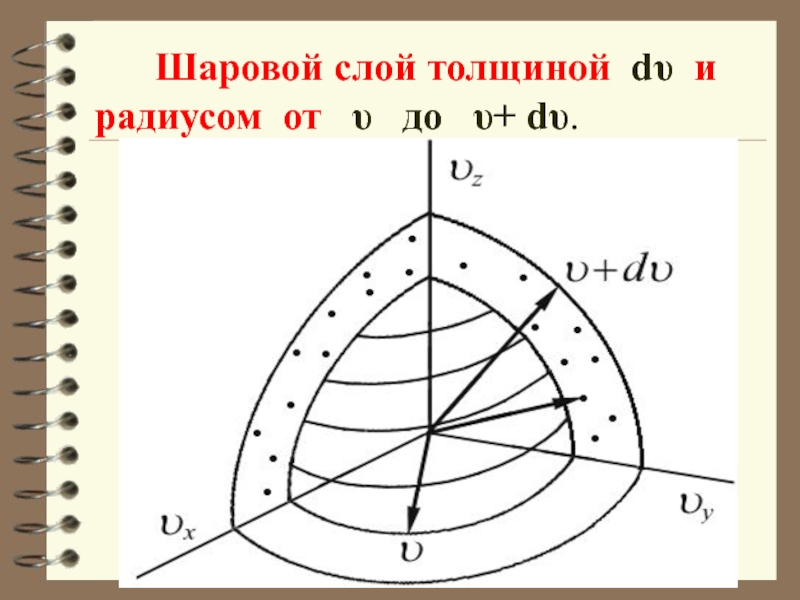
Если собрать вместе все молекулы в единице объёма, скорости которых заключены в интервале от υ до по всем направлениям, и выпустить их, то они окажутся через одну секунду в шаро-вом слое толщиной dυ и радиусом υ.
Слайд 53 Шаровой слой толщиной dυ и радиусом от
υ до υ+ dυ.
Слайд 55 Этот шаровой слой складывается из тех параллелепипедов, о которых говорилось
выше.
Объём этого шарового слоя:
Общее число молекул в слое:
Слайд 56 Отсюда следует закон Максвелла – распределение молекул по абсолютным значениям
скоростей:
где – доля всех частиц единичного объёма, скорости которых лежат в интервале от υ до
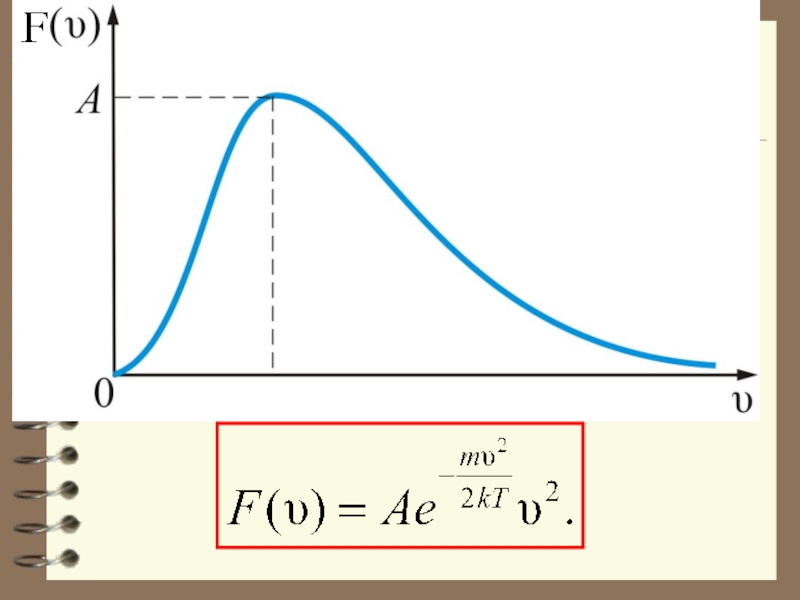
получаем плотность вероятности, или функцию Максвелла
распределения молекул по скоростям:
Эта функция обозначает долю молекул единичного объёма газа, абсолютные скорости которых заключены в единичном интервале скоростей, включающем данную скорость.
тогда получим:
График этой функции показан на рис.
Слайд 60Выводы:
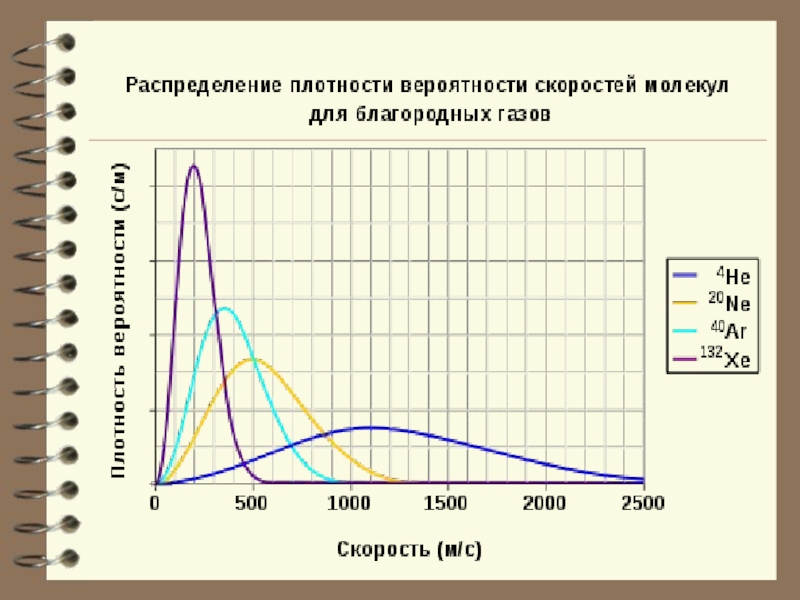
- Вид распределения молекул газа по скоростям, для каждого
газа зависит от рода газа (m) и от параметра состояния
(Т). Давление P и объём газа V на распределение молекул не влияют.
- В показателе степени стоит отношение, кинетической энергии, соответствующей данной скорости υ к средней энергии теплового движения молекул при данной температуре:
Слайд 61 Распределение Максвелла характеризует распределение молекул по значениям кинетической энергии (то
есть показывает, какова вероятность при данной температуре иметь именно такое
значение кинетической энергии).
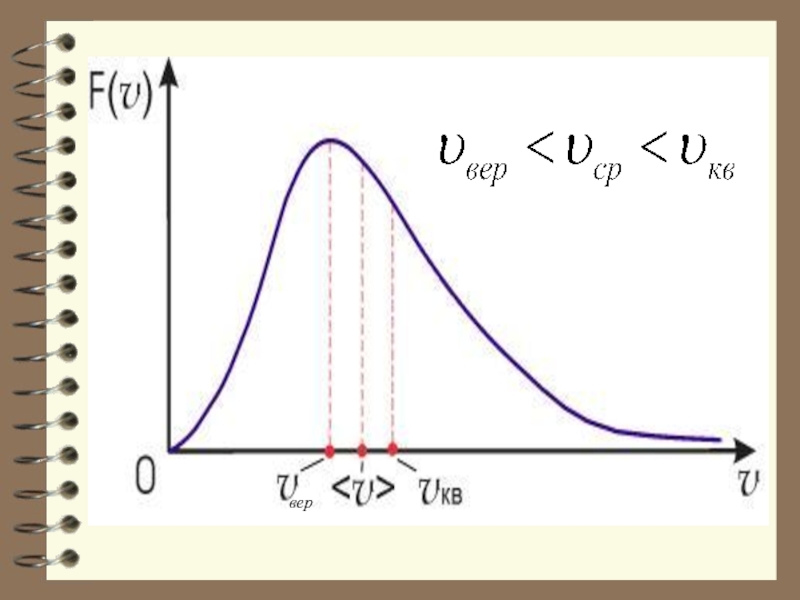
Слайд 62Характерные скорости (наиболее вероятная, среднеквадратичная и средняя скорости молекул газа).
Рассмотрим,
как изменяется с абсолютной величиной скорости число частиц, приходящихся на
единичный интервал скоростей, при единичной концентрации частиц.
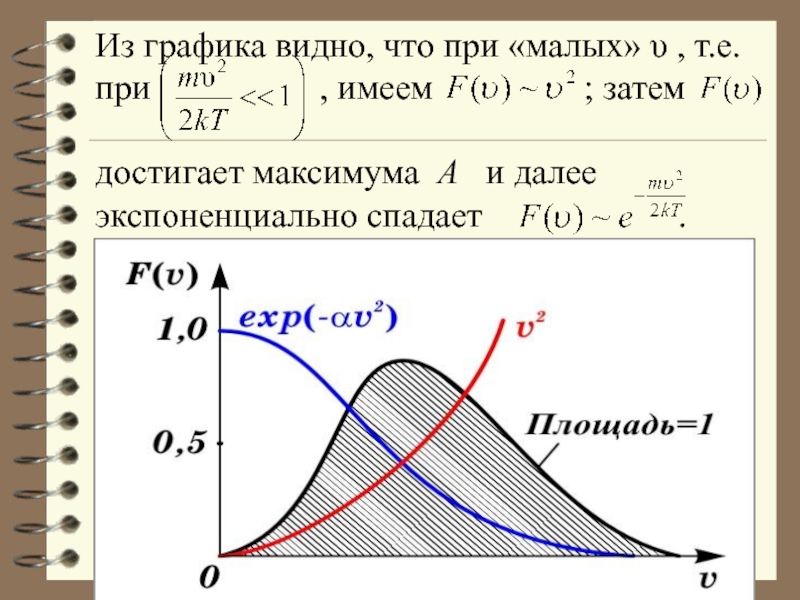
Слайд 63Из графика видно, что при «малых» υ , т.е. при
,
имеем ; затем
достигает максимума А и далее экспоненциально спадает .
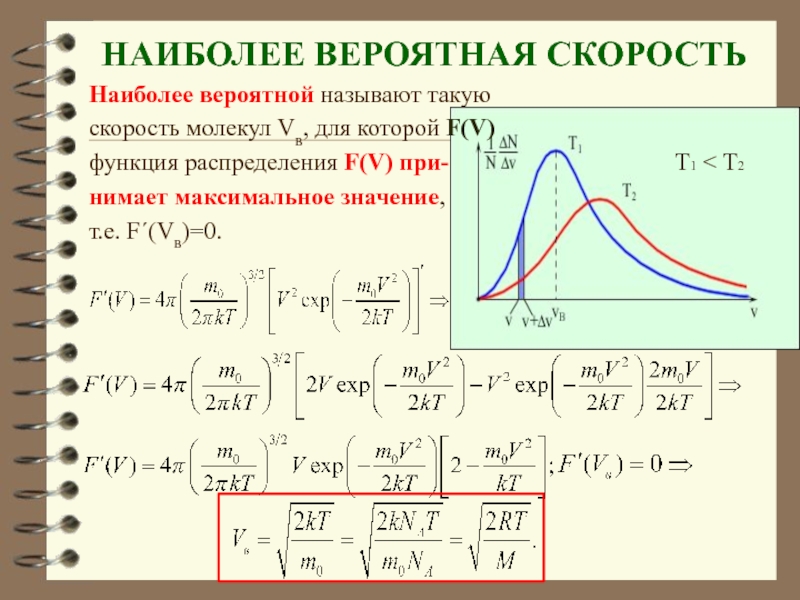
Слайд 64НАИБОЛЕЕ ВЕРОЯТНАЯ СКОРОСТЬ
Наиболее вероятной называют такую
скорость молекул Vв, для которой
F(V)
функция распределения F(V) при-
Т1 < Т2
нимает максимальное значение,
т.е. F΄(Vв)=0.
Слайд 65 Величина скорости, на которую при-ходится максимум зависимости
называют наиболее вероятной скоростью
. Величину этой скорости находят из условия равенства нулю производной:
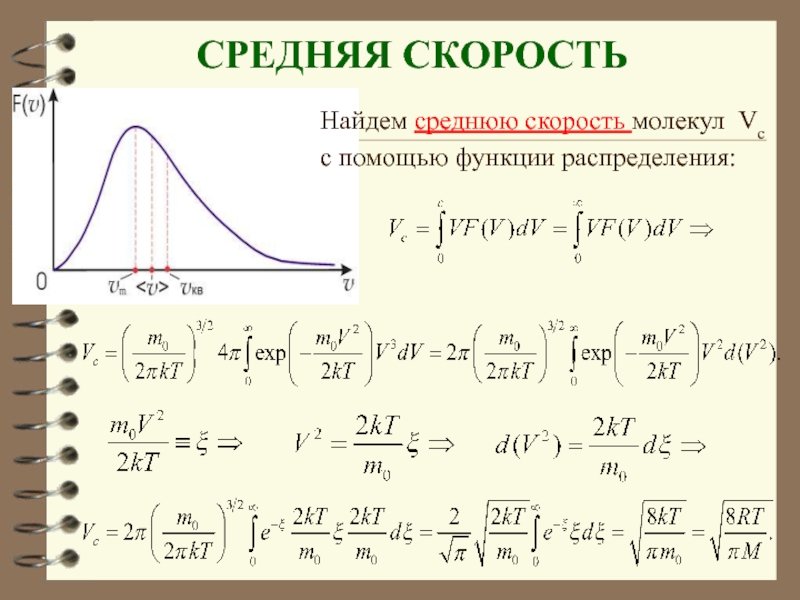
Слайд 66 СРЕДНЯЯ СКОРОСТЬ
Найдем среднюю скорость молекул Vc
с помощью функции распределения:
Слайд 67 Средняя скорость υср
где
– число молекул со скоростью от υ до . Если подставить сюда F(υ) и вычислить, то получим:
или
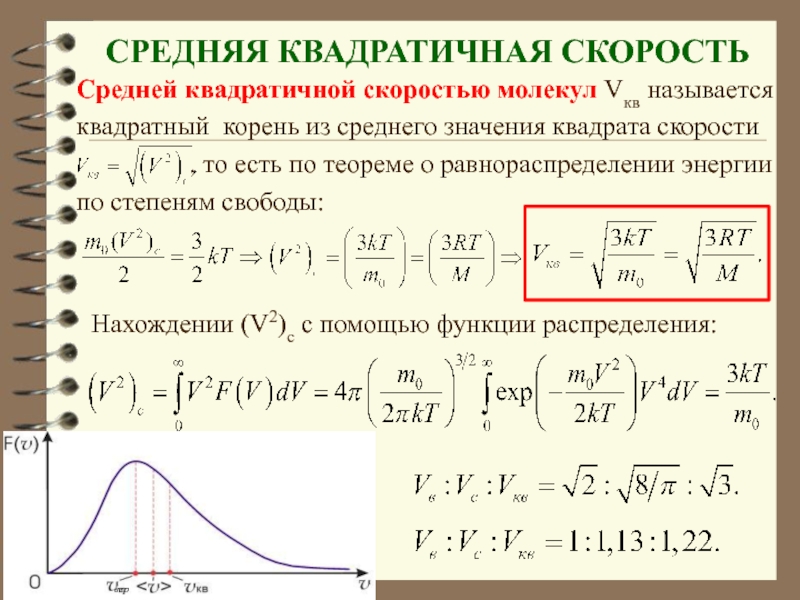
Слайд 68 СРЕДНЯЯ КВАДРАТИЧНАЯ СКОРОСТЬ
Средней квадратичной скоростью молекул Vкв называется
квадратный корень
из среднего значения квадрата скорости
, то есть по теореме о равнораспределении энергии
по степеням свободы:
Нахождении (V2)c с помощью функции распределения:
вер
Среднюю квадратичную скорость находят используя соотношение :
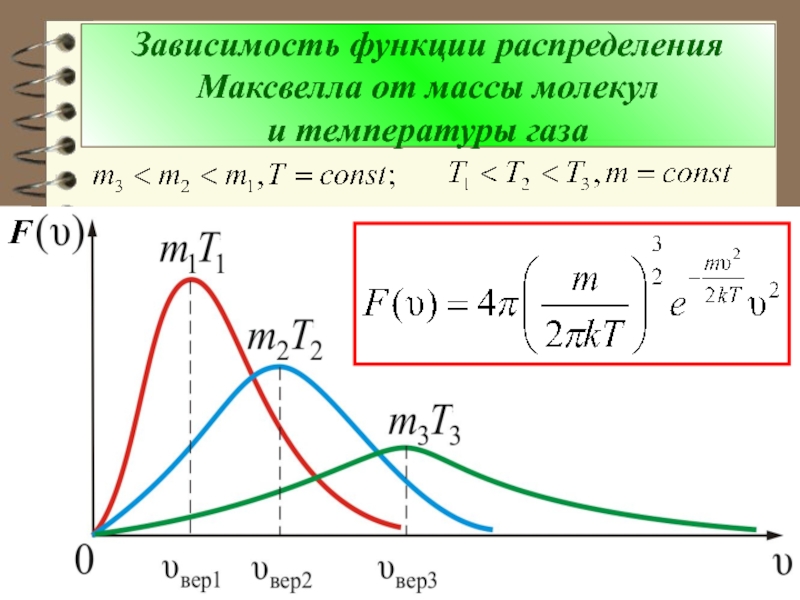
Слайд 72Зависимость функции распределения Максвелла от массы молекул
и температуры газа
F
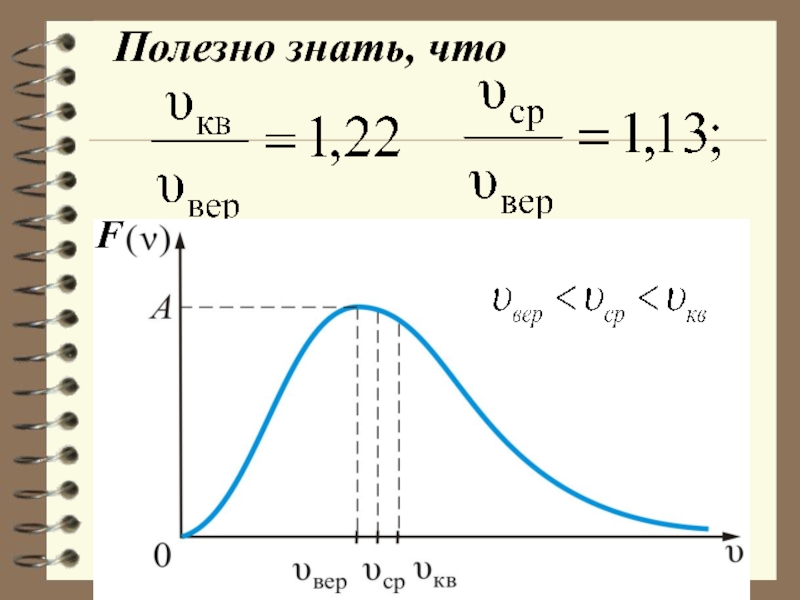
Слайд 73 Из рис. можно проследить за измене-нием
при изменении m и T:
(при ) или (при
).
Площадь под кривой величина посто-янная, равная единице ( ), поэтому важно знать как будет изменяться положение максимума кривой: