Слайд 1Термодинамика и статистическая физика
Слайд 2 Лекция № 6
Термодинамика реального газа.
1. Уравнение Ван-дер-Ваальса. Изотермы
газа Ван-дер-Ваальса. Критическая точка.
2. Метастабильные и абсолютно неустойчи-вые состояния.
3. Критерий термодинамической устойчи-вости. Принцип Ле Шателье-Брауна.
Как известно, уравнение состояния устанавливает связь между давлением Р,
объемом V, температурой T и числом молей ν газа в состоянии равновесия.
или
Уравнение Менделеева – Клапейрона - самое простое, надежное и известное уравнение состояния идеального газа.
Реальные газы описываются уравнением состояния идеального газа только приближенно, и отклонения от идеального поведения становятся заметными при высоких давлениях и низких температурах, особенно когда газ близок к конденсации.
Слайд 5При давлении 500 МПа объем молекул уже составит половину всего
объема газа. Таким образом, при высоких давлениях и низких температурах
указанная модель идеального газа непригодна.
При рассмотрении реальных газов - газов, свойст-ва которых зависят от взаимодействия молекул, на-до учитывать силы межмолекулярного действия.
Они проявляются на расстояниях ≤10-9 м и быстро убывают при увеличении расстояния между моле-кулами. Эти силы короткодействующие.
В 1 м3 газа при нормальных условиях содержится 2,68·1025 молекул, занимающих объем примерно
10-4 м3 (радиус молекулы примерно 10-10м), которым по сравнению с объемом газа можно пренебречь.
Слайд 6 Для газов с низкой температурой сжижения (He, H2, Ne и
даже N2, O2, Ar, CO, CH4) при давлениях до 50
атм отклонения не превышают 5%, а при давлениях до 10 атм 2%.
Легко конденсирующиеся газы (CO2, SO2, Cl2, CH3Cl) уже при 1 атм обнаруживают отклонения до 2 – 3%.
Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа.
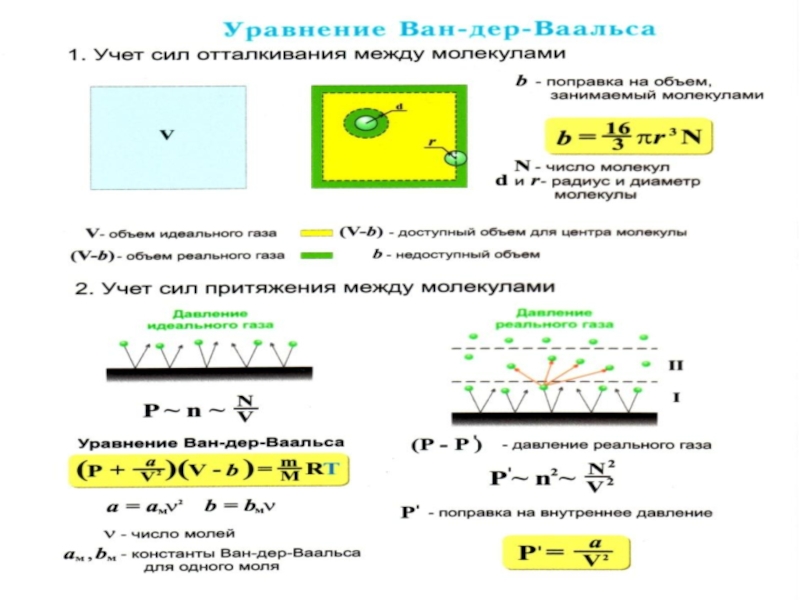
Слайд 7 Первая поправка в уравнении состояния идеального газа
рассматривает собственный объем, занимаемый молекулами реального газа. В уравнении Дюпре
(1864):
постоянная b учитывает собственный объем молекул.
Слайд 8По мере развития представлений о строении атома и квантовой механики,
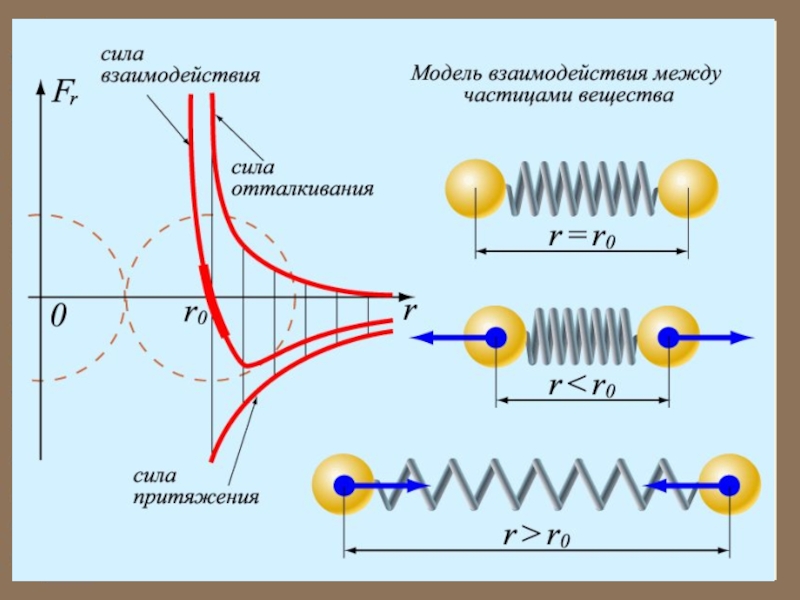
было выяснено, что между молекулами вещества одновременно действуют силы притяжения
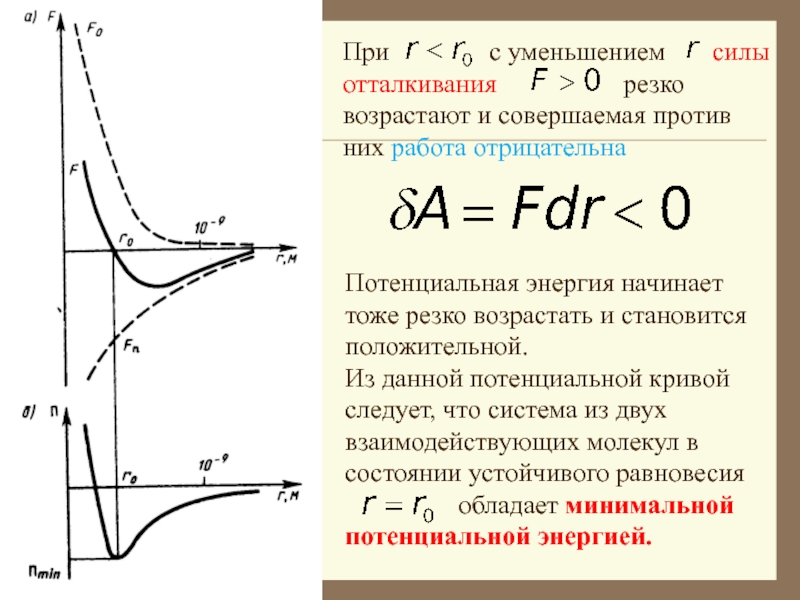
и силы отталкивания. На рисунке приведена качественная зависимость сил межмолекулярного взаимодействия от расстояния между молекулами, где и
соответственно силы отталкивания и притяжения, а - их результи-рующая. Силы отталкивания счита-ются положительными, а силы притяжения -отрицательными.
Коэффициенты и зависят от химической природы газов.
м межмолекулярные силы взаимодействия практически отсутствуют
.
При преобладают силы отталкивания .
Таким образом, расстояние со-ответствует расстоянию между молекулами, на котором бы они находились в отсутствии теплового движения.
На расстоянии результи-рующая сила , т.е. силы притяжения и отталкивания уравновешивают друг друга.
При - силы притяжения .
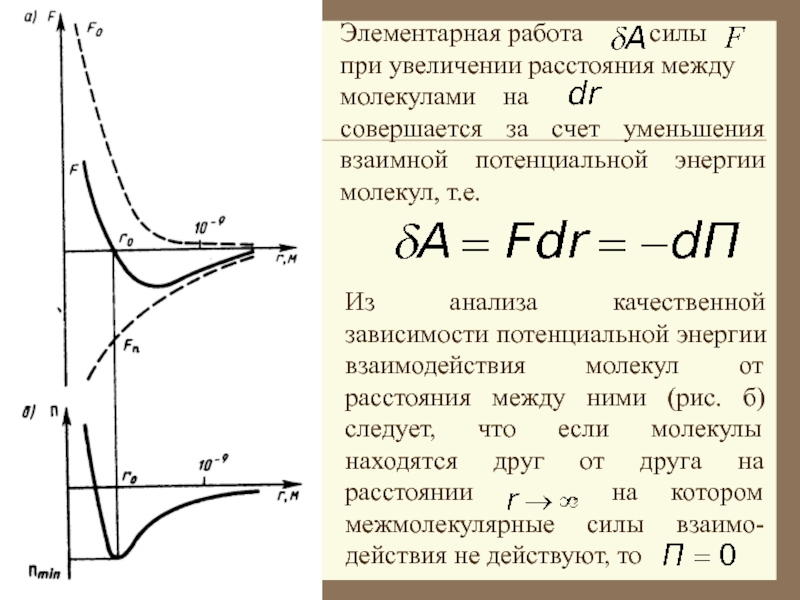
Слайд 11Из анализа качественной зависимости потенциальной энергии взаимодействия молекул от расстояния
между ними (рис. б) следует, что если молекулы находятся друг
от друга на расстоянии , на котором межмолекулярные силы взаимо-действия не действуют, то
Элементарная работа силы при увеличении расстояния между молекулами на
совершается за счет уменьшения взаимной потенциальной энергии молекул, т.е.
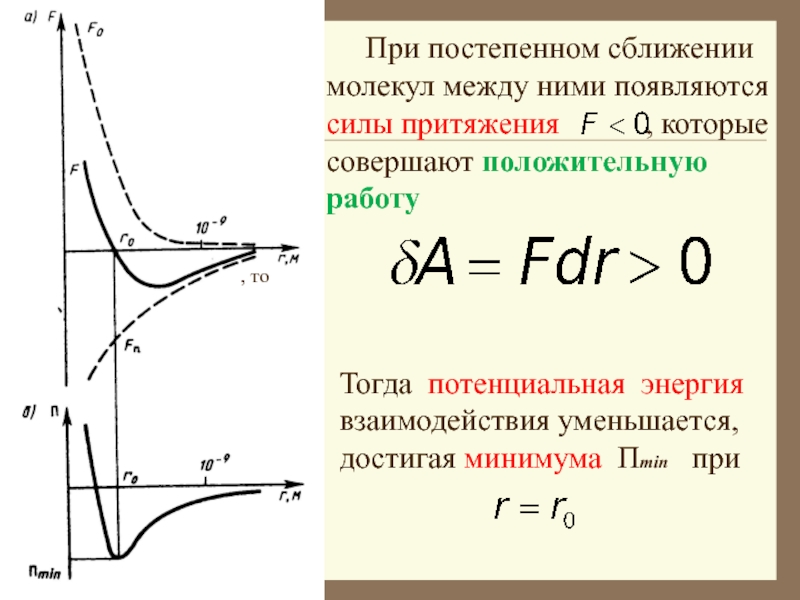
Слайд 13 При постепенном сближении молекул между ними появляются
силы притяжения , которые совершают
положительную работу
, то
Тогда потенциальная энергия взаимодействия уменьшается,
достигая минимума Пmin при
Слайд 14Потенциальная энергия начинает тоже резко возрастать и становится положительной.
Из данной
потенциальной кривой следует, что система из двух взаимодействующих молекул в
состоянии устойчивого равновесия
обладает минимальной потенциальной энергией.
При с уменьшением силы отталкивания резко возрастают и совершаемая против них работа отрицательна
Слайд 15 - наименьшая потенциальная энергия
взаимодействия молекул – определяет работу, которую нужно совершить против сил
притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии
- определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы хаотического (теплового) движения молекул.
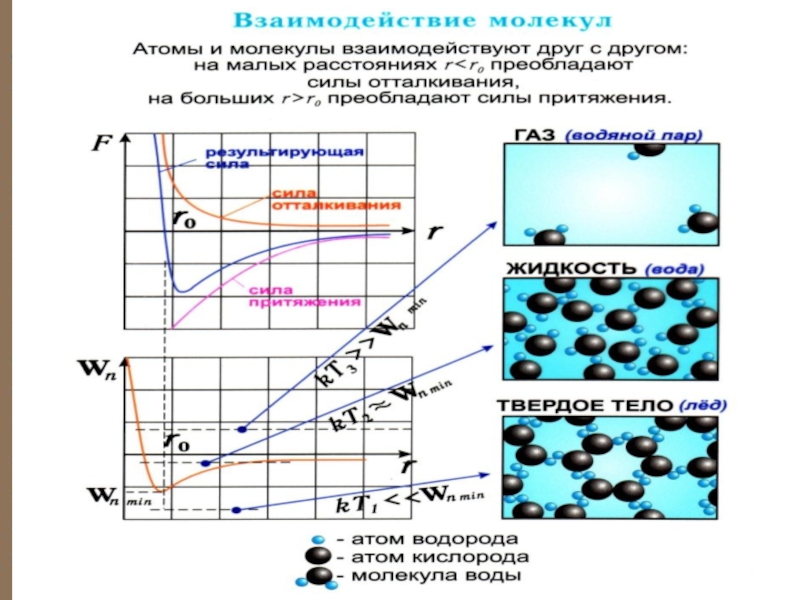
Критерием различных агрегатных состояний вещества является соотношение между величинами и .
Формула Ленарда-Джонса
то вещество находится в жидком состоянии, так как в результате
теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее .
Если , то вещество находится в газооб-разном состоянии, так как интенсивное тепловое движение молекул препятствует соединению молекул, сблизившихся до расстояния , т.е. вероятность образвания агрегатов из молекул достаточна мала.
Если , то вещество находится в твердом состоянии, так как молекулы, притягиваясь друг к другу, не могут удалиться на значительные расстояния и колеблются около положений равновесия, определяемого расстоянием .
Слайд 17 Таким образом, любое вещество в зависимости от температуры
может находиться в газообразном, жидком или твердом агрегатном состоянии, причем
температура перехода из одного агрегатного состояния в другой зависит от значения для данного вещества.
Например, у инертных газов мало, а у металлов велико, поэтому при обычных (комнатных) температурах они находятся соответственно в газообразном и твердом состояниях.
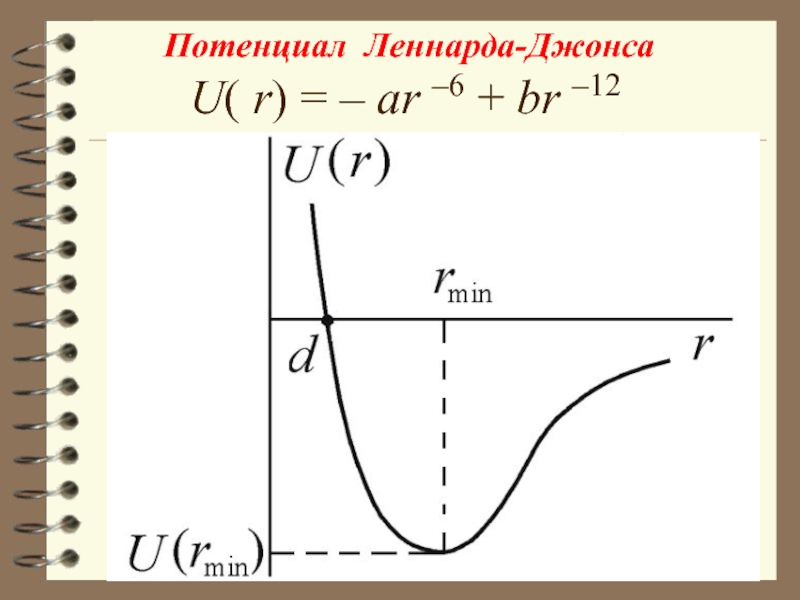
Слайд 18U( r) = – ar –6 + br –12
Потенциал
Леннарда-Джонса
Слайд 19Джон Эдвард Леннард-Джонс (англ. sir John Edward Lennard-Jones;27 октября 1894-1
ноября 1954) — английский физик- и химик-теоретик. Член Лондон-ского королевского
общества (1933). Научные труды Леннарда-Джонса посвящены квантовой химии, статистичес-
В 1924 году предложил полуэмпирический потенциал для описания межатомных сил (потенциал Леннарда-Джонса).
кой механике, атомной физике.
Слайд 20 Вывод уравнения Ван-дер-Ваальса
Уравнение Ван-дер-Ваальса – одно
из первых уравнений состояния реального газа, которое было предложено в
1873 г. голландским физиком Ван-дер-Ваальсом. Данное уравнение учитывает конечные размеры всех молекул, что становится существенным при больших давлениях, а также притяжение молекул в результате межмолекулярного взаимодействия.
Слайд 21 Ян Дидерик
Ван-дер-Ваа́льс
(23 ноября 1837, Лейден
— 8 марта 1923, Амстердам) — голландский физик, лауреат Нобелевской
премии по физике в 1910 г. Работы Ван-дер-Ваальса относятся к области теоретической молекулярной физики.
Слайд 22 Учет собственного
объема молекул.
Наличие сил отталкивания, которые противодей-ствуют
проникновению в занятый молекулой объ-ём других молекул, сводится к тому, что фактичес-кий свободный объем, в котором могут двигаться молекулы реального газа, будет не , а ,
где - объем, занимаемый самими молекулами.
Покажем, что объем равен учетверенному собственному объему молекул.
Если - диаметр молекулы, то каждая молеку-ла реального газа имеет объем .
Слайд 23Если, например, в сосуде находятся две молекулы, то центр любой
из них не может приблизиться к центру другой молекулы на
расстояние , меньшее диаметра молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса ,
т.е.
Запрещенный объем равен восьми объемам молекулы или учетверенному объему молекулы в пересчете на одну молекулу. Для одного моля газа . Объем, доступный точечным молекулам, будет равен V b .
Слайд 24Если в сосуде находится один моль газа, то уравнение состояния
примет вид (N = NA, NAk = R, b =
4NAVмолек)
P(V b) = RT.
Для = m/ молей газа уравнение состоя-ния газа с учетом конечного размера молекул примет вид:
P(V b) = RT.
Отметим, что это уравнение является приближенным и выведено в предположе-нии только парных столкновений.
Слайд 25 Рассмотрим влияние сил притяжения на уравнение состояния идеального
газа.
Будем считать для простоты частицы газа точечными.
Наличие между
ними сил притяжения, действующих на больших расстояниях, приводит к появлению дополнительного внутреннего воздействия на газ.
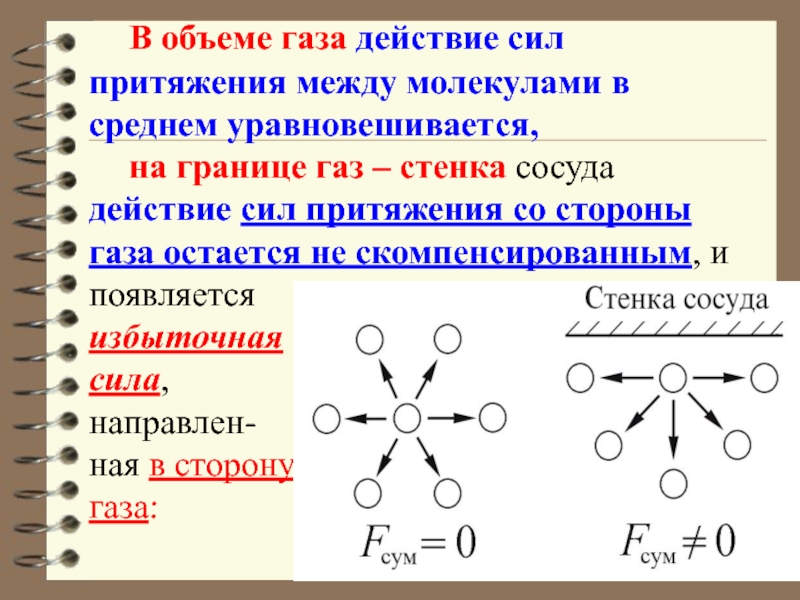
Слайд 26 В объеме газа действие сил притяжения между молекулами в среднем
уравновешивается,
на границе газ – стенка сосуда действие сил притяжения
со стороны газа остается не скомпенсированным, и появляется
избыточная
сила,
направлен-
ная в сторону
газа:
Слайд 27 Дополнительное внутреннее давление Рвнутр пропорционально числу частиц, приходящихся на
единицу площади границы nS и силе взаимодействия этих частиц с
другими частицами газа, находящимися в еди-нице объема nV : Pвнутр ~ nS nV
И поэтому будет пропорционально квадрату концентрации числа частиц:
Pвнутр ~ N 2/V 2
где N – полное число частиц в сосуде объема V.
Слайд 28 Если N = NA – в сосуде
находится один моль газа, то запишем:
Pвнутр = a/Vm 2 ,
где а – постоянная величина, характе-ризующая силы межмолекулярного притяжения, своя для каждого сорта газа. - молярный объём.
В случае -молей с учётом
, получаем:
Pвнутр = 2a/V 2 .
Слайд 29 С учетом внутреннего давления уравнение состояния примет вид:
(P + 2 a/V 2)V = RT
Давление Pвнутр не зависит от материала стенки, в противном случае удалось бы создать вечный двигатель первого рода.
Слайд 30 Учитывая совместное действие сил притяжения и сил отталкивания и получен-ные
поправки для объема и давления в урав-нении Менделеева-Клапейрона,получим ура-внение Ван-дер-Ваальса
для реального газа:
(P + 2 a/V 2)(V b) = RT
Данное уравнение справедливо при условии: b << V и 2a/V 2 << P.
Помимо этого предполагается, что частицы газа сферически симметричны. Поскольку реально это не так, то даже для неплотных газов величины а и
b зависят от температуры.
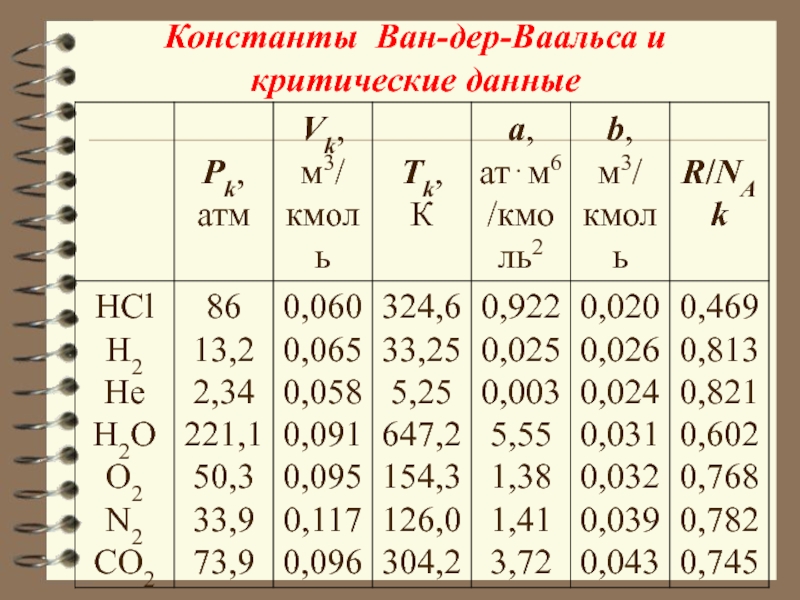
Слайд 31Константы Ван-дер-Ваальса и критические данные
Слайд 33 Изотермы уравнения Ван-дер-Ваальса
Проанализируем изотермы уравнения Ван-дер-Ваальса – зависимости Р
от V для реального газа при постоянной температуре.
(P + 2 a/V 2)(V b) = RT.
Умножив уравнение Ван-дер-Ваальса на V 2 и раскрыв скобки, получим:
PV 3 – (RT + bP) V 2 + a2V ab3= 0
Слайд 34 Поскольку данное уравнение имеет третью степень относительно V,
а коэффициенты при V действительны, то оно имеет либо один,
либо три вещественных корня – т.е. изобара Р = const пересекает кривую Р = Р(V) в одной или трех точках. Причем с повы-шением температуры мы перейдем от немонотонной зависимости Р = Р(V)
к монотонной однозначной функции.
Слайд 35 Поскольку в критической точке все три корня совпадают
и равны , уравнение приводится к
виду:
или
Т.к. первое и последнее уравнения тождественны, то в них должны быть равны и коэффициенты при неизвестных соответствующих степеней. Поэтому можно записать:
Для одного моля последнее уравнение будет:
Слайд 36Решая полученные уравнения, найдем:
, м3
, МПа
, К
Кислород 9,54.10-5
5,03
154
Азот 11,76.10-5 3,39 126
Газ
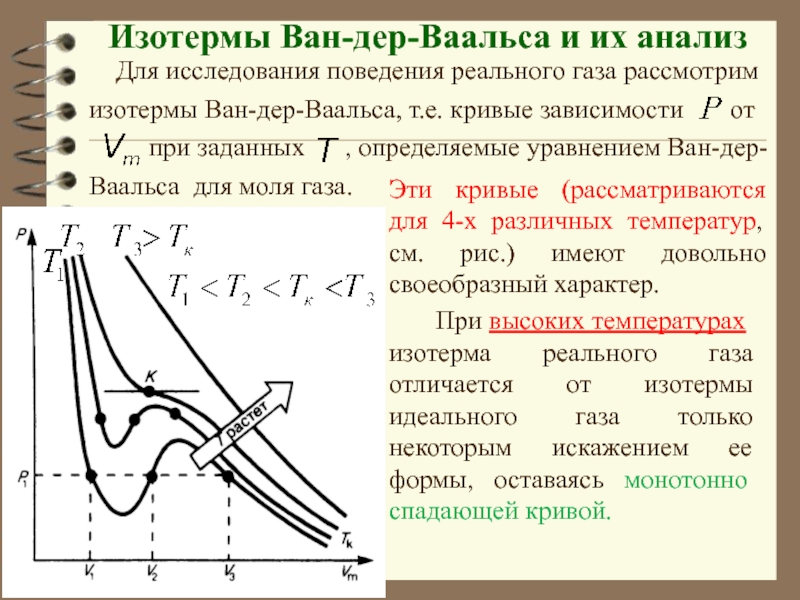
Слайд 37Изотермы Ван-дер-Ваальса и их анализ
Для исследования поведения реального
газа рассмотрим изотермы Ван-дер-Ваальса, т.е. кривые зависимости
от
при заданных , определяемые уравнением Ван-дер-Ваальса для моля газа.
Эти кривые (рассматриваются для 4-х различных температур, см. рис.) имеют довольно своеобразный характер.
При высоких температурах
изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой.
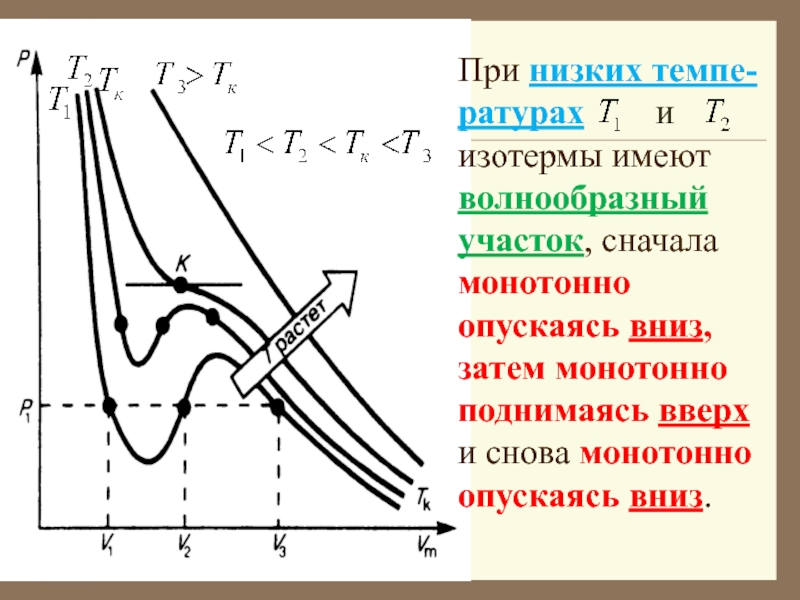
Слайд 38При низких темпе-ратурах и изотермы имеют
волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх
и снова монотонно опускаясь вниз.
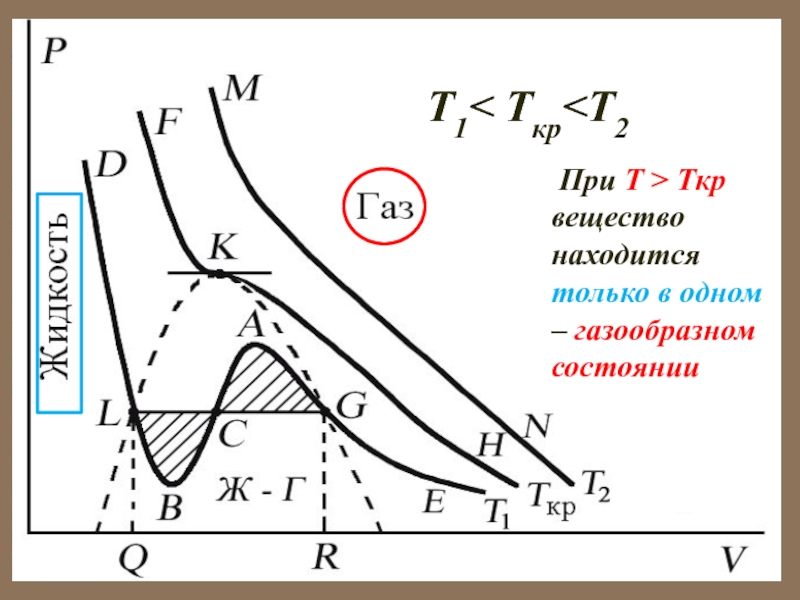
Слайд 39T1< Tкр Tкр вещество находится только в
одном – газообразном состоянии
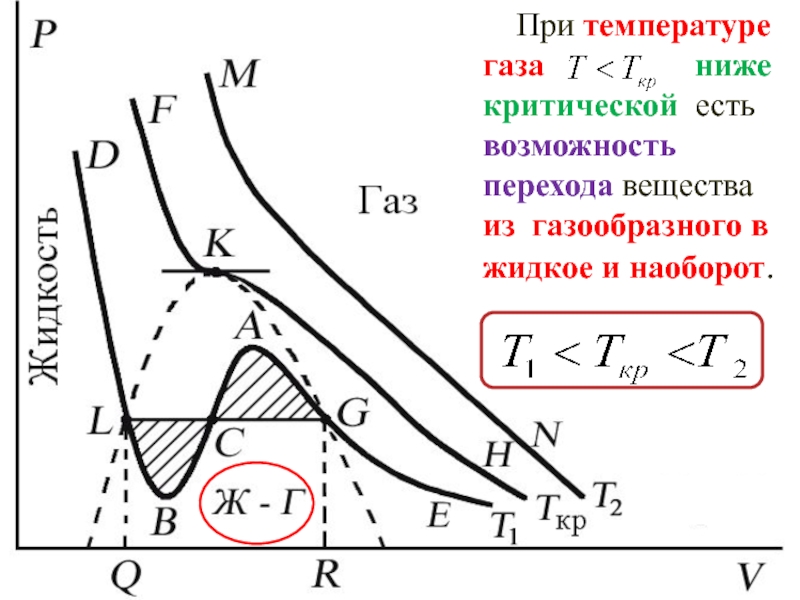
Слайд 40 При температуре газа ниже критической есть возможность перехода
вещества из газообразного в жидкое и наоборот.
На участке BCA
изотермы Т1 давление растет с увеличением объема (dP/dV) > 0. Данное состояние абсо- лютно неустойчиво, поскольку здесь должны усиливаться малейшие флуктуации плотности.
Слайд 41 При температуре газа
ниже критической есть возможность перехода вещества
из газообразного в жидкое и наоборот.
>
>
Слайд 42 Поэтому область ВСА не может устойчиво существовать (
неустойчива).
В областях DLB и AGE давление падает с увеличением
объема (dP/dV)Т < 0 – это необходимое, но не достаточное условие устойчивого равновесия.
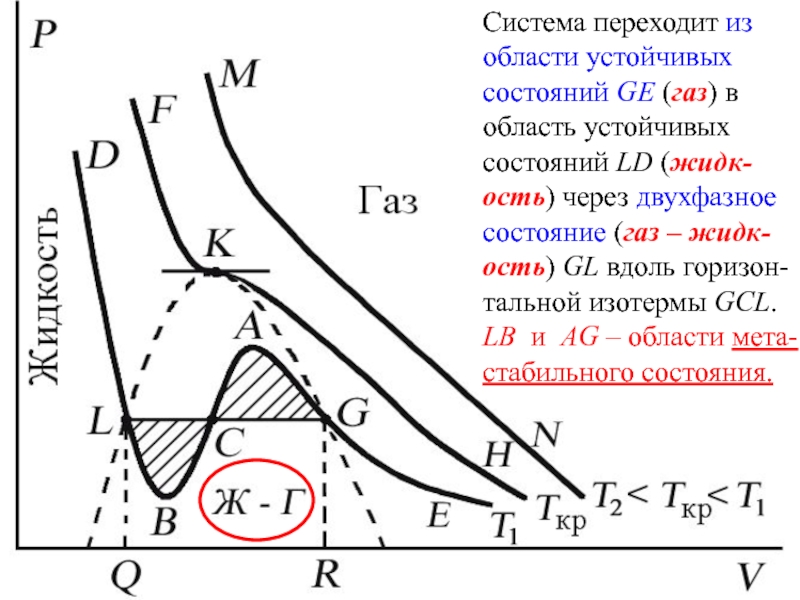
Эксперимент показывает, что система переходит из области устойчивых состояний GE (газ) в область устойчивых состояний LD (жидкость) через двухфазное состояние (газ – жидкость) GL вдоль горизонтальной изотермы GCL.
Слайд 43Система переходит из области устойчивых состояний GE (газ) в область
устойчивых состояний LD (жидк-ость) через двухфазное состояние (газ – жидк-ость)
GL вдоль горизон-тальной изотермы GCL.
LB и AG – области мета- стабильного состояния.
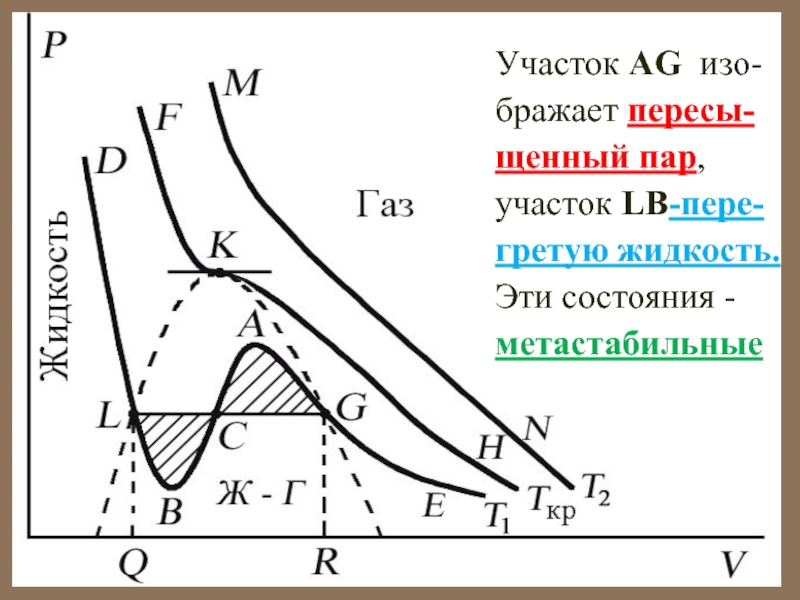
Слайд 44Участок AG изо-бражает пересы-щенный пар,
участок LB-пере-гретую жидкость.
Эти состояния -
метастабильные
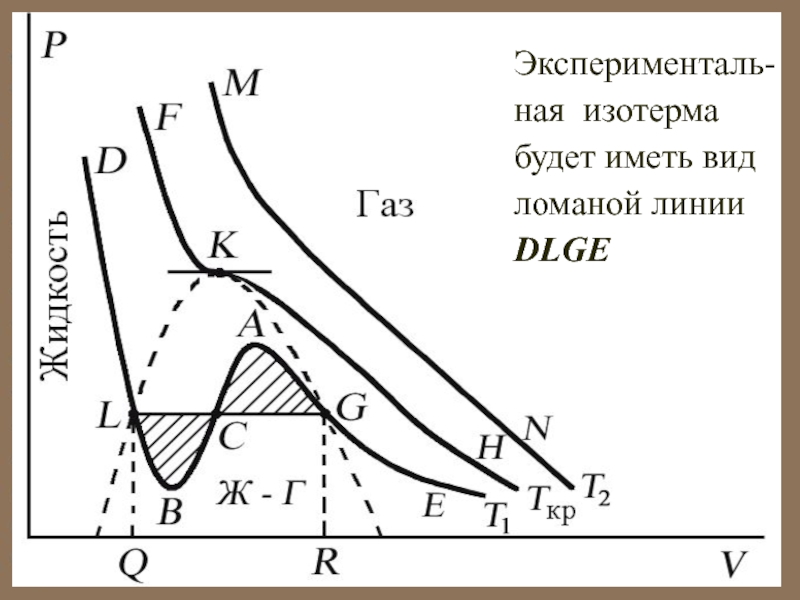
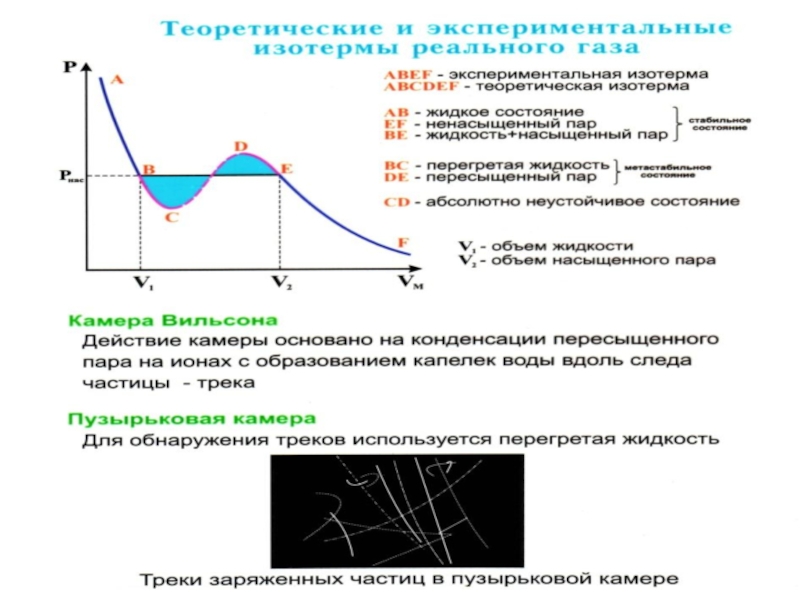
Слайд 45Эксперименталь-ная изотерма будет иметь вид ломаной линии DLGE
Слайд 46 При квазистатическом сжатии, начиная с точки G, система
распадается на 2 фазы – жидкость и газ, причем плотности
жидкости и газа остаются при сжатии неизменными и равными их значениям в точках L и G соответственно.
При сжатии количество вещества в газообразной фазе непрерывно уменьша-ется, а в жидкой фазе – увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние.
Слайд 47 Если через крайние точки горизонтальных участков семейства изотерм
провести линию, то получится колоколообразная кривая (см. рис.), ограничивающая область
двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от
нее находится область жидк-
ого состояния, а справа – обл-
асть пара. Пар отличается от
всех остальных газообразных
состояний тем, что при изотер-
мическом сжатии претерпевает
процесс сжижения. Газ при
температуре выше критической не может
быть превращен в жидкость ни при каком давлении.
Слайд 48 Наличие критической точки на изотерме Ван-дер-Ваальса означает, что для каждой
жидкости существует такая темпера-тура, выше которой вещество может существовать только
в газообразном состоянии.
К этому заключению пришел и Д.И. Менделеев в 1861 г. Он заметил, что при определенной температуре прекращалось поднятие жидкости в капиллярах, т.е. поверхностное натяжение обращалось в нуль. При той же температуре обращалась в нуль скрытая теплота парообразования.
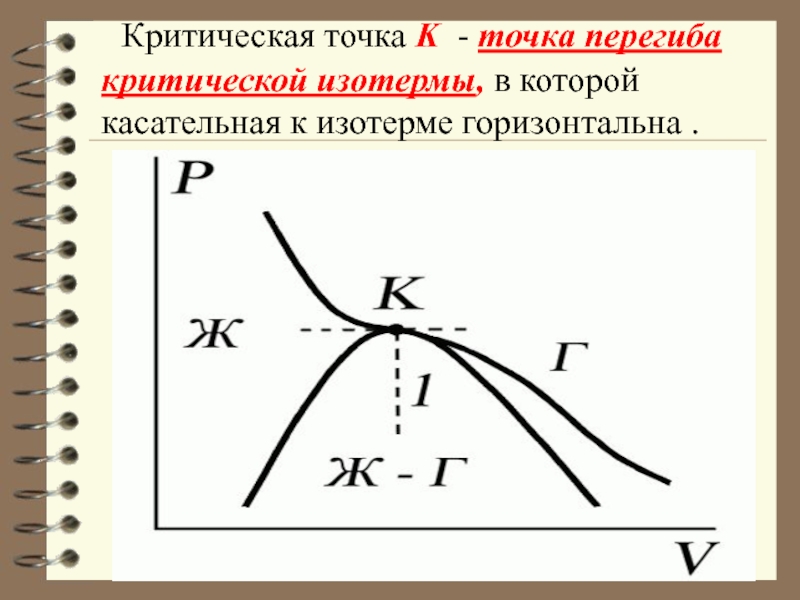
Слайд 49 Критическая точка K - точка перегиба критической изотермы, в
которой касательная к изотерме горизонтальна .
Слайд 51 Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:
1) Уравнение
было получено из модельных представлений о свойствах реальных газов и
жидкостей, а не явилось результатом эмпирического подбора функции f(P,V,T), описывающей свойства реальных газов;
Слайд 52 2) Уравнение долго рассматривалось как некоторый общий вид уравнения
состо-яния реальных газов, на основе которого было построено много других
уравнений состояния;
3) С помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализи-ровать критические явления.
В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме.
Слайд 53 Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию
молекул в газовой фазе, которую не удается описать, учитывая зависимость
параметров a и b от объема и температуры, без использования дополнительных постоянных.
После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных.
Слайд 54 Две модификации уравнения предложил Клаузиус, и обе они связаны с
усложнением вида постоянной b. Больцман получил три уравнения этого типа,
изменяя выражения для постоянной a.
Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости.
Слайд 55 Принцип Ле Шателье-Брауна
Принцип Ле Шателье-Брауна
позволяет предвидеть направление течения процесса в системе, когда она выведена
внешним воздействием из состояния устойчивого равновесия. Если система находится в устойчивом равновесии, то всякий процесс, вызванный в ней внешним воздействием или другим первичным процессом, всегда бывает направлен таким образом, что он стремиться уничтожить изменения, произведённые внешним воздействием или первичным процессом.
Слайд 56 Превращение любого газа в жидкость – сжижение газа – возможно
лишь при температуре ниже критической.
Критические температуры
Сжижение газов
Слайд 59 Основные результаты
Уравнение
Ван-дер-Ваальса для произ-вольного количества вещества реального газа учитывает конечный
объем молекул b и их притяжение между собой 2a/V 2:
где а и b – постоянные Ван-дер-Ваальса,
V – объем, занимаемый газом,
P – давление газа на стенки сосуда.