Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТНиС 06
Содержание
- 1. ТНиС 06
- 2. Влажный воздух Влажный воздух – это смесь
- 3. Абсолютная и относительная влажности воздуха Абсолютная
- 4. Влагосодержание влажного воздуха Влагосодержание воздуха – это
- 5. Hd-диаграмма влажного воздуха С учетом газовых
- 6. К Hd-диаграмме Hd-диаграмма была предложена профессором Л.К.
- 7. Процессы в Hd-диаграмме Цифры на оси ординат
- 8. I закон термодинамики для потока
- 9. Работа проталкивания Для ввода 1 кг/с в
- 10. Составляющие работы Работа на изменение кинетической энергии
- 11. Последние составляющие работы В общем случае, между
- 12. Уравнение I закона термодинамики для потока
- 13. Изменения потенциальной и кинетической энергий газа Для газов gdz
- 14. I закон термодинамики для обратимого, адиабатного
- 15. Истечение газов и паров через суживающиеся сопла
- 16. Соотношения между параметрами Для адиабатного процесса: p1v1k=pvk,
- 17. Скорость истечения газа Вынесем за скобки первый
- 18. Массовый расход газа При адиабатном истечении p1v1k=p2v2k,
- 19. К гипотезе Сен-Венана и Вентцеля
- 20. Исследование на экстремум Чтобы найти mmax ,
- 21. Критическое отношение давлений Если в выражение (7)
- 22. Критическая скорость истечения Подставив βкр в формулу
- 23. Гипотеза Сен-Венана и Вентцеля ● сc; р2>ркр р’2
- 24. Гипотеза Сен-Венана и Вентцеля ● c=cкр
- 25. Комбинированное сопло (Лаваля) Комбинированное из сужающейся
- 26. Режимы истечения Отношение β Суживающееся сопло Сопло Лаваля β>βкр c
- 27. Скорость истечения пара Скорость необратимого
- 28. Истечение газов с учетом трения Из-за
- 29. Дросселирование газов и паров Если при
- 30. Дросселирование – условно изоэнтальпийный процесс Потери
- 31. Дросселирование газов Изменение
- 32. Температура инверсии На предыдущем слайде изображено дросселирование
- 33. Использование дросселирования для ожижения газов Снижение температуры газа при дросселировании, если tнач
- 34. Дросселирование (мятие) пара Если мятию подвергается
- 35. Снижение работоспособности пара при дросселировании Из
- 36. Опыт Джоуля-Томсона В физике дросселирование пара
- 37. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ТНиС 06
● Влажный воздух
● I закон термодинамики для потока
● Истечение
газов и паров
© НГТУ, 2014Слайд 2Влажный воздух
Влажный воздух – это смесь сухого воздуха и
водяного пара.
По закону Дальтона для смеси газов
B=pв+pп,
где
В – барометрическое (атмосферное) давление,рв и рп – соответственно парциальные давления
сухого воздуха и водяного пара.
При: рп<рн – воздух влажный, ненасыщенный;
рп=рн – воздух влажный насыщенный водяным паром.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 3Абсолютная и относительная
влажности воздуха
Абсолютная влажность воздуха –
это масса пара в 1 м³
влажного воздуха, что совпадает
с определением плотности пара при его парциальном давлении ρп, кг/м³.
Относительная влажность воздуха – это отношение его
абсолютной влажности к максимально возможной в
состоянии насыщения φ=ρп/ρн.
С учетом того, что ρп/ρн=vн/vп, а по закону Бойля-Мариотта
рпvп=рнvн, имеем:
. (1)
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 4Влагосодержание влажного воздуха
Влагосодержание воздуха – это масса водяного пара,
приходящаяся на 1 кг сухого воздуха d=mп/mв.
Запишем уравнение
Клапейрона для водяного пара и сухого воздуха: pпV=mпRпT; pвV=mвRвT.
Поделив уравнения Клапейрона и разрешив относительно
влагосодержания, имеем:
.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
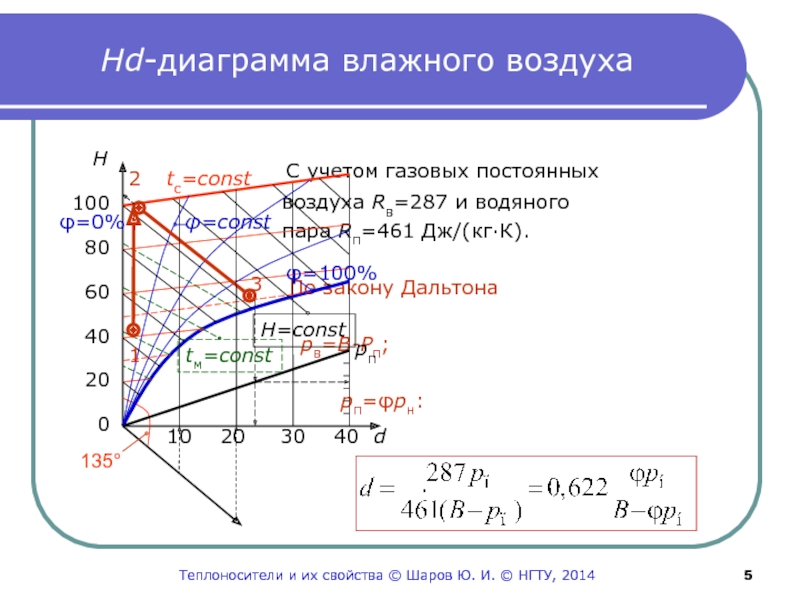
Слайд 5Hd-диаграмма влажного воздуха
С учетом газовых постоянных
воздуха Rв=287 и водяного
пара Rп=461 Дж/(кг·К).
По закону Дальтона рв=В-Рп;
рп=φрн:
.
135
H
100
80
60
40
20
0
10 20 30 40 d
pп
1
2
3
H=сonst
tм=сonst
tc=сonst
φ=сonst
φ=100%
φ=0%
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 6К Hd-диаграмме
Hd-диаграмма была предложена профессором Л.К. Рамзиным
в
1918 году.
Она удобна для исследования процессов влажного
воздуха
в кондиционерах, сушильных установках и т.д.Оси ординат и абсцисс в ней находятся под углом 135.
Но значения влагосодержаний d, г. пара/(кг сух. возд.),
для удобства, сносятся на горизонталь.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 7Процессы в Hd-диаграмме
Цифры на оси ординат – это температуры
сухого воздуха, С
и энтальпии влажного воздуха Н=hв+dhп, кДж/(кг
сух. возд.)Относительная влажность влажного воздуха:
● на оси ординат φ=0 % – сухой воздух,
● на линии φ=100 % – влажный, насыщенный воздух.
Процессы:
1-2 нагрев воздуха в калорифере при d=сonst,
2-3 сушка материала воздухом при H=сonst.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 8I закон термодинамики для потока
1 кг/с газа в сечениях I и II
перемещается
на расстояние s1 и s2.
К газу подведена теплота qвн.
По I закону термодинамики
q=qвн+qтр=Δu+l, (1)
где qтр – потери на трение, перешедшие в теплоту.
I(p1,v1,T1)
f1
f2
c1
c2
s1
z1
s2
z2
II(p2,v2,T2)
qвн
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 9Работа проталкивания
Для ввода 1 кг/с в сечение I,
надо совершить работу
lI=-p1f1s1=-p1v1.
В сечении II газ
совершит работу lII=p2f2s2=p2v2.
Их разность – работа проталкивания:
l1=lII-lI=p2v2-p1v1. (2)
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 10Составляющие работы
Работа на изменение кинетической энергии потока:
l2=с22/2-с12/2,
(3)
где с1 и с2 – скорости газа в сечениях I
и II, м/с.Работа на изменение потенциальной энергии газа:
l3=g(z2-z1), (4)
где z1 и z2 – высота осей канала над горизонталью, м.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 11Последние составляющие работы
В общем случае, между сечениями I и
II газ может
совершать техническую работу lт; (5)
для реального газа надо
учесть и потери на трение lтр. (6)После подстановки выражений (2)-(6) в (1) имеем:
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 12Уравнение I закона термодинамики
для потока
Так как lтр=qтр, то
они сокращаются.
Перегруппируем члены полученного уравнения;
учтем, что
u2+p2v2=h2
и u1+p1v1=h1:
.
Запишем это выражение в дифференциальной форме для
потока, не совершающего техническую работу:
dq=dh+cdc+gdz.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 13Изменения потенциальной и кинетической энергий газа
Для газов gdz
то есть можно считать gdz≈0, тогда
выражение I закона термодинамики
для обратимого и необратимого адиабатного потока (dq=0):
cdc=-dh. (7)
Для обратимого, адиабатного изменения состояния рабочего
тела воспользуемся первым законом термодинамики.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 14I закон термодинамики
для обратимого, адиабатного потока
Аналитическое выражение I
закона термодинамики для
обратимого, адиабатного изменения состояния:
dq=0 =du+pdv, откуда du=-pdv.
Подставим это выражение в (7):
cdc=-d(u+pv)=-du-pdv-vdp=pdv-pdv-vdp=-vdp.
Итак, выражение I закона термодинамики для обратимого
адиабатного потока:
cdc=-vdp. (8)
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 15Истечение газов и паров
через суживающиеся сопла
Рассмотрим
обратимое, адиабатное
истечение газа через суживающееся
сопло.Для этого случая применимо выра-
жение (8) I закона термодинамики:
cdc=-vdp. (1)
или в интегральной форме:
.
Так как c1<
I(p1,T1,c1)
II(p2,T2,c2)
Сопло
Поршень
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 16Соотношения между параметрами
Для адиабатного процесса:
p1v1k=pvk,
или
p11/kv1=p1/kv.
Выразим удельный объем из уравнения адиабаты и
подставим под
знак интеграла: .
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 17Скорость истечения газа
Вынесем за скобки первый член и
найдем скорость
обратимого истечения газа:
. (2)
Для установившегося течения массовый расход газа является постоянным, то есть его уравнение неразрывности
для выходного сечения сопла, кг/с:
m=cf/v2=const. (3)
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 18Массовый расход газа
При адиабатном истечении
p1v1k=p2v2k, откуда v2=v1(p1/p2)1/k.
(4)
Подставляем (4) и (2) в (3):
; (5)
. (6)Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 19К гипотезе Сен-Венана и Вентцеля
В формуле
расхода газа (6)
переменным является
выражение в квадратных
скобках.
Обозначим p2/p1=β,
тогда [β2/k-β(k+1)/k]=var.
При β=0 и β=1 m=0.
m
mmax
к
0
0,5
1 β
βкр
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 20Исследование на экстремум
Чтобы найти mmax , надо исследовать функцию
на экстремум,
то есть:
.
Поделим выражение на β(2-k)/k(k+1)/k, получим
2/(k+1)=βкр(k-1)/k,
откуда . (7)
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 21Критическое отношение давлений
Если в выражение (7) для βкр
подставить значения
показателей адиабаты k газов,
то получим:
● 1-атомные
газы k=1,67; βкр=0,49;● 2-атомные газы k=1,41; βкр=0,528;
● 3-атомные газы k=1,29; βкр=0,546.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 22Критическая скорость истечения
Подставив βкр в формулу (2), получим критическую
скорость истечения:
. (8)
Если
в (8) подставить р1=ркр/βкр; v1=vкрβкр1/k,
то:
. (9)
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 23Гипотеза Сен-Венана и Вентцеля ● с
Из формулы (9) следует, что
критическая скорость истечения
– это местная скорость звука (при
критических параметрах).
Гипотеза Сен-Венана и Вентцеля:
● с
(a-c)>0.
Через некоторое время устанавливается скорость
истечения c’>c;
р2>ркр р’2 с c Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 24Гипотеза Сен-Венана и Вентцеля
● c=cкр
● c=cкр:
относительная скорость (a-cкр)=0;
импульс разряжения никогда
не
дойдет до выходного сечения сопла; скорость истечения остается критической.
Если подставить (7) в (6), получим максимальный расход
газа через сопло:
. (10)
р2=ркр р’2 с=cкр (a-cкр)=0 c Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 25Комбинированное сопло (Лаваля)
Комбинированное из сужающейся
и расширяющейся
частей
сопло впервые применил шведский
инженер
Лаваль для получения сверхзвуковых скоростей истечения
водяного пара.
Угол φ расширяющейся части сопла
не должен превышать 12, чтобы получить сверхзвуковые
скорости истечения.
Длина расширяющейся части сопла
lр=(d2-dmin)/2tg(φ/2).
ркр р2
fmin lр f2
скр с>cкр
φ
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 26Режимы истечения
Отношение β Суживающееся сопло Сопло Лаваля
β>βкр c
β<βкр c=cкр c>cкр.
Действительная скорость всегда ниже теоретической из-за
необратимых потерь на трение и завихрение:
сд=φс,
где φ – скоростной коэффициент сопла.
Для хорошо спрофилированных и чисто обработанных сопел
φ=0,92…0,99.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 27Скорость истечения пара
Скорость необратимого истечения пара
можно найти из выражения (7) I закона
термодинамики в интегральной
форме, при условии:
с1<<с2; с1≈0; с2=с,
тогда: с2/2=h1-h2;
или .
Энтальпии пара в это уравнение надо подставлять в Дж/кг.
Критическая скорость истечения находится по аналогичной
формуле: .
p1=Const
p2=Const
T1=Const
h
h1
h2
s
1
2
hкр
pкр=Const
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 28Истечение газов с учетом трения
Из-за потерь части кинетической
энергии
газа на трение и завихрение
действительная скорость истечения ниже
теоретической:
сд=φс,
где φ – скоростной коэффициент сопла;
для хорошо спрофилированных и
обработанных сопел φ=0,92…0,99.
Потери кинетической энергии оцениваются коэффициентом
потери энергии ψ:
h
s
1
2
2д
ha
ψha
h1
h2
h2д
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 29Дросселирование газов и паров
Если при движении газа он
встречает
местные сужения (вентиль, шайба), то
происходит дросселирование.
В
месте сужения скорость газа возрастает, но затем она восстанавливается; давление
падает, но затем возрастает до р2<р1.
Дросселирование (мятие) – это процесс понижения давления при
прохождении газа через местное сужение.
Падение давления зависит от природы газа, скорости движения и
величины сужения. Этот эффект используется для измерения
скорости газа с помощью дроссельных шайб.
p h
l
p1
h1
p2
h2
∆p
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 30Дросселирование – условно
изоэнтальпийный процесс
Потери на трение превращаются в
теплоту, которая в
адиабатном процессе воспринимается газом.
По I
закону термодинамики для адиабатного процесса:или .
Скорости газа с2 и с1 мало отличаются, поэтому можно
принять с2~с1, то есть h2~h1.
Таким образом можно считать условно дросселирование
изоэнтальпийным процессом; на самом деле, в узком сечении
энтальпия газа уменьшается, а затем снова восстанавливается.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 31Дросселирование газов
Изменение энтальпии газа:
h1-h2=cp(t1-t2).
Для условно изоэнтальпийного
дросселирования h2=h1, то есть t2=t1. Но это справедливо только для
идеальных газов; реальные газы при
дросселировании меняют свою
температуру (см. hs-диаграмму).
Изменение температуры газа при дросселировании называется
эффектом Джоуля-Томсона.
t1
t2
t3
p1
p2
1
2
3
4
5
6
h
s
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 32Температура инверсии
На предыдущем слайде изображено дросселирование воздуха
при разных
начальных температурах.
При достаточно высокой начальной t1 температура воздуха
при дросселировании 1-2 возрастает.
При некоторой t3 (температуре инверсии) газ ведет себя как
идеальный (t4=t3).
Большинство газов имеют довольно высокую температуру
инверсии (600 °С) и выше. Исключение составляют водород и
гелий (для Н2 температура инверсии -80 °С).
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 33Использование дросселирования
для ожижения газов
Снижение температуры газа при дросселировании,
если
tнач
газ многократно сжимается с охлаждением и последующим дросселированием.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 34Дросселирование (мятие) пара
Если мятию подвергается
перегретый пар 1-2,
то давление
и температура его уменьшаются,
а объем и степень
перегрева возрастают.
При дросселировании 3-4 пар
последовательно переходит в
сухой насыщенный, затем во влажный и снова в перегретый.
Мятие влажного пара 5-6 приводит к росту его степени сухости.
При дросселировании закипающей воды 7-8 она испаряется с
увеличением степени сухости пара.
х=1
р1
р2
р3
р4
h
s
t1
t2
t3
1
2
3
4
5
6
7
8
A
B
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 35Снижение работоспособности
пара при дросселировании
Из диаграммы хорошо видно, что
работоспособность пара
после дросселирования значительно падает (h2-hB)
по возможности надо избегать. Но дроссели применяются в холодильных установках.
Используется также дроссельное регулирование мощности
паровых турбин.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 36Опыт Джоуля-Томсона
В физике дросселирование пара
осуществляют в опыте
Джоуля-Томсона,
пропуская газ или пар через пористую
пластину.
Реальное
мятие пара выглядит в виде зеленой ломаной линии (последовательного дросселирования
от поры к поре при малом перепаде давлений).
При дросселировании получается процесс, аналогичный
истечению: скорость возрастает, затем кинетическая энергия
переходит в тепловую, которая усваивается паром при р=const.
В пределе получается линия 1-2 (изоэнтальпа).
h
s
1
2
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014