Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Точки на прямой
Содержание
- 1. Точки на прямой
- 2. ОтрезокОтрезком называется часть прямой, состоящая из двух
- 3. ЛучДля обозначения лучей используются пары прописных латинских
- 4. Равенство отрезковОдной из основных операций, которую можно
- 5. Сложение отрезковЕсли на отрезке АВ между точками
- 6. Вопрос 1Какое свойство принимается в качестве аксиомы
- 7. Вопрос 2В каком случае говорят, что точка
- 8. Вопрос 3Какая фигура называется отрезком?Ответ: Отрезком называется
- 9. Вопрос 4Как обозначается отрезок?Ответ: Отрезок обозначается указанием его концов.
- 10. Вопрос 5Какая фигура называется лучом?Ответ: Лучом называется
- 11. Вопрос 6Как обозначаются лучи?Ответ: Для обозначения лучей
- 12. Вопрос 7Какое свойство принимается за аксиому откладывания
- 13. Вопрос 8Какие два отрезка называются равными?Ответ: Два
- 14. Вопрос 9Как сложить два отрезка?Ответ: Чтобы сложить
- 15. Вопрос 10Как обозначается сумма отрезков AB и CD?Ответ: АВ + CD.
- 16. Вопрос 11В каком случае говорят, что отрезок
- 17. Вопрос 12Как обозначается то, что отрезок AB меньше отрезка CD?Ответ: АВ < CD.
- 18. Вопрос 13Как из большего отрезка вычесть меньший?
- 19. Упражнение 1Между какими точками лежит точка D
- 20. Упражнение 2Какие точки лежат по одну сторону
- 21. Упражнение 3Для точек A, B, C, D
- 22. Упражнение 4На сколько частей делят прямую:а) одна
- 23. Упражнение 5Назовите отрезки, концами которых являются точки,
- 24. Упражнение 6Для точек A, B прямой укажите,
- 25. Упражнение 7На прямой отмечены точки А, В,
- 26. Упражнение 8Назовите лучи, вершинами которых являются точки,
- 27. Упражнение 9На отрезке АВ взята точка С.
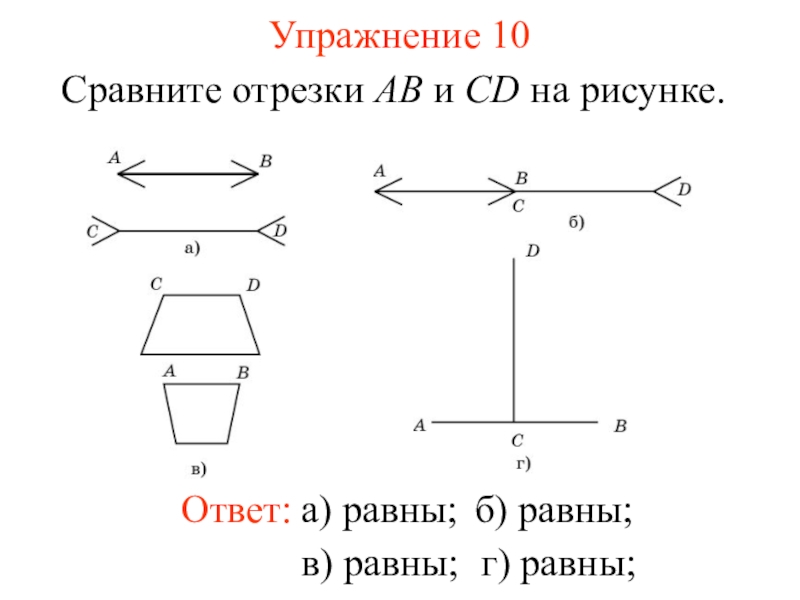
- 28. Упражнение 10Сравните отрезки AB и CD на рисунке. б) равны;в) равны;г) равны;
- 29. Упражнение 11*Можно ли соединить пять точек плоскости
- 30. Скачать презентанцию
ОтрезокОтрезком называется часть прямой, состоящая из двух данных точек и всех точек, лежащих между ними. При этом сами данные точки называются концами отрезка. Отрезок обозначается указанием его концов, например, отрезок с
Слайды и текст этой презентации
Слайд 1Точки на прямой
В качестве аксиомы взаимного расположения точек на прямой
принимается следующее свойство.
разные стороны от точки C, то говорят также, что точка C лежит между точками A и B.
Слайд 2Отрезок
Отрезком называется часть прямой, состоящая из двух данных точек и
всех точек, лежащих между ними. При этом сами данные точки
называются концами отрезка.Отрезок обозначается указанием его концов, например, отрезок с концами A и B обозначается AB.
Слайд 3Луч
Для обозначения лучей используются пары прописных латинских букв, например, AB,
первая из которых обозначает начало луча, а вторая - какую-нибудь
точку, принадлежащую лучу.
Слайд 4Равенство отрезков
Одной из основных операций, которую можно производить с отрезками,
является операция откладывания данного отрезка на данном луче от его
вершины. Получающийся при этом отрезок называется равным исходному отрезку.В качестве аксиомы принимается следующее свойство.
На любом луче от его начала можно отложить только один отрезок, равный данному.
Равенство отрезков АВ и А1В1 записывается в виде АВ = А1В1. Оно означает, что если один из этих отрезков, например АВ, отложить на луче А1В1 от точки А1, то отрезок АВ при этом совместится с отрезком А1В1.
Если при откладывании отрезка АВ на луче А1В1 от точки А1 точка В переходит в точку B', лежащую между точками А1 и В1, то говорят, что отрезок АВ меньше отрезка А1В1 и обозначают АВ < А1В1. Говорят также, что отрезок А1В1 больше отрезка АВ и обозначают А1В1 > AB.
Слайд 5Сложение отрезков
Если на отрезке АВ между точками А и В
взять какую-либо точку С, то образуется два новых отрезка АС
и СВ. Отрезок АВ называется суммой отрезков АС и СВ и обозначается АВ = АС + СВ. Каждый из отрезков АС и СВ называется разностью отрезка АВ и другого отрезка, обозначается АС = АВ - СВ, СВ = АВ - АС.Аналогичным образом поступают для вычитания из большего отрезка меньшего.
Слайд 6Вопрос 1
Какое свойство принимается в качестве аксиомы взаимного расположения точек
на прямой?
Ответ: Каждая точка на прямой разбивает эту прямую на
две части так, что точки из разных частей лежат по разные стороны от данной точки, а точки из одной части лежат по одну сторону от данной точки.
Слайд 7Вопрос 2
В каком случае говорят, что точка C лежит между
точками A и B?
Ответ: Точка C лежит между точками A
и B, если точки A и B лежат по разные стороны от точки C.
Слайд 8Вопрос 3
Какая фигура называется отрезком?
Ответ: Отрезком называется часть прямой, состоящая
из двух данных точек и всех точек, лежащих между ними.
Слайд 10Вопрос 5
Какая фигура называется лучом?
Ответ: Лучом называется часть прямой, состоящая
из данной точки и всех точек, лежащих от нее по
одну сторону.
Слайд 11Вопрос 6
Как обозначаются лучи?
Ответ: Для обозначения лучей используются пары прописных
латинских букв, например, AB, первая из которых обозначает начало луча,
а вторая - какую-нибудь точку, принадлежащую лучу.
Слайд 12Вопрос 7
Какое свойство принимается за аксиому откладывания отрезка?
Ответ: На любом
луче от его начала можно отложить только один отрезок, равный
данному.
Слайд 13Вопрос 8
Какие два отрезка называются равными?
Ответ: Два отрезка называются равными,
если один получается из другого операцией откладывания отрезка.
Слайд 14Вопрос 9
Как сложить два отрезка?
Ответ: Чтобы сложить два отрезка АВ
и CD, продолжим отрезок АВ за точку В и на
этом продолжении отложим отрезок ВЕ, равный отрезку CD. Отрезок АЕ даст сумму отрезков АВ и CD
Слайд 16Вопрос 11
В каком случае говорят, что отрезок АВ меньше отрезка
А1В1?
Ответ: Если при откладывании отрезка АВ на луче А1В1 от
точки А1 точка В переходит в точку B', лежащую между точками А1 и В1, то говорят, что отрезок АВ меньше отрезка А1В1. 
Слайд 19Упражнение 1
Между какими точками лежит точка D на рисунке?
Ответ:
E и F, C и F, A и F, O
и F, B и F.
Слайд 20Упражнение 2
Какие точки лежат по одну сторону от точки A
на рисунке?
Ответ: E и C; O, B, D и F.
Слайд 21Упражнение 3
Для точек A, B, C, D прямой известно, что
точки В и С лежат по одну сторону от точки
А, точки В и D тоже лежат по одну сторону от точки А. Как расположены точки С и D относительно точки А?
Слайд 22Упражнение 4
На сколько частей делят прямую:
а) одна точка?
б) две точки?
две;
три;
в) три точки?
четыре;
г)* n точек?
n + 1.
Слайд 23Упражнение 5
Назовите отрезки, концами которых являются точки, изображенные на рисунках:
а), б).
Ответ: а) AB, AC, BC;
б) AB, AC, AD,
BC, BD, CD. 
Слайд 24Упражнение 6
Для точек A, B прямой укажите, где расположены точки
C, для которых выполняются равенства:
а) AC +
BC = AB; б) AC – BC = AB; в) BC – AC = AB.б) точки, лежащие от B по другую сторону, чем точка A;
в) точки, лежащие от A по другую сторону, чем точка B.
Слайд 25Упражнение 7
На прямой отмечены точки А, В, С, D. Выразите
каждый из отрезков в виде суммы или разности остальных.
Ответ: AB
= AC – BC; AC = AB + BC; AD = AB + BC + CD; BC = BD – CD; BD = BC + CD; CD = BD – BC.
Слайд 26Упражнение 8
Назовите лучи, вершинами которых являются точки, изображенные на рисунках.
Ответ:
а) EA, EB, FA, FB, GA, GB;
б) KC, KD,
LC, LD, MC, MD, NC, ND. 
Слайд 27Упражнение 9
На отрезке АВ взята точка С. Среди лучей АВ,
АС, СА, СВ, BA, BC назовите пары совпадающих лучей.
Ответ: CA
и CB.
Слайд 29Упражнение 11*
Можно ли соединить пять точек плоскости отрезками так, чтобы
каждая точка была соединена ровно с:
а) двумя; б) тремя;
в) четырьмя другими? б) нет;
в) да.
