Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Транспортные задачи
Содержание
- 1. Транспортные задачи
- 2. Под названием транспортная задача объединяется широкий круг задач с единой математической моделью.
- 3. Транспортная задача (задача Монжа — Канторовича) —
- 4. Для простоты понимания рассматривается как задача об
- 5. Слайд 5
- 6. Транспортная задача (классическая) — задача об оптимальном
- 7. Слайд 7
- 8. Исторический поиск методы решения Проблема была впервые
- 9. Гаспар Монж(Французский математик, геометр, государственный деятель, морской
- 10. Методы решенияКлассическую транспортную задачу можно решить симплекс-методом,
- 11. Метод северо-западного угла (диагональный или
- 12. Метод наименьшего элемента.Одним из способов решения задачи
- 13. Слайд 13
- 14. Слайд 14
- 15. Скачать презентанцию
Под названием транспортная задача объединяется широкий круг задач с единой математической моделью.
Слайды и текст этой презентации
Слайд 1Транспортные задачи
Выполнил студент
Группы БрОП-311
Новикова Ангелина
Проверил преподаватель
Цыганкова
З.С.
Слайд 2Под названием транспортная задача объединяется широкий круг задач с единой
математической моделью.
Слайд 3Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного
программирования специального вида о поиске оптимального распределения однородных объектов из
аккумулятора к приемникам с минимизацией затрат на перемещение.Слайд 4Для простоты понимания рассматривается как задача об оптимальном плане перевозок
грузов из пунктов отправления в пункты потребления, с минимальными затратами
на перевозки. Транспортная задача по теории сложности вычислений входит в класс сложности P. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).Слайд 6Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного
продукта из однородных пунктов наличия в однородные пункты потребления на
однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачиСлайд 8Исторический поиск методы решения
Проблема была впервые формализована французским математиком
Гаспаром Монжем в 1781 году. Прогресс в решении проблемы был
достигнут во время Великой Отечественной войны советским математиком и экономистом Леонидом Канторовичем. Поэтому иногда эта проблема называется транспортной задачей Монжа — Канторовича.Слайд 9Гаспар Монж
(Французский математик, геометр, государственный деятель, морской министр)
Канторович Леонид Витальевич
(Советский
математик и экономист, пионер и один из создателей линейного программирования.)
Слайд 10Методы решения
Классическую транспортную задачу можно решить симплекс-методом, но в силу
ряда особенностей её можно решить проще (для задач малой размерности).
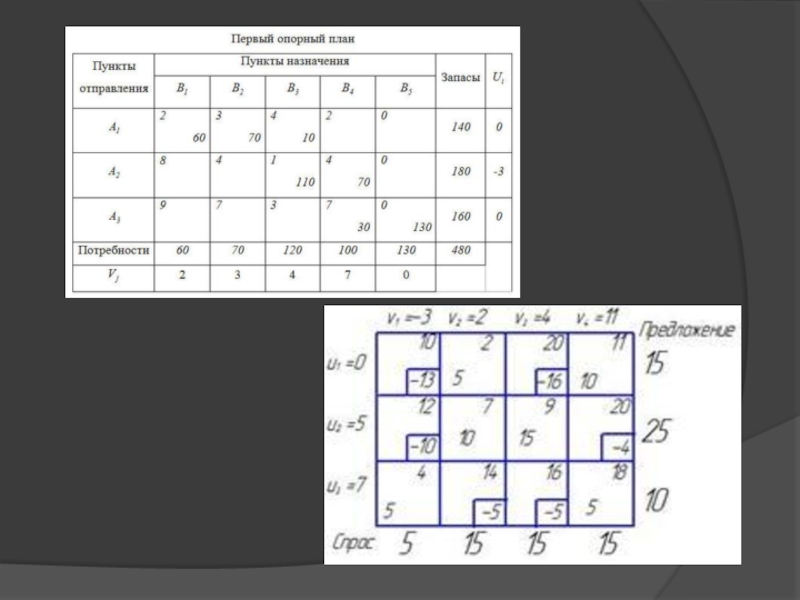
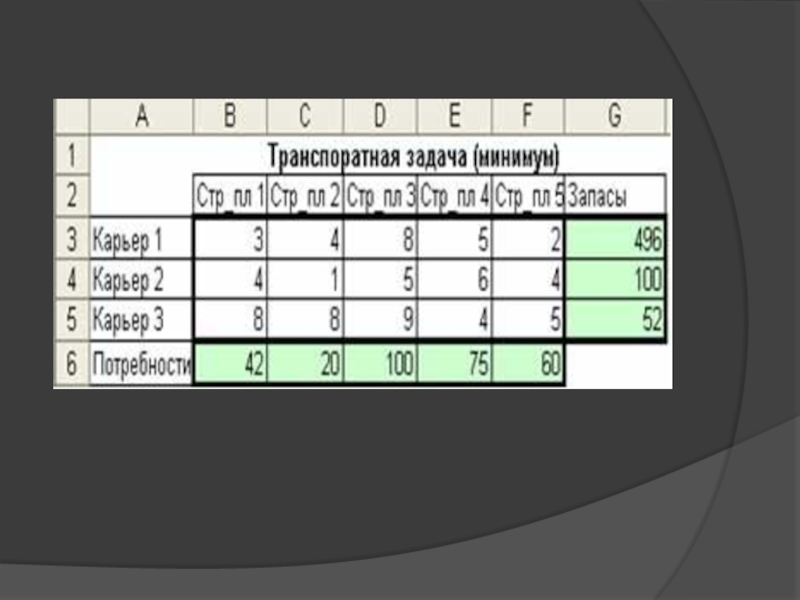
Условия
задачи располагают в таблице, вписывая в ячейки количество перевозимого груза из ~A_i в ~B_j груза ~X_ij больше либо равно 0, а в маленькие клетки — соответствующие тарифы ~C_ij.Требуется определить опорный план и путём последовательных операций найти оптимальное решение. Опорный план можно найти следующими методами: «северо-западного угла», «наименьшего элемента», двойного предпочтения и аппроксимации Фогеля.
Слайд 11 Метод северо-западного угла (диагональный или улучшенный)
На каждом этапе
максимально возможным числом заполняют левую верхнюю клетку оставшейся части таблицы.
Заполнение таким образом, что полностью выносится груз из ~A_i или полностью удовлетворяется потребность ~B_jСлайд 12Метод наименьшего элемента.
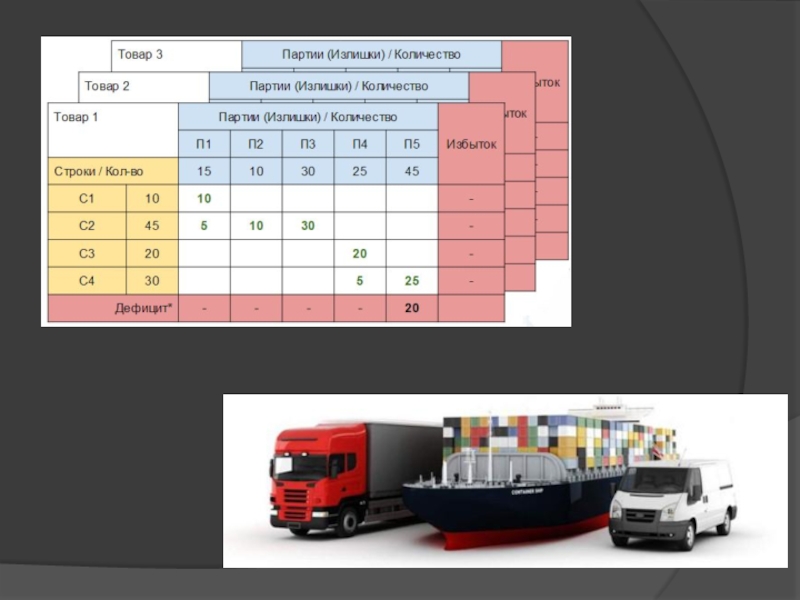
Одним из способов решения задачи является метод минимального
(наименьшего) элемента. Его суть заключается в сведении к минимуму побочных
перераспределений товаров между потребителями.Алгоритм:
1.Из таблицы стоимостей выбирают наименьшую стоимость и в клетку, которая ей соответствует, вписывают большее из чисел.
2.Проверяются строки поставщиков на наличие строки с израсходованными запасами и столбцы потребителей на наличие столбца, потребности которого полностью удовлетворены. Такие столбцы и строки далее не рассматриваются.
3.Если не все потребители удовлетворены и не все поставщики израсходовали товары, возврат к п. 1, в противном случае задача решена.