Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тренировочная работа №2 Расстояние от точки до плоскости
Содержание
- 1. Тренировочная работа №2 Расстояние от точки до плоскости
- 2. Повторение:АРасстояние от точки до плоскости, не содержащей
- 3. Повторение:Если прямая параллельна плоскости, то все точки
- 4. Повторение:Если две плоскости параллельны, то все точки
- 5. Повторение:1) Равно расстоянию до плоскости от
- 6. DАВСD1С1Подсказка В1А1Найдите расстояние от вершины куба до
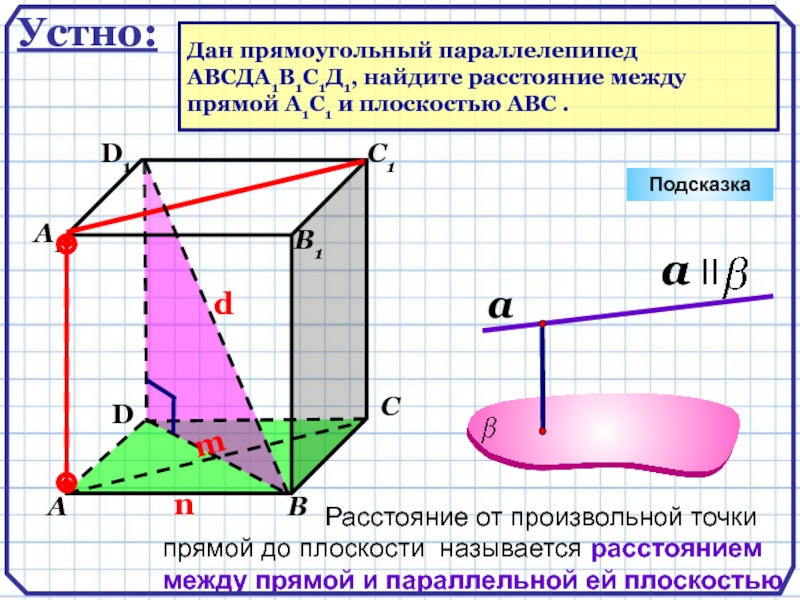
- 7. DАВСА1D1С1В1Подсказка Устно:Дан прямоугольный параллелепипед ABCДA1B1C1Д1, найдите расстояние между прямой А1С1 и плоскостью АВС .
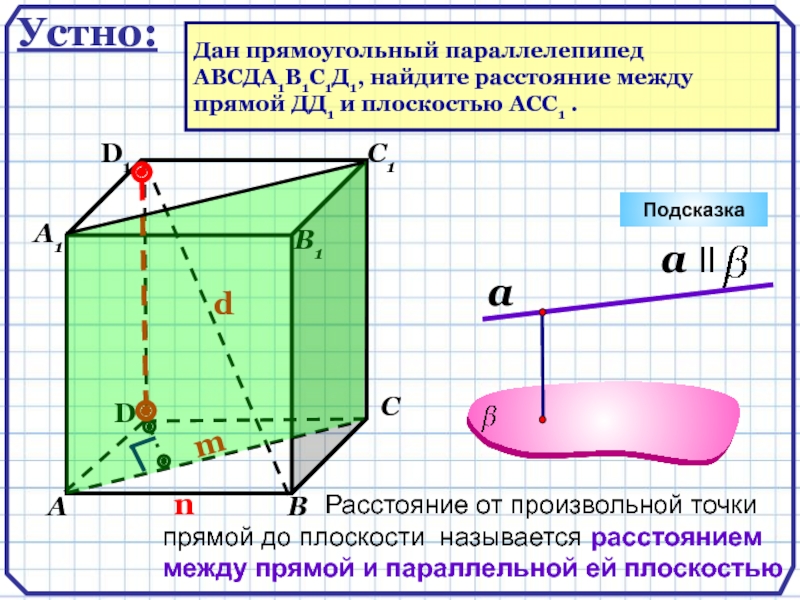
- 8. DАВСА1D1С1Подсказка В1Устно:Дан прямоугольный параллелепипед ABCДA1B1C1Д1, найдите расстояние между прямой ДД1 и плоскостью АСС1 .
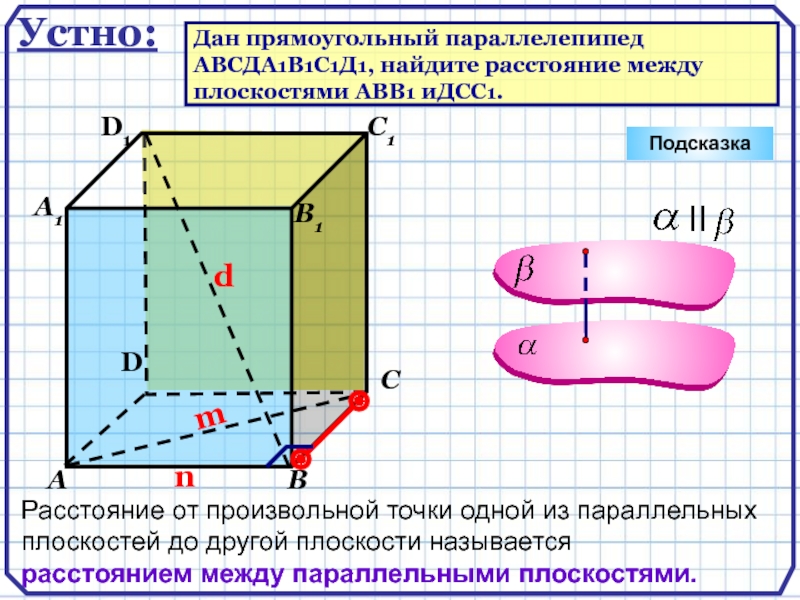
- 9. DАВСА1D1С1В1Подсказка Устно:Дан прямоугольный параллелепипед ABCДA1B1C1Д1, найдите расстояние между плоскостями АВВ1 иДСС1.
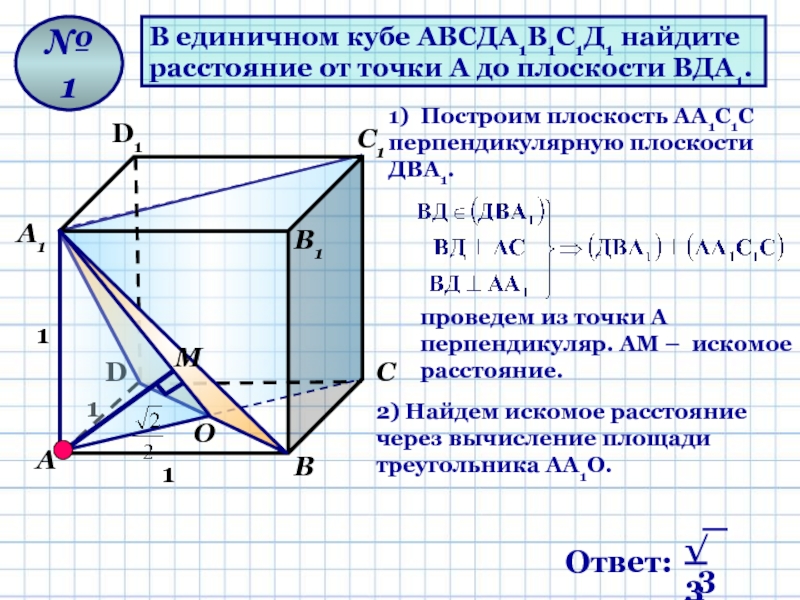
- 10. В единичном кубе АВСДА1В1С1Д1 найдите расстояние от
- 11. Критерии оценивания выполнения задания С2
- 12. В единичном кубе АВСДА1В1С1Д1 найдите расстояние от
- 13. В единичном кубе АВСДА1В1С1Д1 найдите расстояние от
- 14. В правильной шестиугольной пирамиде SАВСDЕF, стороны основания
- 15. В правильной шестиугольной призме А…..F1, все ребра
- 16. В правильной треугольной призме АВСА1В1С1 Все ребра
- 17. 1. В.А. Смирнов ЕГЭ 2011. Математика. Задача
- 18. Скачать презентанцию
Повторение:АРасстояние от точки до плоскости, не содержащей эту точку, есть длина перпендикуляра, проведенного из этой точки на данную плоскость.Н
Слайды и текст этой презентации
Слайд 2
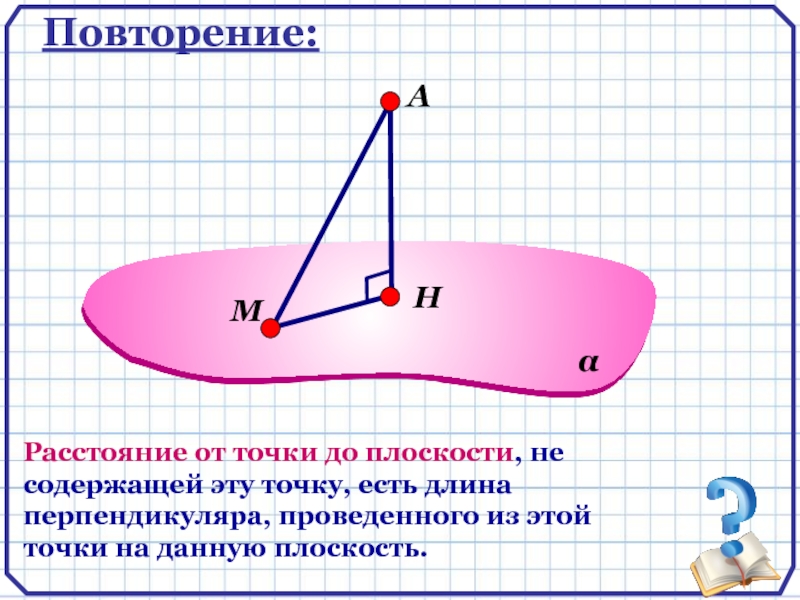
Повторение:
А
Расстояние от точки до плоскости, не содержащей эту точку, есть
длина перпендикуляра, проведенного из этой точки на данную плоскость.
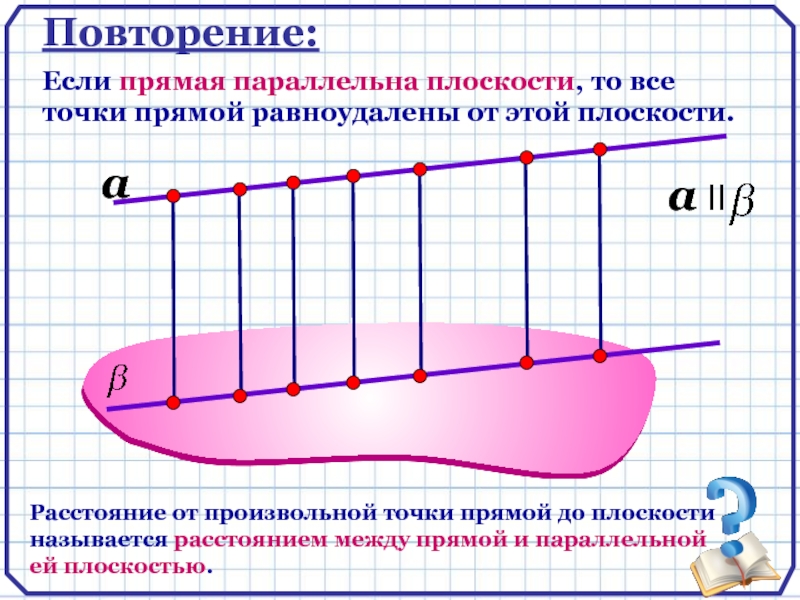
Слайд 3Повторение:
Если прямая параллельна плоскости, то все точки прямой равноудалены от
этой плоскости.
Расстояние от произвольной точки прямой до плоскости называется расстоянием
между прямой и параллельной ей плоскостью.a
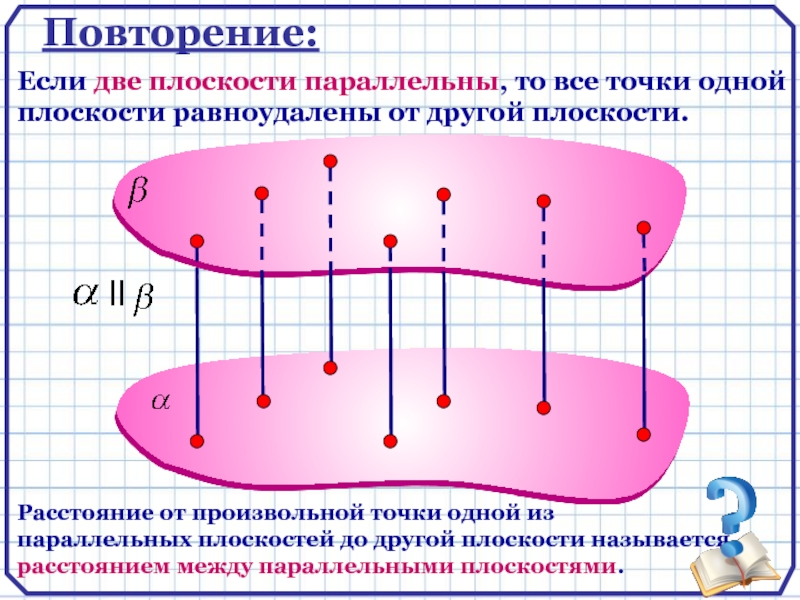
Слайд 4Повторение:
Если две плоскости параллельны, то все точки одной плоскости равноудалены
от другой плоскости.
Расстояние от произвольной точки одной из параллельных плоскостей
до другой плоскости называется расстоянием между параллельными плоскостями.
Слайд 5Повторение:
1) Равно расстоянию до плоскости от произвольной точки Р,
лежащей на прямой а, которая проходит ч/з точку М и
параллельна плоскости ;Расстояние от точки М до плоскости :
2) Равно расстоянию до плоскости от произвольной точки Р, лежащей на плоскости , которая проходит ч/з точку М и параллельна плоскости ;
3) Находится с помощью координатно – векторного метода;
Слайд 6D
А
В
С
D1
С1
Подсказка
В1
А1
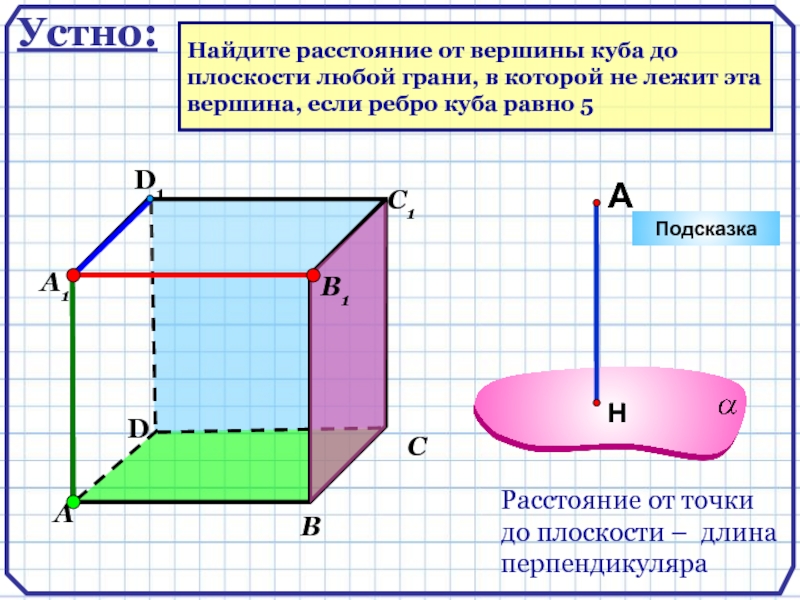
Найдите расстояние от вершины куба до
плоскости любой грани,
в которой не лежит эта
вершина, если ребро куба равно
5Устно:
Слайд 7D
А
В
С
А1
D1
С1
В1
Подсказка
Устно:
Дан прямоугольный параллелепипед
ABCДA1B1C1Д1, найдите расстояние между
прямой А1С1
и плоскостью АВС .
Слайд 8D
А
В
С
А1
D1
С1
Подсказка
В1
Устно:
Дан прямоугольный параллелепипед
ABCДA1B1C1Д1, найдите расстояние между
прямой ДД1
и плоскостью АСС1 .
Слайд 9D
А
В
С
А1
D1
С1
В1
Подсказка
Устно:
Дан прямоугольный параллелепипед
ABCДA1B1C1Д1, найдите расстояние между
плоскостями АВВ1
иДСС1.
Слайд 10В единичном кубе АВСДА1В1С1Д1 найдите
расстояние от точки А до
плоскости ВДА1.
№ 1
1
1
1
О
М
1) Построим плоскость AА1С1С перпендикулярную плоскости ДВА1.
проведем из
точки А перпендикуляр. АМ – искомое расстояние.2) Найдем искомое расстояние через вычисление площади треугольника AА1О.
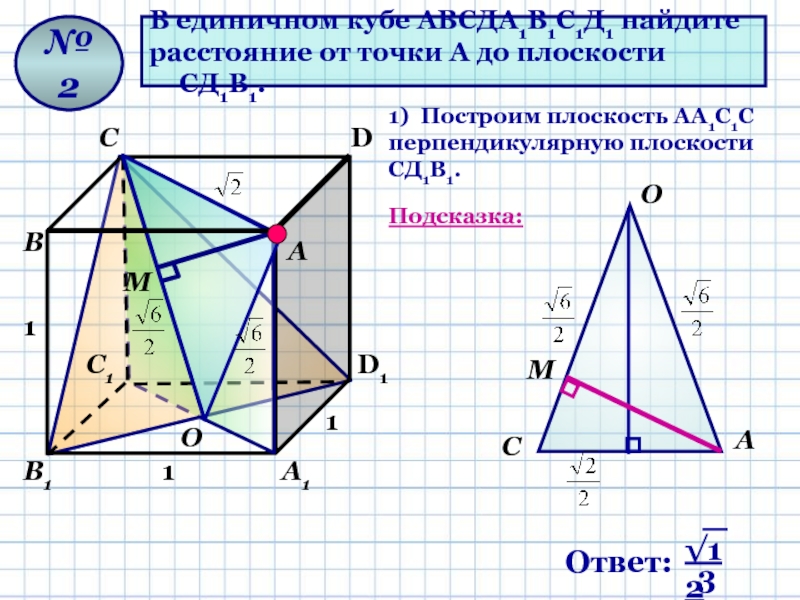
Слайд 12В единичном кубе АВСДА1В1С1Д1 найдите
расстояние от точки А до
плоскости СД1В1.
№ 2
1
1
1
М
О
1) Построим плоскость AА1С1С перпендикулярную плоскости СД1В1.
Подсказка:
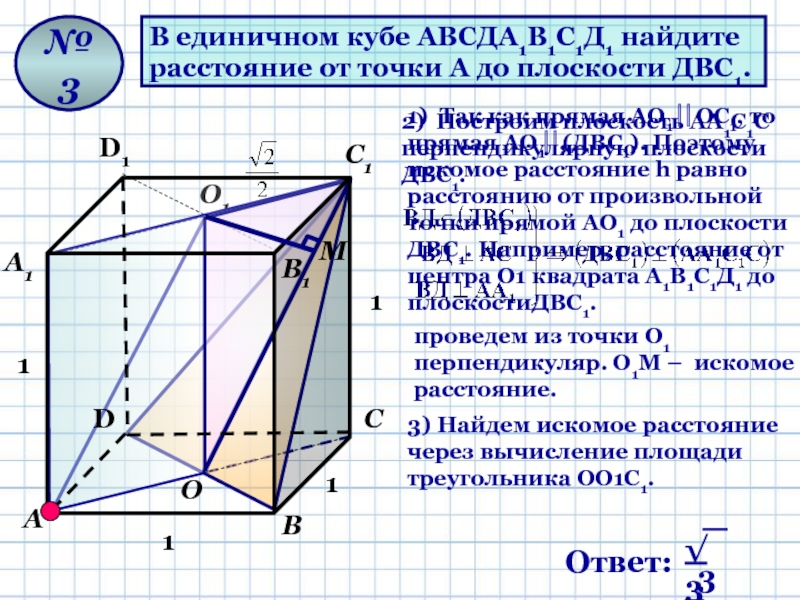
Слайд 13В единичном кубе АВСДА1В1С1Д1 найдите
расстояние от точки А до
плоскости ДВС1.
№ 3
1
1
1
1
М
1) Так как прямая АО1 ОС1, то прямая
АО1(ДВС1). Поэтому искомое расстояние h равно расстоянию от произвольной точки прямой АО1 до плоскости ДВС1. Например, расстояние от центра О1 квадрата А1В1С1Д1 до плоскостиДВС1.3) Найдем искомое расстояние через вычисление площади треугольника ОО1С1.
О
О1
2) Построим плоскость AА1С1С перпендикулярную плоскости ДВС1.
проведем из точки О1 перпендикуляр. О1М – искомое расстояние.
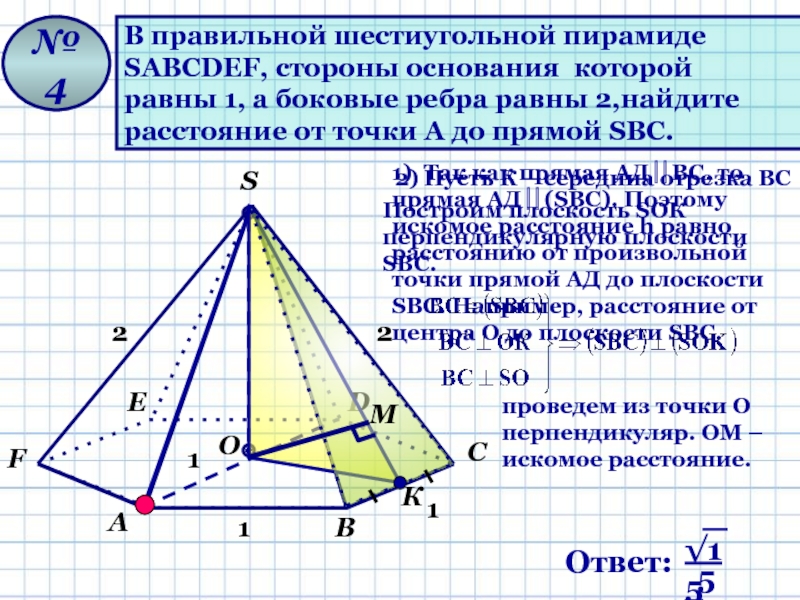
Слайд 14В правильной шестиугольной пирамиде
SАВСDЕF, стороны основания которой
равны 1,
а боковые ребра равны 2,найдите
расстояние от точки А до
прямой SВС.№ 4
1
1
1
2
2
2) Пусть К – середина отрезка ВС
О
М
1) Так как прямая АД ВС, то прямая АД (SВС). Поэтому искомое расстояние h равно расстоянию от произвольной точки прямой АД до плоскости SВС. Например, расстояние от центра О до плоскости SВС.
Построим плоскость SОК перпендикулярную плоскости SВС.
проведем из точки О перпендикуляр. ОМ – искомое расстояние.
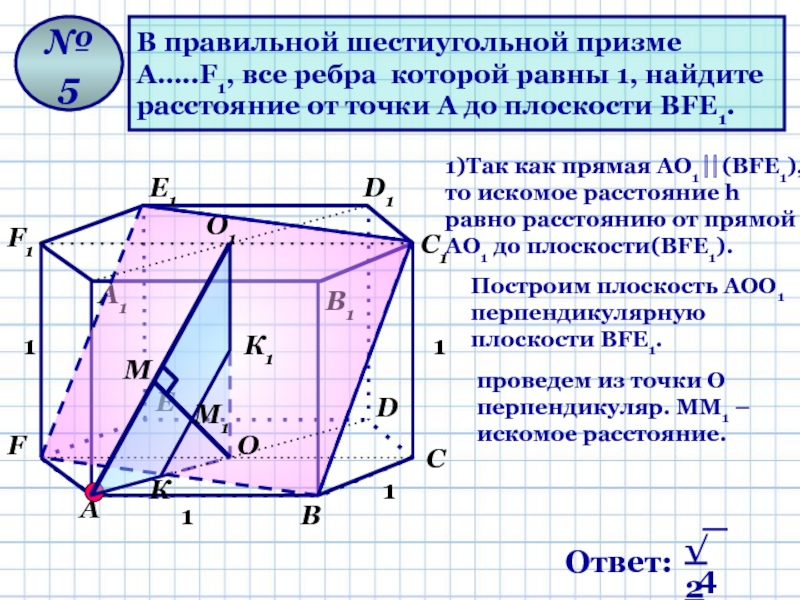
Слайд 15В правильной шестиугольной призме
А…..F1, все ребра которой равны 1,
найдите
расстояние от точки А до плоскости ВFЕ1.
№ 5
1
1
1
1
О
О1
М
К
К1
1)Так как
прямая АО1 (ВFЕ1), то искомое расстояние h равно расстоянию от прямой АО1 до плоскости(ВFЕ1). Построим плоскость АОО1 перпендикулярную плоскости ВFЕ1.
М1
проведем из точки О перпендикуляр. ММ1 – искомое расстояние.
Слайд 16В правильной треугольной призме АВСА1В1С1
Все ребра которой равны 1,
найдите
расстояние от точки А до плоскости:
а) ВСА1; б)
СА1В1Домашнее задание
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1, найдите
расстояние от точки А до плоскости SСД.
Слайд 171. В.А. Смирнов ЕГЭ 2011. Математика. Задача С2. Геометрия. Стереометрия.
/ Под. редакцией А.Л. Семенова и И.В. Ященко. – М.:
МЦНМО, 2011.2. http://le-savchen.ucoz.ru/
Литература
