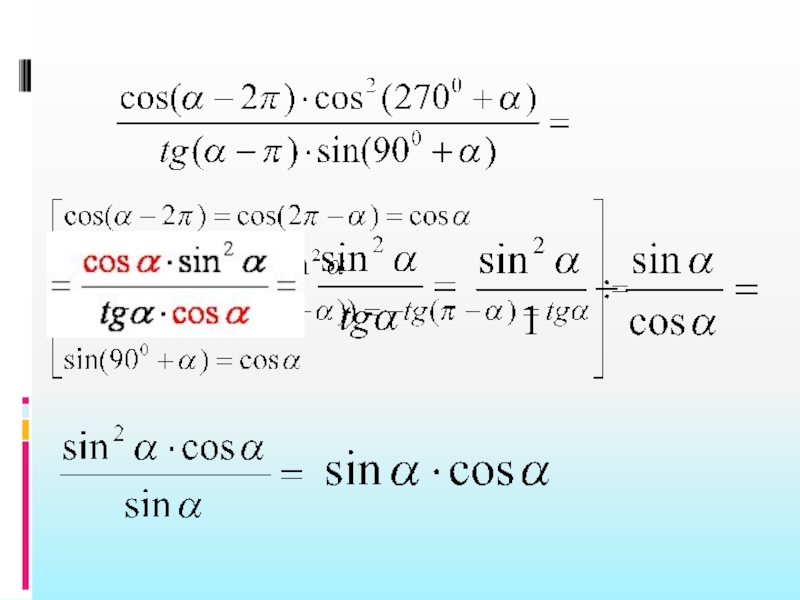выражения и составления плана действий. Иногда могут быть полезны следующие
рекомендации:1.Если выражение содержит разные тригонометрические функции одного аргумента, то попробуйте все функции выразить через одну или две функции. При этом тангенс и котангенс угла чаще всего выражают через синус и косинус этого же угла;
2.Если в выражение входят тригонометрические функции от разных аргументов, то попытайтесь свести все функции к одному аргументу;
3.Формулы приведения могут быть полезны для выражения тригонометрической функции через кофункцию;